Odisha State Board BSE Odisha 10th Class Physical Science Solutions Chapter 6 ଆଲୋକ- ପ୍ରତିଫଳନ ଓ ପ୍ରତିସରଣ Textbook Exercise Questions and Answers.
BSE Odisha Class 10 Physical Science Solutions Chapter 6 ଆଲୋକ- ପ୍ରତିଫଳନ ଓ ପ୍ରତିସରଣ
Question 1.
ନିମ୍ନଲିଖତ ପଦାର୍ଥ ଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁ ଗୋଟିକ ଲେନ୍ସ ତିଆରିରେ ବ୍ୟବହୃତ ହୋଇପାରିବ ନାହିଁ ?
(a) ଜଳ
(b) କାର
(c) ପ୍ଲାଷ୍ଟିକ
(d) ମାଟି
Answer:
(d) ମାଟି (କାରଣ ମାଟି ଅସ୍ବଚ୍ଛ ଅଟେ)
Question 2.
ଗୋଟିଏ ଅବତଳ ଦର୍ପଣରେ ସୃଷ୍ଟ ପ୍ରତିବିମ୍ବ ଆଭାସୀ, ସଳଖ ଓ ବସ୍ତୁଠାରୁ ଆକାରରେ ବଡ଼ । ତାହା ହେଲେ
(a) ପ୍ରମୁଖ ଫୋକସ୍ ଓ ବକ୍ରତା କେନ୍ଦ୍ର ମଧ୍ୟରେ
(b) ବକ୍ରତା କେନ୍ଦ୍ର ଉପରେ
(c) ବକ୍ରତା କେନ୍ଦ୍ରଠାରୁ ଦୂରରେ
(d) ଦର୍ପଣର ପୋଲ୍ ଓ ପ୍ରମୁଖ ଫୋକସ୍ ମଧ୍ୟରେ
Answer:
(d) ଦର୍ପଣର ପୋଲ୍ ଓ ପ୍ରମୁଖ ଫୋକସ୍ ମଧ୍ୟରେ
Question 3.
ଗୋଟିଏ ଉତ୍ତଳ ଲେନ୍ସ ସମ୍ମୁଖରେ ବସ୍ତୁ କେଉଁଠି ରହିଲେ ସମାନ ଆକାରର ବାସ୍ତବ ପ୍ରତିବିମ୍ବ ମିଳିପାରିବ ?
(a) ଲେନ୍ସର ପ୍ରମୁଖ ଫୋକସ୍ ଠାରେ
(b) ଫୋକସ୍ ଦୂରତାର ଦୁଇଗୁଣ ଦୂରତ୍ଵରେ
(c) ଅନନ୍ତ୍ର ତ୍ରରତାରେ
(d) ଲେନ୍ସର ଆଲୋକ କେନ୍ଦ୍ର ଓ ପ୍ରମୁଖ ଫୋକସ୍ ମଧ୍ୟରେ
Answer:
(b) ଫୋକସ୍ ଦୂରତାର ଦୁଇଗୁଣ ଦୂରତ୍ୱରେ
Question 4.
ଗୋଟିଏ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣ ଓ ବର୍ତ୍ତୁଳାକାର ଲେନ୍ସ ପ୍ରତ୍ୟେକର ଫୋକସ୍ ଦୂରତା 15 ସେ.ମି. ଅଟେ । ଦର୍ପଣ ଓ ଲେନ୍ସ ଦ୍ବୟ ସମ୍ଭବତଃ କ’ଣ ହୋଇପାରିବେ ?
(a) ଉଭୟ ଅବତଳ
(b) ଉଭୟ ଉତ୍ତଳ
(c) ଦର୍ପଣ ଅବତଳ ଓ ଲେନ୍ସ ଉତ୍ତଳ
(d) ଦର୍ପଣ ଉତ୍ତଳ ଓ ଲେନ୍ସ ଅବତଳ
Answer:
(a) ଉଭୟ ଅବତଳ
![]()
Question 5.
ତୁମେ ଗୋଟିଏ ଦର୍ପଣ ସମ୍ମୁଖରେ ଯେଉଁଠି ଠିଆ ହେଲେ ବି ତୁମର ପ୍ରତିବିମ୍ବ ସଳଖ ହୁଏ । ତେବେ ଦର୍ପଣ କି ପ୍ରକାର ଦର୍ପଣ ହେବାର ସମ୍ଭାବନା ଅଛି ?
(a) ସମତଳ
(b) ଅବ୍ତଳ
(c) ଉତ୍ତଳ
(d) ସମତଳ କିମ୍ବା ଉତ୍ତଳ
Answer:
(d) ସମତଳ କିମ୍ବା ଉତ୍ତଳ
[ କାରଣ ସମତଳ ଦର୍ପଣରେ ସର୍ବଦା ସଳଖ ପ୍ରତିବିମ୍ବ ଦେଖାଯାଏ । ଉତ୍ତଳ ଦର୍ପଣରେ ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ସର୍ବଦା ଆଭାସୀ ଓ ସଳଖ ହୋଇଥାଏ ।]
Question 6.
ଡିକ୍ସନାରିର ଛୋଟ ଛୋଟ ଅକ୍ଷର ପଢ଼ିବା ପାଇଁ ତୁମେ ନିମ୍ନଲିଖ୍ ଲେନ୍ସଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁ ଲେନ୍ସକୁ ବ୍ୟବହାର କରିବା ପାଇଁ ବାଛିବ ?
(a) 50 ସେମି ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଉତ୍ତଳ ଲେନ୍ସସ।
(b) 50 ସେମି ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଅବତଳ ଲେନ୍ସସ ।
(c) 5 ସେମି ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଉତ୍ତଳ ଲେନ୍ସସ।
(d) 5 ସେମି ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଅବତଳ ଲେନ୍ସସ ।
Answer:
(c) 5 ସେମି ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଉତ୍ତଳ ଲେନ୍ସସ।
Question 7.
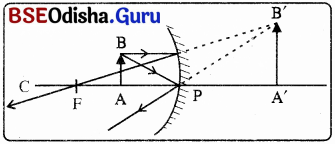
15 ସେମି ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଅବତଳ ଦର୍ପଣ ବ୍ୟବହାର କରି ଆମେ ଗୋଟିଏ ବସ୍ତୁର ସଳଖ ପ୍ରତିବିମ୍ବ ପାଇବାକୁ ଇଚ୍ଛା କରୁଛୁ । ଦର୍ପଣ ସମ୍ମୁଖରେ ବସ୍ତୁ କେଉଁ ଦୂରତା ପରିସର (Range) ମଧ୍ୟରେ ରହିବ ? ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି କ’ଣ ? ପ୍ରତିବିମ୍ବର ଆକାର ବସ୍ତୁଠାରୁ ବଡ଼ ନା ସାନ ? ରଶ୍ମି ଚିତ୍ର ଅଙ୍କନ କରି ପ୍ରତିବିମ୍ବ ଗଠନ ଦେଖାଅ ।
Answer:
(i) ଅବତଳ ଦର୍ପଣର ପୋଲ୍ ଓ ଫୋକସ୍ ମଧ୍ୟରେ ବସ୍ତୁ ରହିଲେ ଏହାର ଏକ ସଳଖ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହୁଏ ।
(ii) ପ୍ରତିବିମ୍ବ ସଳଖ ଓ ଆଭାସୀ ହୋଇଥାଏ ଏବଂ ଏହା ଦର୍ପଣ ପଛପଟେ ଗଠିତ ହୋଇଥାଏ ।
(iii) ପ୍ରତିବିମ୍ବର ଆକାର ବସ୍ତୁର ଅକାରଠାରୁ ବଡ଼ ହୋଇଥାଏ ।
Question 8.
ନିମ୍ନଲିଖତ କ୍ଷେତ୍ରରେ କି ପ୍ରକାରର ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ ?
(a) କାରର ହେଡ୍ଲାଇଟ :
ଉ :
କାର୍ ହେଡ୍ଲାଇଟ୍ର ପ୍ରତିଫଳକ ରୂପେ ଅବତଳ ଦର୍ପଣକୁ ବ୍ୟବହାର କରାଯାଏ । ଯେତେବେଳେ ଆଲୋକିତ ବଲ୍ବଟ୍
ଅବତଳ ପ୍ରତିଫଳକର ଫୋକସ୍ଠାରେ ରହେ, ଅବତଳ ପ୍ରତିଫଳକ ଶକ୍ତିଶାଳୀ ସମାନ୍ତର ଆଲୋକ ରଶ୍ମିର ଗୁଚ୍ଛ ସୃଷ୍ଟି
କରେ, ଯାହା ଅଧିକ ଦୂର ପର୍ଯ୍ୟନ୍ତ ପଡ଼ିଥାଏ । ଆଲୋକ ରଶ୍ମିର ଗୁଚ୍ଛଗୁଡ଼ିକ ଅଧିକ ଉଜ୍ଜ୍ଵଳ ହୋଇଥାଏ ।
(b) ଯାନର ପଛ ଦେଖିର| ଦର୍ପଣ
ଉ :
ଯାନର ପଛ ଦେଖିବା ପାଇଁ ଉତ୍ତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ । କାରଣ ଉତ୍ତଳ ଦର୍ପଣ ସର୍ବଦା ସଳଖ, ଆଭାସୀ ଓ ଛୋଟ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି କରେ । ଯାନର ପଛପଟେ ଥିବା ବିସ୍ତୀର୍ଣ୍ଣ ଅଞ୍ଚଳର ଦୃଶ୍ୟ ଦର୍ପଣରେ ପରିଷ୍କାର ଭାବେ ଦେଖ୍ହୁଏ ।
(c) ସୌର ଚୁଲ୍ଲା :
ଉ :
ସୌର ଚୁଲାରେ ବଡ଼ ଅବତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ । କାରଣ ଯେତେବେଳେ ସୌରଚୁଲାକୁ ଏକ ବଡ଼ ଅଚ୍ତଳ ପ୍ରତିଫଳକର ଫୋକସ୍ଠାରେ ରଖାଯାଏ, ପ୍ରତିଫଳନଦ୍ୱାରା ସୌର ତାପଯୁକ୍ତ ରଶ୍ମି ଅଭିସରିତ ହୋଇ ଚୁଲା ଉପରେ ଫୋକସ୍ ହୋଇଥାଏ । ଫଳରେ ସୌର ବୁର୍ଲାରେ ତାପ ସୃଷ୍ଟି କରିଥାଏ ।
![]()
Question 9.
ଗୋଟିଏ ଉତ୍ତଳ ଲେନ୍ସର ଅଧା ଅଂଶ କାଗଜ ଦ୍ବାରା ଆବୃତ କରି ଦିଆଯାଇଛି । ଏହି ଲେନ୍ସ ବସ୍ତୁର ସମ୍ପୂର୍ଣ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି କରିପାରିବ କି ? ପରୀକ୍ଷା ଦ୍ବାରା ତୁମ ଉତ୍ତରର ସଠିକତାକ୍ତ ଜାଣିଚ୍|କ୍ତ ଚେଷ୍ଟାକର । ତୁମର ପର୍ଯ୍ୟବେକ୍ଷଣକୁ ବୁଝାଅ ।
Answer:
ଲେନ୍ସ୍ର ପ୍ରତ୍ୟେକ ଅଂଶ ପ୍ରତିବିମ୍ବ ଗଠନ କରେ, ତେଣୁ ଗୋଟିଏ ଉତ୍ତଳ ଲେନ୍ସର ଅଧା ଅଂଶ କାଗଜଦ୍ବାରା ଆବୃତ କଲେ ମଧ୍ୟ ଲେନ୍ସ ବସ୍ତୁର ସମ୍ପୂର୍ଣ୍ଣ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି କରିପାରିବ ।
ପରୀକ୍ଷଣ :
ଗୋଟିଏ ଉତ୍ତଳ ଲେନସ୍ ନିଆଯାଉ । ଏହାର ଅଧା ଅଂଶ କଳାକାଗଜରେ ଆବୃତ୍ତ କରାଯାଉ । ଏକ ବସ୍ତୁ AB ଲେନସ୍ ଆଗରେ ରଖାଯାଉ । ଲେନସ୍ ଏବଂ ବସ୍ତୁଟିକୁ ଏପରି ରଖ ଯେପରିକି ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ଏକ ପରଦା ଉପରେ ପଡ଼ିବ ।
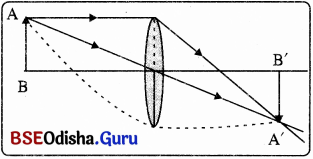
ପର୍ଯ୍ୟବେକ୍ଷଣ :
ପରଦାରେ ବସ୍ତୁର ସମ୍ପୂର୍ଣ୍ଣ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହେବ ।
Question 10.
ଗୋଟିଏ 10 ସେମି ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଅଭିସାରୀ ଲେନ୍ସଠାରୁ 25 ସେମି ଦୂରରେ ଏକ 5 ସେମି ଦୈର୍ଘ୍ୟର ବସ୍ତୁ ରହିଛି । ରଶ୍ମି ଚିତ୍ର ଅଙ୍କନ କରି ପ୍ରତିବିମ୍ବର ସ୍ଥିତି, ପ୍ରକୃତି ଓ ଆକାର ନିର୍ଣ୍ଣୟ କର ।
Answer:
h = 5 ସ୍.ମି., u = – 25 ସ୍.ମି, ƒ = 10 6ସ୍.ମି. |
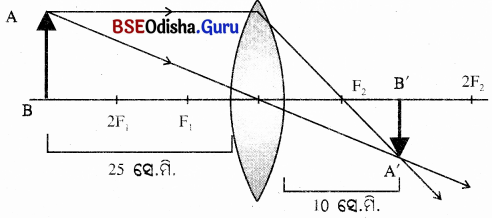
ଯେହେତୁ ବସ୍ତୁଟି ଅପିସାରୀ ଲେନ୍ସଠାରୁ 25 ସେ.ମି. ଦୂରରେ ରହିଛି ଏବଂ ଫୋକସ୍ ଦୂରତା ହେଉଛି 10 ସେ.ମି. ତେଣୁ ବସ୍ତୁଟି 2Fର ବାହାରେ ରହିବ । 10 ସେ.ମି. ତେଣୁ ବସ୍ତୁଟି 2Fର ବାହାରେ ରହିବ ।
ଲେନ୍ସ ସୂତ୍ର ଅନୁଯାୟୀ, \(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\) ⇒ \(\frac { 1 }{ v }\) – \(\frac { 1 }{ -25 }\) = \(\frac { 1 }{ 10 }\)
\(\frac { 1 }{ v }\) = \(\frac { 1 }{ 10 }\) – \(\frac { 1 }{ 25 }\) = \(\frac { 5-2 }{ 50 }\) = \(\frac { 3 }{ 50 }\) ⇒ v = \(\frac { 50 }{ 3 }\) = 16.66 6ସ୍.ମି.
∴ ପ୍ରତିବିମ୍ବର ଦୂରତା 16.66 ସେ.ମି. ।
ବର୍ଦ୍ଧନ (m) = \(\frac { h’ }{ h }\) = \(\frac { v }{ u }\) ⇒ v = \(\frac { h’ }{ 5 }\) = \(\frac{\frac{50}{3}}{-25}\)
⇒ \(\frac { h’ }{ 5 }\) = \(\frac{50}{-3 \times 25}\)
⇒ h’ = \(\frac{50 \times 5}{-3 \times 25}\) = – 3. 33 6ସ୍.ମି.
∴ ପ୍ରତିବିମ୍ବ ଲେନ୍ସର ଅପରପାର୍ଶ୍ବରେ F ଓ 2F ମଧ୍ୟରେ ଗଠିତ ହେବ । ଏହା ବାସ୍ତବ, ଓଲଟା ଏବଂ ବସ୍ତୁଠାରୁ ସାନ ହେବ ।
![]()
Question 11.
15 ସେ.ମି. ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଗୋଟିଏ ଅବତଳ ଲେନ୍ସ ନିଜଠାରୁ 10 ସେ.ମି. ଦୂରରେ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି କରିଛି । ଲେନ୍ସ ଠାରୁ କେତେ ଦୂରରେ ବସ୍ତୁ ଅଛି ? ରଶ୍ମି ଚିତ୍ର ଅଙ୍କନ କରି ପ୍ରତିବିମ୍ବକୁ ଦେଖାଅ ।
Answer:
ଅବତଳ ଲେନସ୍ର ଫୋକସ୍ ଦୂରତା (f) = – 15 6ସ୍.ମି.
ପ୍ରତିବିମ୍ବର ଦୂରତା v = – 10 6ସ୍.ମି. |
ଲେନ୍ସ ସୂତ୍ର ଅନୁସାରେ : \(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
⇒ \(\frac { 1 }{ u }\) = \(\frac { 1 }{ v }\) – \(\frac { 1 }{ f }\) = \(\frac { 1 }{ (-10) }\) – \(\frac { 1 }{ (-15) }\)
= – \(\frac { 1 }{ 10 }\) + \(\frac { 1 }{ 15 }\) = \(\frac { -3+2 }{ 30 }\) = – \(\frac { 1 }{ 30 }\)
u = -30 6ସ୍.ମି.
∴ ବସ୍ତୁଟି ଲେନ୍ସଠାରୁ 30 ସେ.ମି. ଦୂରରେ ବା 2Fଠାରେ ଅବସ୍ଥିତ !
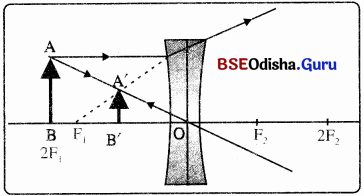
Question 12.
15 ସେମି ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଏକ ଉତ୍ତଳ ଦର୍ପଣଠାରୁ 10 ସେମି ଦୂରରେ ଗୋଟିଏ ବସ୍ତୁ ଅଛି । ଏହାର ପ୍ରତିବିମ୍ବର ସ୍ଥିତି ଓ ପ୍ରକୃତି ନିର୍ଣ୍ଣୟ କର ।
Answer:
ବସ୍ତୁର ଦୂରତା (u) = – 10 6ସ୍.ମି.,
ଫୋକସ୍ ଦୂରତା (f) = + 15 6ସ୍.ମି.,
ପ୍ରତିବିମ୍ବର ଦୂରତା = v
∴ ଦର୍ପଣ ସୂତ୍ର ଅନୁସାରେ :\(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
⇒ \(\frac { 1 }{ v }\) = \(\frac { 1 }{ f }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ 15 }\) + \(\frac { 1 }{ -10 }\) = \(\frac { 1 }{ 15 }\) + \(\frac { 1 }{ 10 }\) = \(\frac { 2+3 }{ 30 }\) = \(\frac { 5 }{ 30 }\) = \(\frac { 1 }{ 6 }\)
∴ v = + 6ସ୍.ମି.,
∴ ପ୍ରତିବିମ୍ବଟି ଦର୍ପଣର ପଛରେ 6 ସେ.ମି. ଦୂରରେ ଗଠିତ ହେବ । ଏହା ଆଭାସୀ, ସଳଖ ଓ ବସ୍ତୁଠାରୁ ସାନ ହେବ ।
Question 13.
ଏକ ସମତଳ ଦର୍ପଣ ଦ୍ବାରା ସୃଷ୍ଟ ପରିବର୍ଦ୍ଧନ +1 ଅଟେ । ଏହାର ଅର୍ଥ କ’ଣ ?
Answer:
ସମତଳ ଦର୍ପଣର ପରିବର୍ତନ (m) : = \(\frac { h’ }{ h }\) = – \(\frac { v }{ u }\)
ଦତ୍ତ ଅଛି ସମତଳ ଦର୍ପଣର m = +1 ହେଲେ h’ = h ଏବଂ v = – u
(a) ପରିବର୍ଦ୍ଧନ + l ର ଅର୍ଥ ପ୍ରତିବିମ୍ବର ଆକାର ବସ୍ତୁର ଆକାର ସହ ସମାନ ।
(b) ପରିବର୍ଦ୍ଧନ + 1 ର ଅର୍ଥ ପ୍ରତିବିମ୍ବ ଆଭାସୀ ଓ ସଳଖ ହେବ ।
Question 14.
30 ସେମି ବଜ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ଉତ୍ତଳ ଦର୍ପଣଠାରୁ 20 ସେମି ଦୂରରେ 5.0 ସେମି ଦୈର୍ଘ୍ୟର ଗୋଟିଏ ବସ୍ତୁ ଅଛି । ପ୍ରତିବିମ୍ବର ସ୍ଥାନ, ପ୍ରକୃତି ଓ ଆକୃତି ନିର୍ଣ୍ଣୟ କର ।
Answer:
ଏଠାରେ ବସ୍ତୁର ଉଚ୍ଚତା (h) = +5 6ସ୍.ମି.,
ବସ୍ତୁର ଦୂରତା (u) = – 20 6ସ୍.ମି.,
ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ (R) = + 30 ସେ.ମି.
ଫୋକସ୍ ଦୂରତା (f) = \(\frac { R }{ 2 }\) = \(\frac { 30 }{ 2 }\) = 15 6ସ୍.ମି.,
ଦର୍ପଣ ପୂତ୍ର ଅନ୍ସାରେ \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
⇒ \(\frac { 1 }{ v }\) + \(\frac { 1 }{ -20 }\) = \(\frac { 1 }{ +15 }\)
⇒ \(\frac { 1 }{ v }\) = \(\frac { 1 }{ 15 }\) + \(\frac { 1 }{ 20 }\) = \(\frac { 4+3 }{ 60 }\) = \(\frac { 7 }{ 60 }\)
⇒ v = \(\frac { 60 }{ 7 }\) = 8.57 6ସ୍.ମି.,
∴ ପ୍ରତିବିମ୍ବଟି ଦର୍ପଣର ପଛରେ 8.57 ବା 8.6 ସେ.ମି. ଦୂରରେ ଗଠିତ ହୋଇଛି ।
ପରିବର୍ତ୍ତନ (m) : \(\frac { h’ }{ h }\) = – \(\frac { v }{ u }\)
⇒ \(\frac { h’ }{ 5 }\) = – \(\frac { 8.57 }{ -20 }\)
⇒ h’ = \(\frac { 8.57×5 }{ -20 }\) = \(\frac { 8.57×5 }{ 20 }\) = 2.1425 ର| 2.14 6ସ୍.ମି.,
∴ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା 2.14 ସେ.ମି. ।
∴ ପ୍ରତିବିମ୍ବ ଆଭାସୀ, ସଳଖ ଓ ବସ୍ତୁଠାରୁ ସାନ ।
![]()
Question 15.
18 ସେମି ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଏକ ଅବତଳ ଦର୍ପଣର 27 ସେମି ସମ୍ମୁଖରେ 7 ସେମି ଆକାରର ବସ୍ତୁ ରଖାଯାଇଛି । ଦର୍ପଣଠାରୁ କେତେ ଦୂରରେ ଏକ ପରଦା ରଖିଲେ ତା’ ଉପରେ ଫୋକସ୍ ହୋଇଥିବା ଏକ ତୀକ୍ଷ୍ଣ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହେବ । ପ୍ରତିବିମ୍ବର ଆକାର ଓ ପ୍ରକୃତି କ’ଣ ହେବ ?
Answer:
ବସ୍ତୁର ଉଚ୍ଚତା (ଆକାର ) h = + 7 ସେ.ମି.,
ଫୋକସ୍ ଦୂରତା f = – 18 ସେ.ମି.
ପ୍ରତିବିମ୍ବର (ଉଚ୍ଚତା) = h’,
ବସ୍ତୁର ଦୂରତା u = – 27 ସେ.ମି.
ବର୍ପଣ ପୃତ୍ର ଅନ୍ତପାପ୍ପା \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
⇒ \(\frac { 1 }{ v }\) + \(\frac { 1 }{ -27 }\) = \(\frac { 1 }{ -18 }\)
⇒ \(\frac { 1 }{ v }\) = \(\frac { 1 }{ -18 }\) + \(\frac { 1 }{ 27 }\) = \(\frac { -1 }{ 18 }\) + \(\frac { 1 }{ 27 }\) = \(\frac { -3+2 }{ 54 }\) = \(\frac { -1 }{ 54 }\)
⇒ v = – 54 ସେ.ମି.,
ଦର୍ପଣଠାରୁ 54 ସେ.ମି. ଦୂରରେ ( ଦର୍ପଣ ଆଗରେ ବସ୍ତୁ ଯେଉଁ ପାର୍ଶ୍ବରେ) ଏକ ପରଦା ରଖିଲେ ତା’ ଉପରେ ଫୋକସ୍ ହୋଇଥିବା ଏକ ତୀକ୍ଷ୍ଣ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହେବ ।
ପରିବର୍ଦ୍ଧନ m = \(\frac { h’ }{ h }\) = \(\frac { – v }{ u }\)
⇒ \(\frac { h’ }{ 7 }\) = – \(\frac { (- 54) }{ (-27) }\)
⇒ h’ = – \(\frac { 54×7 }{ 27 }\) = -14 ସେ.ମି.,
∴ ବାସ୍ତବ, ଓଲଟା ଓ ବର୍ଦ୍ଧିତ ପ୍ରତିବିମ୍ବ ଗଠିତ ହେବ ।
Question 16.
ଗୋଟିଏ ଲେନ୍ସର ପାୱାର – 2.0 D । ଏହାର ଫୋକସ୍ ଦୂରତା କେତେ ? ଏହା କି ପ୍ରକାରର ଲେନ୍ସ ?
Answer:
P = – 2.0 D
P = \(\frac { 1 }{ f }\)
⇒ f = \(\frac { 1 }{ P }\) = \(\frac { 1 }{ -2.0 }\) ମି. = – \(\frac { 1 }{ 2 }\) × 100 ସେ.ମି. = – 50 ସେ.ମି.
∴ ଯେହେତୁ ଲେନ୍ସର ପାୱାର ବିଯୁକ୍ତାତ୍ମକ, ଏହା ଏକ ଅବତଳ ଲେନ୍ସ ।
Question 17.
ଜଣେ ଡାକ୍ତର + 1.5 D ପାୱାରର ସଂଶୋଧନକାରୀ ଲେନ୍ସ ବ୍ୟବହାର କରିବାକୁ ନିର୍ଦ୍ଧାରଣ କରିଛନ୍ତି । ଏହି ଲେନ୍ସର ଫୋକସ୍ ଦୂରତା କେତେ ? ଏହି ନିର୍ଦ୍ଧାରିତ ଲେନ୍ସ ଅପସାରୀ ନା ଅଭିସାରୀ ?
Answer:
P= \(\frac { 1 }{ f }\) ⇒ 1.5 = \(\frac { 1 }{ f }\)
⇒ f = \(\frac { 1 }{ 1.5 }\) ମି. = \(\frac { 10 }{ 15 }\) ମି. = \(\frac { 2 }{ 3 }\) ମି. = + 0.67 ମି.
ଲେନ୍ସର ପାୱାର ଯୁକ୍ତାତ୍ମକ ହେତୁ ଏହା ଏକ ଅଭିସାରୀ ଲେନ୍ସ ।
![]()
ପ୍ରଶ୍ନବଳୀ ଓ ଉତ୍ତର:
Question 1.
ଅବତଳ ଦର୍ପଣର ପ୍ରମୁଖ ଫୋକସ୍ର ସଂଜ୍ଞା କ’ଣ ?
Answer:
ମୁଖ୍ୟ ଅକ୍ଷ ସହିତ ସମାନ୍ତର ଆଲୋକ ରଶ୍ମି ଅବତଳ ଦର୍ପଣରେ ପ୍ରତିଫଳିତ ହୋଇ ଦର୍ପଣର ଆଗରେ ଯେଉଁ ବିନ୍ଦୁରେ ମିଳିତ ହୁଅନ୍ତି ତାହାକୁ ଅବତଳ ଦର୍ପଣର ପ୍ରମୁଖ ଫୋକସ୍ (Principal Focus) କୁହାଯାଏ ।
Question 2.
ଗୋଟିଏ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ 20 ସେ.ମି ହେଲେ ତାହାର ଫୋକସ୍ ଦୂରତା କେତେ ?
Answer:
R = 2f ⇒ f = \(\frac { R }{ 2 }\)

Question 3.
ଗୋଟିଏ ବସ୍ତୁର ସଳଖ ଓ ପରିବର୍ଦ୍ଧିତ ପ୍ରତିବିମ୍ବ ଦେଖାଇ ପାରୁଥିବା ଦର୍ପଣର ନାମ କୁହ ।
Answer:
ଅବତଳ ଦର୍ପଣ ।
Question 4.
ଯାନଗୁଡ଼ିକରେ ପଛପାଖ ଦେଖିବା ପାଇଁ କାହିଁକି ଉତ୍ତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ ?
Answer:
ଉତ୍ତଳ ଦର୍ପଣରେ ସର୍ବଦା ଦୂରରେ ଥିବା ବସ୍ତୁର ସଳଖ ଓ ବସ୍ତୁ ତୁଳନାରେ ଛୋଟ ପ୍ରତିବିମ୍ବ ଗଠିତ ହେଉଥିବାରୁ ବିସ୍ତୀର୍ଣ୍ଣ ଅଞ୍ଚଳର ପ୍ରତିବିମ୍ବ ଦେଖହୁଏ । ତେଣୁ ଯାନଗୁଡ଼ିକରେ ଉତ୍ତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ ।
Question 5.
ଗୋଟିଏ ଉତ୍ତଳ ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା ନିର୍ଣ୍ଣୟ କର, ତାହାର ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ 32 ସେ.ମି. ଅଟେ |
Answer:
ଯେହେତୁ ଉତ୍ତଳ ଦର୍ପଣରେ ଫୋକସ୍ ଦୂରତା ଓ ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ (+) ଧନାତ୍ମକ, ତେଣୁ R = 32 ସେ.ମି.
R = 2f ⇒ f = \(\frac { R }{ 2 }\) = f = \(\frac { 32 }{ 2 }\) = 16 ସେ.ମି.,
∴ ଉତ୍ତଳ ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା 16 ସେ.ମି. ।
Question 6.
ଗୋଟିଏ ଅବତଳ ଦର୍ପଣ ସାମନାରେ 10 ସେ.ମି. ଦୂରରେ ଗୋଟିଏ ବସ୍ତୁ ରଖୁ, ସେହି ଦର୍ପଣ 3 ଗୁଣ ପରିବର୍ଦ୍ଧିତ ବାସ୍ତବ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି କରେ । ପ୍ରତିବିମ୍ବର ଅବସ୍ଥିତି ନିର୍ଣ୍ଣୟ କର ।
Answer:
ଯେହେତୁ ପ୍ରତିବିମ୍ବ ବାସ୍ତବ ତେଣୁ ପରିବର୍ତ୍ତନ ବିଯୁକ୍ତାତ୍ମକ (–) l m = – 3 ଏବଂ u = – 10 ସେ.ମି. ।
⇒ m = \(\frac { h’ }{ h }\) = – \(\frac { v }{ u }\) ⇒ – 3 = – \(\frac { v }{ u }\)
⇒ v = 3 x u = 3 x (-10) = – 30 ସେ.ମି.
∴ ଦର୍ପଣଠାରୁ 30 ସେ.ମି. ଦୂରରେ ବସ୍ତୁଥିବା ପାର୍ଶ୍ଵରେ ପ୍ରତିବିମ୍ବ ଗଠିତ ହେବ ।
Question 7.
ବାୟୁରେ ଗତି କରୁଥିବା ଏକ ଆଲୋକ ରଶ୍ମି ତୀର୍ଯ୍ୟକ୍ ଭାବରେ ଜଳରେ ପ୍ରବେଶ କଲେ ସେହି ରଶ୍ମି ମାଧ୍ୟମ ଦ୍ବୟର ବ୍ୟବଧାନ ପୃଷ୍ଠରେ ଅଭିଲମ୍ବ ଆଡ଼କୁ ବାଙ୍କିଯିବ ନା ଅଭିଲୟଠାରୁ ଦୂରକୁ ବାଙ୍କିଯିବ ? ଏପରି କାହିଁକି ହେବ ?
Answer:
ଆଲୋକ ରଶ୍ମି ଅଭିଲମ୍ବ ଆଡ଼କୁ ବାଙ୍କିଯିବ । କାରଣ ଆଲୋକର ବେଗ ବାୟୁ ତୁଳନାରେ ଜଳରେ କମ୍ ! ବେଗ ହ୍ରାସ ହେଉଥିବାରୁ ଅଭିଲମ୍ବ ଆଡ଼କୁ ବଙ୍କେଇ ଯାଏ ।
Question 8.
ଆଲୋକ 1.50 ପ୍ରତିସରଣାଙ୍କ ବିଶିଷ୍ଟ କାଚ ମଧ୍ୟକୁ ପ୍ରବେଶ କଲା । କାଚ ଭିତରେ ଆଲୋକର ବେଗ କେତେ ହେବ ? (ଶୂନ୍ୟରେ ଆଲୋକର ବେଗ 3 x 10 ମି.ସେ – ଅଟେ ।
Answer:
କାଚର ପ୍ରତିସରଣାଙ୍କ ng = 1.50
ଆଲୋକର ବାୟୁରେ ବେଗ (C) = 3 x 108 ମି. ସେ
ଆଲୋକର କାଚ ମାଧ୍ୟମରେ ବେଗ = Vg

Question 9.
6.3 ସାରଣୀ ଦେଖୁ କୁହ କେଉଁ ମାଧ୍ୟମର ଆଲୋକୀୟ ଘନତା ସର୍ବାଧିକ ଓ କେଉଁ ମାଧ୍ୟମରେ ଆଲୋକୀୟ ଘନତା ସର୍ବନିମ୍ନ ?
Answer:
ହୀରାର ପ୍ରତିସରଣାଙ୍କ ସର୍ବାଧ୍ଵ (2.42) ହୋଇଥିବାରୁ ଏହାର ଆଲୋକୀୟ ଘନତା ସର୍ବାଧିକ । ବାୟୁର ପ୍ରତିସରଣାଙ୍କ ସର୍ବନିମ୍ନ (1.0003) ହୋଇଥିବାରୁ ବାୟୁର ଆଲୋକୀୟ ଘନତା ସର୍ବନିମ୍ନ ।
![]()
Question 10.
ତୁମକୁ କିରୋସିନି, ଟରପେନଟାଇନ୍ ତେଲ ଓ ଜଳ ଦିଆଗଲା । ଏହା ମଧ୍ୟରୁ କାହା ଭିତରେ ଆଲୋକ ସବୁଠାରୁ ଅଧିକ ବେଗରେ ଗତି କରିବ ? (6.3 ସାରଣୀର ତଥ୍ୟକୁ ଏଥିପାଇଁ ବ୍ୟବହାର କର )
Answer:
କିରୋସିନ୍ର n = 1.44,
ଟରପେନ୍ଟାଇନ୍ର n = 1.47 ଏବଂ ଜଳର n = 1.33
ଯେଉଁ ମାଧ୍ୟମରେ ପ୍ରତିସରଣାଙ୍କ ସର୍ବନିମ୍ନ, ସେହି ମାଧ୍ୟମରେ ଆଲୋକର ବେଗ ସର୍ବାଧିକ ।
ଏଠାରେ ଜଳର ପ୍ରତିସରଣାଙ୍କ ସର୍ବନିମ୍ନ ହୋଇଥିବାରୁ ଜଳର ଆଲୋକୀୟ ଘନତା ସର୍ବନିମ୍ନ । ତେଣୁ ଜଳ ଭିତରେ ଆଲୋକ ସବୁଠାରୁ ଅଧ୍ଵ ବେଗରେ ଗତି କରିବ ।
Question 11.
ହୀରାର ପ୍ରତିସରଣାଙ୍କ (2.42) ଅଟେ । ଏହାର ଅର୍ଥ କ’ଣ ?
Answer:
ହୀରାର ଆଲୋକୀୟ ଘନତା ସର୍ବାଧିକ । ହୀରା ଭିତରେ ଆଲୋକ ସବୁଠାରୁ କମ୍ ବେଗରେ ଗତି କରେ । ଏହା ଆଲୋକର ବାୟୁରେ ବେଗ ଓ ହୀରାରେ ବେଗର ଅନୁପାତକୁ ବୁଝାଏ ।
Question 12.
1 ଡାୟପ୍ଟରର ସଂଜ୍ଞା କ’ଣ ?
Answer:
1 ମିଟର ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଲେନସ୍ର ପାୱାରକୁ 1 ଡାୟପ୍ଟର କହନ୍ତି ।
Question 13.
ଗୋଟିଏ ଉତ୍ତଳ ଲେନ୍ସ ଏକ ଛୁଞ୍ଚିର ବାସ୍ତବ ଓ ଓଲଟା ପ୍ରତିବିମ୍ବ ଲେନ୍ସଠାରୁ 50 ସେ.ମି. ଦୂରରେ ସୃଷ୍ଟି କରେ । ଉତ୍ତଳ ଲେନ୍ସ ସମ୍ମୁଖରେ କେଉଁ ସ୍ଥାନରେ ଛୁଞ୍ଚିକୁ ରଖେ, ପ୍ରତିବିମ୍ବର ଆକାର ବସ୍ତୁର ଆକାର ସହିତ ସମାନ ହେବ । ଲେନ୍ସର ପାୱାର କେତେ ତାହା ମଧ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Answer:
ଏଠାରେ ବାସ୍ତବ ପ୍ରତିବିମ୍ବର ଦୂରତା v = + 50 ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ ପ୍ରତିବିମ୍ବର ଆକାର = ବସ୍ତୁର ଆକାର ⇒ h’ = h
m = \(\frac { h’ }{ h }\) = – 1
∴ \(\frac { v }{ u }\) = – 1 ⇒ u = – v = – 50 ସେ.ମି.
ପ୍ରତିବିମ୍ବର ଦୂରତା = 50 ସେ.ମି.
\(\frac { 1 }{ f }\) = \(\frac { 1 }{ v }\) – \(\frac { 1 }{ v }\) = + \(\frac { 1 }{ 50 }\) + \(\frac { 1 }{ 50 }\) = + \(\frac { 2 }{ 50 }\) = + \(\frac { 1 }{ 25 }\) ସେ.ମି.
⇒ f = 25 ସେ.ମି. = 0.25 ମିଟର
P = \(\frac { 1 }{ f }\) = \(\frac { 1 }{ 0.25 }\) ମିଟର = 4 ଡାୟପ୍ଟର
∴ ଲେନ୍ସର ପାୱାର 4 ଡାୟପ୍ଟର ।
Question 14.
ଗୋଟିଏ ଅବତଳ ଲେନ୍ସର ଫୋକସ୍ ଦୂରତା 2.0 ମି ହେଲେ ତାହାର ପାୱାର କେତେ ?
Answer:
ଅବତଳ ଲେନସ୍ର ଫୋକସ୍ ବିଯୁକ୍ତାତ୍ମକ f = – 2 ମିଟର
p = \(\frac { 1 }{ f }\) = – \(\frac { 1 }{ 2 }\) ମିଟର = – 0.5 ଡାୟପୁର ।
କାର୍ଯ୍ୟାବଳୀ (Activity):
କାର୍ଯ୍ୟାବଳୀ -1 (Activity-1)
ଆବଶ୍ୟକ ଉପକରଣ : ଚକ୍ ଚକ୍ କରୁଥିବା ଗୋଟିଏ ବଡ଼ ଚାମଚ ।
ପରୀକ୍ଷଣ :
- ବକ୍ରପୃଷ୍ଠରେ ତୁମର ମୁହଁକୁ ଦେଖିବାକୁ ଚେଷ୍ଟାକର ।
- ଚାମଚକୁ ତୁମ ମୁହଁ ପାଖରୁ ଧୀରେ ଧୀରେ ଦୂରେଇ ନିଆଯାଉ ।
- ଚାମଚକୁ ଓଲଟାଇ ଦେଇ ସେଥିରେ ମୁହଁ ଦେଖାଯାଉ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ :
- ଚାମଚକୁ ଓଲଟାଇ ଦେଇ ସେଥିରେ ମୁହଁ ଦେଖାଯାଉ । ଚାମଚର ବଜ୍ରପୃଷ୍ଠରେ ଏକ ଓଲଟା ଓ ବର୍ଦ୍ଧିତ ପ୍ରତିବିମ୍ବ ଦେଖାଗଲା ।
- ଚାମଚକୁ ମୁହଁ ପାଖରୁ ଧୀରେ ଧୀରେ ଦୂରେଇ ନେବାଦ୍ଵାରା ପ୍ରତିବିମ୍ବ ଧୀରେ ଧୀରେ କ୍ଷୁଦ୍ର ହୋଇଗଲା ।
- ଚାମଚକୁ ଓଲଟାଇ ଦେଇ ସେଥିରେ ମୁହଁ ଦେଖିଲେ ମୁହଁର ଏକ ସଳଖ ଓ କ୍ଷୁଦ୍ର ପ୍ରତିବିମ୍ବ ଦେଖାଗଲା ।
ସିଦ୍ଧାନ୍ତ :
ଚାମଚଠାରୁ ବସ୍ତୁର ଅବସ୍ଥାନ ପରିବର୍ତ୍ତନ ହେଲେ ପ୍ରତିବିମ୍ବର ଆକାର ପରିବର୍ତ୍ତିତ ହୁଏ ।
କାର୍ଯ୍ୟାବଳୀ -2 (Activity-2)
ଗୋଟିଏ ଅବତଳ ଦର୍ପଣକୁ ସୂର୍ଯ୍ୟ ଆଡ଼କୁ ଦେଖାଅ । ସୂର୍ଯ୍ୟ ରଶ୍ମିଗୁଡ଼ିକର ପ୍ରତିଫଳିତ ରଶ୍ମି ବାହାରୁଛି । ଖଣ୍ଡେ କାଗଜଆଣି ଏହି ପ୍ରତିଫଳିତ ରଶ୍ମିଗୁଡ଼ିକୁ ତା’ ଉପରେ ପକାଅ ଏବଂ କାଗଜକୁ ଆଗପଛ କର । ଗୋଟିଏ ଅତି ଉଜ୍ଜ୍ବଳ ଆଲୋକ ବିନ୍ଦୁ କାଗଜର ଗୋଟିଏ ସ୍ଥାନରେ ପଡ଼ୁଛି । କିଛି ସମୟ ଏହିପରି ରଖୁ ଦେଖୁର କାଗଜଟି ଜଳି ଉଠିବ । ଉଜ୍ଜ୍ବଳ ଆଲୋକ ବିନ୍ଦୁ ହେଉଛି ଅବତଳ ଦର୍ପଣର ଫୋକସ୍ (F) । F ବିନ୍ଦୁରେ ସୂର୍ଯ୍ୟର ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହୋଇଛି (ବାସ୍ତବ, ଓଲଟା ଓ ଛୋଟ ପ୍ରତିବିମ୍ବ) । କାଗଜ ଉପରେ ଫୋକସ୍ ବିନ୍ଦୁରେ ସୃଷ୍ଟି ହୋଇଥିବା ପ୍ରତିବିମ୍ବ ଓ ଦର୍ପଣ ମଧ୍ୟରେ ରହିଥିବା ଦୂରତା ହିଁ ଦର୍ପଣର ସନ୍ନିକଟ (Approximate) ଫୋକସ୍ ଦୂରତା ।
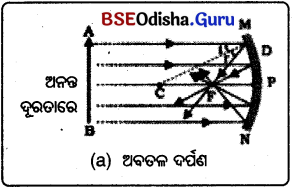
କାର୍ଯ୍ୟାବଳୀ -3 (Activity-3)
ବସ୍ତୁର ବିଭିନ୍ନ ଅବସ୍ଥାନ ପାଇଁ ଅବତଳ ଦର୍ପଣରେ ପ୍ରତିବିମ୍ବ ଗଠନ ।
ଆବଶ୍ୟକ ଉପକରଣ :
ଅବତଳ ଦର୍ପଣ, ମିଟରସ୍କେଲ, ଚକ୍ଖଣ୍ଡ, ଜଳନ୍ତା ମହମବତୀ, କାଗଜ ପରଦା ।
ପରୀକ୍ଷଣ :
ଗୋଟିଏ ଅବତଳ ଦର୍ପଣ ନିଅ, ଏହାର ଫୋକସ ଦୂରତାର ସନ୍ନିକଟ ମାନ (approximate value) ନିର୍ଣ୍ଣୟ କରି ଟିପି ରଖ ।
ତୁମେ କୌଣସି ଦୂରବର୍ତ୍ତୀ ବସ୍ତୁର ପ୍ରତିବିମ୍ବକୁ ଏକ ସାଧା କାଗଜ ପରଦା ଉପରେ ଦେଖ୍ ଦର୍ପଣର ଫୋକସ୍ ଦୂରତାର ସନ୍ନିକଟମାନ ମଧ୍ୟ ନିର୍ଣ୍ଣୟ କରିପାରିବ ।
ଟେବୁଲ ଉପରେ ଚଦ୍ଵାରା ଏକ ରେଖା ଟଣାଯାଉ ।
ଏକ ଅବତଳ ଦର୍ପଣକୁ ଷ୍ଟାଣ୍ଡରେ ଲଗାଇ ଟାଣିଥ୍ ରେଖା ଉପରେ ଏପରି ରଖ ଯେପରିକି ଦର୍ପଣର ପୋଲ୍ ଠିକ୍ ରେଖା ଉପରେ ରହିବ।
ପୂର୍ବରେଖା ସହିତ ସମାନ୍ତର ଭାବରେ ଆଉ ଦୁଇଟି ରେଖା ଟାଣ ଯେମିତି ପାଖାପାଖୁ ଯେକୌଣସି ଦୁଇଟି ରେଖା ମଧ୍ଯରେ ଦୂରତା ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା ସହିତ ସମାନ ହେବ ।
ଏହି ରେଖାତ୍ରୟର ସ୍ଥିତି ବର୍ତ୍ତମାନ ଦର୍ପଣର ପୋଲ୍ (P), ଫୋକସ୍ ବିନ୍ଦୁ (F) ଓ ବକ୍ରତା କେନ୍ଦ୍ର (C) ଭେଦ କରିବ ।
କାରଣ କ୍ଷୁଦ୍ରଦ୍ଵାରକ ବିଶିଷ୍ଟ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ଫୋକସ୍ ବିନ୍ଦୁ (F), ତା’ର ପୋଲ୍ (P) ଓ ବକ୍ରତାକେନ୍ଦ୍ର (C)ର ମଝିରେ ଥାଏ ।
ଜଳୁଥିବା ମହମବତୀ ନିଆଯାଉ । ମହମବତୀକୁ ୯ ବିନ୍ଦୁର ପଛକୁ ଦୂରରେ ରଖ । ଦର୍ପଣ ସାମନାରେ ଏକ କାଗଜ ପରଦା ରଖ । ପରଦା(Screen)କୁ ଆଗପଛ କରି ଯେଉଁ ସ୍ଥାନରେ ଉଜ୍ଜ୍ବଳ, ତୀକ୍ଷ୍ଣ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହେବ ତା’ର ପ୍ରକୃତି ଓ ସ୍ଥିତିକୁ ଟିପି ରଖ ।
ମହମବତୀର ଆକାର ସହିତ ପ୍ରତିବିମ୍ବର ଆକାର ତୁଳନା କର । ଜଳନ୍ତା ମହମବତୀକୁ
(a) C ଠାରୁ ଅଳ୍ପ ଦୂରରେ, (b) ଠିକ୍ C ଉପରେ (c) F ଓ C ମଧ୍ୟରେ (d) ଠିକ୍ F ଉପରେ,
(e) P ଓ F ମଧ୍ୟରେ ରଖ୍ ପ୍ରତିବିମ୍ବର ଅବସ୍ଥାନ ଓ ପ୍ରକୃତି ନିର୍ଣ୍ଣୟ କର ।
ପର୍ଯ୍ୟବେକ୍ଷଣ :
ଅବତଳ ଦର୍ପଣଦ୍ୱାରା ସୃଷ୍ଟି ହେଉଥିବା କୌଣସି ବସ୍ତୁର ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି, ଅବସ୍ଥାନ ଓ ଆକାର ଦର୍ପଣ ସେହି ବସ୍ତୁର ଅବସ୍ଥାନ ଉପରେ ନିର୍ଭର କରେ ।
ବସ୍ତୁର ଅବସ୍ଥାନକୁ P, F ଓ C ବିଦୁ୍ୟତ୍ରୟକୁ ଭିତ୍ତିକରି ପ୍ରକାଶ କରାଯାଇଛି ।
ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ବାସ୍ତବ ବା ଆଭାସୀ, ସଳଖ ବା ଓଲଟା କିମ୍ବା ବସ୍ତୁ ସହିତ ସମାନ, ଛୋଟ ବା ବଡ଼ ହୋଇପାରେ ।
ଅବତଳ ଦର୍ପଣରେ ବସ୍ତୁର ଭିନ୍ନ ଭିନ୍ନ ସ୍ଥିତିପାଇଁ ପ୍ରତିବିମ୍ବ ଗଠନ :
ସିଦ୍ଧାନ୍ତ :
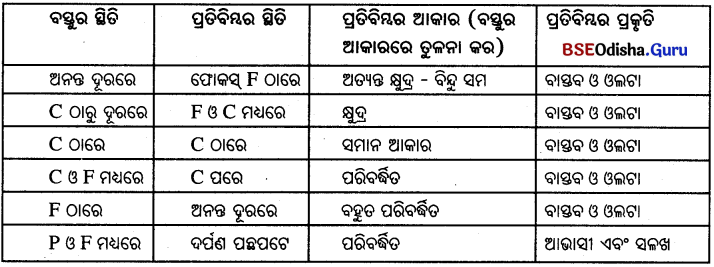
କାର୍ଯ୍ୟାବଳୀ -4 (Activity-4)
ବସ୍ତୁର ନିମ୍ନଲିଖତ ଅବସ୍ଥିତି ପାଇଁ ସ୍କେଲ୍ ଓ ପେନ୍ସିଲ୍ ବ୍ୟବହାର କରି ରଶ୍ମିଚିତ୍ର ଅଙ୍କନ କର ।
(a) ଅନନ୍ତ ଦୂରତାରେ
(b) C ଠାରୁ ଦୂରରେ (ବକ୍ରତା କେନ୍ଦ୍ରଠାରୁ ଦୂରରେ)
(c) C ଠାରେ (ବକ୍ରତା କେନ୍ଦ୍ରଠାରେ)
(d) C ଓ F ମଧ୍ୟରେ (ବକ୍ରତା କେନ୍ଦ୍ର ଓ ପ୍ରମୁଖ ଫୋକସ୍ ମଧ୍ୟରେ)
(e) F ଠାରେ (ପ୍ରମୁଖ ଫୋକସଠାରେ)
(f) P ଓ F (ପୋଲ୍ ଓ ଫୋକସ ମଧ୍ଯରେ)
(a) ଅନନ୍ତ ଦୂରତାରେ ଥିବା ବସ୍ତୁର ପ୍ରତିବିମ୍ବ :
(i) ଅନନ୍ତ ଦୂରତାରେ ଥିବା ବସ୍ତୁରୁ ଆସୁଥିବା ଆଲୋକ ରଶ୍ମି ଦର୍ପଣ ପୃଷ୍ଠରେ ଆପତିତ ହୋଇ ପ୍ରତିଫଳିତ ରଶ୍ମି ଫୋକସ୍ ମଧ୍ୟଦେଇ ଗଚିକରିଚ୍ଚି |
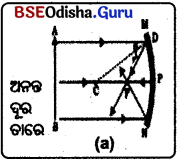
(ii) C ମଧ୍ୟଦେଇ ବସ୍ତୁରୁ ଆସୁଥିବା ଆଲୋକ ରଶ୍ମି ପୁନର୍ବାର C ମଧ୍ୟଦେଇ ଫେରିଯାଏ ।
(iii) ଏହି ରଶ୍ମିଦ୍ଵୟ ପରସ୍ପରକୁ F ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
(iv) ପ୍ରତିବିମ୍ବର ଅବସ୍ଥାନ – ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ଦର୍ପଣର ଫୋକସ୍ (F) ଠାରେ ସୃଷ୍ଟି ହେବ ।
(v) ପ୍ରତିବିମ୍ବର ପ୍ରକୃତ ଆକାର– ବାସ୍ତବ ଓ ଓଲଟା ଓ ବସ୍ତୁଠାରୁ ଅତ୍ୟନ୍ତ କ୍ଷୁଦ୍ର ବିନ୍ଦୁ ସମ ।
(b) C ଠାରୁ ଦୂରରେ ଥିବା ବସ୍ତୁର ପ୍ରତିବିମ୍ବ :
(i) AB ବସ୍ତୁଟି C ଠାରୁ ଦୂରରେ ରହିଛି ।
(ii) ଏଠାରେ A ବିନ୍ଦୁରୁ AM ରଶ୍ମିଟି ଦର୍ପଣର ଅକ୍ଷ ସହ ସମାନ୍ତର ଓ ଏହାର ପ୍ରତିଫଳିତ ରଶ୍ମି F ବିନ୍ଦୁ ମଧ୍ୟଦେଇ ଗତି କରିଛି ।
(iii) A ଠାରୁ C ମଧ୍ୟଦେଇ ଯାଇଥିବା ଆଲୋକ ରଶ୍ମି ପ୍ରତିଫଳିତ ହୋଇ ସେହିବାଟେ ଫେରିଅଛି ।
(iv) ଏହି ଦୁଇଟି ରଶ୍ମି A’ ବିନ୍ଦୁରେ ଛେଦ କରିବାଦ୍ୱାରା ସେଠାରେ A ର ପ୍ରତିବିମ୍ବ ଗଠିତ ହୋଇଛି । ସେହିପରି AB ବସ୍ତୁର ସମସ୍ତ ବିନ୍ଦୁପାଇଁ A’B’ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୋଇଛି ।
ପ୍ରତିବିମ୍ବର ଅବସ୍ଥାନ – F ଓ C ମଧ୍ୟରେ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୋଇଛି ।
ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି ଓ ଆକାର – ପ୍ରତିବିମ୍ବଟି ବାସ୍ତବ, ଓଲଟା ଓ ସବୁଠାରୁ ଛୋଟ ।
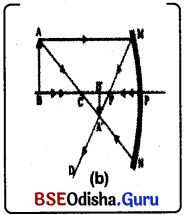
(c) ବସ୍ତୁର ଅବସ୍ଥାନ C ଠାରେ :
(i) AB ବସ୍ତୁଟି ବକ୍ରତା କେନ୍ଦ୍ରଠାରେ ଅଛି ।
(ii) A ଠାରୁ ଏକ ରଶ୍ମି AD ମୁଖ୍ୟ ଅକ୍ଷସହ ସମାନ୍ତର ଓ ପ୍ରତିଫଳିତ ହୋଇ F ମଧ୍ୟଦେଇ ଗତିକରିଛି ।
(iii) ଅନ୍ୟ ଏକ ରଶ୍ମି AE ଫୋକସ୍ ମଧ୍ୟଦେଇ ଦର୍ପଣରେ ପ୍ରତିଫଳିତ ହୋଇ ମୁଖ୍ୟ ଅକ୍ଷ ସହ ସମାନ୍ତର ହୋଇ ଗତିକରିଛି ।
(iv) ଦୁଇଟି ପ୍ରତିଫଳିତ ରଶ୍ମି ପରସ୍ପରକୁ A’ ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । ତେଣୁ A’ ହେଉଛି A ର ପ୍ରତିବିମ୍ବ । A’ ଠାରେ ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ଗଠିତ ହୋଇଛି । A’B’ ମୁଖ୍ୟ ଅକ୍ଷପ୍ରତି ଅଭିଲମ୍ବ I A’B’ ଓ AB ଏକ ସରଳରେଖାରେ ଅବସ୍ଥାନ କରନ୍ତି ।
ପ୍ରତିବିମ୍ବର ଅବସ୍ଥାନ – ପ୍ରତିବିମ୍ବ C ଠାରେ ଗଠିତ ହେବ ।
ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି ଓ ଆକାର – ପ୍ରତିବିମ୍ବଟି ବାସ୍ତବ, ଓଲଟା ଏବଂ ବସ୍ତୁସହ ସମାନ ଆକାର ହେବ ।
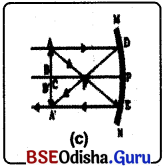
(d) ବସ୍ତୁର ଅବସ୍ଥାନ C ଓ F ମଧ୍ୟରେ :
(i) AB ବସ୍ତୁଟି ଫୋକସ୍ F ଓ ବକ୍ରତା କେନ୍ଦ୍ର C ମଧ୍ୟରେ ରଖାଯାଏ ।
(ii) AB ବସ୍ତୁର A ବିନ୍ଦୁରୁ ଆଲୋକ ରଶ୍ମି AD ପ୍ରତିଫଳିତ ହୋଇ I ବିନ୍ଦୁ ମଧ୍ୟଦେଇ ଯାଏ ।
(iii) ବସ୍ତୁର A ବିନ୍ଦୁରୁ ଅନ୍ୟ ଏକ ଆଲୋକ ରଶ୍ମି AE, Eଠାରେ ପ୍ରତିଫଳିତ ହୋଇ ସେହି ଦିଗରେ ଫେରିଆସିଲା ।
(iv) ରଶ୍ମିଦ୍ବୟ ପରସ୍ପରକୁ A’ ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ଓ A’B’ ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ।
ପ୍ରତିବିମ୍ବର ଅବସ୍ଥାନ – C ପରେ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୋଇଛି ।
ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି ଓ ଆକାର – ପ୍ରତିବିମ୍ବଟି ବାସ୍ତବ, ଓଲଟା ଏବଂ ପ୍ରତିବିମ୍ବଟି ବସ୍ତୁଠାରୁ ପରିବର୍ଦ୍ଧିତ ।
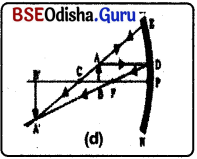
(e) ପ୍ରମୁଖ ଫୋକସ୍ F ଠାରେ ବସ୍ତୁର ଅବସ୍ଥାନ :
(i) AB ବସ୍ତୁଟି ପ୍ରମୁଖ ଫୋକସ୍ F ଠାରେ ଅବସ୍ଥିତ ।
(ii) AD ରଶ୍ମି ମୁଖ୍ୟ ଅକ୍ଷ ସହସମାନ୍ତର ଓ ଅବତଳ ଦର୍ପଣରେ ପ୍ରତିଫଳିତ ହୋଇ ଫୋକସ୍ ମଧ୍ୟ ଦେଇ ଗତିକରେ ।
(iii) ଅନ୍ୟ ଏକ ରଶ୍ମି AE ଅବତଳ ଦର୍ପଣର E ଠାରେ ଆପତିତ ହୋଇ ସେହି ଦିଗରେ ଫେରିଆସେ ଓ C ମଧ୍ୟଦେଇ ଯାଏ ।
(iv) ଏ କ୍ଷେତ୍ରରେ ଦୁଇଟି ପ୍ରତିଫଳିତ ରଶ୍ମି ପରସ୍ପର ସମାନ୍ତର ଏବଂ ଅନନ୍ତ ଦୂରତାରେ ପରସ୍ପର ସହ ମିଳିତ ହୁଅନ୍ତି ।
ପ୍ରତିବିମ୍ବର ଅବସ୍ଥା – ପ୍ରତିବିମ୍ବଟି ଅନନ୍ତ ଦୂରରେ ଗଠିତ ହୁଏ ।
ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି ଓ ଆକାର – ପ୍ରତିବିମ୍ବଟି ସବୁଠାବୁ ରହ୍ତତ ପରିବର୍ଷିତ, ବାସ୍ତବ ଓ ଓଲଟା ।
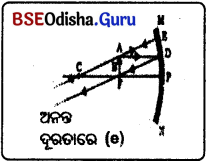
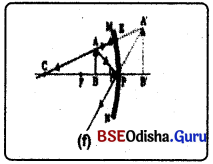
(f) ବସ୍ତୁର ଅବସ୍ଥାନ P ଓ I ମଧ୍ୟରେ ଥିଲେ :
(i) AB ବସ୍ତୁର A ବିନ୍ଦୁରୁ ଆସୁଥିବା ଆଲୋକ ରଶ୍ମି ମୁଖ୍ୟ ଅକ୍ଷସହ ସମାନ୍ତର ହୋଇ ଫୋକସ୍ ମଧ୍ୟଦେଇ ଗତିକରେ ।
(ii) CA ସରଳରେଖା ଦିଗରେ A ବିନ୍ଦୁରୁ ବାହାରୁଥିବା ଅନ୍ୟ ଏକ ଆଲୋକ ରଶ୍ମି E ଠାରେ ଆପତିତ ହୋଇ EC ବାଟେ ପ୍ରତିଫଳିତ ହୋଇ ଫେରୁଛି ।
(iii) ଏହି ଦୁଇ ରଶ୍ମି ଦର୍ପଣର ସମ୍ମୁଖରେ ପରସ୍ପରକୁ
(iv) ଏହି ରଶ୍ମି ଦ୍ଵୟକୁ ବଢ଼ାଇଲେ ଦର୍ପଣର ପଛପଟେ K ଠାରେ ଛେଦ କଲାପରି ଜଣାପଡୁଛି ।
ପ୍ରତିବିମ୍ବର ଅବସ୍ଥା – ଦର୍ପଣର ପଛପଟେ ସୃଷ୍ଟି ହୋଇଛି ।
ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି ଓ ଆକାର – ଆଭାସୀ ଏବଂ ସଳଖ ପ୍ରତିବିମ୍ବ ଗଠିତ ହେବ । ପ୍ରତିବିମ୍ବର ଆକାର ପରିବର୍ଦ୍ଧିତ ହେବ।
(i) ଟର୍ଚ୍ଚ, ସନ୍ଧାନୀ ଆଲୋକ (Search light) ଓ ଯାନଗୁଡ଼ିକର ଶୀର୍ଷ ଆଲୋକରେ ଶକ୍ତିଶାଳୀ ସମାନ୍ତର ଆଲୋକ ଗୁଚ୍ଛ ପାଇବା,ପାଇଁ ଅବତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ ।
(ii) ଦାଢ଼ିକାଟିଲା ବେଳେ ମୁହଁର ବଡ଼ ପ୍ରତିବିମ୍ବ ଦେଖୁବାପାଇଁ ଅବତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ ।
(iii) ଦନ୍ତ ଚିକିତ୍ସକମାନେ ରୋଗୀର ଦାନ୍ତର ବଡ଼ ପ୍ରତିବିମ୍ବ ଦେଖୁବାପାଇଁ ଅବତଳ ଦର୍ପଣ ବ୍ୟବହାର କରନ୍ତି ।
(iv) ସୌର ଚୁଲ୍ଲା (Furnace) ରେ ସୂର୍ଯ୍ୟାଲୋକକୁ କେନ୍ଦ୍ରୀଭୂତ କରାଇ ତାପ ସୃଷ୍ଟି କରିବାପାଇଁ ବଡ଼ ବଡ଼ ଅବତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ ।
(v) ଜ୍ୟୋତିର୍ବିଜ୍ଞାନୀ ଦୂରବୀକ୍ଷଣ ଯନ୍ତ୍ରରେ ଅବତଳ ଦର୍ପଣ ବ୍ୟବହୃତ ହୁଏ ।
(vi) ଚକ୍ଷୁ ପରୀକ୍ଷା ଯନ୍ତ୍ରରେ ଅବତଳ ଦର୍ପଣ ବ୍ୟବହୃତ ହୁଏ ।
ଅବତଳ ଦର୍ପଣରେ ବସ୍ତୁର ଅବସ୍ଥାନ ଓ ତା’ର ପ୍ରତିବିମ୍ବର ସାରାଂଶ :
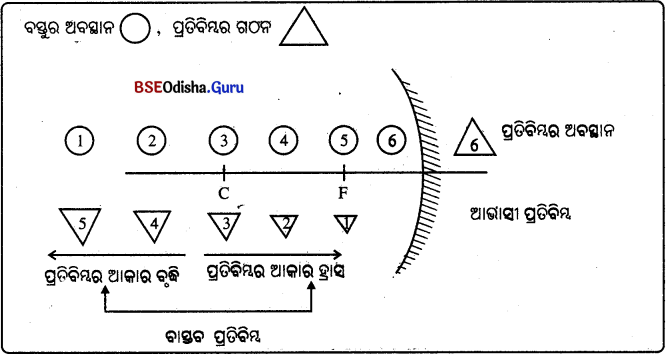
କାର୍ଯ୍ୟାବଳୀ – 5 (Activity – 5)
ଆବଶ୍ୟକ ଉପକରଣ : ଉତ୍ତଳ ଦର୍ପଣ, ପେନ୍ସିଲ୍
ପରୀକ୍ଷଣ :
- ଗୋଟିଏ ଉତ୍ତଳ ଦର୍ପଣ ନିଅ, ଏହାକୁ ଗୋଟିଏ ହାତରେ ଧର ।
- ଦର୍ପଣ ସାମନାରେ ଗୋଟିଏ ପେନ୍ସିଲ୍କୁ ସଳଖ ଭାବରେ (Up right) ଅନ୍ୟ ହାତରେ ଧର ।
- ଦର୍ପଣରେ ପେନ୍ସିଲ୍ର ପ୍ରତିବିମ୍ବକୁ ଦେଖ ।
- ପେନ୍ସିଲ୍କୁ ଧୀରେ ଧୀରେ ଦର୍ପଣଠାରୁ ଦୂରକୁ ନିଅ । ପେନ୍ସିଲ୍କୁ ଧୀରେ ଧୀରେ ଦର୍ପଣ ପାଖକୁ ଆଣ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ :
- ପେନ୍ସିଲ୍କୁ ସଳଖ ଭାବରେ ହାତରେ ଧରି ପ୍ରତିବିମ୍ବକୁ ଲକ୍ଷ୍ୟ କଲେ ପ୍ରତିବିମ୍ବଟି ପେନସିଲ୍ ଠାରୁ ସାନ ଓ ସଳଖ ହେବ ।
- ପେନ୍ସିଲ୍କୁ ଧୀରେ ଧୀରେ ଦର୍ପଣଠାରୁ ଦୂରକୁ ନେଲେ ପ୍ରତିବିମ୍ବର ଆକାର ଧୀରେ ଧୀରେ ଛୋଟ ହେବ ।
- ପେନ୍ସିଲ୍କୁ ଧୀରେ ଧୀରେ ଦର୍ପଣ ଆଡ଼କୁ ଆଣିଲେ ପ୍ରତିବିମ୍ବର ଆକାର ଧୀରେ ଧୀରେ ବଢ଼ିବ ଏବଂ ପ୍ରତିବିମ୍ବ ପୋଲ୍ ଆଡ଼କୁ ଗତିକରିବ ଓ ଶେଷରେ ବସ୍ତୁର ଆକାର ଏବଂ ପ୍ରତିବିମ୍ବର ଆକାର ସମାନ ହେବ ।
- ବସ୍ତୁକୁ ଦର୍ପଣଠାରୁ ଦୂରେଇ ନେଲେ ତା’ର ପ୍ରତିବିମ୍ବ ଫୋକସ୍ଡ଼କୁ ଗତିକରିବ ।
ସିଦ୍ଧାନ୍ତ :
- ଅବତଳ ଦର୍ପଣରେ ସର୍ବଦା ଆଭାସୀ, ସଳଖ ଓ ବସ୍ତୁଠାରୁ କ୍ଷୁଦ୍ର ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ ।
- ପ୍ରତିବିମ୍ବ ସର୍ବଦା P ଓ F ମଧ୍ଯରେ ଗଠିତ ହେବ ।
ଉତ୍ତଳ ଦର୍ପଣରେ ପ୍ରତିବିମ୍ବ ଗଠନ ସମ୍ପର୍କରେ ଜାଣିବାପାଇଁ ବସ୍ତୁର ଦୁଇଟି ସ୍ଥିତି ବିଚାର କରାଯାଇଛି ।
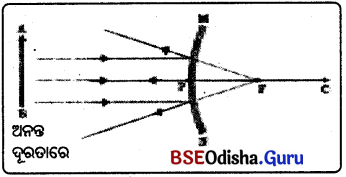
(a) ବସ୍ତୁ ଦର୍ପଣଠାରୁ ଅନନ୍ତ ଦୂରତାରେ ରହିଲେ
(i) ଅନନ୍ତ ଦୂରତାରେ ଥି AB ବସ୍ତୁର A ବିନ୍ଦୁରୁ ଆସୁଥିବା ଆଲୋକ ରଶ୍ମି ମୁଖ୍ୟ ଅକ୍ଷ ସହ ପ୍ରତିଫଳିତ ରଶ୍ମି ମୁଖ୍ୟ ଅକ୍ଷ ଠାରୁ ଦୂରେଇଯିବ ।
(ii) ପ୍ରତିଫଳିତ ରଶ୍ମି ଦର୍ପଣର ଅପର ପାର୍ଶ୍ଵରେ ଥିବା ଫୋକସ୍ ବିନ୍ଦୁରୁ ଆସିଲା ପରି ଜଣାପଡ଼ୁଛି ।
(iii) ସେହିପରି B ବିନ୍ଦୁରୁ ଆସୁଥିବା ଆଲୋକ ରଶ୍ମି ମୁଖ୍ୟ ଅକ୍ଷସହ ସମାନ୍ତର ହୋଇ ଆପତିତ ହୁଏ ଏବଂ ପ୍ରତିଫଳିତ ରଶ୍ମି ମୁଖ୍ୟ ଅକ୍ଷଠାରୁ ଦୂରେଇଯାଏ ।
(iv) ପ୍ରତିଫଳିତ ରଶ୍ମି ଦର୍ପଣର ଅପରପାର୍ଶ୍ଵରେ ଥିବା ଫୋକସ୍ ବିନ୍ଦୁରୁ ଆସିଲା ପରି ଜଣାପଡୁଛି ।
(v) ମୁଖ୍ୟ ଅକ୍ଷଦେଇ ଆସୁଥିବା ଆଲୋକ ରଶ୍ମି ଦର୍ପଣରେ ଆପତିତ ହେଲେ ମୁଖ୍ୟ ଅକ୍ଷଦେଇ ଫେରିଆସେ ।
(vi) ପ୍ରତିଫଳିତ ରଶ୍ମିଗୁଡ଼ିକୁ ବିପରୀତ ଦିଗରେ ବର୍ଷିତ କଲେ ତାହା ଉତ୍ତଳ ଦର୍ପଣର ଅପର ପାର୍ଶ୍ଵ F ଠାରେ ମିଳିତ ହେବ ଅର୍ଥାତ୍ F ଠାରୁ ବାହାରିବା ଭଳି ଜଣାପଡ଼ିବ ।
ପ୍ରତିବିମ୍ବର ଅବସ୍ଥିତି : ଦର୍ପଣର ପଛପଟେ ଫୋକସ୍ ବିନ୍ଦୁ (F) ଠାରେ ପ୍ରତିବିମ୍ବ ଗଠିତ ହେବ ।
ପ୍ରତିବିମ୍ବର ଆକାର ଓ ପ୍ରକୃତି : ପ୍ରତିବିମ୍ବର ଆକାର ଅତ୍ୟନ୍ତ କ୍ଷୁଦ୍ର ବିନ୍ଦୁ ସମ ହେବ । ପ୍ରତିବିମ୍ବ ଆଭାସୀ ଓ ସଳଖ ହେବ ।
(b) ବସ୍ତୁ ଦର୍ପଣ ନିକଟରେ ଏକ ପରିମିତ ଦୂରତାରେ ରହିଲେ (ଅନନ୍ତ ବିନ୍ଦୁ ଓ ପୋଲ୍ ମଧ୍ଯରେ ବସ୍ତୁ ଥିଲେ)
(i) ଉତ୍ତଳ ଦର୍ପଣ ସମ୍ମୁଖରେ ଥିବା AB ବସ୍ତୁର A ବିନ୍ଦୁରୁ ମୁଖ୍ୟ ଅକ୍ଷସହ ସମାନ୍ତର ଆଲୋକ ରଶ୍ମି D ବିନ୍ଦୁରେ ପ୍ରତିଫଳିତ ହୋଇ ମୁଖ୍ୟଅକ୍ଷଠାରୁ ଦୂରେଇ ଯାଇଛି।
(ii) DE ଫୋକସ୍ ଆସିଲା ଭଳି ଜଣାଯାଉଛି ।
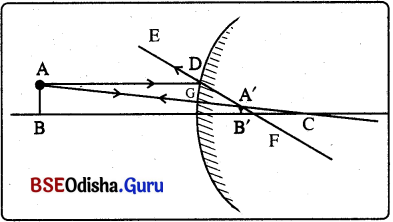
(iii) A ରୁ C ମଧ୍ୟଦେଇ ଯିବାଭଳି ଦେଖାଯାଇଥିବା AG ଆପତିତ ରଶ୍ମି GA ଦିଗରେ ପ୍ରତିଫଳିତ ହୋଇଛି ।
(iv) DE ଓ GA ପ୍ରତିଫଳିତ ରଶ୍ମିଦ୍ବୟ ଦର୍ପଣ ଆଗରେ ପରସ୍ପରକୁ ଛେଦ କରୁ ନାହାନ୍ତି । କିନ୍ତୁ ବିପରୀତ ଦିଗରେ ବଢ଼ାଇଲେ ଏଗୁଡ଼ିକ A’ ବିନ୍ଦୁରେ ମିଳିତ ହେଲାପରି ଜଣାପଡୁଛି ।
(v) A ବିନ୍ଦୁର ପ୍ରତିବିମ୍ବ A’ ଠାରେ ସୃଷ୍ଟିହୋଇଛି । ସେହିପରି ABର ପ୍ରତ୍ୟେକ ବିନ୍ଦୁର ପ୍ରତିବିମ୍ବ A’B’ ଠାରେ ସୃଷ୍ଟି ହୋଇଛି ।
ପ୍ରତିବିମ୍ବର ଅବସ୍ଥିତି : ଦର୍ପଣର ପଛପଟେ P ଓ F ମଧ୍ୟରେ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୋଇଛି ।
ପ୍ରତିବିମ୍ବର ଆକାର ଓ ପ୍ରକୃତି : ପ୍ରତିବିମ୍ବଟି ଆଭାସୀ, ସଳଖ ଓ ବସ୍ତୁ ତୁଳନାରେ ସାନ ହୋଇଛି ।
କାର୍ଯ୍ୟାବଳୀ- 6 (Activity-6)
ସମତଳ ଦର୍ପଣ, ଅବତଳ ଦର୍ପଣ ଓ ଉତ୍ତଳ ଦର୍ପଣରେ ଗଠିତ ହୋଇଥିବା ପ୍ରତିବିମ୍ବର ତୁଳନା କଲେ ଏଥ୍ ମଧ୍ୟରୁ କେଉଁ ଦର୍ପଣରେ ଗୋଟିଏ ବଡ଼ ବସ୍ତୁର ପୂର୍ବ ପ୍ରତିବିମ୍ବ ଦେଖହେବ !
ଆବଶ୍ୟକ ଉପକରଣ :
ଗୋଟିଏ ଲେଖାଏଁ ଅବତଳ ଦର୍ପଣ ଓ ଉତ୍ତଳ ଦର୍ପଣ, ବିଭିନ୍ନ ଦୈର୍ଘ୍ୟର ସମତଳ ଦର୍ପଣ ନିଅ ।
ପରୀକ୍ଷଣ :
- କୌଣସି ଏକ ଦୂରବସ୍ତୁ ଯଥା : ଦୂରରେ ଥିବା ଗୋଟିଏ ଗଛର ପ୍ରତିବିମ୍ବକୁ ସମତଳ ଦର୍ପଣରେ ଦେଖ !
- ତୁମେ କ’ଣ ପୂର୍ଣ୍ଣ ପ୍ରତିବିମ୍ବ ଦେଖ୍ ପାରିଲ କି ?
- ଭିନ୍ନ ଭିନ୍ନ ଆକାରର ସମତଳ ଦର୍ପଣ ବ୍ୟବହାର କର । ସମ୍ପୂର୍ଣ ବସ୍ତୁକୁ ପ୍ରତିବିମ୍ବରେ ଦେଖ୍ ପାରିଲ କି ?
- ଅବତଳ ଦର୍ପଣରେ ବ୍ୟବହାର କରି ପୂର୍ବପରି ଦେଖ୍ ଅବତଳ ଦର୍ପଣରେ ବସ୍ତୁର ପୂର୍ଣ୍ଣ ପ୍ରତିବିମ୍ବ ଦେଖ୍ ପାରିଲ କି ?
- ଉତ୍ତଳ ଦର୍ପଣ ବ୍ୟବହାର କରି ଏହି କାର୍ଯ୍ୟକୁ ଆଉଥରେ କର ।
ପର୍ଯ୍ୟବେକ୍ଷଣ ଓ ସିଦ୍ଧାନ୍ତ :
- ନାଁ ପୂର୍ଣ୍ଣ ପ୍ରତିବିମ୍ବ ଦେଖୁପାରିଲୁ ନାହିଁ ।
- ସମତଳ ଦର୍ପଣରେ ଗଛର କିଛି ଅଂଶର ପ୍ରତିବିମ୍ବ ଦେଖାଗଲା ।
- ଦୂରବସ୍ତୁର (ଗଛ) ର ଉଚ୍ଚତାର ଅଧା ଉଚ୍ଚତା ବିଶିଷ୍ଟ ସମତଳ ଦର୍ପଣ ନେବାରୁ ବସ୍ତୁର (ଗଛ)ର ସମ୍ପୂର୍ଣ୍ଣ ପ୍ରତିବିମ୍ବ ଦେଖୁରିଲୁ । ପ୍ରତିବିମ୍ବ ଦେଖିବାକୁ ହେଲେ ଦର୍ପଣକୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଉଚ୍ଚତାରେ ରଖିବା ଉଚିତ୍ ।
- ହଁ, ଅବତଳ ଦର୍ପଣ ବ୍ୟବହାର କରି ବସ୍ତୁର ପୂର୍ଣ୍ଣ ପ୍ରତିବିମ୍ବ ଦେଖ୍ ପାରିଲୁ । କାରଣ ସର୍ବଦା ଅବତଳ ଦର୍ପଣରେ ଦୂରବସ୍ତୁର ଓଲଟା ଓ ସାନ ପ୍ରତିବିମ୍ବ ଦେଖାଯାଏ, ତେଣୁ ଦୂର ଗଛର ସମ୍ପୂର୍ଣ୍ଣ ପ୍ରତିବିମ୍ବ ଦେଖ୍ ପାରିଲୁ ।
- ଉତ୍ତଳ ଦର୍ପଣ ଦ୍ବାରା ଦୂର ଗଛର ସମ୍ପୂର୍ଣ୍ଣ ପ୍ରତିବିମ୍ବ ଦେଖପାରିଲୁ କାରଣ ସର୍ବଦା ଉତ୍ତଳ ଦର୍ପଣରେ ଦୂର ବସ୍ତୁର ସଳଖ, କ୍ଷୁଦ୍ର ଆଭାସୀ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ।
ଉତ୍ତଳ ଦର୍ପଣର ବ୍ୟବହାର:
(a) ଯାନବାହାନରେ ଉତ୍ତଳ ଦର୍ପଣ ସାଧାରଣତଃ ପଛପାଖ (Rear-View) ଦେଖିବା ପାଇଁ ବ୍ୟବହାର କରାଯାଏ । ଚାଳକ ପଛରୁ ଆସୁଥୁବା ଗାଡ଼ିଗୁଡ଼ିକୁ ଦେଖାରେ ଓ ନିରାପଦ ଭାବରେ ଗାଡ଼ି ଚଳାଏ କାରଣ ଉତ୍ତଳ ଦର୍ପଣରେ ବସ୍ତୁଗୁଡ଼ିକର ସର୍ବଦା ସଳଖ, ସାନ ପ୍ରତିବିମ୍ବ ଦେଖହୁଏ ଏବଂ ସମତଳ ଦର୍ପଣ ଅପେକ୍ଷା ଅଧିକ ଅଞ୍ଚଳର ପ୍ରତିବିମ୍ବକୁ ଉତ୍ତଳ ଦର୍ପଣରେ ଦେଖ୍ହୁଏ ।
(b) ରାସ୍ତାକଡ଼ରେ ଜଳୁଥିବା ବିଦ୍ୟୁତ୍ ଖୁଣ୍ଟରେ ଆଲୋକ ପ୍ରତିଫଳକ ରୂପେ ଉତ୍ତଳ ଦର୍ପଣ ବ୍ୟବହାର ହୁଏ ।
![]()
କାର୍ଯ୍ୟାବଳୀ- 7 (Activity – 7)
ଗୋଟିଏ ଜଳଭର୍ତ୍ତିଥିବା ବାଲ୍ଟିରେ ମୁଦ୍ରା (ଟଙ୍କା) ର ଅବସ୍ଥାନ ।
ଆବଶ୍ୟକ ଉପକରଣ : ଜଳଭରିଥିବା ବାଲଟି, ଗୋଟିଏ ଟଙ୍କା ।
ପରୀକ୍ଷଣ :
ମୁଦ୍ରା (ଟଙ୍କା)କୁ ଜଳପୂର୍ଣ୍ଣ ବାଲ୍ଟିଟିରେ ପକାଅ । ଜଳସ୍ତର ଉପରେ ଗୋଟିଏ କଡ଼କୁ ଆଖୁରଖ୍ ଜଳରେ ହାତବୁଡ଼ାଇ ସେହି ଟଙ୍କାକୁ ଗୋଟିଏ ପ୍ରଚେଷ୍ଟାରେ ଉପରକୁ ଆଣିବା ପାଇଁ ଚେଷ୍ଟାକର ।
ଏହି କାମଟିକୁ ବାରମ୍ବାର କର ।
ତୁମ ସାଙ୍ଗମାନଙ୍କୁ ଏହି କାମ କରିବାକୁ ଦିଅ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ :
ଜଳ ପୃଷ୍ଠରୁ ଦେଖିଲେ ମୁଦ୍ରାଟି ଯେଉଁଠି ଅଛି ସେ ପର୍ଯ୍ୟନ୍ତ ହାତ ବୁଡ଼େଇ ଟଙ୍କା ଆଣିବାକୁ ଚେଷ୍ଟା କଲେ ମଧ୍ୟ ମୁଦ୍ରାଟିକୁ ଆଣି ହେଉନାହିଁ ।
ସିଦ୍ଧାନ୍ତ :
ଜଳରୁ ବାୟୁକୁ ଆଲୋକର ପ୍ରତିସରଣ ଯୋଗୁଁ ଟଙ୍କାଟି ଯେଉଁ ଅବସ୍ଥାନରେ ଅଛି ତା’ଠାରୁ କିଛି ଉପରକୁ ଥିଲା ଭଳି ଜଣାଯାଉଛି । ତେଣୁ ଜଣେ ଦେଖାଯାଉଥିବା ସ୍ଥାନରୁ ଟଙ୍କା ଆଣିପାରିଲା ନାହିଁ ।
କାର୍ଯ୍ୟାବଳୀ- 8 (Activity – 8)
ଜଳରେ ଆଲୋକର ପ୍ରତିସରଣ ଯୋଗୁଁ ମୁଦ୍ରାର ଆଭାସୀ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି କିମ୍ବା ମୁଦ୍ରାର ଅବସ୍ଥାନ ।
ଆବଶ୍ୟକ ଉପକରଣ :
ଏକ ଅଳ୍ପ ଗଭୀର ପାତ୍ର ବା କୁଣ୍ଡ, ଏକ ମୁଦ୍ରା, ଗୋଟିଏ ଟେବୁଲ, ଏକ ପାତ୍ରରେ କିଛି ପାଣି ।
ପରୀକ୍ଷଣ :
- ଗୋଟିଏ ଅଗଭୀର ପାତ୍ର ବା କୁଣ୍ଡକୁ ଟେବୁଲ ଉପରେ ରଖ୍ ତା’ ମଧ୍ୟରେ ମୁଦ୍ରାଟିଏ ରଖ ।
- ସେହି କୁଣ୍ଡ ପାଖରୁ ଧୀରେ ଧୀରେ ଦୂରେଇଯାଅ ଯେଉଁ ସ୍ଥାନରେ ତୁମେ ଟଙ୍କାଟିଏ ଆଉ ଦେଖାରିବ ନାହିଁ ସେଠାରେ ସ୍ଥିର ହୋଇଯାଅ ।
- ତୁମ ସାଙ୍ଗକୁ କୁହ ସେହି ଟଙ୍କାଟିକୁ କୁଆଡ଼େ ନ ଘୁଞ୍ଚାଇ ସେ କୁଣ୍ଡରେ ଧୀରେ ଧୀରେ ଜଳ ଭର୍ତ୍ତିକରିବ ।
- ଜଳ ଭର୍ତି ହେଉଥିଲାବେଳେ ଟଙ୍କାଟିଏ ଦେଖିବାକୁ ଲକ୍ଷ୍ୟ ରଖୁଥାଅ । ପର୍ଯ୍ୟବେକ୍ଷଣ :
ପର୍ଯ୍ୟବେକ୍ଷଣ :
ପାତ୍ରରେ ପାଣିଢାଳିବାରୁ ପାଣିରେ ବୁଡ଼ିଥିବା ମୁଦ୍ରାଟି ପୁନର୍ବାର ଦେଖାଗଲା ।
ସିଦ୍ଧାନ୍ତ :
ପାଣି ପୂର୍ଣ୍ଣହେବା ପୂର୍ବରୁ ମୁଦ୍ରାରୁ ଆସୁଥିବା ଆଲୋକ ରଶ୍ମି ପାତ୍ରର ଧାରଦ୍ଵାରା ବାଧା ପାଉଥିବାରୁ ମୁଦ୍ରାଟି ତୁମକୁ ଦେଖାଯାଉନଥିଲା । ପାଣି ପୂର୍ଣ୍ଣହେବାପରେ ମୁଦ୍ରାରୁ ଆସୁଥିବା ଆଲୋକ ରଶ୍ମି ପାଣି ମଧ୍ୟଦେଇ ଗତିକରି ବାୟୁକୁ ଆସିବାବେଳେ ଅଭିଲମ୍ବଠାରୁ ଦୂରେଇଯିବାରୁ ମୁଦ୍ରାଟି ଦେଖାଗଲା । ଆଲୋକର ପ୍ରତିସରଣ ଯୋଗୁଁ ମୁଦ୍ରାଟି ତା’ର ପ୍ରକୃତ ସ୍ଥାନ ଠାରୁ ଉପରକୁ ଉଠିଥିଲା ପରି ଜଣାପଡୁଛି ।
କାର୍ଯ୍ୟାବଳୀ- 9 (Activity – 9)
ପ୍ରତିସରଣ ଯୋଗୁଁ କାଚଦ୍ବାରା ସରଳରେଖାର ବଙ୍କା ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହୁଏ ।
ଆବଶ୍ୟକ ଉପକରଣ :
ଗୋଟିଏ ଧଳା କାଗଜ, ଏକ କାଚସ୍ଲାବ୍, କାଳି କଲମ, ଟେବୁଲ ।
ପରୀକ୍ଷଣ :
- ଟେବୁଲ ଉପରେ ଧଳା କାଗଜ ରଖ୍ ତା’ ଉପରେ କାଳିରେ ଏକ ମୋଟା ସଳଖ ରେଖା ଟାଣ ।
- କାଚର ସ୍ଲାବ୍କୁ ଏହି ରେଖା ଉପରେ ଏପରି ରଖ ଯେମିତି ସ୍ଲାବ୍ର ଗୋଟିଏ ଧାର ସେହି ରେଖା ସହିତ ଏକ କୋଣ କରିବ ।
- ଗୋଟିଏ କଡ଼ରୁ ସ୍କାଚ୍ ତଳେ ରହିଥିବା ରେଖାକୁ ଲକ୍ଷ୍ୟ କର । ସ୍ଲାବ୍ର ଧାର ନିକଟରେ ରେଖାଟି ବଙ୍କା
- ଏହାପରେ ସ୍ଲାବ୍କୁ ବୁଲେଇ ରେଖା ଉପରେ ଏମିତି ରଖ ଯେମିତି ସ୍ଲାବର ଧାର ରେଖା ପ୍ରତି ଅଭିଲମ୍ବ ହେବ । ସ୍ଲାବ୍ରତଳେ ରହିଥିବା ରେଖାଶ କ’ଣ ବାଙ୍କିଗଲା ପରି ଜଣାପଡୁଛି ?
- ସ୍ଲାବ୍ ଉପରୁ ସ୍କାଚ୍ ତଳେ ଥିବା ରେଖାକୁ ଲକ୍ଷ୍ୟକର । ସ୍ଲାବ୍ ତଳେ ରହିଥିବା ରେଖାଶ ଟିକେ ଉପରକୁ ଉଠିଲା ଭଳି ଲାଗୁଛି କି ?
ପର୍ଯ୍ୟବେକ୍ଷଣ :
- ହଁ, କାଚ ପ୍ଳାବତଳେ ରହିଥିବା ରେଖା ବଙ୍କା ଭଳି ଦେଖାଯାଉଛି କାରଣ ଆଲେକର ପ୍ରତିସରଣ ଯୋଗୁଁ ଏଭଳି ହୋଇଛି ।
- ନାଁ, ରେଖାର ଏକ ଅଂଶ ବଙ୍କା ଦେଖାଯାଉ ନାହିଁ କାରଣ ଆଲୋକ ରଶ୍ମି କାଚ ସ୍ଲାବ୍ ଓ ବାୟୁର ବ୍ୟବଧାନ ପୃଷ୍ଠରେ ସାଧାରଣତଃ ଆପତିତ ହୋଇଛି କିନ୍ତୁ ପ୍ରତିସୃତ ହୋଇନାହିଁ ।
- ହଁ, କାଚ ସ୍କାବ୍ର ତଳେ ଥିବା ରେଖାର କିଛିଅଂଶ ଉପରକୁ ଉଠିଲାଭଳି ଲାଗୁଛି । କାରଣ ଆଲୋକ ରଶ୍ମି କାଚ ସ୍କାଚ୍ରୁ ବାୟୁକୁ ପ୍ରତିସୃତ ହେବା ଯୋଗୁଁ ଏଭଳି ହୁଏ ।
![]()
କାର୍ଯ୍ୟାବଳୀ- 10 (Activity – 10)
ଆବଶ୍ୟକ ଉପକରଣ :
ଏକ ଧଳାକାଗଜ ଫର୍ଦ, ଡ୍ରଇଁପଟା, ଡ୍ରଇଁପିନ୍, ଚାରୋଟି ଆଲପିନ୍, ମୁନିଆ ପେନସିଲ୍, ସ୍କେଲ୍ ।
ପରୀକ୍ଷଣ :
(i) ଡ୍ରଇଁ ପିନଦ୍ୱାରା ଧଳାକାଗଜ ଫର୍ଦ୍ଦକୁ ଡ୍ରଇଁ ପଟା ଉପରେ ଲଗାଯାଉ ।
(ii) ଗୋଟିଏ ଆୟତଘନାକାର କାଚ ସ୍କାକୁ କାଗଜ ମଝିରେ ରଖାଯାଉ ।
(iii) ସ୍ଲାବ୍ର ବାହ୍ୟ ସୀମାରେଖା (Outline)କୁ ପେନ୍ସିଲ୍ ସାହାଯ୍ୟରେ ଅଙ୍କନ କରି ତାହାର ନାମ ABCD ଦିଆଯାଉ ।
(iv) ଅଗ୍ରଭାଗ ମୁନିଆ ଥିବା 4ଟି ସମାନ ଡେଙ୍ଗା ପିନ୍ ନିଆଯାଉ ।
(v) କାଗଜ ଉପରେ E ଓ F ନାମକ ଦୁଇଟି ପିନ୍ ଭୂଲମ୍ବ ଭାବରେ ପୋତ ଯେମିତି E ଓ F ର ମୁନକୁ ଯୋଗ କଟୁଥିବା ରେଖା ସ୍ଲାବ୍ର AB ଧାର ପ୍ରତି ତୀର୍ଯ୍ୟକ ହେବ ।
(vi) E ଓ F ପିଦ୍ଵୟ ସ୍ଲାବ୍ର ଯେଉଁ ପାର୍ଶ୍ବରେ ପୋତାଯାଇଛି, ତା’ର ଅପର ପାର୍ଶ୍ଵରେ G ଓ H ନାମକ ଆଉ ଦୁଇଟି ପିନ୍ କାଗଜ ଉପରେ ଭୂଲମ୍ବ ଭାବରେ ଏପରି ପୋତ ଯେପରିକି E ଓ F ପିୟର ମୂଳର ପ୍ରତିବିମ୍ବ
G ଓ H ପିନର ମୂଳଦ୍ଵୟ ଗୋଟିଏ ସରଳରେଖାରେ ରହିବେ ।
(vii) କାଗଜ ଉପରୁ ସବୁ ପିନ୍ ଓ ପ୍ଲାକୁ କାଢ଼ି ଦିଆଯାଉ ।
(viii) E ଓ F ପିନ୍ ର ସ୍ଥିତି ସୂଚିତ କରୁଥିବା ବିନ୍ଦୁକୁ କାଗଜ ଉପରେ ଯୋଗ କରି ସରଳରେଖା ଅଙ୍କନ କଲେ ତାହା AB ଧାରକୁ ( ବିନ୍ଦୁରେ ସ୍ପର୍ଶକରିବ । ସେହିପରି G ଓ H ପିନ୍ର ସ୍ଥିତି ସୂଚିତ କରୁଥିବା ବିନ୍ଦୁ ଦୁଇଟିକୁ ଯୋଗ କରି ସରଳରେଖା ଅଙ୍କନ କଲେ ତାହା CD ଧାରକୁ ଠା’ ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରିବ ।
(ix) O ଓ ଠ’ କୁ କାଗଜ ଉପରେ ଯୋଗ କର । EF କୁ F ଦିଗରେ P ବିନ୍ଦୁ ପର୍ଯ୍ୟନ୍ତ ବିନ୍ଦୁ କି ତ (dotted) ରେଖାଦ୍ଵାରା ବଦ୍ଧିତ କରାଯାଇଛି । ଠ ଓ ୦’କୁ ଦୁଇଟି ବ୍ୟବଧାନ ପୃଷ୍ଠ ଉପରେ ଅଛି ।
(x) O ବିନ୍ଦୁରେ ସ୍କାଚ୍ AB ପୃଷ୍ଠ ପ୍ରତି ଏବଂ O’ ବିନ୍ଦୁରେ CD ପୃଷ୍ଠ ପ୍ରତି ଯଥାକ୍ରମେ NN’ ଓ MM’ ଅଭିଲମ୍ବ
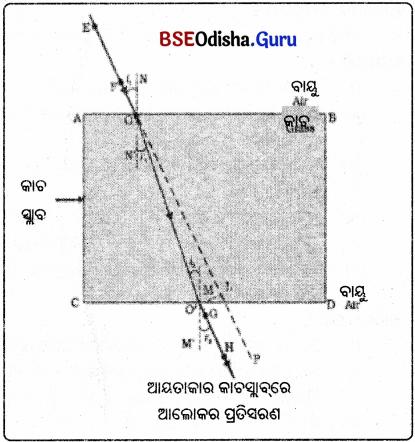
ପର୍ଯ୍ୟବେକ୍ଷଣ :
(i) O ଓ O’ ବିନ୍ଦୁରେ ଆଲୋକ ତା’ର ଗତିପଥରେ ଦିଗ ପରିବର୍ତ୍ତନ କରିଛି । କାରଣ ଆଲୋକ ରଶ୍ମି ଠ ବିନ୍ଦୁଠାରେ ବାୟୁରୁ କାଚ ମାଧ୍ୟମକୁ ଅର୍ଥାତ୍ ଏକ ଲଘୁ ମାଧ୍ୟମରୁ ଘନ ମାଧ୍ୟମକୁ ପ୍ରବେଶ କରିଛି । O ବିନ୍ଦୁରେ ଆଲୋକ ରଶ୍ମି ଅଭିଲମ୍ବ ଆଡ଼କୁ ବଙ୍କେଇ ଯାଇଛି ।
(iii) ପ୍ରତିସରଣ କୋଣ ଆପତନ କୋଣଠାରୁ କମ୍ ହୋଇଛି ଅର୍ଥାତ୍ ∠r2 < ∠r1
(iv) ଆଲୋକ ରଶ୍ମି ୦’ ବିନ୍ଦୁଠାରେ କାଚ ମାଧ୍ୟମରୁ ବାୟୁ ମାଧ୍ୟମକୁ ଅର୍ଥାତ୍ ଘନ ମାଧ୍ୟମରୁ ଲଘୁ ମାଧ୍ୟମକୁ ପ୍ରବେଶ କରିଛି । (‘ ବିନ୍ଦୁଠାରେ ଆଲୋକ ରଶ୍ମି ଅଭିଲମ୍ବଠାରୁ ଦୂରକୁ ବାଙ୍କିଯାଇଛି ।
(v) ପ୍ରତିସରଣ କୋଣ, ଆପତନ କୋଣଠାରୁ ଅଧିକ ଅର୍ଥାତ୍ ∠r2 > ∠r1 ।
ସିଦ୍ଧାନ୍ତ :
EO ହେଉଛି ଆପତିତ ରଶ୍ମି, ୦୦’ ହେଉଛି ପ୍ରତିସୃତ ରଶ୍ମି ଓ O’H ହେଉଛି ନିର୍ଗତ (Emergent) ରଶ୍ମି । ନିର୍ଗତ ରଶ୍ମି O’H, ଆପତିତ ରଶ୍ମିର ଦିଗ ସହିତ ସମାନ୍ତର । ଆୟତାକାର କାଚ କ୍ଲବ୍ର ଦୁଇଟି ବିପରୀତ ସମାନ୍ତର ପୃଷ୍ଠ AB ଓ CDରେ ଆଲୋକ ରଶ୍ମି ବାଙ୍କିଯିବାର ପରିମାଣ ସମାନ ଓ ବିପରୀତ । ଏହି କାରଣରୁ ନିର୍ଗତ ବିନ୍ଦୁଠାରେ ଆଲୋକ ରଶ୍ମି ଆପତିତ ରଶ୍ମି ସହିତ ସମାନ୍ତର ହୋଇ ନିର୍ଗତ ହୁଏ । ମାତ୍ର ଗୋଟିଏ କଡ଼କୁ ବିସ୍ଥାପିତ ହୋଇଥାଏ । ଏହାକୁ ପାର୍ଶ୍ଵ ବିସ୍ଥାପନ (Lateral Displacement) କହନ୍ତି ।
ଆଲୋକ ରଶ୍ମି ଦୁଇଟି ସ୍ଵଚ୍ଛ ମାଧ୍ୟମର ବ୍ୟବଧାନ ପୃଷ୍ଠରେ ଅଭିଲମ୍ବ ଭାବରେ ପଡ଼ିଲେ i = 0) ହେବ, ତେବେ ନିର୍ଗତ ରଶ୍ମି ନିର୍ଗମନ ପୃଷ୍ଠ ପ୍ରତି ଲମ୍ବ ହେବ ଓ 1 = 0 ହେବ । ଫଳରେ EO, ୦୦’ ଓ O’H ଗୋଟିଏ ସରଳରେଖାରେ ରହିବେ ଏବଂ ପାର୍ଶ୍ଵ ପରିବର୍ତ୍ତନର ପରିମାଣ ଶୂନ ହେବ ।
ପ୍ରତିସରଣ ଜନିତ ପାର୍ଶ୍ଵବିସ୍ଥାପନର ପରିମାଣ (i) କାଚଖଣ୍ଡର ମୋଟେଇ, (ii) ଆପତନ କୋଣ ଓ (iii) ପ୍ରତିସରଣ କୋଣ ଉପରେ ନିର୍ଭର କରେ ।
ପ୍ରତିସରଣର ନିୟମ (Laws of Refraction):
(i) ଆପତିତ ରଶ୍ମି, ପ୍ରତିସୃତ ରଶ୍ମି ଓ ଆପତନ ବିନ୍ଦୁଠାରେ ଦୁଇଟି ସ୍ଵଚ୍ଛ ମାଧ୍ୟମର ବ୍ୟବଧାନ ପୃଷ୍ଠ ପ୍ରତି ଅଙ୍କିତ ଅଭିଲମ୍ବ ଗୋଟିଏ ସମତଳରେ ରହେ ।
(ii) ଦୁଇଟି ନିର୍ଦ୍ଦିଷ୍ଟ ମାଧ୍ୟମ ଓ ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ବଣ୍ଟର ଆଲୋକ ପାଇଁ ଆପତନ କୋଣର ସାଇନ୍ (Sine) ଓ ପ୍ରତିସରଣ କୋଣର ସାଇନ (Sine)ର ଅନୁପାତ ଏକ ସ୍ଥିରାଙ୍କ ।
ଏହି ସ୍ଥିରାଙ୍କର ମୂଲ୍ୟ ମାଧ୍ୟମ ଦ୍ଵୟର ପ୍ରକୃତି ଓ ଆଲୋକର ବର୍ଣ୍ଣ ଉପରେ ନିର୍ଭର କରେ । ଏହି ନିୟମକୁ ସ୍କେଲଙ୍କ ପ୍ରତିସରଣ ନିୟମ କୁହାଯାଏ ।
ଯଦି ଆପତନ କୋଣ ‘i’ ହୁଏ ଓ ପ୍ରତିସରଣ କୋଣ ‘r’ ହୁଏ ତେବେ \(\frac { sin i }{ sin r }\) = ସ୍ଥିରାଙ୍କ
ଏହି ସ୍ଥିରାଙ୍କକୁ ପ୍ରଥମ ମାଧ୍ୟମ ତୁଳନାରେ ଦ୍ଵିତୀୟ ମାଧ୍ୟମର ପ୍ରତିସରଣାଙ୍କ (Refractive Index) କୁହାଯାଏ ।
ପ୍ରତିସରଣାଙ୍କ (Refractive Index) :
ଶୂନ୍ୟ (ବାୟୁ) ମାଧ୍ୟମରେ ଆଲୋକର ବେଗ ଏବଂ ଅନ୍ୟ ଯେକୌଣସି ମାଧ୍ୟମରେ ଆଲୋକର ବେଗର ଅନୁପାତକୁ ମାଧ୍ୟମର ପ୍ରତିସରଣାଙ୍କ କୁହାଯାଏ ।
ଅର୍ଥାତ୍ \(\frac { sin i }{ sin r }\) = ସ୍ଥିରାଙ୍କ ।
ଅର୍ଥାତ୍ ଆପତନ କୋଣ i ଓ ପ୍ରତିସରଣ କୋଣ r ହେଲେ ସ୍କେଲ୍ଙ୍କ ନିୟମ ଅନୁସାରେ \(\frac { sin i }{ sin r }\) = ଏକ
ସ୍ଥିରାଙ୍କ । ଏହି ସ୍ଥିରାଙ୍କକୁ ପ୍ରଥମ ମଧ୍ୟମ ତୁଳନାରେ ଦ୍ଵିତୀୟ ମାଧ୍ୟମର ପ୍ରତିସରଣାଙ୍କ କୁହାଯାଏ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ :
(i) ଯଦି ଆଲୋକରଶ୍ମି କାଚ ମଧ୍ୟରେ ପ୍ରବେଶ କରେ ତେବେ \(\frac { sin i }{ sin r }\) କୁ ବାୟୁ ତୁଳନାରେ କାଚର ପ୍ରତିସରଣାଙ୍କ କୁହାଯାଏ ।
∴ \(\frac { sin i }{ sin r }\) = μ କାଚ |
(ii) ଯଦି ଆଲୋକ ରଶ୍ମି ଶୂନ୍ୟରୁ କାଚ ମଧ୍ୟରେ ପ୍ରବେଶ କରେ, ତେବେ \(\frac { sin i }{ sin r }\) କୁ ଶୂନ୍ୟ ତୁଳନାରେ କାଚର ପ୍ରତିସରଣାଙ୍କ କୁହାଯାଏ ।
∴ \(\frac { sin i }{ sin r }\) = ବାୟୁ μ କାଚ ।
(iii) ଯଦି ଆଲୋକ ରଶ୍ମି କାଚରୁ ବାୟୁ ମଧ୍ୟକୁ ପ୍ରବେଶ କରେ, ତେବେ \(\frac { sin i }{ sin r }\) କୁ କାଚ ତୁଳନାରେ ବାୟୁର ପ୍ରତିସରଣାଙ୍କ କୁହାଯାଏ ।
∴ \(\frac { sin i }{ sin r }\) = କାଚ μ ବାୟୁ ।
କାର୍ଯ୍ୟାବଳୀ- 11 (Activity – 11)
ଉତ୍ତଳ ଲେନସର ଆସନ୍ନ ଫୋକସ୍ ଦୂରତା ନିର୍ଣ୍ଣୟ :
ଆବଶ୍ୟକ ଉପକରଣ :
ଉତ୍ତଳ ଲେନସ୍, ଫର୍ଭେ କାଗଜ, ମିଟରସ୍କେଲ୍ ।
ସତର୍କତା :
ଏହି କାମ କଲାବେଳେ ସୂର୍ଯ୍ୟକୁ ସିଧା ବା ଲେନସ୍ ମଧ୍ୟଦେଇ ଆଦୌ ଅନାଇବ ନାହିଁ ।
ପରୀକ୍ଷଣ :
- ଏକ ଉତ୍ତଳ ଲେନ୍ସକୁ ହାତରେ ଧରି ସୂର୍ଯ୍ୟଆଡ଼କୁ ରଖ ।
- ସୂର୍ଯ୍ୟରୁ ଆସୁଥିବା ଆଲୋକକୁ ଏକ କାଗଜ ଉପରେ ଫୋକସ୍ (କେନ୍ଦ୍ରୀଭୂତ) କରାଅ । ଏହାଦ୍ୱାରା ସୂର୍ଯ୍ୟର ଏକ ଉତ୍ତଳ ପ୍ରତିବିମ୍ବ ତୁମ କାଗଜ ଉପରେ ପକାଅ ।
- ଲେନ୍ସ ଓ କାଗଜକୁ ହଲ୍ଚଲ୍ ନ କରି ସେହି ଅବସ୍ଥାରେ ରଖ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ :
(i) କିଛି ମୁହୂର୍ତ୍ତ ମଧ୍ୟରେ କାଗଜଟିରୁ ଧୂଆଁ ବାହାରିବାକୁ ଆରମ୍ଭ କରିବ ।
(ii) ସୂର୍ଯ୍ୟାଲୋକ ସମାନ୍ତର ଆଲୋକ ଗୁଚ୍ଛ ଅଟେ । ଏହି ରଶ୍ମିଗୁଚ୍ଛ ଲେନ୍ସ ଓ କାଗଜକୁ ହଲ୍ଚଲ୍ ନ କରି ସେହି ଅବସ୍ଥାରେ ରଖ । ପଡ଼ିଲା । ଏହାଯୋଗୁଁ କାଗଜ ଉପରେ ଏକ ତୀକ୍ଷ୍ଣ ଉଜ୍ଜ୍ଵଳ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହେଲା ।
ସିଦ୍ଧାନ୍ତ
ଏହି ଉଜ୍ଜ୍ଵଳ ପ୍ରତିବିମ୍ବ ସୂର୍ଯ୍ୟର ବାସ୍ତବ ପ୍ରତିବିମ୍ବ । ସୂର୍ଯ୍ୟାଲୋକ କାଗଜ ଉପରେ ଗୋଟିଏ ବିନ୍ଦୁରେ କେନ୍ଦ୍ରୀଭୂତ ହେବା ଫଳରେ ତାପମାତ୍ରା ବୃଦ୍ଧି ହୋଇ କାଗଜ ଜଳିଗଲା ।
ପ୍ରମୁଖ ଫୋକସ୍ ଉତ୍ତଳ ଲେନସ୍ର ଫୋକସ୍ :
(i) ଉତ୍ତଳ ଲେନସ୍ର ପ୍ରମୁଖ ଅକ୍ଷସହ ସମାନ୍ତର ଥିବା ଅନେକଗୁଡ଼ିଏ ଆପତିତ ହୋଇଥିବା ଆଲୋକ ରଶ୍ମି ପ୍ରତିସରଣ ପରେ ଲେନସ୍ର ଅପର ପାର୍ଶ୍ଵରେ ଅଭିସାରିତ ହୋଇ ପ୍ରମୁଖ ଅକ୍ଷ ଉପରେ ଗୋଟିଏ ବିନ୍ଦୁରେ ମିଳିତ ହୋଇଛି । ପ୍ରମୁଖ ଅକ୍ଷ ଉପରେ ଥିବା ଏହି ବିନ୍ଦୁକୁ ଲେନସ୍ର ପ୍ରମୁଖ ଫୋକସ୍ କୁହାଯାଏ ।
(ii) ଯଦି ସମାନ୍ତର ଆଲୋକ ରଶ୍ମିଗୁଡ଼ିକ ଲେନସ୍ର ବିପରୀତ ପାର୍ଶ୍ବରୁ ପ୍ରବେଶ କରାଇବ ତେବେ ବିପରୀତ ପାର୍ଶ୍ବରେ ଆଉ ଗୋଟିଏ ପ୍ରମୁଖ ଫୋକସ୍ ପାଇବ । ପ୍ରମୁଖ ଫୋକସ୍ ୮ ଅକ୍ଷରଦ୍ଵାରା ଚିହ୍ନିତ କରାଯାଏ ! ଲେନସ୍ର ଦୁଇଟି ପ୍ରମୁଖ ଫୋକସ୍ ଅଛି । ସେମାନଙ୍କୁ F1 ଓ F2 ଅକ୍ଷର ଦ୍ବାରା ଚିହ୍ନିତ କରାଯାଏ ।
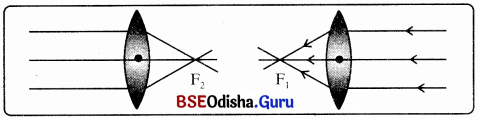
ଅବତଳ ଲେନସ୍ର ଫୋକସ୍ :
ପ୍ରମୁଖ ଅକ୍ଷ ଉପରିସ୍ଥ ଗୋଟିଏ ବିନ୍ଦୁରୁ ଅପସାରିତ ହୋଇ ଆସିଲାପରି ଜଣା ପଡ଼େ । ପ୍ରମୁଖ ଅକ୍ଷ ଉପରେ ଏହି ବିନ୍ଦୁକୁ ଅବତଳ ଲେନସ୍ର ପ୍ରମୁଖ ଫୋକସ୍ କୁହାଯାଏ ।
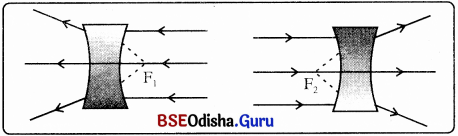
ଫୋକସ୍ ଦୂରତା :
ଲେନସ୍ର ଆଲୋକ କେନ୍ଦ୍ରଠାରୁ ଫୋକସ୍ ବିନ୍ଦୁ ପର୍ଯ୍ୟନ୍ତ ଦୂରତାକୁ ଫୋକସ୍ ଦୂରତା କୁହାଯାଏ । ଫୋକସ୍ ଦୂରତାକୁ ‘f’ ଅକ୍ଷ ଦ୍ଵାରା ଚିହ୍ନିତ କରାଯାଏ ।
![]()
କାର୍ଯ୍ୟାବଳୀ- 12 (Activity – 12)
ଉତ୍ତଳ ଲେନ୍ସଦ୍ବାରା ଗଠିତ ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି, ସ୍ଥିତି ଓ ଆପେକ୍ଷିକ ଆକାର ସମ୍ପର୍କରେ ଜାଣିବା ।
ଆବଶ୍ୟକ ଉପକରଣ :
ଗୋଟିଏ ଉତ୍ତଳ ଲେନସ୍ , ଏକ ମିଟର ସ୍କେଲ, ଜଳନ୍ତା ମହମବତୀ, ଏକ ଷ୍ଟାଣ୍ଡ, ଏକ ଟେବୁଲ୍ ଓ ଗୋଟିଏ ପରଦା ।
ପରୀକ୍ଷଣ :
(i) ଗୋଟିଏ ଉତ୍ତଳ ଲେନ୍ସ ନିଅ । ଏହା ପୂର୍ବରୁ ଥିବା ‘ତୁମ ପାଇଁ କାମ’ରେ ବର୍ଣ୍ଣନା କରାଯାଇଥିବା ଅନୁସାରେ ଲେନ୍ସର ଫୋକସ୍ ଦୂରତା ବାହାର କର ।
(ii) ଟେବୁଲ ଉପରେ 5ଟି ସମାନ୍ତର ରେଖା ଅଙ୍କନ କର । ପାଖାପାଖୁ ରହିଥିବା ଯେ କୌଣସି ଦୁଇଟି ରେଖା ମଧ୍ୟରେ ଦୂରତା, ଲେନ୍ସର ଫୋକସ୍ ଦୂରତା ସହିତ ସମାନ ହେବ ।
(iii) ଲେନ୍ସକୁ ଏକ ଷ୍ଟାଣ୍ଡ ସହିତ ସଂଯୁକ୍ତ କର । ଏହାକୁ ଟେବୁଲ ଉପରେ ଅଙ୍କିତ ରେଖାମାନଙ୍କର ମଧ୍ୟବର୍ତ୍ତୀ ରେଖା ଉପରେ ରଖ ଯେମିତି ଲେନ୍ସର ଆଲୋକ କେନ୍ଦ୍ର ଠିକ୍ ସେହି ରେଖା ଉପରେ ରହିବ ।
(iv) ଲେନ୍ସର ଦୁଇ ପଟରେ ଥିବା ପାଖାପାଖ୍ ଦୁଇଟି ରେଖାର ସ୍ଥିତି ଲେନ୍ସର F ଓ 2F ଅନୁରୂପୀ ହେବ । ସେମାନଙ୍କୁ ଉପଯୁକ୍ତ ଭାବରେ 2F1, F1 , 2F2 ଏବଂ F2 ଅକ୍ଷର ଦ୍ଵାରା ଚିହ୍ନିତ କର |
(v) ବାମପାର୍ଶ୍ବରେ 2F1 ଠାରୁ ବହୁତ ଦୂରରେ ଏକ ଜଳନ୍ତା ମହମବତୀ ରଖ। ଲେନ୍ସର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଗୋଟିଏ ପରଦା ଉପରେ ଏହାର ଏକ ସ୍ପଷ୍ଟ, ତୀକ୍ଷ୍ଣ ପ୍ରତିବିମ୍ବ ପାଇବା ।
(vi) ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି, ସ୍ଥିତି ଓ ଆପେକ୍ଷିକ ଆକାରକୁ ଲେଖୁ ରଖ ।
(vii) ଏହାପରେ ବସ୍ତୁ (ମହମବତୀ)କୁ 2F1 ଠାରୁ ସାମାନ୍ୟ ଦୂରରେ, F1 ଓ 2F1 ମଝିରେ F1 ଉପରେ ଏବଂ F1 ଓ O ମଝିରେ ରଖୁ ଉପରୋକ୍ତ କାର୍ଯ୍ୟକୁ ପୁନର୍ବାର କର । ବସ୍ତୁର ପ୍ରତ୍ୟେକ ସ୍ଥିତି ପାଇଁ ପ୍ରତିବିମ୍ବ ଦେଖ ଓ ତୁମର ପର୍ଯ୍ୟବେକ୍ଷଣକୁ ଲେଖୁ ରଖ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ :
ବସ୍ତୁର ଭିନ୍ନ ଭିନ୍ନ ସ୍ଥିତି ପାଇଁ ଉତ୍ତଳ ଲେନ୍ସରେ ସୃଷ୍ଟ ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି, ସ୍ଥିତି ଓ ଆପେକ୍ଷିକ ଆକାର
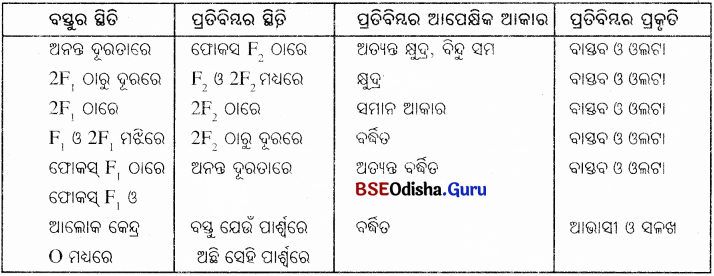
ସିଦ୍ଧାନ୍ତ :
ବସ୍ତୁର ସ୍ଥିତି ଅନୁସାରେ ପ୍ରତିବିମ୍ବର ସ୍ଥିତି, ଆପେକ୍ଷିକ ଆକାର ଓ ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି ବଦଳେ ।
କାର୍ଯ୍ୟାବଳୀ- 13 (Activity – 13)
ଅବତଳ ଲେନସ୍ଦ୍ୱାରା ସୃଷ୍ଟ ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି ସ୍ଥିତି ଓ ଆପେକ୍ଷିକ ଆକାର ସମ୍ପର୍କରେ ଜାଣିବା ।
ଆବଶ୍ୟକ ଉପକରଣ : ଅବତଳ ଲେନ୍ସ୍, ଜଳନ୍ତା ମହମବତୀ
ପରୀକ୍ଷଣ :
- ଗୋଟିଏ ଅବତଳ ଲେନ୍ସ ନିଅ । ଏହାକୁ ଏକ ଷ୍ଟାଣ୍ଡ ଉପରେ ଲଗାଅ ।
- ଗୋଟିଏ ଜଳନ୍ତା ମହମବତୀକୁ ଲେନ୍ସର ଗୋଟିଏ ପାର୍ଶ୍ଵରେ ରଖ ।
- ଅପର ପାର୍ଶ୍ଵରୁ ଲେନ୍ସ ଭିତରକୁ ଲକ୍ଷ୍ୟ କରି ପ୍ରତିବିମ୍ବ ଦେଖ ।
- ପ୍ରତିବିମ୍ବକୁ ଗୋଟିଏ ପରଦା ଉପରେ ପକାଇବା ପାଇଁ ଚେଷ୍ଟା କର । ନ ପଡ଼ିଲେ ଲେନ୍ସ ଭିତର ଦେଇ ପ୍ରତିବିମ୍ବକୁ ସିଧା ଦେଖ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ :
ବସ୍ତୁର ଭିନ୍ନ ଭିନ୍ନ ସ୍ଥିତି ପାଇଁ ଅବତଳ ଲେନ୍ସ ଦ୍ବାରା ସୃଷ୍ଟ ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି, ସ୍ଥିତି ଓ ଆପେକ୍ଷିକ ଆକାର
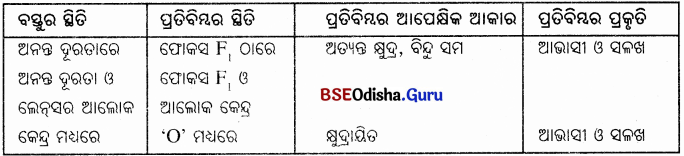
ମହମବତୀକୁ ଲେନସ୍ରୁ ଧୀରେ ଧୀରେ ଦୂରକୁ ଘୁଞ୍ଚାଇଲେ ପ୍ରତିବିମ୍ବର ଆକାର ହ୍ରାସପାଏ । ଯେତେବେଳେ ମହମବତୀ ଲେନସ୍ଠାରୁ ବହୁତ ଦୂରରେ ରହେ ପ୍ରତିବିମ୍ବ ଅତ୍ୟନ୍ତ କ୍ଷୁଦ୍ର ହୁଏ, ଏପରିକି ବିନ୍ଦୁଭଳି ହୋଇଯାଏ ।
ସିଦ୍ଧାନ୍ତ :
ବସ୍ତୁର ଯେକୌଣସି ଅବସ୍ଥିତି ପାଇଁ ଅବତଳ ଲେନସ୍ ସର୍ବଦା ଆଭାସୀ, ସଳଖ ଓ କ୍ଷୁଦ୍ର ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟିକରେ ।
