BSE Odisha 10th Class Physical Science Notes Chapter 6 ଆଲୋକ- ପ୍ରତିଫଳନ ଓ ପ୍ରତିସରଣ

Odisha State Board BSE Odisha 10th Class Physical Science Notes Chapter 6 ଆଲୋକ- ପ୍ରତିଫଳନ ଓ ପ୍ରତିସରଣ will enable students to study smartly.

BSE Odisha Class 10 Physical Science Notes Chapter 6 ଆଲୋକ- ପ୍ରତିଫଳନ ଓ ପ୍ରତିସରଣ

→ ଉପକ୍ରମ (Introduction) :

• ଆଲୋକ ଏକ ପ୍ରକାରର ଶକ୍ତି ଯାହା ଆମେ ଚକ୍ଷୁ ମାଧ୍ୟମରେ ଅନୁଭବ କରୁ ।
• ଆମେ ଏକ ବସ୍ତୁକୁ ଦେଖ୍ରୁ ଯଦି ଏହା ଆଲୋକ ନିର୍ଗତ କିମ୍ବା ପ୍ରତିଫଳିତ କରେ ।
• ଯେଉଁ ବସ୍ତୁଗୁଡ଼ିକ ନିଜସ୍ଵ ଆଲୋକ ପ୍ରଦାନ କରନ୍ତି । ସେଗୁଡ଼ିକୁ ଦୀପ୍ତ (Luminous) ବସ୍ତୁ କୁହାଯାଏ ।

→ ଉଦାହରଣ :

• ସୂର୍ଯ୍ୟ, ଜଳନ୍ତା ମହମବତୀ, କାଠ, କୋଇଲା ଓ ଗ୍ୟାସ୍ ଇତ୍ୟାଦି ।
• ଯେଉଁ ବସ୍ତୁଗୁଡ଼ିକ ନିଜର ଆଲୋକ ପ୍ରଦାନ କରନ୍ତି ନାହିଁ, ସେଗୁଡ଼ିକୁ ଦୀପ୍ତହୀନ (Non-Luminous) ବସ୍ତୁ କୁହାଯାଏ ।

→ ଉଦାହରଣ :

• ମାଟି, ପଥର, ଗଛ, ଟେବୁଲ, ଚୌକି ଇତ୍ୟାଦି ।
• ଦୀପ୍ତ ବସ୍ତୁରୁ ଅଦୀପ୍ତ ବସ୍ତୁ ଉପରେ ଆଲୋକ ପଡ଼ିଲେ ଆମେ ସେଗୁଡ଼ିକ ଦେଖୁଥାଉ ।
• ଅଦୀପ୍ତ ବସ୍ତୁଗୁଡ଼ିକ କିଛି ଆଲୋକ ଶୋକ କରି ଅବଶିଷ୍ଟ ଆଲୋକ ପ୍ରତିଫଳିତ କରି ଆମ ଆଖରେ ପଡ଼ିଲେ ସେଗୁଡ଼ିକ ଆମେ ଦେଖିଥାଉ ।

→ ଉଦାହରଣ :

• ଚନ୍ଦ୍ରର ନିଜର ଆଲୋକ ନାହିଁ । ତଥାପି ଆମେ ତାକୁ ରାତିରେ ଉଜ୍ଜ୍ବଳତା ପ୍ରଦର୍ଶନ କରୁଥିବାର ଦେଖୁ । ସୂର୍ଯ୍ୟାଲୋକ ଚନ୍ଦ୍ର ଉପରେ ପଡ଼ି ପ୍ରତିଫଳିତ ହୋଇ ପୃଥ‌ିବୀପୃଷ୍ଠରେ ଆମ ନିକଟରେ ପହଞ୍ଚ୍ ଥାଏ । ତେଣୁ ବାସ୍ତବରେ ଚନ୍ଦ୍ରାଲୋକ ହେଉଛି ପ୍ରତିଫଳିତ ସୂର୍ଯ୍ୟାଲୋକ ।
• କେତେକ ଦୀପ୍ତହୀନ ବସ୍ତୁକୁ ଦୀପ୍ତ କରାଯାଇପାରେ । ଅର୍ଥାତ୍ ସାଧାରଣ ତାପମାତ୍ରାରେ କୋଇଲା ଏକ ଦୀପ୍ତହୀନ ବସ୍ତୁ । ଏହାକୁ ଦହନ କଲେ ଏହା ଉଜ୍ଜ୍ବଳ ଆଲୋକ ପ୍ରଦାନ କରି ଦୀପ୍ତ ହୁଏ ।
• ଆଲୋକ ତାହାର ଉତ୍ସରୁ ସବୁ ଦିଗକୁ ସରଳରେଖାରେ ଗତିକରେ ।
• କାରଣ ଆଲୋକ ପଥରେ ଅସ୍ବଚ୍ଛ ବସ୍ତୁ ପାଇଲେ ସେହି ବସ୍ତୁର ଆକାର ଅନୁସାରେ ଛାୟା ସୃଷ୍ଟି ହୁଏ ।
• ଆଲୋକ ସହିତ ଅନେକ ପରିଘଟଣା ଜଡ଼ିତ ଯେପରିକି ଦର୍ପଣଦ୍ବାରା ପ୍ରତିବିମ୍ବ ଗଠନ, ତାରାମାନଙ୍କର ମିଞ୍ଜି ମିଞ୍ଜି ଆଲୋକ, ଇନ୍ଦ୍ରଧନୁର ସାତ ବର୍ଷ ଇତ୍ୟାଦି ।
• ଯେଉଁ ସରଳରେଖ୍ୟ ପଥରେ ଆଲୋକ ଗତି କରେ, ତାହାକୁ ଆଲୋକ ରଶ୍ମିଦ୍ଵାରା ସୂଚିତ କରାଯାଏ ।
• ଯଦି ଗୋଟିଏ ଅତି କ୍ଷୁଦ୍ର ଅସ୍ଵଚ୍ଛ ବସ୍ତୁ ଆଲୋକର ଗତିପଥରେ ରହିଯାଏ ତେବେ ସରଳରେଖାରେ ଗତିକରୁଥ‌ିବା ଆଲୋକ ସେହି ଅତି କ୍ଷୁଦ୍ର ବସ୍ତୁ ପାଖରେ ବାଙ୍କିଯାଏ, ଏହାକୁ ଆଲୋକର ବିକୀର୍ତ୍ତନ (Diffraction) କୁହାଯାଏ ।
• ଆଲୋକ କେବଳ ତରଙ୍ଗ ନୁହେଁ କି କେବଳ କଣିକା ନୁହେଁ । ଏହା ଉଭୟ ତରଙ୍ଗ ଓ କଣିକାର ଗୁଣ ପ୍ରଦର୍ଶନ କରେ । ଏହାକୁ ଆଲୋକର ଦ୍ଵୈତ ପ୍ରକୃତି (Dual nature of light) କୁହାଯାଏ ।

→ ଆଲୋକର ପ୍ରତିଫଳନ (Reflection of Light) :

• ଆଲୋକ ଚିକ୍କଣ ସମତଳ କିମ୍ବା ବକ୍ରପୃଷ୍ଠ ଉପରେ ପ୍ରତିଫଳିତ ହୋଇଥାଏ ।
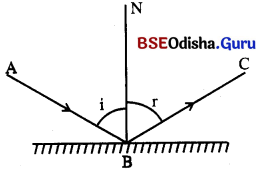
• ପ୍ରତିଫଳନରେ ଉଭୟ ଆପତିତ ରଶ୍ମି ଓ ପ୍ରତିଫଳିତ ରଶ୍ମି ଗୋଟିଏ ମାଧ୍ୟମରେ ରହିଥାଏ । ପ୍ରତିଫଳନର ଦୁଇଟି ନିୟମ ଅଛି
• ପ୍ରଥମ ନିୟମ : ଆଲୋକର ପ୍ରତିଫଳନ ବେଳେ ଆପତନ କୋଣ ଓ ପ୍ରତିଫଳନ କୋଣ ସମାନ ହୋଇଥାଏ ।
• ଦ୍ଵିତୀୟ ନିୟମ : ଆପତିତ ରଶ୍ମି, ପ୍ରତିଫଳିତ ରଶ୍ମି ଓ ଆପତନ ବିନ୍ଦୁରେ ପ୍ରତିଫଳନ ପୃଷ୍ଠ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ ଗୋଟିଏ ସମତଳରେ ରହିଥାନ୍ତି ।
• \(\bar{AB}\) – ଆପତିତ ରଶ୍ମି, \(\bar{BC}\) – ପ୍ରତିଫଳିତ ରଶ୍ମି, \(\bar{BN}\) – ଅଭିଲମ୍ବ
  

→ ସମତଳ ଦର୍ପଣଦ୍ୱାରା ଗଠିତ ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି :

• ପ୍ରତିଫଳନ ପୃଷ୍ଠ ସମତଳ ହେଲେ ତାହାକୁ ସମତଳ ଦର୍ପଣ କହନ୍ତି ।
• ସମତଳ ଦର୍ପଣ ଦ୍ବାରା ସୃଷ୍ଟି ହୋଇଥ‌ିବା ପ୍ରତିବିମ୍ବ ସର୍ବଦା ଆଭାସୀ ଓ ସଳଖ ହୋଇଥାଏ ।
• ଏହି ପ୍ରତିବିମ୍ବର ଆକାର ବସ୍ତୁର ଆକାର ସହିତ ସମାନ ହୋଇଥାଏ ।
• ସମତଳ ଦର୍ପଣ ସମ୍ମୁଖରେ ବସ୍ତୁ ଯେତିକି ଦୂରରେ ଥାଏ ତାହାର ପ୍ରତିବିମ୍ବ ଦର୍ପଣର ପଛପଟେ ସେତିକି ଦୂରରେ ରହିଥାଏ ।
  ଏହି ପ୍ରତିବିମ୍ବର ପାର୍ଶ୍ବ ଓଲଟା ହୋଇଥାଏ ।

→ ବର୍ତ୍ତୁଳ ଦର୍ପଣ (Spherical Mirror):
ଚକ୍ରପ୍ଷ୍ଠବିଶଷ୍ଟ ପ୍ରତିଫଳନକାର1 ତର୍ପଣକ୍ତ ବଫୁଲାକାର ତର୍ପଣ କହିନି | ତର୍ପଣର ପ୍ରତିଫଳନ ପୃଷ୍ଠ ଖୋଲକପୃଷ୍ଠର ଗୋଟିଏ ଅଂଶ ହୋଇଥାଏ । ବର୍ତ୍ତୁଳ ଦର୍ପଣ ଦୁଇ ପ୍ରକାରର; ଯଥା – ଅବତଳ ଦର୍ପଣ ଓ ଉତ୍ତଳ ଦର୍ପଣ ।

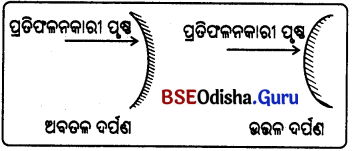
• ଅବତଳ ଦର୍ପଣ : ଯେଉଁ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପ୍ରତିଫଳନ ପୃଷ୍ଠ ଭିତର ଆଡ଼କୁ ବକ୍ର ହୋଇ ରହିଥାଏ, ତାହାକୁ ଅବତଳ (Concave) ଦର୍ପଣ କୁହାଯାଏ।
  • ଏହି ଦର୍ପଣର ବକ୍ର ପ୍ରତିଫଳନ ପୃଷ୍ଠ ଗୋଲକର କେନ୍ଦ୍ର ଆଡ଼କୁ ହୋଇଥାଏ ।
• ଉତ୍ତଳ ଦର୍ପଣ : ଯେଉଁ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପ୍ରତିଫଳନ ପୃଷ୍ଠ ବାହାର ଆଡ଼କୁ ବକ୍ର ହୋଇ ରହିଥାଏ ତାହାକୁ ଉତ୍ତଳ (Convex) ଦର୍ପଣ କୁହାଯାଏ ।
  • ଏହି ଦର୍ପଣର ବକ୍ର ପ୍ରତିଫଳନ ପୃଷ୍ଠ ଗୋଲକର କେନ୍ଦ୍ରର ବିପରୀତ ଦିଗରେ ରହିଥାଏ ।
  • କାଚ ଗୋଲକ ଖଣ୍ଡର ଭିତର (ଖାଲୁଆ) ପାଖରେ ରୁପାର ଲେପ ଦେଲେ ଉତ୍ତଳ ଦର୍ପଣ ମିଳେ ।
  • କାଚ ଗୋଲକ ଖଣ୍ଡର ବାହାର (ପେଟୁଆ) ପାଖରେ ରୁପାର ଲେପ ଦେଲେ ଅବତଳ ଦର୍ପଣ ମିଳିବ ।

→ (i) ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣ ସମ୍ପର୍କରେ ବ୍ୟବହୃତ ବୈଷୟିକ ଶବ୍ଦ (Term related to Spherical Mirror) :
ପୋଲ୍ (Pole) ବା ମେରୁ – ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ବକ୍ର ପ୍ରତିଫଳନ ପୃଷ୍ଠର କେନ୍ଦ୍ରକୁ ପୋଲ୍ (Pole) କହନ୍ତି । ଉଭୟ ଦର୍ପଣରେ ଏହାକୁ ସାଧାରଣତଃ P ଅକ୍ଷର ଦ୍ବାରା ଚିହ୍ନିତ କରାଯାଏ । ଏହା ଦର୍ପଣର ମଧ୍ୟବିନ୍ଦୁ ଅଟେ ଓ ଏହା ଦର୍ପଣର ପୃଷ୍ଠଦେଶରେ ଥାଏ ।

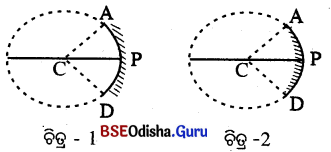
ଚିତ୍ର-1 ରେ APD ଗୋଟିଏ ଅବତଳ ଦର୍ପଣ ଏବଂ ଚିତ୍ର-2ରେ APD ଗୋଟିଏ ଉତ୍ତଳ ଦର୍ପଣ । ଉଭୟ ଦର୍ପଣର ମଝି ବିନ୍ଦୁ ସୂତାଦ୍ୱାରା ମାପି ପୋଲ୍ (P) ନିର୍ଣ୍ଣୟ କରାଯାଏ । ସେହି ବିନ୍ଦୁ P ଉତ୍ତଳ ବା ଅବତଳ ଦର୍ପଣର ମେରୁ ଅଟେ ।

→ (ii) ରକ୍ରତାକେତ୍ର (Centre of Curvature):
ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣ ଯେଉଁ ଫମ୍ପା ଗୋଲକର ଅଂଶ ହୋଇଥାଏ, ସେହି ଗୋଲକର ଜ୍ୟାମିତିକ କେନ୍ଦ୍ରକୁ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ବକ୍ରତା କେନ୍ଦ୍ର (Centre of Curvature) କୁହାଯାଏ । ଉଭୟ ଦର୍ପଣରେ ଏହାକୁ ସାଧାରଣତଃ (C) ଅକ୍ଷରଦ୍ଵାରା ଚିହ୍ନିତ କରାଯାଏ । ଏହା ପ୍ରତିଫଳନ ପୃଷ୍ଠର ବାହାରକୁ ରହିଥାଏ ।
‘ଅବତଳ ଦର୍ପଣ କ୍ଷେତ୍ରର ବଜ୍ରତା କେନ୍ଦ୍ର ଦର୍ପଣ ବାହାରେ ପ୍ରତିଫଳନ ପୃଷ୍ଠର ସମ୍ମୁଖରେ ଥାଏ । ଉତ୍ତଳ ଦର୍ପଣ କ୍ଷେତ୍ରରେ ବକ୍ରତା କେନ୍ଦ୍ର ଦର୍ପଣର ପ୍ରତିଫଳନ ପୃଷ୍ଠର ପଛଆଡ଼କୁ ରହିଥାଏ । ତେଣୁ ବକ୍ରତା କେନ୍ଦ୍ର ବର୍ତ୍ତୁଳ ଦର୍ପଣର ଅଂଶ ନୁହେଁ ।

→ (iii) ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ (Radius of Curvature) :
ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣ ଯେଉଁ ଗୋଲକର ଅଂଶ ହୋଇଥାଏ, ସେହି ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧକୁ ବର୍ତ୍ତୁଳାକର ଦର୍ପଣର ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ (Radius of Curvature) କୁହାଯାଏ । ଏହାକୁ ସାଧାରଣତଃ (R) ଅକ୍ଷର ଦ୍ଵାରା ଚିହ୍ନିତ କରାଯାଏ ।

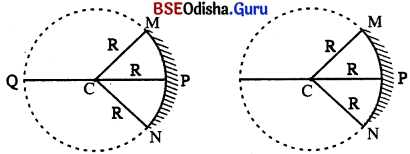
ପୋଲ୍ (P) ଓ ବକ୍ରତା କେନ୍ଦ୍ର C ମଧ୍ୟରେ ଥିବା ଦୂରତା PC ଦର୍ପଣର ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ ଅଟେ । ଏଠାରେ PC = CM = CN = R |

→ (iv) ପ୍ରମୁଖ ଅକ୍ଷ (Principal Axis) :
ଯେଉଁ ସରଳରେଖା ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପୋଲ୍ ଓ ବକ୍ରତା କେନ୍ଦ୍ରକୁ ଯୋଗ କରେ ତାହାକୁ ଦର୍ପଣର ପ୍ରମୁଖ ଅକ୍ଷ (Principal Axis )କୁହାଯାଏ । ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପ୍ରମୁଖ ଅକ୍ଷ ପୋଲ୍ ଉପରେ ଦର୍ପଣର ପୃଷ୍ଠପ୍ରତି ଅଭିଲୟ ହୋଇଥାଏ ।

→ ପ୍ରମୁଖ ଫୋକସ୍ (Principal Focus) :
ଅବତଳ ଦର୍ପଣର ଫୋକସ୍ : ମୁଖ୍ୟ ଅକ୍ଷସହିତ ସମାନ୍ତର ରହିଥ‌ିବା ଅନେକଗୁଡ଼ିଏ ଆଲୋକ ରଶ୍ମି ଅବତଳ ଦର୍ପଣରେ ପ୍ରତିଫଳିତ ହୋଇ ମୁଖ୍ୟ ଅକ୍ଷ ଉପରେ ଗୋଟିଏ ବିନ୍ଦୁରେ ମିଳିତ ହୁଅନ୍ତି ଏବଂ ପରସ୍ପରକୁ ଛେଦ କରନ୍ତି । ଏହି ବିନ୍ଦୁକୁ ଅବତଳ ଦର୍ପଣର ପ୍ରମୁଖ ଫୋକସ୍ (Principal Focus) କୁହାଯାଏ ।

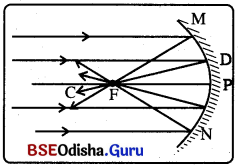
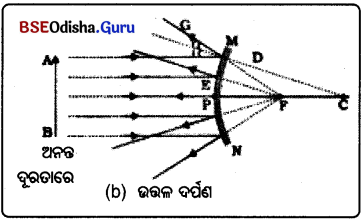
→ ଉତ୍ତଳ ଦର୍ପଣର ଫୋକସ୍ :
ମୁଖ୍ୟ ଅକ୍ଷସହ ସମାନ୍ତର ହୋଇ ଦର୍ପଣ ଉପରେ କେନ୍ଦ୍ରୀଭୂତ ନ ହୋଇ ପରସ୍ପରଠାରୁ ଦୂରେଇ ପାଇଚ୍ଛନ୍ତି | ଏହି ପ୍ରତିଫଳିତ ରଣ୍ଠିଖ୍ଡଡି.କ ପ୍ରମ୍ଭଗ ଅଷ ଯାଇଛନ୍ତି । ଏହି ପ୍ରତିଫଳିତ ରଶ୍ମିଗୁଡ଼ିକ ପ୍ରମୁଖ ଅକ୍ଷ ଉପରେ ଥ‌ିବା ଗୋଟିଏ ବିନ୍ଦୁରୁ ଆସିଲା ଭଳି ଜଣା ପଡ଼ୁଛି । ଏହି ବିନ୍ଦୁକୁ ଉତ୍ତଳ ଦର୍ପଣର ପ୍ରମୁଖ ଫୋକସ୍ କୁହାଯାଏ । ଫୋକସ୍ କୁହାଯାଏ ।

→ ଫୋକସ୍ ଦୂରତା (Focal Length) :
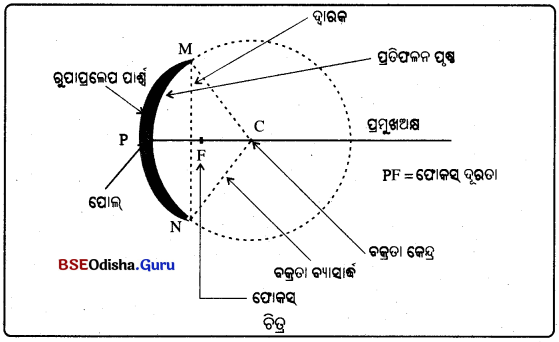
ବର୍ତ୍ତୁଳାକର ଦର୍ପଣର ପୋଲ୍ ଓ ଫୋକସ୍ ମଧ୍ୟରେ ଥିବା ଦୂରତାକୁ ଫୋକସ୍ ଦୂରତା (Focal length) କୁହାଯାଏ । ଏହାକୁ (f) ଅକ୍ଷର ଦ୍ବାରା ସୂଚିତ କରାଯାଏ । P ଓ F ମଧ୍ୟରେ ଥ‌ିବା ଦୂରତାକୁ ଫୋକସ ଦୂରତା (f) କହନ୍ତି ।

→ ତ୍ୱାରକ (Aperatures) :
ବର୍ତ୍ତୁଳାକର ଦର୍ପଣର ପ୍ରତିଫଳନ ପୃଷ୍ଠ ବର୍ତ୍ତୁଳାକାର ହୋଇଥାଏ । ଏହାର ଏକ ବୃତ୍ତାକାର ପରିସୀମା (Outline) ଥାଏ ।
ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପ୍ରତିଫଳନ ପୃଷ୍ଠର ବ୍ୟାସକୁ ଦର୍ପଣର ଦ୍ବାରକ କହନ୍ତି । MN ଦୂରତା ଦର୍ପଣର ଦ୍ଵାରକ ଅଟେ । ବର୍ତ୍ତୁଳ ଦର୍ପଣର ଦ୍ଵାରକ ବଜ୍ରତି ବ୍ୟାସାର୍ଷଠାରୁ ବହୁତ କମ୍ ।

→ ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ (R) ଓ ଫୋକସ୍ ଦୂରତା (f) ମଧ୍ୟରେ ସମ୍ପର୍କ :

• ଏକ କ୍ଷୁଦ୍ର ଦ୍ବାରକ ବିଶିଷ୍ଟ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣରେ ବକ୍ରତା ବ୍ୟାସାର୍କ ଏହାର ଫୋକସ୍ ଦୂରତାର ଦୁଇଗୁଣ ଅଟେ । ତେଣୁ R = 2f |
• ମୁଖ୍ୟ ଫୋକସ୍ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପୋଲ୍ ଓ ବକ୍ରତା କେନ୍ଦ୍ରର ଠିକ୍ ମଝିରେ ରହିଥାଏ ।

→ ଏ ବର୍ଭୁଳାକାର ଦର୍ପଣଦ୍ୱାରା ପ୍ରତିବିମ୍ବ ଗଠନ (Image Formation by Spherical Mirror) :

→ ରଶ୍ମିଚିତ୍ର ସାହାଯ୍ୟରେ ବର୍ତ୍ତୁଳ ଦର୍ପଣଦ୍ୱାରା ଗଠିତ ପ୍ରତିବିମ୍ବର ପରିପ୍ରକାଶ (Representation of Images formed by Spherical Mirrors using Ray Diagrams) :
ପ୍ରତିବିମ୍ବର ସ୍ଥିତି ଜାଣିବା ପାଇଁ ଯେକୌଣସି ଦୁଇଟି ରଶ୍ମିନେଇ ରଶ୍ମିଚିତ୍ର ଅଙ୍କନ କରାଯାଇ ପାରିବ । ଦୁଇଟି ପ୍ରତିଫଳିତ ରଶ୍ମିର ପ୍ରତିଚ୍ଛେଦ ବିନ୍ଦୁରେ ଏକ ବିନ୍ଦୁସମ ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟିହୁଏ ।
(i)

• ମୁଖ୍ୟ ଅକ୍ଷସହ ସମାନ୍ତର ଥ‌ିବା ଆଲୋକ ରଶ୍ମି ଅବତଳ ଦର୍ପଣ ଉପରେ ଆପତିତ ହେଲେ ପ୍ରତିଫଳିତ ରଶ୍ମି ଦର୍ପଣର ପ୍ରମୁଖ ଫୋକସ୍ ବିନ୍ଦୁଦେଇ ଗତିକରେ।
  
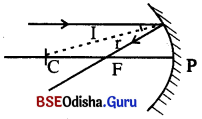
• ମୁଖ୍ୟ ଅକ୍ଷ ସହିତ ସମାନ୍ତର ଥ‌ିବା ଗୋଟିଏ ରଶ୍ମି ଉତ୍ତଳ ଦର୍ପଣ ଉପରେ ଆପତିତ ରଶ୍ମି ଉତ୍ତଳ ଏହ | ଉତ୍ତଳ ଦର୍ପଣ ଉପରେ ଆପତିତ ହେଲେ (divergent) ହେଲାଭଳି ଜଣାପଡ଼େ ।
  

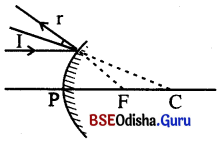
(ii)

• ଅବତଳ ଦର୍ପଣରେ ଗୋଟିଏ ରଶ୍ମି ଦର୍ପଣର ପ୍ରମୁଖ ଫୋକସ୍ ଦେଇ ଗତି କରି ଦର୍ପଣ ଉପରେ ଆପତିତ ହେଲେ, ତାହା ପ୍ରତିଫଳିତ ହୋଇ ଦର୍ପଣର ପ୍ରମୁଖ ଅକ୍ଷ ସହିତ ସମାନ୍ତର ହୋଇ ଗତି କରିବ । ଚିତ୍ର (a)
  
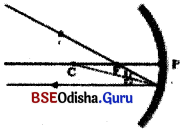
• ଉତ୍ତଳ ଦର୍ପଣରେ ଗୋଟିଏ ରଶ୍ମି ଦର୍ପଣର ପ୍ରମୁଖ ଫୋକସ୍ ଆଡ଼କୁ ଗତି କରୁଥିଲେ, ତାହା ଦର୍ପଣ ପୃଷ୍ଠରୁ ପ୍ରତିଫଳିତ ହେଲାପରେ ଦୁର୍ପଣର ପ୍ରମୁଖ ଅକ୍ଷ ସହ ସମାନ୍ତର ହୋଇ ଗତି କରେ । ଚିତ୍ର (b)
  

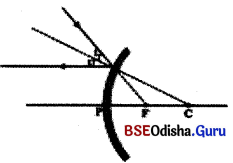
(iii)

• ଗୋଟିଏ ରଶ୍ମି ଅବତଳ ଦର୍ପଣର ବକ୍ରତା କେନ୍ଦ୍ର ଦେଇ ଗତିକରୁଥିଲେ କିମ୍ବା ଉତ୍ତଳ ଦର୍ପଣର ବକ୍ରତା କେନ୍ଦ୍ର ଆଡ଼କୁ ତା’ର ଦିଗ ନିର୍ଦ୍ଦେଶିତ ହୋଇଥିଲେ, ଦର୍ପଣ ପୃଷ୍ଠରୁ ପ୍ରତିଫଳନ ପରେ ତାହା ଯେଉଁ ପଥରେ ଆସିଥାଏ ସେହି ପଥରେ ଫେରିଯାଏ ।
  
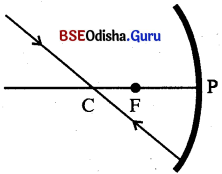
• ଆପତିତ ରଶ୍ମି ଦର୍ପଣର ପୃଷ୍ଠଉପରେ ପ୍ରତିଫଳନ ପୃଷ୍ଠର ଲମ୍ବ ଦିଗରେ ପଡ଼ିଲେ, ସେହି ରଶ୍ମି ଯେଉଁ ଦିଗରୁ ଆସିଥାଏ ସେହି ଦିଗରେ ଫେରିଯାଏ ।
  

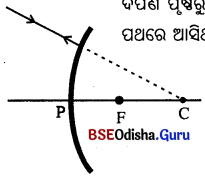
(iv) ଗୋଟିଏ ରଶ୍ମି ପ୍ରମୁଖ ଅକ୍ଷ ପ୍ରତି ତୀର୍ଯ୍ୟକ ଭାବରେ ଗୋଟିଏ ଅବତଳ ବା ଉତ୍କଳ ଦର୍ପଣ ପୃଷ୍ଠରେ ପୋଲ୍ (P) ବିନ୍ଦୁ ନିକଟରେ ଆପତିତ ହେଲେ, ତାହା ତୀର୍ଯ୍ୟକ ଭାବରେ ପ୍ରତିଫଳିତ ହୁଏ । ଆପତନ ବିନ୍ଦୁଠାରେ ଆପତିତ ରଶ୍ମି ଏପରି ଦିଗରେ ପ୍ରତିଫଳିତ ହୁଏ ଯେ ପ୍ରତିଫଳନ କୋଣ ଆପତନ କୋଣ ସହିତ ସମାନ ହୁଏ ।

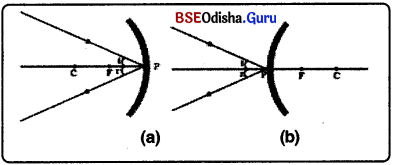
ଦର୍ପଣରେ ପ୍ରତିବିମ୍ବ ଗଠନ :

→ ଉତ୍ତଳ ଦର୍ପଣରେ ପ୍ରତିବିମ୍ବ ଗଠନ :

• ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣରେ ପ୍ରତିଫଳନ ପାଇଁ ପ୍ରଚଳିତ ସାଙ୍କେତିକ ପ୍ରଥା (Sign Convention for Reflection by Spherical Mirrors):
• ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣରେ ପ୍ରତିଫଳନ ସମ୍ପର୍କରେ ଆଲୋଚନା କଲାବେଳେ ସାଧାରଣ ଭାବେ ଯେଉଁ ଆଦୃତ ସଙ୍କେତ ପ୍ରଥା (Sign Convention) ସମୂହକୁ ଅନୁସରଣ କରାଯାଏ ତାହାକୁ ନୂତନ କାର୍ଟେସିଆନ ସଂକେତ ପ୍ରଥା (New cartesian sign convention) କୁହାଯାଏ ।
• ଏହି ପ୍ରଥାରେ ତର୍ପଣର ପୋଲକ୍ତ ମୂଳ ବିନ୍ଦୁ (Origin) ନିଆଯାଏ । ଦର୍ପଣର ପ୍ରମୁଖ ଅକ୍ଷକୁ ନିର୍ଦ୍ଦେଶୀ ପଦ୍ଧତି (Co-ordinate System)ର X-ଅକ୍ଷରୂପେ ନିଆଯାଏ ।

→ ଆଦୃତ ସଙ୍କେତ ଓ ପ୍ରଥାଗୁଡ଼ିକ ହେଲା—

• ବସ୍ତୁକୁ ସର୍ବଦା ଦର୍ପଣର ବାମ ପାର୍ଶ୍ଵରେ ରଖାଯାଏ ।
• ପ୍ରମୁଖ ଅକ୍ଷ ସହିତ ସମାନ୍ତର ରହିଥିବା ଦୂରତାଗୁଡ଼ିକୁ ଦର୍ପଣର ପୋଠାରୁ ମପାଯାଏ ।
• ଯେଉଁ ଦୂରତାକୁ ମୂଳ ବିନ୍ଦୁର ଡାହାଣ ଆଡ଼କୁ + X ଅକ୍ଷ ଦିଗରେ ମପାଯାଏ ତାହାକୁ ଯୁକ୍ତାତ୍ମକ ଓ ଯାହା ମୂଳବିନ୍ଦୁର ବାମ ଆଡ଼କୁ -X ଅକ୍ଷ ଦିଗରେ ମପାଯାଏ ତାହାକୁ ବିଯୁକ୍ତାତ୍ମକ ନିଆଯାଏ ।
• ପ୍ରମୁଖ ଅକ୍ଷର ଉପର ଆଡ଼କୁ +Y ଅକ୍ଷ ଦିଗରେ ଲମ୍ବ ଭାବରେ ଯେଉଁ ଦୂରତା ବା ଉଚ୍ଚତା ମପାଯାଏ ତାହାକୁ ଯୁକ୍ତାତ୍ମକ ନିଆଯାଏ ।
  
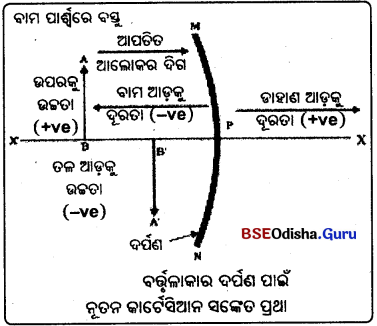
• ପ୍ରମୁଖ ଅକ୍ଷର ଚଳ ଆଡ଼କୁ –Y ଅକ୍ଷ ଦିଗରେ ଲମ୍ବଭାବରେ ଯେଉଁ ଦୂରତା ମପାଯାଏ ତାହାକୁ ବିଯୁକ୍ତାତ୍ମକ ନିଆଯାଏ ।

→ ଦର୍ପଣର ପୂତ୍ର (Mirror Formula) :

• ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପୋଠାରୁ ବସ୍ତୁର ଦୂରତାକୁ ବସ୍ତୁଦୂରତା (Object distance) ବା u, ଦର୍ପଣର ପୋଠାରୁ ପ୍ରତିବିମ୍ବର ଦୂରତାକୁ (Image distance) ପ୍ରତିବିମ୍ବ ଦୂରତା ବା v ଏବଂ ପୋଠାରୁ ଫୋକସ୍ ଦୂରତାକୁ f କୁହାଯାଏ ।
• ଏହି ତିନୋଟି ରାଶି u, v ଓ f ମଧ୍ୟରେ ଥ‌ିବା ସଂପର୍କ ହେଲା — \(\frac { 1 }{ u }\) + \(\frac { 1 }{ v }\) = \(\frac { 1 }{ f }\)
  
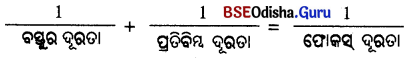
• ଏହି ସୂତ୍ର ସମସ୍ତ ଅବତଳ ଓ ଉତ୍କଳ ଦର୍ପଣ (ବର୍ତ୍ତୁଳ ଦର୍ପଣ) ପାଇଁ ପ୍ରଯୁଜ୍ୟ ।

→ ପରିବର୍ଦ୍ଧନ (Magnification) :

• ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣରେ ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହୋଇଥିଲା ବେଳେ ବସ୍ତୁର ଆକାର ତୁଳନାରେ ପ୍ରତିବିମ୍ବ କେତେ ପରିମାଣରେ ବର୍ଣିତ ହୋଇଛି, ତାହାକୁ
• ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣଦ୍ୱାରା ସୃଷ୍ଟି ହୋଇଥିବା ପରିବର୍ତ୍ତନ କୁହାଯାଏ ।
• ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା ଓ ବସ୍ତୁର ଉଚ୍ଚତାର ଅନୁପାତକୁ ଦର୍ପଣର ପରିବର୍ତ୍ତନ କହନ୍ତି ।
• m ଅକ୍ଷରକୁ ପରିବର୍ତ୍ତନ ସଙ୍କେତ ରୂପେ ନିଆଯାଏ ।
• ଯଦି ବସ୍ତୁର ଉଚ୍ଚତା h ଏବଂ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା h’ ହୁଏ
  
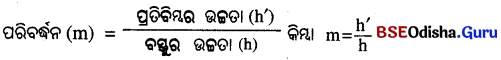
• ବସ୍ତୁର ଦୂରତା (u) ଓ ପ୍ରତିବିମ୍ବର ଦୂରତା (v) ସହିତ ପରିବର୍ତ୍ତନ (m) ର ସମ୍ପର୍କ ରହିଛି ତାହା ହେଲା
• 
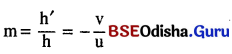
• ସାଧାରଣତଃ ବସ୍ତୁ, ପ୍ରମୁଖ ଅକ୍ଷର ଉପର ଆଡ଼କୁ ରହିଥାଏ, ତେଣୁ ବସ୍ତୁର ଉଚ୍ଚତା ଯୁକ୍ତାତ୍ମକ ନିଆଯାଏ । ଆଭାସୀ ପ୍ରତିବିମ୍ବ ପାଇଁ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତାକୁ
• ଯୁକ୍ତାତ୍ମକ ଓ ବାସ୍ତବ ପ୍ରତିବିମ୍ବ ପାଇଁ ତାହାର ଉଚ୍ଚତାକୁ ବିଯୁକ୍ତାତ୍ମକ ନିଆଯାଏ ।
• ପରିବର୍ଦ୍ଧନ (m) ସହିତ ବିଯୁକ୍ତ ଚିହ୍ନ ରହିଥିଲେ ପ୍ରତିବିମ୍ବ ବାସ୍ତବ ହୋଇଥାଏ ।
• ପରିବର୍ଦ୍ଧନ (m) ସହିତ ଯୁକ୍ତ ଚିହ୍ନ ରହିଥିଲେ ପ୍ରତିବିମ୍ବ ଆଭାସୀ ହୁଏ ।
• mର ମୂଲ୍ୟ ‘1’ ଠାରୁ କମ୍ ହେଲେ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା ବସ୍ତୁର ଉଚ୍ଚତା ତୁଳନାରେ କ୍ଷୁଦ୍ର ହୁଏ ।
• mର ମୂଲ୍ୟ ‘1’ ଠାରୁ ବଡ଼ ହେଲେ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା ବସ୍ତୁର ଉଚ୍ଚତା ତୁଳନାରେ ବଡ଼ ହୁଏ ।
• mର ମୂଲ୍ୟ ‘1’ ସହିତ ସମାନ ହେଲେ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା ବସ୍ତୁର ଉଚ୍ଚତା ତୁଳନାରେ ସମାନ ହୁଏ ।

→ ଆଲୋକର ପ୍ରତିସରଣ (Refraction of Light) :
ଆଲୋକର ପ୍ରତିସରଣ :

• ଆଲୋକ ତୀଯକ୍ ଭାବରେ ଗୋଟିଏ ସ୍ବଚ୍ଛ ମାଧ୍ୟମରୁ ଭିନ୍ନ ସାନ୍ଦ୍ରତା ବିଶିଷ୍ଟ ଅନ୍ୟ
• ଏକ ସ୍ୱଚ୍ଛ ମାଧ୍ୟମକୁ ଗତିକଲାବେଳେ ଦୁଇ ମାଧ୍ୟମର ସଂଯୋଗ ପୃଷ୍ଠରେ ଏହାର ଦିଗ ପରିବର୍ତ୍ତନକୁ ଆଲୋକର ପ୍ରତିସରଣ କହନ୍ତି

ତଦାହରଣ

• ଏକ କାଚପାତ୍ର ମଧ୍ୟରେ ଥ‌ିବା ଜଳଭିତରେ ବୁଡ଼ିରହିଥ‌ିବା ଏକ ଜିନଷକୁ ଦେଖ‌ିଲେ ସେଗୁଡ଼ିକ ବଡ଼ ଆକାରରେ ଦେଖାଦେବ ।
• ଏକ କାଚପାତ୍ର ମଧ୍ୟରେ ଥ‌ିବା ଜଳଭିତରେ ବୁଡ଼ିରହିଥିବା ଏକ ଜିନଷକୁ ଦେଖ‌ିଲେ ସେଗୁଡ଼ିକ ବଡ଼ ଆକାରରେ ଦେଖାଦେବ ।
• କାଚଗ୍ଲାସରେ ଥ‌ିବା ଜଳ ମଧ୍ୟରେ ବୁଡ଼ିରହିଥିବା ପେନ୍‌ସିଲ୍ ବଙ୍କା ଦେଖାଯିବ ।

→ କାରଣ :

• ଜଳସ୍ତରର୍ ଉପରେ ରହିଥ‌ିବା ବସ୍ତୁର ଅଂଶରୁ ଆଲୋକ ଆମ ପାଖକୁ ଯେଉଁ ଦିଗରୁ ଆସିଥାଏ, ତାହା ତୁଳନାରେ ଜଳ ମଧ୍ୟରେ ବୁଡ଼ି ରହିଥ୍‌ ବସ୍ତୁର ଅଂଶରୁ
• ଆଲୋକ ଆମ ଆଡ଼କୁ ଅନ୍ୟ ଦିଗରୁ ଆସିଲା ପରି ଜଣାପଡ଼େ । ଫଳରେ ଦୁଇଟି ପୃଷ୍ଠ ମଧ୍ୟରେ ବସ୍ତୁରୁ କିଛି ଅଂଶ ବିସ୍ଥାପିତ ହେଲାପରି ଜଣାଯାଏ ।

→ ପ୍ରତିସରଣର କାରଣ :

• ଯେତେବେଳେ ଆଲୋକ ରଶ୍ମି ଲଘୁ ମାଧ୍ୟମରୁ ଘନ ମାଧ୍ୟମକୁ ପ୍ରବେଶ କରେ, ଏହା ଅଭିଲମ୍ବଠାରେ ଥ‌ିବା ଅଭିଲମ୍ବ ଆଡ଼କୁ ବଙ୍କେଇ ଆସେ ।
• ଯେତେବେଳେ ଆଲୋକ ରଶ୍ମି ଘନ ମାଧ୍ୟମରୁ ଲଘୁ ମାଧ୍ୟମକୁ ପ୍ରବେଶ କରେ, ଏହା ଆପତନ ବିନ୍ଦୁଠାରେ ଥ‌ିବା ଅଭିଲମ୍ବଠାରୁ ଦୂରେଇ ଯାଏ ।
  • ପ୍ରଥମ ମାଧ୍ୟମରେ ଆଲୋକ ରଶ୍ମିକୁ ଆପତିତ ରଶ୍ମି କହନ୍ତି ।
  • ଦ୍ଵିତୀୟ ମାଧ୍ୟମରେ ଆଲୋକ ରଶ୍ମିକୁ ପ୍ରତିସୃତ ରଶ୍ମି କହନ୍ତି ।
  • ଆପତିତ ରଶ୍ମି ଅଭିଲମ୍ବ ସହ ଉତ୍ପନ୍ନ କରୁଥିବା କୋଣକୁ ଆପତନ କୋଣ (i) କହନ୍ତି ।
  • ପ୍ରତିସୃତ ରଶ୍ମି ଓ ଅଭିଲମ୍ବ ସହ ଉତ୍ପନ୍ନ କରୁଥିବା କୋଣକୁ ପ୍ରତିସରଣ କୋଣ (r) କହନ୍ତି ।

→ ପ୍ରତିସରଣର ଉଦାହରଣ (Examples of Refraction) :

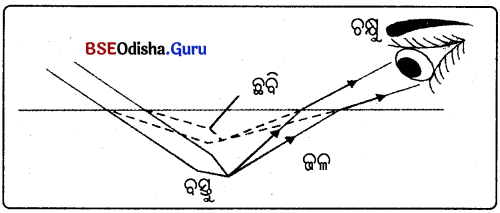
• ଜଳ ମଧ୍ୟରେ ପେନ୍‌ସିଲ୍‌କୁ ଆଂଶିକ ବୁଡ଼ାଇ ଦିଆଯାଇଛି ।
• A ଠାରୁ ନିର୍ଗତ ହେଉଥ‌ିବା ଆଲୋକ ରଶ୍ମି ଜଳ ଓ ବାୟୁର ବ୍ୟବଧାନ ପୃଷ୍ଠଠାରେ ବଙ୍କେଇ ଯାଇଛି ।
• ରଶ୍ମିଟି ଆଜ୍‌ରେ ପଡ଼ିଲେ ତାହା A’ରୁ ଆସିଲାଭଳି ଜଣାଯାଉଛି ।
• A ବିନ୍ଦୁଟି A’ ଠାରେ ଥଲାଭଳି ଜଣାଯାଉଛି । OA, OA’ ଭଳି ଜଣାପଡ଼େ ।
• ଜଳସ୍ତରର ଉପରେ ରହିଥ‌ିବା ପେନ୍‌ସିଲ୍‌ର ଅଂଶରୁ ଆଲୋକ ଆଖୁକୁ ଯେଉଁ ଦିଗରୁ ଆସୁଛି ତାହା ତୁଳନାରେ ଜଳ ମଧ୍ୟରେ ବୁଡ଼ି ରହିଥ୍ୟା ପେନ୍‌ସିଲ୍‌ର ଅଂଶରୁ ଆଲୋକ ଆଖୁ ଆଡ଼କୁ ଅନ୍ୟ ଦିଗରୁ ଆସିଲା ଭଳି ଜଣାପଡ଼ୁଛି । ତେଣୁ ପେନ୍‌ସିଲ୍‌ ବଙ୍କା ଦେଖାଯାଉଛି ।

→ ଆୟତାକାର କାଚସ୍ଲାବ୍ ମଧ୍ୟରେ ପ୍ରତିସରଣ (Refraction through a Rectangular Glass Slab) :

→ ବର୍ତ୍ତୁଳାକାର ଲେନ୍ସରେ ପ୍ରତିସରଣ (Refraction by Spherical Lenses) :

ଲେନ୍ସ :

• ଦୁଇଟି ପୃଷ୍ଠ ଥ‌ିବା ଏକ ସ୍ଵଚ୍ଛ ପ୍ରତିସରଣକାରୀ ମାଧ୍ୟମରେ ଗୋଟିଏ ପୃଷ୍ଠ ବା ଉଭୟ ପୃଷ୍ଠ ବିକ୍ର ହୋଇଥିଲେ ତାହାକୁ ଲେନସ୍ କୁହାଯାଏ ।
  
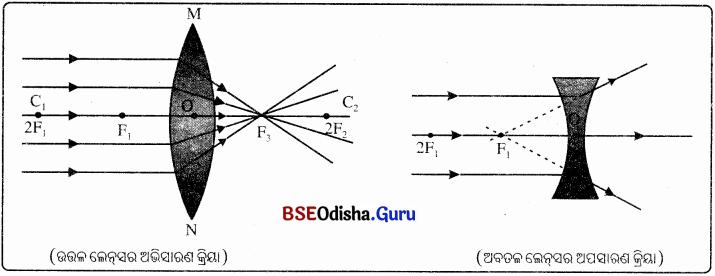
• ଲେନସ୍ ଦୁଇ ପ୍ରକାରର— (a) ଉତ୍ତଳ ଲେନସ୍ ଓ (b) ଅବତଳ ଲେନସ୍ ।

(a) ଉତ୍ତଳ ଲେନସ୍‌ :

• ଯେଉଁ ଲେନସ୍‌ର ଦୁଇଟି ବର୍ତ୍ତୁଳାକାର ପୃଷ୍ଠ ବାହାର ପଟକୁ ବାହାରିଥାଏ, ସେହି ଲେନ୍‌ସ୍‌କୁ ଦ୍ୱି-ଉତ୍ତଳ ବା କେବଳ ଉତ୍ତଳ ଲେନ୍ସ କୁହାଯାଏ ।
• ଉତ୍ତଳ ଲେନ୍ସର ମଝି ଅଂଶ ମୋଟା ଓ ଧାର ଆଡ଼କୁ କ୍ରମଶଃ ପତଳା ।
• ଉତ୍ତଳ ଲେନସ୍ ଆଲୋକ ରଶ୍ମିଗୁଚ୍ଛକୁ କେନ୍ଦ୍ରାଭିମୁଖୀ (Converge) କରେ । ତେଣୁ ଉତ୍ତଳ ଲେନସ୍‌ କେନ୍ଦ୍ରାଭିମୁଖୀ ବା ଅଭିସାରୀ ଲେନସ୍ କୁହାଯାଏ ।

(b) ଅବତଳ ଲେନସ୍ :

• ଯେଉଁ ଗୋଟିଏ ଲେନ୍ସର ଦୁଇଟି ବର୍ତ୍ତୁଳାକାର ପୃଷ୍ଠ ଯଦି ଭିତର ଆଡ଼କୁ ପଶିଯାଇଥାଏ ଅର୍ଥାତ ବକ୍ରହୋଇଥାଏ ତେବେ ତାହାକୁ ଦ୍ୱି-ଅବତଳ ବା କେବଳ ଅବତଳ ଲେନସ୍ କହନ୍ତି ।
• ଏହାର ଧାର ଅଂଶ ମଝି ଅଂଶ ଅପେକ୍ଷା ଅଧିକ ମୋଟା ହୋଇଥାଏ ।
• ଏହି ଲେନସ୍ ଆଲୋକ ରଶ୍ମି ଅପସାରଣ (Diverge) କରେ । ତେଣୁ ଅବତଳ ଲେନ୍ସକୁ ଅପସାରୀ ଲେନ୍ସ କୁହାଯାଏ ।

→ ଲେନ୍ସର ବିଭିନ୍ନ ଅଂଶ :
ବକ୍ରତା କେନ୍ଦ୍ର :

• ଗୋଟିଏ ଉତ୍ତଳ କିମ୍ବା ଅବତଳ ଲେନ୍ସର ଦୁଇଟି ବର୍ତ୍ତୁଳାକାର ପୃଷ୍ଠ ଥାଏ । ଲେସର ପ୍ରତ୍ୟେକ ବର୍ତ୍ତୁଳାକାର ପୃଷ୍ଠ ଗୋଟିଏ ଗୋଲକର ଅଂଶ ଅଟେ ।
• ଏହି ଗୋଲକଗୁଡ଼ିକର କେନ୍ଦ୍ରକୁ ଲେନ୍‌ସର ବକ୍ରତା କେନ୍ଦ୍ର (Centre of Curvature) କୁହାଯାଏ । ଲେନ୍ସର ବଜ୍ରତା କେନ୍ଦ୍ର ସାଧାରଣତଃ ‘C’ ଅକ୍ଷରଦ୍ଵାରା ଚିହ୍ନିତ ହୋଇଥାଏ ।

ଲେନସ୍‌ର ଦୁଇଟି ବକ୍ରତଳ ପାଇଁ ଦୁଇଟି ବକ୍ରତା କେନ୍ଦ୍ର ଥାଏ । ତାହାକୁ C₁ ଓ C₂ ଅକ୍ଷର ଦ୍ଵାରା ଚିହ୍ନିତ କରାଯାଏ ।

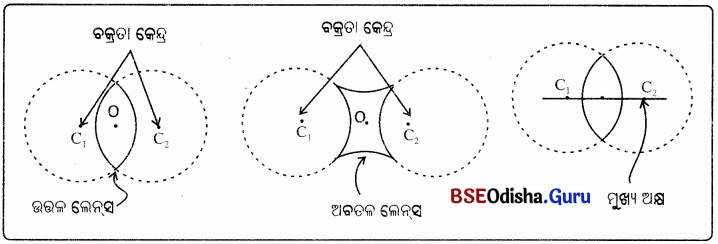
→ ପ୍ରମୁଖ ଅକ୍ଷ (Principal Axis) :
ଲେନ୍‌ସର ଦୁଇ ବକ୍ରତା କେନ୍ଦ୍ର ଦେଇ ଯାଇଥବା କାଳ୍ପନିକ ସରଳରେଖାକୁ ଲେନ୍ସର ପ୍ରମୁଖ ଅକ୍ଷ କୁହାଯାଏ ।

→ ଆଲୋକ କେନ୍ଦ୍ର (Optical Centre) :
ଲେନ୍ସର ମଧ୍ୟବିନ୍ଦୁକୁ ଆଲୋକ କେନ୍ଦ୍ର କୁହାଯାଏ । ଲେନ୍ସର ଆଲୋକ କେନ୍ଦ୍ରଦେଇ ଯାଉଥିବା ଆଲୋକ ରଶ୍ମିର କୌଣସି ବିପଥନ (Deviation) ହୁଏନାହିଁ ଓ ତାହା ସିଧା ଗତିକରେ । ଏହାକୁ ‘O’ ଅକ୍ଷରଦ୍ବାରା ଚିହ୍ନିତ କରାଯାଏ ।

→ ଦ୍ଵାରକ (Aperture) :
ବର୍ତ୍ତୁଳାକାର ଲେନ୍ସର ମଝିରେ ଯେଉଁ କ୍ଷୁଦ୍ର ବୃତ୍ତାକାର ପରିସୀମା (Outline) ଭିତରେ ଲେନ୍ସ ପ୍ରତିସରଣ କରେ ତାହାର ବ୍ୟାସକୁ ଲେନ୍ସର ଦ୍ଵାରକ କହନ୍ତି ।
ଲେନ୍‌ସର ଦ୍ଵାରକ, ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ ଅପେକ୍ଷା ଯଥେଷ୍ଟ କମ୍ । ଏହି ଲେନସ୍‌ଗୁଡ଼ିକୁ କ୍ଷୁଦ୍ର ଦ୍ବାରକ ବିଶିଷ୍ଟ ପତଳା ଲେନ୍ସ (Thin Lense) କୁହାଯାଏ ।

→ ଲେନ୍ସଗୁଡ଼ିକଦ୍ଵାରା ପ୍ରତିବିମ୍ବ ଗଠନ (Image formation by Lenses):

→ ରଶ୍ମି ଚିତ୍ର ବ୍ୟବହାର କରି ଲେନ୍ସରେ ପ୍ରତିବିମ୍ବ ଗଠନ (Image Formation by Lenses Using Ray Diagrams):
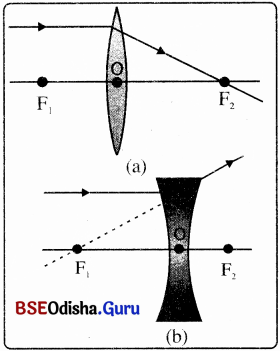
(i)

• ପ୍ରମୁଖ ଅକ୍ଷ ସହିତ ସମାନ୍ତର ହୋଇ ବସ୍ତୁରୁ ଆସୁଥ‌ିବା ଆଲୋକ ରଶ୍ମି ଉତ୍ତଳ ଲେନ୍ସରେ ପ୍ରତିସୃତ ହେଲା ପରେ, ଲେନ୍ସର ଅପର ପାର୍ଶ୍ଵରେ ପ୍ରମୁଖ ଫୋକସ୍ ଦେଇ ଗତି କରେ । ଚିତ୍ର (a)
• ଅବତଳ ଲେନ୍ସ କ୍ଷେତ୍ରରେ ସେହି ରଶ୍ମି ଲେନ୍ସର ବସ୍ତୁ ରହିଥ‌ିବା ପାର୍ଶ୍ବରେ ଥ‌ିବା ଫୋକସ୍‌ ଅପସାରିତ ହେଲାପରି ଜଣାପଡ଼େ । ଚିତ୍ର (b)
  

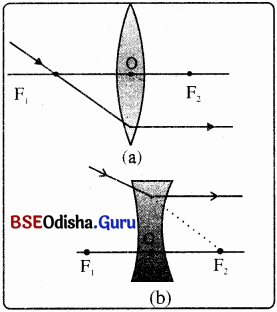
(ii)

• ପ୍ରମୁଖ ଫୋକସ୍ ଦେଇ ଗତି କରୁଥିବା ଗୋଟିଏ ଆଲୋକ ରଶ୍ମିର ଉତ୍ତଳ ଲେନ୍ସରେ ପ୍ରତିସରଣ ହେଲା ପରେ, ତାହା ପ୍ରମୁଖ ଅକ୍ଷ ସହିତ ସମାନ୍ତର ହୋଇ ଲେନ୍ସରୁ ନିର୍ଗତ ହୁଏ । ଚିତ୍ର (a)
• ଯେଉଁ ଆଲୋକ ରଶ୍ମି ଅବତଳ ଲେନ୍ସର ଫୋକସ୍ ଆଡ଼କୁ ଗତି କରୁଥାଏ ତାହା ସେହି ଲେନ୍ସ ଦ୍ଵାରା ପ୍ରତିସୃତ ହେଲା ପରେ, ପ୍ରମୁଖ ଅକ୍ଷ ସହିତ ସମାନ୍ତର ଭାବେ ଲେନ୍ସରୁ ନିର୍ଗତ ହୁଏ । ଚିତ୍ର (b)
  

(iii) ଉଭୟ ଉତ୍ତଳ ଓ ଅବତଳ ଲେନ୍ସର ଆଲୋକ କେନ୍ଦ୍ର ଦେଇ ଗତି କରୁଥିବା ଆଲୋକ ରଶ୍ମି, କୌଣସି ବିପଥନ (Deviation )ବିନା ଲେନ୍ସରୁ ନିର୍ଗତ ହୁଏ ।

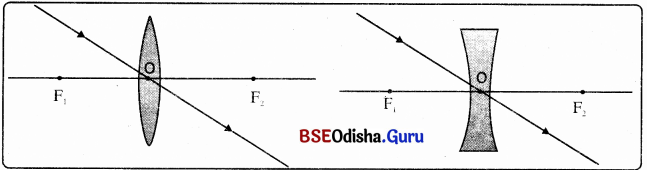
କେତେକ ଭିନ୍ନ ଭିନ୍ନ ସ୍ଥିତି ପାଇଁ ଉତ୍ତଳ ଲେନ୍ସରେ ପ୍ରତିବିମ୍ବ ଗଠନର ରଶ୍ମିଚିତ୍ର :

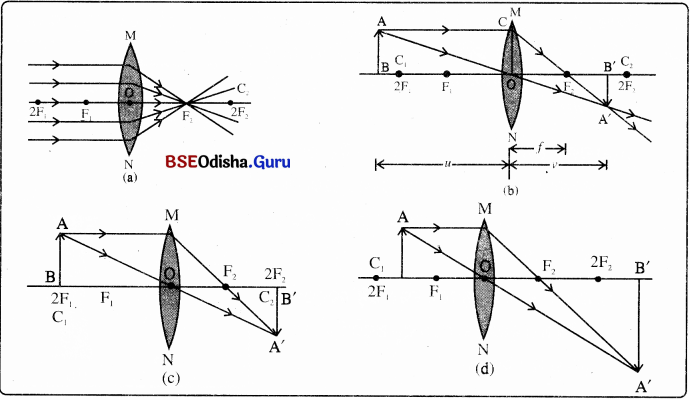
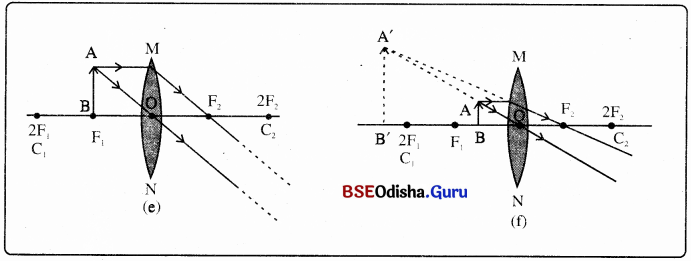
କେତେକ ଭିନ୍ନ ଭିନ୍ନ ସ୍ଥିତି ପାଇଁ ଅବତଳ ଲେନ୍ସରେ ପ୍ରତିବିମ୍ବ ଗଠନର ରଶ୍ମିଚିତ୍ର

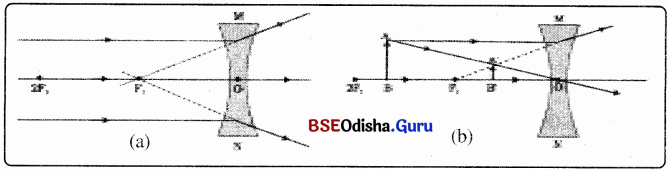
→ ବତ୍ତୁଲାକାର ଲେନସ ପାଇଁ ସଙ୍କେତ ପ୍ରଥା (Sign Convention for Spherical Lenses) :

• ସମସ୍ତ ଦୂରତା ଲେନସ୍‌ର ଆଲୋକ କେନ୍ଦ୍ରଠାରୁ ମପାଯାଏ ।
• ଉତ୍ତଳ ଲେନସ୍‌ର ଫୋକସ୍ ଦୂରତା ଯୁକ୍ତାତ୍ମକ ।
• ଅବତଳ ଲେନସ୍‌ର ଫୋକସ୍ ଦୂରତା ବିଯୁକ୍ତାତ୍ମକ ।
• ଆଲୋକକେନ୍ଦ୍ରଠାରୁ ବସ୍ତୁର ଦୂରତା, ପ୍ରତିବିମ୍ବର ଦୂରତା ଓ ଫୋକସର ଦୂରତାକୁ ଯଥାକ୍ରମେ u, v ଓ f ଲେଖାଯାଏ, ବସ୍ତୁର ଉଚ୍ଚତା (h) ଏବଂ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା (h’) ରୂପେ ନିଆଯାଏ ।
  
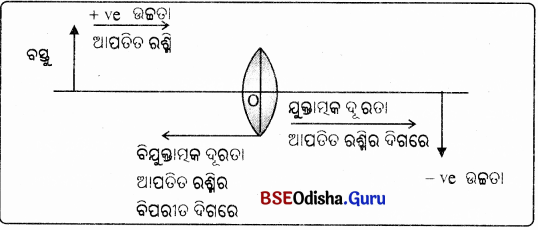
• ବାସ୍ତବ ପ୍ରତିବିମ୍ବର ଦୂରତା ଯୁକ୍ତାତ୍ମକ ଓ ଆଭାସୀ ପ୍ରତିବିମ୍ବର ଦୂରତା ବିଯୁକ୍ତାତ୍ମକ ।
• ବସ୍ତୁର ଉଚ୍ଚତା ସର୍ବଦା ଯୁକ୍ତାତ୍ମକ, ଆଭାସୀ ଓ ସଳଖ, ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା ଯୁକ୍ତାତ୍ମକ, ବାସ୍ତବ ଓ ଓଲଟା ତେଣୁ

→ ଲେନସର ସୂତ୍ର ଓ ପରିବର୍ଦ୍ଧନ (Lens Formula and Magnification) :
ଉଭୟ ଉତ୍ତଳ ଓ ଅବତଳ ଲେନ୍‌ସ୍‌ ପାଇଁ ବସ୍ତୁର ଦୂରତା (u), ପ୍ରତିବିମ୍ବ ଦୂରତା (v) ଓ ଫୋକସ୍ ଦୂରତା (f) ହେଲେ,

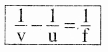
ଏହି ଲେନସ୍ ସୂତ୍ର ଯେକୌଣସି ବର୍ତ୍ତୁଳାକାର ଲେନସ୍ ପାଇଁ ପ୍ରଯୁଜ୍ୟ ।

→ ପରିବର୍ତ୍ତନ (Magnification) :
ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା ଓ ବସ୍ତୁର ଉଚ୍ଚତାର ଅନୁପାତକୁ ଲେନସଦ୍ୱାରା ସୃଷ୍ଟ ପରିବର୍ତନ କୁହାଯାଏ । ପରିବର୍ତ୍ତନକୁ m ଅକ୍ଷରଦ୍ୱାରା ଚିହ୍ନିତ କରାଯାଏ । ଯଦି ବସ୍ତୁର ଉଚ୍ଚତା h ହୁଏ ଓ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା h’ ହୁଏ ତେବେ

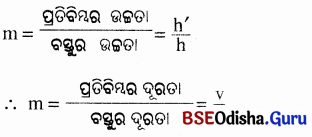
ପରିବର୍ଦ୍ଧନ = \(\frac { h’ }{ h }\) = \(\frac { v }{ u }\)

→ ଲେନ୍ସର ପାୱାର (Power of a Lens) :
ଲେନ୍‌ସଦ୍ବାରା ହେଉଥ‌ିବା ଅଭିସାରଣ ବା ଅପସାରଣର ମାତ୍ରାକୁ ଲେନସ୍‌ର ପାୱାର କୁହାଯାଏ । ଗୋଟିଏ ଲେନ୍ସର ଫୋକସ୍ ଦୂରତାର ବିଲୋମୀ (Reciprocal)କୁ ଲେନ୍ସର ପାୱାର କୁହାଯାଏ । ଏହାକୁ P ଅକ୍ଷରରେ ଚିହ୍ନିତ କରାଯାଏ । ଯଦି ଲେନ୍‌ସର ଫୋକସ୍ ଦୂରତା f ହୁଏ ତେବେ
P = \(\frac { 1 }{ f }\)

• ଆନ୍ତର୍ଜାତିକ ଏକକ ପଦ୍ଧତି (SI unit) ଅନୁସାରେ ଲେନସ୍‌ର ପାୱାରର ଏକକ ଡାୟପ୍‌ଟର (Diopter) | ଏହାକୁ D ଅକ୍ଷର ଦ୍ଵାରା ଚିହ୍ନିତ କରାଯାଏ।
• ଫୋକସ୍ ଦୂରତା ମିଟରରେ ପ୍ରକାଶିତ ହେଲେ ପାଓ୍ବାର ଡାୟପ୍‌ଟରରେ ପ୍ରକାଶିତ ହୁଏ ।
• ଲେନସ୍‌ର ଫୋକସ ଦୁରତା 1.0) ମି ହେଲେ ତା’ର ପାୱାର । ଡାୟପ୍‌ଟର ହୋଇଥାଏ ।
  1D = 1 ମି^-1 ବା 1 m^-1
• ଉତ୍ତଳ ଲେନ୍ସର ପାୱାରକୁ ଯୁକ୍ତାତ୍ମକ ଓ ଅବତଳ ଲେନସ୍‌ର ପାୱାରକୁ ବିଯୁକ୍ତାତ୍ମକ ମନେ କରାଯାଇଛି ।