BSE Odisha 9th Class Maths Solutions Algebra Chapter 2 ବାସ୍ତବ ସଂଖ୍ୟା Ex 2(b)

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 2 ବାସ୍ତବ ସଂଖ୍ୟା Ex 2(b) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 2 ବାସ୍ତବ ସଂଖ୍ୟା Ex 2(b)

Question 1.
ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନମାନଙ୍କରେ ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛ ।

(i) ନିମ୍ନଲିଖୂତ ମଧ୍ୟରୁ କେଉଁଟି ଠିକ୍ ?
(a) √4 ଏକ ଅପରିମେୟ ସଂଖ୍ୟା
(b) √2 ଓ √3 ମଧ୍ୟରେ ଅପରିମେୟ ସଂଖ୍ୟା ନାହିଁ
(c) √8 ଏକ ଅପରିମେୟ ସଂଖ୍ୟା
(d) π ∈ Q
ସମାଧାନ:
√8 ଏକ ଅପରିମେୟ ସଂଖ୍ୟା
√8 = 2√2 ଏକ ଅପରିମେୟ ସଂଖ୍ୟା ଉତ୍ତରଟି ଠିକ୍ ।

(ii) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଠିକ୍ ନୁହେଁ ?
(a) p ଓ q ସଂଖ୍ୟାଦ୍ଵୟ ଯଥାକ୍ରମେ ପରିମେୟ ଓ ଅପରିମେୟ ହେଲେ p + q ଅପରିମେୟ
(b) p ଓ q ସଂଖ୍ୟାଦ୍ଵୟ ଅପରିମେୟ ହେଲେ p + q ଅପରିମେୟ
(c) p ଓ q ସଂଖ୍ୟାଦ୍ଵୟ ପରିମେୟ ହେଲେ p + q ପରିମେୟ
(d) p ଓ q ସଂଖ୍ୟାଦ୍ଵୟ ପରିମେୟ ହେଲେ p – q ପରିମେୟ
ସମାଧାନ:
p ଓ q ସଂଖ୍ୟାଦ୍ଵୟ ଯଥାକ୍ରମେ ପରିମେୟ ଓ ଅପରିମେୟ ହେଲେ p + q ଅପରିମେୟ
ଅପରିମେୟ ସଂଖ୍ୟାରେ ଯୋଗ ସଂବୃତ୍ତି ନିୟମ ପାଳନ କରେ ନାହିଁ ।

(iii) ନିମ୍ନଲିଖୂତ ମଧ୍ୟରୁ କେଉଁଟି ଠିକ୍ ?
(a) p ଓ q ପରିମେୟ ହେଲେ pq ପରିମେୟ
(b) p ଓ q ଅପରିମେୟ ହେଲେ pq ଅପରିମେୟ
(c) p ପରିମେୟ ଓ ରୁ ଅପରିମେୟ ହେଲେ pq ପରିମେୟ
(d) p ଓ q ଅପରିମେୟ ହେଲେ p/q ଅପରିମେୟ
ସମାଧାନ:
p ଓ q ପରିମେୟ ହେଲେ pq ପରିମେୟ
ପରିମେୟ ସଂଖ୍ୟାରେ ଗୁଣନ ପ୍ରକ୍ରିୟା ସବୃତ୍ତି ନିୟମ ପାଳନ କରେ ।

(iv) ରାଡ଼ିକାଲ (କରଣୀ) ଚିହ୍ନ ବ୍ୟବହାର କଲେ 2? ରାଶିଟି କାହା ସହ ସମାନ ?
(a) √2
(b) \(\sqrt[3]{2}\)
(c) √8
(d) ଏଥରୁ କେଉଁଟି ନୁହେଁ
ସମାଧାନ:
√2
\(2^{\frac{1}{2}}\) = √2

(v) ଡ଼ିକାଲ ଚିହ୍ନ ଅପସାରଣ କଲେ -3 ରାଶିର ସରଳୀକୃତ ମାନ କେଉଁଟି ?
(a) \(\frac{x^{\frac{3}{5}}}{2}\)
(b) \(\frac{1}{2 x^{-15}}\)
(c) \(\frac{x^{15}}{2}\)
(d) ଏଥରୁ କେଉଁଟି ନୁହେଁ
ସମାଧାନ:
\(\frac{x^{\frac{3}{5}}}{2}\)
\(\frac{1}{2 \sqrt[5]{x^{-3}}}=\frac{1}{2 x^{-\frac{3}{3}}}=\frac{x^{\frac{3}{5}}}{2}\)

(vi) \(9^{-1 \frac{1}{2}}\) ରାଶିଟି କେଉଁ ରାଶି ସହ ସମାନ ?
(a) \(\frac{1}{3}\)
(b) \(3 \frac{1}{3}\)
(c) \(\frac{1}{9}\)
(d) \(\frac{1}{27}\)
ସମାଧାନ:
\(\frac{1}{27}\)
\(9^{-\frac{1}{2}}=\left(3^2\right)^{\frac{-3}{2}}=3^{-3}=\frac{1}{3^3}=\frac{1}{27}\)

(vii) \(\left(\sqrt{2}^{\sqrt{2}^{\sqrt{2}}}\right)\) ର ମୁଲ୍ୟ ଲାହା ସହ ସମାନ ?
(a) √2
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{\sqrt{2}}\)
(d) 2
ସମାଧାନ:
2
\(\sqrt{2}^{\sqrt{2}^{\sqrt{2}}}=\sqrt{2}^{\left(2^{\frac{1}{2}}\right)^{\frac{1}{2}}}=\sqrt{2}^{2^{\frac{1}{2}+\frac{1}{2}}}=(\sqrt{2})^2\) = 2

(viii) କେଉଁବି ଠିଳ୍?
(a) \(\sqrt[4]{4}>\sqrt[3]{3}\)
(b) \(\sqrt[3]{4}>\sqrt[4]{3}\)
(c) \(\sqrt[3]{4}=\sqrt[4]{3}\)
(d) \(\sqrt[4]{4}=\sqrt[3]{3}\)
ସମାଧାନ:
\(\sqrt[3]{4}>\sqrt[4]{3}\)
\((\sqrt[3]{4})^{12}=4^{\frac{12}{3}}=4^4=256,(\sqrt[4]{3})^{12}=3^{\frac{12}{4}}=3^3\) = 27

(ix) Q ସମସ୍ତ ପରିମେୟ ସଂଖ୍ୟା ଓ ତୁ ସମସ୍ତ ଅପରିମେୟ ସଂଖ୍ୟା ହେଲେ Q – Q’ = ?
(a) N
(b) Z
(c) R
(d) ଏଥୁରୁ କେଉଁଟି ନୁହେଁ
ସମାଧାନ:
R
Q ସମସ୍ତ ପରିମେୟ ସଂଖ୍ୟା, Q’ ସମସ୍ତ ଅପରିମେୟ ସଂଖ୍ୟା ହେଲେ Q ∪ Q’ = R

(x) ନିମ୍ନଲିଖୂତ ମଧ୍ୟରୁ x ର ମୂଲ୍ୟ କେଉଁଟି ହେଲେ (√5 + √2) x ଏକ ପରିମେୟ ସଂଖ୍ୟା ହେବ ?
(a) √5 + √2
(b) √5 – √2
(c) √5
(d) √2
ସମାଧାନ:
√5 – √2
(√5 + √2) x ଏକ ପରିମେୟ ସଂଖ୍ୟା ହେଲେ x = √5 – √2
ଲାରଣ : (√5 + √2) (√5 – √2) = √5 – √2 = 3

(xi) x + (1 – √2 ) ଏକ ପରିମେୟ ସଂଖ୍ୟା ହେଉଥ୍ଲେ ନିମ୍ନଲିଖିତ ମୂଲ୍ୟରୁ xର ମୂଲ୍ୟଟି ବାଛ ।
(a) 1 – √2
(b) √2 – 1
(c) -1 – √2
(d) 2√2
ସମାଧାନ:
√2 – 1
x + (1 – √2) ଏକ ପରିମେୟ ସଂଖ୍ୟା ହେଲେ, x = √2 – 1
ଲାରଣ : √2 – 1 + 1 – √2 = 0 ∈ Q

(xii) \(\frac{\sqrt{2}}{\sqrt{3}}\) ସଂଖ୍ୟାଟି ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ସହ ସମାନ ନୁହେଁ ?
(a) \(\frac{4}{\sqrt{6}}\)
(b) \(\frac{\sqrt{6}}{3}\)
(c) \(\frac{2}{\sqrt{6}}\)
(d) \(\frac{\sqrt{12}}{\sqrt{18}}\)
ସମାଧାନ:
\(\frac{4}{\sqrt{6}}\)
\(\frac{\sqrt{2}}{\sqrt{3}} \neq \frac{4}{\sqrt{6}}\), (ଲାରଣ : \(\frac{\sqrt{2}}{\sqrt{3}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{2}{\sqrt{6}}\))

(xiii) 3√2 ଓ 7√8 ର ଯୋଗଫଳ କେତେ ?
(a) 12√2
(b) 10√2
(c) 10√8
(d) ଏଥୁରୁ କେଉଁଟି ନୁହେଁ
ସମାଧାନ:
ଏଥୁରୁ କେଉଁଟି ନୁହେଁ
3√2 + 7√8 = 3√2 + 14√2 = 17√2

Question 2.
ନିମ୍ନୋକ୍ତ ଉକ୍ତି ମଧ୍ୟରୁ ଯେଉଁଗୁଡ଼ିକ ସତ୍ୟ ସେଗୁଡ଼ିକୁ ଚିହ୍ନଟ କର ।

(i) 0 ∈ R
ସମାଧାନ:
T

(ii) √16 ∈ Q
ସମାଧାନ:
T

(iii) √5 ∈ R
ସମାଧାନ:
T

(iv) -0 = 0
ସମାଧାନ:
T

(v) -π ∈ Q
ସମାଧାନ:
F

(vi) 2π ∈ Q’
ସମାଧାନ:
T

(vii) 2 + √2 ∈ Q
ସମାଧାନ:
F

(viii) Q ⊂ R
ସମାଧାନ:
T

(ix) π ∈ Q’
ସମାଧାନ:
T

(x) Q ∪ Q’ = R
ସମାଧାନ:
T

(xi) Q ⊂ Q’
ସମାଧାନ:
F

(xii) R – Q = Q’
ସମାଧାନ:
T

(xiii) √2 ଓ √3 ମଧ୍ୟରେ ଅସୀମ ସଂଖ୍ୟକ ଅପରିମେୟ ସଂଖ୍ୟା ବିଦ୍ୟାମନ ।
ସମାଧାନ:
F

(xiv) 0.01001000100001.. ଏକ ପରିମେୟ ସଂଖ୍ୟା
ସମାଧାନ:
 (F) କାରଣ : ଏହି ଅସରନ୍ତି ଦଶମିକ ସଂଖ୍ୟାଟି ପୌନଃପୁନିକ ନୁହେଁ ।

(xv) x ∈ R ହେଲେ \(\mathrm{x} \cdot \frac{1}{\mathrm{x}}\) = 1
ସମାଧାନ:
(F) (xv) (F) କାରଣ : x = 0 ହେଲେ ଏହା ସତ୍ୟ ନୁହେଁ ।

(xvi) ଦୁଇଗୋଟି ପରିମେୟ ସଂଖ୍ୟାର ଯୋଗଫଳ ପରିମେୟ ।
ସମାଧାନ:
(T) ଦୁଇଗୋଟି ପରିମେୟ ସଂଖ୍ୟାର ଯୋଗ ସଂବୃତ୍ତି ନିୟମ ପାଳନ କରେ, ତେଣୁ ପରିମେୟ ସଂଖ୍ୟାର ଯୋଗଫଳ ପରିମେୟ ସଂଖ୍ୟା ।

(xvii) ଦୁଇଟି ପରିମେୟ ସଂଖ୍ୟାର ଯୋଗଫଳ ଅପରିମେୟ ।
ସମାଧାନ:
 (F) (ଏହା ସାର୍ବଜନୀନ ସତ୍ୟ ନୁହେଁ ।)

(xviii) ଦୁଇଟି ଅପରିମେୟ ସଂଖ୍ୟାର ଯୋଗଫଳ ପରିମେୟ ।
ସମାଧାନ:
(F) (ଏହା ମଧ୍ୟ ସାର୍ବଜନନୀ ସତ୍ୟ ନୁହେଁ ।)

(xix) ଦୁଇଟି ଅପରିମେୟ ସଂଖ୍ୟାର ଗୁଣଫଳ ଅପରିମେୟ ।
ସମାଧାନ:
(F) (ଏହା ସାର୍ବଜନୀନ ସତ୍ୟ ନୁହେଁ ।)

(xx) π ସହ ଯେକୌଣସି ବାସ୍ତବ ସଂଖ୍ୟା ଯୋଗ କଲେ ଯୋଗଫଳ ଅପରିମେୟ ।
ସମାଧାନ:
F

Question 3.
ନିମ୍ନଲିଖ ରାଶିମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁ ସଂଖ୍ୟାଗୁଡ଼ିକ ପରିମେୟ ଓ କେଉଁଗୁଡ଼ିକ ଅପରିମେୟ ଲେଖ ।

(i) 3
ସମାଧାନ:
ପରିମେୟ ରାଣି

(ii) \(\frac{1}{2}\)
ସମାଧାନ:
ପରିମେୟ ରାଣି

(iii) -10
ସମାଧାନ:
ପରିମେୟ ରାଣି

(iv) √81
ସମାଧାନ:
ପରିମେୟ ରାଣି

(v) \(\frac{22}{7}\)
ସମାଧାନ:
ପରିମେୟ ରାଣି

(vi) π
ସମାଧାନ:
ଅପରିମେୟ ରାଣି

(vii) \(\frac{\sqrt{3}}{2}\)
ସମାଧାନ:
ଅପରିମେୟ ରାଣି

(viii) \(\frac{1}{\sqrt{2}}\)
ସମାଧାନ:
ଅପରିମେୟ ରାଣି

(ix) 0 7
ସମାଧାନ:
ପରିମେୟ ରାଣି

(x) \(0 . \overline{7}\)
ସମାଧାନ:
ପରିମେୟ ରାଣି

(xi) √0.7
ସମାଧାନ:
ଅପରିମେୟ ରାଣି

(xii) 0.07007000700007….
ସମାଧାନ:
ଅପରିମେୟ ରାଣି

Question 4.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର :

(i) 2ର ଗୁଣନାତ୍ମକ ବିଲୋମୀ _______ ।
ସମାଧାନ:
\(\frac{1}{2}\)

(ii) √2 ର ଗୁଣନାତ୍ମକ ବିଲୋମୀ _____ ।
ସମାଧାନ:
\(\frac{1}{\sqrt{2}}\)

(iii) √2 ର ଯୋଗାତ୍ମକ ବିଲୋମୀ _____ ।
ସମାଧାନ:
-√2

(iv) πର \(\frac{22}{7}\) ଏଳ ମାନ ଅଟେ ।
ସମାଧାନ:
ଆସନୄ

(v) 4 – √3 ର ଗୁଣନାତ୍ମକ ବିଲୋମୀ _____ ।
ସମାଧାନ:
√3 – 4

(vi) _____ ର ଗୁଣନାତ୍ମକ ବିଲୋମୀ ଓ ଯୋଗାତ୍ମକ ବିଲୋମୀର ସମଷ୍ଟି ଶୂନ ଅଟେ ।
ସମାଧାନ:
1 ଳିମୂ‍। -1

(vii) _____ px = py ହେଲ x = y ହେବ କେବଳ ଯଦି
ସମାଧାନ:
p ≠ 0

(viii) Q ∪ Q’ = _____ ।
ସମାଧାନ:
R

(ix) -π ର ପରମ ମାନ _____ ।
ସମାଧାନ:
π

(x) x = 0 ହେଲେ | x | ର ମାନ _____ ।
ସମାଧାନ:
0

Question 5.
‘କ’ ସ୍ତମ୍ଭରେ ଥ‌ିବା ସଂଖ୍ୟାମାନଙ୍କୁ ‘ଖ’ ସ୍ତମ୍ଭରେ ଥ‌ିବା ପଦ ସହ (ଅର୍ଥ ଭିଭିକ) ମଳାଇ ରଖ ।

‘କ’	‘ଖ’
(i) 0	(i) ଗୁଣନାତ୍ମକ ବିଲୋମୀ
(ii)  1	(ii)  ମୌଳିକ ସଂଖ୍ୟା
(iii) √2	(iii) ଅପରିମେୟ ସଂଖ୍ୟା
(iv) 5	(iv) ଯୁଗ୍ମ ସଂଖ୍ୟା
(v) 6	(v) ଆସନ୍ନମାନ \(\frac{22}{7}\)
(vi)  \(0 . \overline{7}\)	(vi)  ଯୋଗାତ୍ମକ ବିଲୋମୀ
(vii) x ଓ -x	(vii) ଯୋଗାତ୍ମକ ଅଭେଦ
(viii) 2 ଓ \(\frac{1}{2}\)	(viii) ଭଗ୍ନସଂଖ୍ୟା \(\frac{p}{q}\)
(ix) π	(ix)  ଗୁଣନାତ୍ମକ ଅଭେଦ

ସମାଧାନ:

‘କ’	‘ଖ’
(i) 0	(vii) ଯୋଗାତ୍ମକ ଅଭେଦ
(ii)  1	(ix)  ଗୁଣନାତ୍ମକ ଅଭେଦ
(iii) √2	(iii) ଅପରିମେୟ ସଂଖ୍ୟା
(iv) 5	(ii)  ମୌଳିକ ସଂଖ୍ୟା
(v) 6	(iv) ଯୁଗ୍ମ ସଂଖ୍ୟା
(vi)  \(0 . \overline{7}\)	(viii) ଭଗ୍ନସଂଖ୍ୟା \(\frac{p}{q}\)
(vii) x ଓ -x	(vi)  ଯୋଗାତ୍ମକ ବିଲୋମୀ
(viii) 2 ଓ \(\frac{1}{2}\)	(i) ଗୁଣନାତ୍ମକ ବିଲୋମୀ
(ix) π	(v) ଆସନ୍ନମାନ \(\frac{22}{7}\)

Question 6.
ନିମ୍ନଲିଖତ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଗୋଟିଏ ଲେଖାଏଁ ଉଦାହରଣ ଦିଅ ।

(i) x ଓ y ଅପରିମେୟ ମାତ୍ର x + y ପରିମେୟ
ସମାଧାନ:
x ଓ y ଅପରିମେୟ ମାତ୍ର x + y ପରିମେୟ
ମନେକର x = 2 + √3 ଏବଂ y = 2 – √3
⇒ x + y = 2+ √3 + 2 – √3
x + y = 4 (ପରିମେୟ)

(ii) x ଓ y ଅପରିମେୟ ଓ x + y ଅପରିମେୟ
ସମାଧାନ:
x ଓ y ଅପରିମେୟ ମାତ୍ର x + y ଅପରିମେୟ
ମନେକର x = √3 + 1 ଓ y = √3 + 1
x + y = √3 + 1 + √3 – 1 = 2√3 ଅପରିମେୟ

(iii) x ଓ y ଅପରିମେୟ ମାତ୍ର x – Y ପରିମେୟ
ସମାଧାନ:
x ଓ y ଅପରିମେୟ ମାତ୍ର x – Y ପରିମେୟ
ମନେକର x = √3 + 4 ଏବଂ y = √3 – 4
∴ x – y = (√3 + 4) − (√3 – 4)
= √3 + 4 – √3 + 4 = 8 (ପରିମେୟ)

(iv) x ଓ y ଅପରିମେୟ ମାତ୍ର xy ପରିମେୟ
ସମାଧାନ:
x ଓ y ଅପରିମେୟ ମାତ୍ର xy ପରିମେୟ
ମନେକର x = √3 + 1, y = √3 – 1
⇒ xy = (√3 + 1)(√3 − 1) = (√3)² – (1)² = 3 – 1 = 2 (ପରିମେୟ)

(v) x ଓ y ଅପରିମେୟ ଓ xy ଅପରିମେୟ
ସମାଧାନ:
x ଓ y ଅପରିମେୟ ମାତ୍ର xy ଅପରିମେୟ
ମନେକର x = √2, y = √3
⇒ xy = √2 × √3 = √6 (ଅପରିମେୟ)

(vi)  x ଓ y ଅପରିମେୟ ମାତ୍ର \(\frac{x}{y}\) ପରିମେୟ
ସମାଧାନ:
x ଓ y ଅପରିମେୟ ମାତ୍ର \(\frac{x}{y}\) ପରିମେୟ
ମନେକର x = 2√3, y = 3√3
⇒ \(\frac{x}{y}=\frac{2 \sqrt{3}}{3 \sqrt{3}}=\frac{2}{3}\) (ପରିମେୟ)

(vii) x ଓ y ଅପରିମେୟ ଓ \(\frac{x}{y}\) ଅପରିମେୟ
ସମାଧାନ:
x ଓ y ଅପରିମେୟ ଓ \(\frac{x}{y}\) ଅପରିମେୟ
ମନେକର x = √6 ଓ y = √3
⇒ x = \(\frac{\sqrt{6}}{\sqrt{3}}\) = √2 (ଅପରିମେୟ)

Question 7.
ନିମ୍ନଲିଖୂତ ପ୍ରଶ୍ନମାନଙ୍କ ଉତ୍ତର ଦିଅ ।

(i) କେଉଁ ବାସ୍ତବ ସଂଖ୍ୟା ତା’ ନିଜର ଯୋଗାତ୍ମକ ବିଲୋମୀ ଅଟେ ?
ସମାଧାନ:
0 = -0 ଏବଂ 0 ∈ R । ତେଣୁ ଉତ୍ତର 0 ଅଟେ ।

(ii) କେଉଁ ବାସ୍ତବ ସଂଖ୍ୟା ତା’ ନିଜର ଗୁଣନାତ୍ମକ ବିଲୋମୀ ଅଟେ ?
ସମାଧାନ:
1 = \(\frac{1}{1}\) ଏବଂ – 1 = \(\frac{1}{-1}\) ତେଣୁ ଉତ୍ତର I ଏବଂ – 1 ଏଠାରେ {1, – 1} e R । ତେଣୁ ଉତ୍ତର 1 କିମ୍ବା (-1) ।

(iii) a x 0 = b x 0 ହେଲେ ସର୍ବଦା a = b ହେବ କି ? କାରଣ ସହ ଉତ୍ତର ଦିଅ ।
ସମାଧାନ:
a × 0 = b × 0 ଏହା ସର୍ବଦା a = b ହେବ ନାହିଁ । (କାରଣ 15 × 0 = 28 × 0 ∴ 15 ≠ 28)

(iv) ଦୁଇଗୋଟି ଅପରିମେୟ ସଂଖ୍ୟା ଲେଖ ଯେପରି ସେମାନଙ୍କ ଗୁଣଫଳ ପରିମେୟ ମାତ୍ର ଯୋଗଫଳ ଅପରିମେୟ ହେବ ।
ସମାଧାନ:
ମନେଳର x = (√3 + 1), y = (√3 – 1)
ସଂଖ୍ୟ‍।ଦୁୟର ଗୁଣଫଳ xy = (√3 + 1) (√3 − 1) = (√3)² − 1² = 3 − 1 = 2 (ପରିମେୟ )
ସଂଖ୍ୟ‍।ଦୁୟର ଯୋଗଫଳ x + y = √3 + 1 + √3 − 1 = √3 + √3 = 2√3 (ଅପରିମେୟ)

(v) ଦୁଇଗୋଟି ଅପରିମେୟ ସଂଖ୍ୟା ଲେଖ ଯେପରି ସେମାନଙ୍କ ଯୋଗଫଳ ପରିମେୟ ମାତ୍ର ଗୁଣନଫଳ ଅପରିମେୟ ହେବ ।
ସମାଧାନ:
ମନେଳର x = 2 – √3, y = √3
x + y = 2 – √3 + √3 = 2 (ପରିମେୟ )
xy = ( 2 – √3) √3 = 2√3 – 3 (ଅପରିମେୟ)‍।

(vi) ଏକ ପରିମେୟ ଭଗ୍ନ ସଂଖ୍ୟ ଦଶମିକ ଓ ଏକ ଅପରିମେୟ ସଂଖ୍ୟାର ଦଶମିକ ରୂପରେ ପାର୍ଥକ୍ୟ କ’ଣ ଥାଏ ?
ସମାଧାନ:
ପରିମେୟ ଭଗ୍ନସଂଖ୍ୟାର ଦଶମିକ ରୂପ ସସୀମ ଦଶମିକ ସଂଖ୍ୟା ଓ ପୌନଃପୁନିକ ଦଶମିକ ସଂଖ୍ୟା । ଏକ ଅପରିମେୟ ସଂଖ୍ୟାର ଦଶମିକ ରୂପ ଅସୀମ ଦଶମିକ ସଂଖ୍ୟା ମାତ୍ର ଅଣପୌନଃପୁନିକ ଅଟେ ।

Question 8.
ନିମ୍ନଲିଖ ସଂଖ୍ୟାମାନଙ୍କ ଯୋଗଫଳ ସ୍ଥିର କର ‍।

(i) √18 ଓ √72
ସମାଧାନ:
√18 + √72 = \(\sqrt{9 \times 2}+\sqrt{36 \times 2}\) = 3√ + 6√2 = (3+6) √2=9√2

(ii) 3√2 ଓ 7√2
ସମାଧାନ:
3√2 + 7√2 = (3 + 7) √2 = 10√2

(iii) √5 ଓ -√5
ସମାଧାନ:
√5 + (-√5) = √5 – √5 = 0

(iv) √75, √108 ଓ √147
ସମାଧାନ:
√75 + √108 + √147 = \(\sqrt{25 \times 3}+\sqrt{36 \times 3}+\sqrt{49 \times 3}\)
= 5√3 + 6√3 + 7√3 = (5 + 6 + 7) √3 = 18√3

Question 9.
ନିମ୍ନଲିଖ ସଂଖ୍ୟାମାନଙ୍କର ଗୁଣଫଳ ସ୍ଥିର କର ।

(i) √5 ଓ √2
ସମାଧାନ:
√5 × √2 = \(\sqrt{5 \times 2}\) = √10

(ii) √20 ଓ √5
ସମାଧାନ:
√20 × √5 = \(\sqrt{20 \times 5}\) = √100 = 10

(iii) (3 + √2) ଓ (3 – √2)
ସମାଧାନ:
(3 + √2)(3 – √2) = 3² − (√2)² = 9 – 2 = 7

(iv) √12, √45 ଓ √15
ସମାଧାନ:
√12 × √45 × √15 = \(\sqrt{12 \times 45 \times 15}=\sqrt{2 \times 2 \times 3 \times 3 \times 3 \times 5 \times 3 \times 5}\)
= 2 × 3 × 3 × 5 = 90

Question 10.
ନିମ୍ନଲିଖତ ରାଶିମାନଙ୍କୁ x ସହ ଗୁଣନ କଲେ ଯଦି ଗୁଣଫଳ 1 (ଏକ) ତେବେ x ର ମୂଲ୍ୟ ନିର୍ଣ୍ଣୟ କର ଯେପରିକି xର ହର ଏକ ପୂର୍ବ ସଂଖ୍ୟା ହେବ ।

(i) √3
ସମାଧାନ:
√3 × x = 1 ⇒ x = \(\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{\sqrt{3} \times \sqrt{3}}=\frac{\sqrt{3}}{3}\)

(ii) 3√2
ସମାଧାନ:
3√2 × x = 1 ⇒ x = \(\frac{1}{3 \sqrt{2}}=\frac{\sqrt{2}}{3 \sqrt{2} \times \sqrt{2}}=\frac{\sqrt{2}}{6}\)

(iii) 2 + √3
ସମାଧାନ:
(2 + √3) × x = 1 ⇒ x = \(\frac{1}{2+\sqrt{3}}\)
⇒ x = \(\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}=\frac{2-\sqrt{3}}{(2)^2-(\sqrt{3})^2}=\frac{2-\sqrt{3}}{4-3}\) = 2 – √3
∴ xର ଗୁଲ୍ୟ = 2 – √3

(iv) √5 – 1
ସମାଧାନ:
(√5 – 1) × x = 1 ⇒ x = \(\frac{1}{\sqrt{5}-1}\)
⇒ x = \(\frac{\sqrt{5}+1}{(\sqrt{5}-1)(\sqrt{5}+1)}=\frac{\sqrt{5}+1}{(\sqrt{5})^2-(1)^2}=\frac{\sqrt{5}+1}{5-1}=\frac{\sqrt{5}+1}{4}\)

(v) √3 + √2
ସମାଧାନ:
(√3 + √2) × x = 1 ⇒ x = \(\frac{1}{\sqrt{3}+\sqrt{2}}\)
⇒ x = \(\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}=\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3})^2-(\sqrt{2})^2}=\frac{\sqrt{3}-\sqrt{2}}{3-2}\) = √3 – √2
∴ xର ଗୁଲ୍ୟ = √3 – √2
ବି.ଦ୍ର. : – : ପ୍ରତ୍ୟେକର ଗୁଣନାତ୍ମକ ବିଲୋମୀକୁ ପରିମେୟ ହର ବିଶିଷ୍ଟ ରାଶିରେ ପରିଣତ କରାଯାଇଛି ।

Question 11.
0.303003000300003….. ଦଶମିକ ରାଶିଟି ପରିମେୟ କି ଅପରିମେୟ କାରଣ ସହ ଲେଖ ।
ସମାଧାନ:
0.303003000300003….. ରାଶିଟି ଅପରିମେୟ ଅଟେ ।
କାରଣ – ଉକ୍ତ ଦଶମିକ ଭଗ୍ନାଂଶ ଅସୀମ ଓ ଅଣପୌନଃପୁନିକ ଦଶମିକ ସଂଖ୍ୟା ଅଟେ ।

Question 12.
P ଓ Q ବିନ୍ଦୁଦ୍ଵୟ ସଂଖ୍ୟାରେଖାରେ ନିମ୍ନଲିଖିତ ସଂଖ୍ୟା ଯୋଡ଼ି ଦ୍ଵାରା ସୂଚିତ ହେଲେ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ର ପାଇଁ PQ ଦୂରତା ନିର୍ଣ୍ଣୟ କର ।
P ଓ Qଚ ଘାନାଢ ଯଥାକୁମେ a ଓ b ହେଲେ PQ = |a – b|

(i) 8 ଓ 15
ସମାଧାନ:
PQ = |8 – 15| = |-7| = 7

(ii) -4 ଓ 3.2
ସମାଧାନ:
PQ = |- 4 – 3.2| = |-7.2| = 7.2

(iii) -3.7 ଓ -6.1
ସମାଧାନ:
PQ =|-3.7 – (-6.1)| = |-3.7 + 6.1| = |2.4| = 2.4

(iv) π ଓ -3π
ସମାଧାନ:
PQ = |π – (-3π)| = |π + 3π| = |4π| = 4π

Question 13.
ନିମ୍ନଲିଖ ରାଶିମାନଙ୍କୁ ପରିମେୟ ହର ବିଶିଷ୍ଟ ରାଶିରେ ପ୍ରକାଶ କର ।

(i) \(\frac{2}{3(\sqrt{3}+2)}\)
ସମାଧାନ:

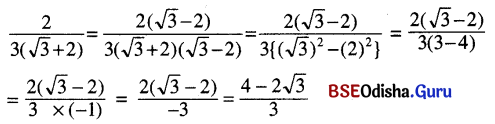
(ii) \(\frac{2}{1+\sqrt{2}}\)
ସମାଧାନ:
\(\frac{2}{1+\sqrt{2}}=\frac{2(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}=\frac{2(\sqrt{2}-1)}{(\sqrt{2})^2-(1)^2}=\frac{2(\sqrt{2}-1)}{2-1}\) = 2(√2 – 1)

(iii) \(\frac{2}{\sqrt{2}+3}\)
ସମାଧାନ:
\(\frac{2}{\sqrt{2}+3}=\frac{2}{3+\sqrt{2}}=\frac{2(3-\sqrt{2})}{(3+\sqrt{2})(3-\sqrt{2})}=\frac{2(3-\sqrt{2})}{(3)^2-(\sqrt{2})^2}=\frac{2(3-\sqrt{2})}{9-2}=\frac{2(3-\sqrt{2})}{7}\)

(iv) \(\frac{1}{1+\sqrt{2}}\)
ସମାଧାନ:
\(\frac{1}{1+\sqrt{2}}=\frac{1}{\sqrt{2}+1}=\frac{1(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}=\frac{(\sqrt{2}-1)}{(\sqrt{2})^2-(1)^2}=\frac{(\sqrt{2}-1)}{2-1}\) = √2 – 1

(v) \(\frac{5}{3-\sqrt{2}}\)
ସମାଧାନ:
\(\frac{5}{3-\sqrt{2}}=\frac{5(3+\sqrt{2})}{(3-\sqrt{2})(3+\sqrt{2})}=\frac{5(3+\sqrt{2})}{(3)^2-(\sqrt{2})^2}=\frac{5(3+\sqrt{2})}{9-2}=\frac{5(3+\sqrt{2})}{7}\)

(vi) \(\frac{1+\sqrt{2}}{\sqrt{3}+\sqrt{2}}\)
ସମାଧାନ:

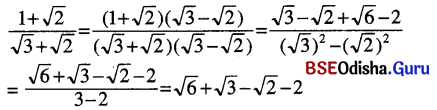
(vii) \(\frac{\sqrt{2}-1}{\sqrt{5}-\sqrt{2}}\)
ସମାଧାନ:

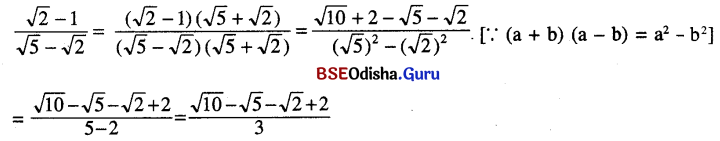
(viii) \(\frac{1}{1+\sqrt{2}+\sqrt{3}}\)
ସମାଧାନ:

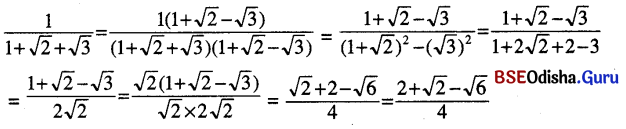
(ix) \(\frac{\sqrt{2}+\sqrt{3}}{\sqrt{2}+\sqrt{3}+\sqrt{5}}\)
ସମାଧାନ:

Question 14.
ସରଳ ଜର :

(i) \(\frac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}+\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}\)
ସମାଧାନ:

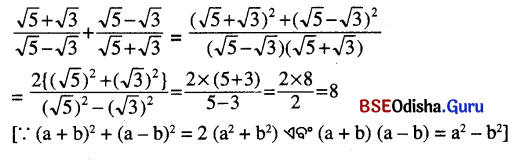
(ii) \(\frac{\sqrt{7}-\sqrt{5}}{\sqrt{7}+\sqrt{5}}+\frac{\sqrt{7}+\sqrt{5}}{\sqrt{7}-\sqrt{5}}\)
ସମାଧାନ:

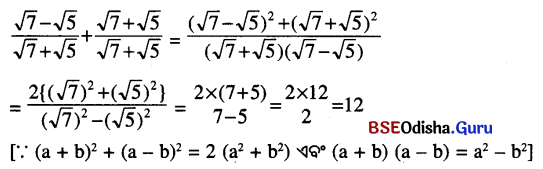
Question 15.
a ଓ b ପରିମେୟ ସଂଖ୍ୟା ହେଲେ ନିମ୍ନଲିଖତ କ୍ଷେତ୍ରରେ ସେମାନଙ୍କ ମାନ ନିର୍ଣ୍ଣୟ କର ।

(i) \(\frac{\sqrt{3}-1}{\sqrt{3}+1}\) = a + b√3
ସମାଧାନ:

(ii) \(\frac{4+\sqrt{5}}{4-\sqrt{5}}\) = a + b√5
ସମାଧାନ:

(iii) \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{8}}\) = a + b√6
ସମାଧାନ:

Question 16.
ସଂଖ୍ୟାରେଖା ଅଙ୍କନ କରି କମ୍ପାସ୍ ଓ ସ୍କେଲ୍‌ର ବ୍ୟବହାରଦ୍ୱାରା ନିମ୍ନଲିଖତ ସଂଖ୍ୟାମାନଙ୍କୁ ସଂଖ୍ୟାରେଖାରେ ଚିହ୍ନଟ କର ।

(i) \(\frac{3}{5}\)
ସମାଧାନ:
ଏଠାରେ \(\frac{3}{5}\) < 1 ଏବଂ \(\frac{3}{5}\) > 0, ଅର୍ଥାତ୍ 0 < \(\frac{3}{5}\) < 1।

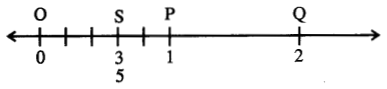
OP = PQ ହେବ ।
∴ \(\frac{3}{5}\) ର ସୂଚକ ବିନ୍ଦୁଟି ଠ ର ଡାହାଣକୁ ଏବଂ P ବିନ୍ଦୁର ବାମକୁ ରହିବ । ଅର୍ଥାତ୍ ସୂଚକ ବିନ୍ଦୁ, OP ରେଖାଖଣ୍ଡ ଉପରେ
0 ଏବଂ 1 ର ମଧ୍ୟବର୍ତୀ ଅଂଶକୁ ସମାନ ପାଞ୍ଚଭାଗ କରି S ବିନ୍ଦୁ ଚିହ୍ନଟ କର, ଯାହା \(\frac{3}{5}\) ର ସୂଚକ ବିନ୍ଦୁ ହେବ ।

(ii) 1 \(\frac{1}{3}\)
ସମାଧାନ:

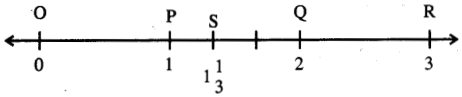
ଏଠାରେ 1 \(\frac{1}{3}\) < 2 ଅର୍ଥାତ୍ 0 < \(\frac{4}{3}\) < 2
∴ \(\frac{4}{3}\) ର ସୂଚକ ବିନ୍ଦୁଟି O ର ଡାହାଣକୁ \(\overline{\mathrm{PQ}}\) ରେଖାଖଣ୍ଡ ଉପରେ ରହିବ । PQ ର ମଧ୍ୟବର୍ତୀ ଅଂଶକୁ ସମାନ ତିନିଭାଗ କରି S ବିନ୍ଦୁ ଚିହ୍ନଟ କର ଯାହା \(\frac{4}{3}\) ର ସୂଚକ ବିନ୍ଦୁ ହେବ ।

(iii) √2 – 1
ସମାଧାନ:
ଆମେ ଜାଣିଛେ ଯେ 1 < 2 < 4
⇒ 1 < √2 < 2 ⇒ 1 – 1 < √2 – 1 < 2 – 1 ⇒ 0 <, 2 – 1 < 1

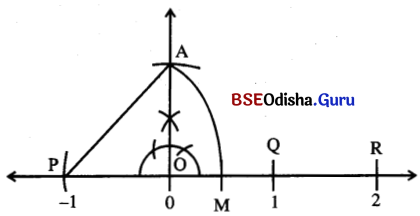
∴ √2 – 1କୁ ସୂଚାଉଥୁବା ବିନ୍ଦୁଟି ସଂଖ୍ୟାରେଖାର 0 ଓ 1 ଦ୍ଵୟକୁ ସୂଚାଉଥବା ବିଦୁ୍ୟଦ୍ଵୟ ମଧ୍ଯରେ ଅବସ୍ଥାନ କରିବ ଅର୍ଥାତ୍ ସୂଚକ ବିନ୍ଦୁଟି\(\overline{\mathrm{OQ}}\) ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ ହେବ ।
Δ AOP ସମକୋଣୀ ତ୍ରିଭୁଜରେ PO = AO = 1 ଏକକ
∴ AP = \(\sqrt{\mathrm{PO}^2+\mathrm{OA}^2}\) =√2 ଏକକ।
Pକୁ କେନ୍ଦ୍ରକରି ଓ AP ବ୍ୟାସାର୍ଦ୍ଧ ପରିମିତ ଚାପ ସଂଖ୍ୟାରେଖାକୁ M ବିନ୍ଦୁରେ ଛେଦକରୁ । ଏଠାରେ M ବିନ୍ଦୁଟି √2 – 1 ର ସୂଚକ ବିନ୍ଦୁ ।

(iv) √2 + 1
ସମାଧାନ:
ଆମେ ଜାଣିଛେ, 1 < 2 < 4
∴ 1 < √2 < 2 ⇒ 1 + 1 < √2 + 1 < 2 + 1 ⇒ 2 < √2 + 1 < 3

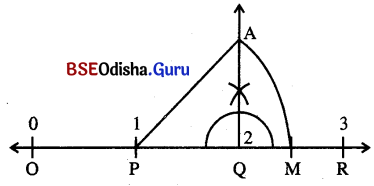
∴ √2 + 1 କୁ ସୂଚାଉଥବା ବିନ୍ଦୁଟି ସଂଖ୍ୟାରେଖାର 2 ଓ 3 ଦ୍ୱୟକୁ ସୂଚାଉଥବା ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ଯରେ ଅବସ୍ଥାନ କରିବ । ଅର୍ଥାତ୍ ସୂଚକ ବିନ୍ଦୁଟି \(\overline{\mathrm{QR}}\) ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ ହେବ ।
Δ APQ ସମକୋଣୀ A ରେ PQ = AQ = 1 ଏକକ
∴ AP = \(\sqrt{\mathrm{PQ}^2+\mathrm{AQ}^2}\) = √2 ଏକକ
P କେନ୍ଦ୍ର ଓ AP ବ୍ୟାସାର୍ଷ ପରିମିତ ଚାପ ସଂଖ୍ୟାରେଖାକୁ M ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
ଏଠାରେ M ବିନ୍ଦୁଟି √2 + 1 ର ସୂଚକ ବିନ୍ଦୁ ହେବ ।

(v) 2 + √3
ସମାଧାନ:
1 < 3 < 4 ⇒ 1 < √3 < 2
⇒ 2 + 1 < 2 + √3 < 2 + 2 ⇒ 3 < 2 + √3 < 4

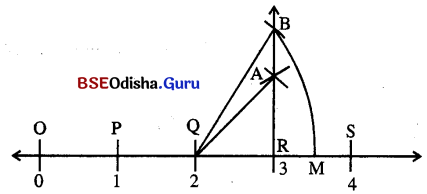
∴ 2 + √3 କୁ ସୂଚାଉଥବା ବିନ୍ଦୁଟି  3 ଓ 4 ଦ୍ୱୟକୁ ସୂଚାଉଥବା ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ଯରେ ଅବସ୍ଥାନ କରିବ । 
AQR ସମକୋଣୀ ତ୍ରିଭୁଜରେ QR = AR = 1 ଏକକ
∴ AQ = \(\sqrt{\mathrm{QR}^2+\mathrm{AR}^2}\) = √2 ଏକକ AQ = BR = √2 ଏକକ
BQR ସମକୋଣୀ A ରେ QR = 1 ଏକକ, RB = √2 ଏକକ
∴ BQ = \(\sqrt{\mathrm{QR}^2+\mathrm{BR}^2}\) = \(\sqrt{1^2+(\sqrt{2})^2}=\sqrt{1+2}\) = √3 ଏକକ
Qକୁ କେନ୍ଦ୍ରକରି ଓ BQ ବ୍ୟାସାର୍ଦ୍ଧ ପରିମିତ ଚାପ ସଂଖ୍ୟାରେଖାକୁ M ବିନ୍ଦୁରେ ଛେଦକରୁ ।
M ବିନ୍ଦୁଟି 2 + √3 ର ସୂଚକ ବିନ୍ଦୁ ।

(vi) √5
ସମାଧାନ:
ଆମେ ଜାଣିଛେ, 4 < 5 < 9 ⇒ √4 < √5 < √9 ⇒ 2 < √5 < 3
∴ √5 କୁ ସୂଚାଉଥବା ବିନ୍ଦୁଟି 2 ଓ 3 ଦ୍ଵୟକୁ ସୂଚାଉଥବା ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ୟରେ ଅବସ୍ଥାନ କରିବ ।

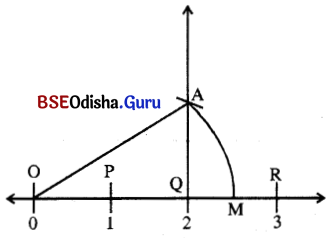
OAM ସମକୋଣୀ ତ୍ରିଭୁଜରେ OQ = 2 ଏକକ, AQ = 1 ଏକକ
OA = \(\sqrt{\mathrm{OQ}^2+\mathrm{AQ}^2}=\sqrt{2^2+1^2}=\sqrt{4+1}\) = √5 ଏକକ
ଠକୁ କେନ୍ଦ୍ରକରି ଓ OA ବ୍ୟାସାର୍ଦ୍ଧ ପରିମିତ ଚାପ ସଂଖ୍ୟାରେଖାକୁ M ନାମରେ ଛେଦକରୁ ।
M ବିନ୍ଦୁଟି √5 ର ସୂଚକ ବିନ୍ଦୁ ହେବ ।

(vii) √3 – 1
ସମାଧାନ:
ଆମେ ଜାଣିଛେ, 1 < 3 < 4 ⇒ 1 < √3 < 2
⇒ 1 – 1 < √3 – 1 < 2 − 1 ⇒ 0 < √3 − 1 < 1
∴ (√3 – 1) ର ସୂଚକ ବିନ୍ଦୁଟି ) ଓ 1 କୁ ସୂଚାଉଥବା ବିଦୁ୍ୟଦ୍ଵୟ ମଧ୍ଯରେ ଅବସ୍ଥାନ କରିବ ।

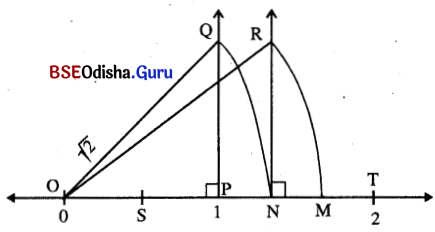
ଏଠାରେ OP = PQ = 1 ଏକକ, OQ = \(\sqrt{1^2+1^2}\) = √2 ଏକକ
ପୁନଶ୍ଚ OQ = ON = 2 ଏକକ ଓ NR = 1 ଏକକ 
∴ OR = \(\sqrt{(\sqrt{2})^2+(1)^2}=\sqrt{2+1}\) = √3 ଏକକ । OR = OM = √3 ଏକକ, SM = 1 ଏକକ ।
∴ OS = OM – SM = (√3 – 1) ଏକକ ।
⇒ (√3 – 1)ର ସୂଚକ ବିନ୍ଦୁଟି OP ଉପରିସ୍ଥ ଏବଂ S ଦ୍ଵାରା ଚିହ୍ନିତ ।

Question 17.
ସଂଖ୍ୟାରେଖାରେ ନିମ୍ନ ସଂଖ୍ୟାମାନଙ୍କୁ ସ୍ଥାପନ କରି କେଉଁଟି ବୃହତ୍ତର ସ୍ଥିର କର ।

(i)  -√3 ଓ -√2
ସମାଧାନ:
 -√3 ଓ −√2 ର ମାନ – 2 ଓ – 1 ମଧ୍ୟରେ ଅବସ୍ଥିତ ।
ବି.ଦ୍ର. – ସଂଖ୍ୟାରେଖା ଉପରେ ବାମପାର୍ଶ୍ବ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଦକ୍ଷିଣ ପାର୍ଶ୍ଵର ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କଠାରୁ କ୍ଷୁଦ୍ରତର ।

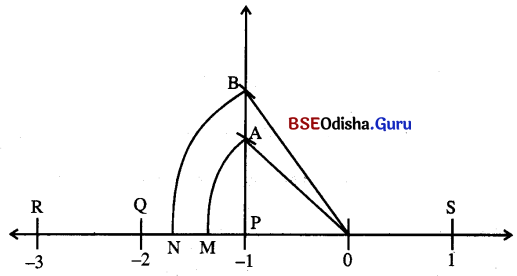
AOP ସମକୋଣୀ ତ୍ରିଭୁଜରେ OP = PA = 1 ଏକକ
AO = \(\sqrt{\mathrm{OP}^2+\mathrm{AP}^2}=\sqrt{(1)^2+(1)^2}\) = √2
ଠକୁ କେନ୍ଦ୍ରକରି \(\overline{\mathrm{AP}}\) ବ୍ୟାସାର୍ଦ୍ଧ ପରିମିତ ଚାପ ସଂଖ୍ୟାରେଖାକୁ M ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
∴ M ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ √2 ହେବ ।
BOP ସମକୋଣୀ ତ୍ରିଭୁଜରେ OM = PB = √2 ଏକକ ।
BO = \(\sqrt{\mathrm{BP}^2+\mathrm{PO}^2}=\sqrt{(\sqrt{2})^2+1^2}=\sqrt{2+1}\) =√3
ଠକୁ କେନ୍ଦ୍ରକରି OB ବ୍ୟାସାର୍ଦ୍ଧ ପରିମିତ ଚାପ ସଂଖ୍ୟାରେଖାକୁ N ବିନ୍ଦୁରେ ଛେଦକରୁ ।
N ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ √3 ହେବ ।
ଯେହେତୁ M ବିନ୍ଦୁଟି Nର ଦକ୍ଷିଣପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ \(\stackrel{\leftrightarrow}{\mathrm{OR}}\) ଉପରିସ୍ଥ – √2> -√3 ।

(ii) \(\frac{3}{4}\) ଓ \(\frac{2}{3}\)
ସମାଧାନ:
\(\frac{3}{4}=\frac{3 \times 3}{4 \times 3}=\frac{9}{12}, \frac{2}{3}=\frac{2 \times 4}{3 \times 4}=\frac{8}{12}\)
(ଏହି ବିନ୍ଦୁଦ୍ଵୟ ସଂଖ୍ୟାରେଖାର 0 ଓ 1 ଦ୍ଵୟକୁ ସୂଚାଉଥ‌ିବା ବିଦୁ୍ୟଦ୍ଵୟ ମଧ୍ଯରେ ଅବସ୍ଥାନ କରିବ ।)

ସଂଖ୍ୟାରେଖା ଉପରିସ୍ଥ OM = \(\frac{9}{12}=\frac{3}{4}\), ON = \(\frac{8}{12}=\frac{2}{3}\)
ଯେହେତୁ M ବିନ୍ଦୁଟି Nର ଦକ୍ଷିଣ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ତେଣୁ OM > ON ⇒ \(\frac{3}{4}\) > \(\frac{2}{3}\)

(iii) √2 ଓ 1 \(\frac{1}{2}\)
ସମାଧାନ:
√2 ଓ 1 ଏହି ବିନ୍ଦୁଦ୍ଵୟ ସଂଖ୍ୟାରେଖାର 1 ଓ 2 ଦ୍ଵୟକୁ ସୂଚାଉଥିବା ବିଦୁ୍ୟଦ୍ଵୟ ମଧ୍ଯରେ ଅବସ୍ଥାନ କରିବ ।

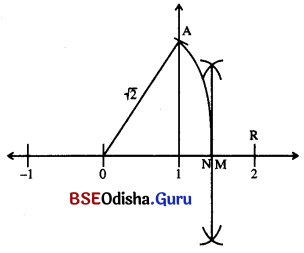
ସଂଖ୍ୟାରେଖା ଉପରିସ୍ଥ OP = AP = 1 ଏକକ
APO ସମକୋଣୀ ତ୍ରିଭୁଜରେ AO
= \(\sqrt{\mathrm{OP}^2+\mathrm{AP}^2}=\sqrt{1^2+1^2}\) = √2 ଏକକ ।
ଠକୁ କେନ୍ଦ୍ରକରି OA ବ୍ୟାସାର୍ଦ୍ଧ ପରିମିତ ଚାପ ସଂଖ୍ୟାରେଖାକୁ
N ବିନ୍ଦୁରେ ଛେଦକରୁ । ON = √2 ଏକକ ।
PR କୁ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରାଯାଉ ଏବଂ PR ର ମଧ୍ୟବିନ୍ଦୁ M ହେବ ।
OM = 1 \(\frac{1}{2}\) ଏକକ । ଯେହେତୁ M ବିନ୍ଦୁଟି Nର ଦକ୍ଷିଣ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ।
∴ OM > ON ⇒ 1 \(\frac{1}{2}\) > √2

(iv) 1.7 ଓ √3
ସମାଧାନ:
1.7 ଓ √3 ଏହି ବିନ୍ଦୁଦ୍ଵୟ ସଂଖ୍ୟାରେଖାର 1 ଓ 2 ମଧ୍ଯରେ ଅବସ୍ଥିତ ।

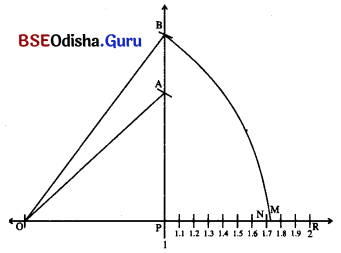
ସଂଖ୍ୟାରେଖା ଉପରିସ୍ଥ OP = PA = 1 ଏକକ ।
AOP ସମକୋଣୀ ତ୍ରିଭୁଜର କଣ୍ଠ OA
= \(\sqrt{\mathrm{OP}^2+\mathrm{PA}^2}=\sqrt{1^2+1^2}\) = √2 ଏକକ ।
ପୁନଶ୍ଚ PB = OA = √2 ଏକକ ଏବଂ OP = 1 ଏକକ ।
OB = OP² + PB² = 1² + (√2)² = √3 ଏକକ ।
OB ପରିମିତ ବ୍ୟାସାର୍ଦ୍ଧ ଚାପନେଇ ଅଙ୍କନ କଲେ ତାହା
\(\stackrel{\leftrightarrow}{\mathrm{OR}}\) କୁ M ବିନ୍ଦୁରେ ଛେଦ କରିବ । OM = √3 ଏକକ ।
PR କୁ ଦଶଟି ସମାନ ଅଂଶରେ ବିଭକ୍ତକଲେ PN = 1.7 ଏକକ ହେବ ।
M ବିନ୍ଦୁ Nର ଦକ୍ଷିଣ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ। ⇒ PM > PN ⇒ √3 > 1.7

Question 18.
ସରଳ କର :
\(\left|\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}-\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}+\frac{1}{\sqrt{2}+1}-\frac{1}{\sqrt{2}-1}\right|\)
ସମାଧାନ:

Question 19.
ଉଦାହରଣ ନେଇ ସତ୍ୟତା ପରୀକ୍ଷା କର । (ଯେଉଁଠାରେ x ଓ y ବାସ୍ତବ ସଂଖ୍ୟା) ।

(i) |x + y| ≤ |x| +|y|
ସମାଧାନ:
ମନେକର : x = \(\frac{2}{3}\) ଓ y = –\(\frac{1}{2}\)
ବାମ ପଷ : |x + y| = |\(\frac{2}{3}\) – \(\frac{1}{2}\)| = | \(\frac{4-3}{6}\)| = \(\frac{1}{6}\)
ଦଷିଣ ପଷ : |x| + |y| = \(\frac{2}{3}+-\frac{1}{2}=\frac{2}{3}+\frac{1}{2}=\frac{4+3}{6}=\frac{7}{6}\)
ଏଠାରେ lx + y| < lxl + lyl   …..(i)
ସେହିପରି ମନେକବ x = \(\frac{2}{3}\) ଓ y = \(\frac{1}{5}\)
ବାମପଷ : |x + y| = \(|\frac{2}{3}+\frac{1}{5}|=|\frac{10+3}{15}|=|\frac{13}{15} |\mid=\frac{13}{15}\)
ଦଷିଣ ପଷ : |x| + |y| = \(|\frac{2}{3}+\frac{1}{5}|=\frac{2}{3}+\frac{1}{5}=\frac{10+3}{15}=\frac{13}{15}\)
ଏଠାରେ lx + y| = lxl + lyl   …..(ii)
(i) ଓ (ii) ରୁ ପାଲବା |x + y| ≤ |x| + |y|
ବି.ଦ୍ର. ବାସ୍ତବ ସଂଖ୍ୟାର ଯେକୌଣସି ମାନନେଇ ପରୀକ୍ଷାକରି ପ୍ରମାଣ କରାଯାଇପାରିବ ।

(ii) |x – y| ≥ |x| – |y|
ସମାଧାନ:
ମନେକର : x = \(\frac{2}{3}\) ଓ y = –\(\frac{1}{2}\)
ବାମ ପଷ : |x – y| = \(\left|\frac{2}{3}-\left(-\frac{1}{2}\right)\right|=\left|\frac{2}{3}+\frac{1}{2}\right|=\left|\frac{4+3}{6}\right|=\frac{7}{6}\)
ଦଷିଣ ପଷ : |x| – |y| = \(||\frac{2}{3}|-|-\frac{1}{2}|=|\frac{2}{3}-\frac{1}{2}|=|\frac{4-3}{6}|=\frac{1}{6}\)
∴ ଏଠାରେ lx – y| > lxl + lyl   …..(i)
ସେହିପରି ମନେକବ x = \(\frac{2}{3}\) ଓ y = \(\frac{1}{5}\)
ବାମପଷ : |x – y| = \(|\frac{2}{3}-\frac{1}{5}|=|\frac{10-3}{15}|=\frac{7}{15}\)
ଦଷିଣ ପଷ : ||x| – |y|| =\(| |\frac{2}{3}|-|\frac{1}{5}|| \mid=|\frac{2}{3}-\frac{1}{5}|=|\frac{10-3}{15}|=|\frac{7}{15}|=\frac{7}{15}\)
∴ lx – y| = lxl – lyl   …..(ii)
(i) ଓ (ii) ରୁ ପାଲବା |x – y| ≥ |x| – |y|

Question 20.
ସରଳ କର :

(i) \(\left((\sqrt[n]{a})^{\sqrt{n}}\right)^{\sqrt{n}}\) a > 0, n ∈ N
ସମାଧାନ:
= \((\sqrt[n]{a})^n=\left(a^{\frac{1}{n}}\right)^n=a^{n \times \frac{1}{n}}\) = a¹ = a

(ii) \(\left(\sqrt[3]{3^3}\right)^{\sqrt[3]{3}}\)
ସମାଧାନ:
= \(\left\{(\sqrt[3]{3})^{\sqrt[3]{3}}\right\}^{3^{\frac{2}{3}}}=\left\{(\sqrt[3]{3})^{3^{\frac{1}{3}}}\right\}^{3^{\frac{2}{3}}}=\left(3^{\frac{1}{3}}\right)^{3^{\frac{1+2}{3}}}=\left(3^{\frac{1}{3}}\right)^{3^{\frac{1}{3}+\frac{2}{3}}}=\left(3^{\frac{1}{3}}\right)^{3^3}=3^{\frac{13}{3} \times 3}\) = 3¹ = 3

(iii) \(27^{1 \frac{1}{3}} \times \sqrt{\frac{1}{9}} \div 81^{\frac{1}{4}}\)
ସମାଧାନ:
= \(27^{\frac{4}{3}} \times \frac{1}{3} \div\left(3^4\right)^{\frac{1}{4}}\)
= \(\left(3^3\right)^{\frac{4}{3}} \times \frac{1}{3} \div 3^{4 \times \frac{1}{4}}=3^{3 \times \frac{4}{3}}\) × 3^-1 ÷ 3 = 3⁴ × 3^-1 ÷ 3 = 3^4-1-1 = 3² = 9

Question 21.
ଗୁଣଫଳ ନିଶୁଯୁ କର ।

(i) \(\left(a^{\frac{1}{2}}+b^{\frac{1}{2}}\right)\left(a^{\frac{1}{2}}-b^{\frac{1}{2}}\right)\) (a > 0, b > 0)
ସମାଧାନ:

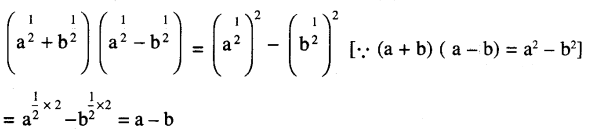
(ii) \(\left(1-a^{\frac{1}{4}}\right)\left(1+a^{\frac{1}{4}}\right)\left(1+a^{\frac{1}{2}}\right)\) (a > 0)
ସମାଧାନ:

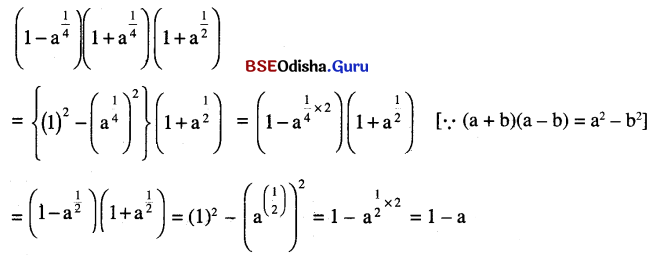
(iii) \(\left(1+a^{\frac{1}{2}}\right)\left(1+a^{\frac{1}{4}}\right)\left(1+a^{\frac{1}{8}}\right)\left(1+a^{\frac{1}{16}}\right)\left(1+a^{\frac{1}{32}}\right)\left(1-a^{\frac{1}{32}}\right)\) (a > 0)
ସମାଧାନ:

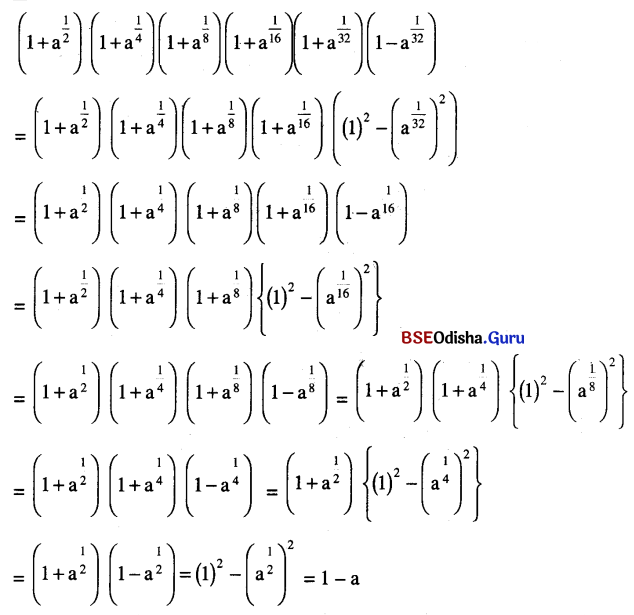
(iv) \((\sqrt[3]{x}+\sqrt[3]{y})\left(\sqrt[3]{x^2}-\sqrt[3]{x y}+\sqrt[3]{y^2}\right)\) (x > 0, y > 0)
ସମାଧାନ:

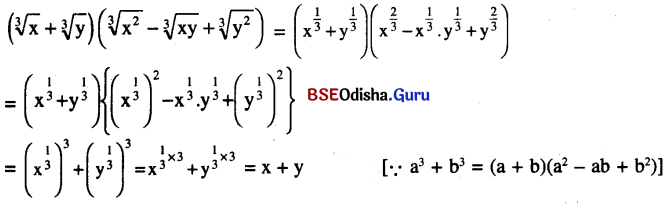
(v) \(\left(x^{-1}+x^{-\frac{1}{2}} \cdot y^{-\frac{1}{2}}+y^{-1}\right)\left(x^{-1}-x^{-\frac{1}{2}} \cdot y^{-\frac{1}{2}}+y^{-1}\right)\) (x > 0, y > 0)
ସମାଧାନ:

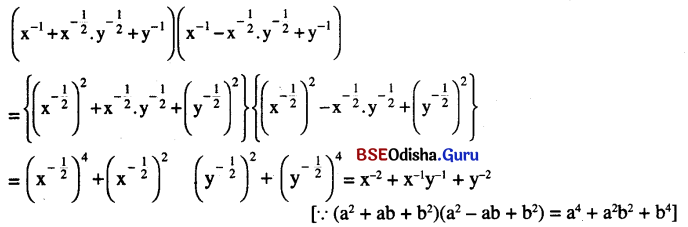
Question 22.
ସରଳ କର :

(i) \(\sqrt[3]{\mathbf{x}^{\frac{1}{2}} y^{\frac{2}{3}} z^{\frac{1}{3}}}+(x y z)^{\frac{1}{3}}\)
ସମାଧାନ:

(ii) \(\sqrt[3]{\mathbf{x}^2 \mathbf{y}^4 z^{-1}}+\sqrt{\mathbf{x}^{-\frac{2}{3}} \mathbf{y}^2 z^{-\frac{1}{3}}}\) (x > 0, y > 0, z > 0)
ସମାଧାନ:

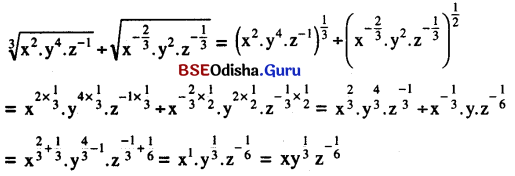
Question 23.
{x, y, z, a, b, c} ⊂ R ଓ x > 0, y > 0, z > 0 ହେଲେ ପ୍ରମାଣ କର ଯେ

(i) \(\sqrt{\mathbf{x}^{-1} y} \times \sqrt{\mathbf{y}^{-1} z} \times \sqrt{\mathbf{z}^{-1} \mathbf{x}}\) = 1
ସମାଧାନ:

(ii) \(\left(\begin{array}{l}
x^a \\
x^b
\end{array}\right)^{\frac{1}{a b}} \times\left(\frac{x^b}{x^c}\right)^{\frac{1}{b c}} \times\left(\frac{x^c}{x^a}\right)^{\frac{1}{c a}}\) = 1 (a ≠ 0, b ≠ 0, c ≠ 0)
ସମାଧାନ:

(iii) \(\left(x^{\frac{1}{a-b}}\right)^{b-c} \times\left(x^{\frac{1}{b-c}}\right)^{c-a} \times\left(x^{\frac{1}{c-a}}\right)^{\mathrm{a}-\mathrm{b}}\) = 1 [a, b ଓ c [ର ମୂଲ୍ୟ ଅସମାନ]
ସମାଧାନ:

Question 24.
(i) a = \(2^3-2^{-\frac{1}{3}}\) ହେଲେ ପ୍ରମାଣ କର ଯେ, 2a³ + 6a = 3
ସମାଧାନ:

(ii) a = \(x^3-x^{-\frac{1}{3}}\) ହେଲେ ପ୍ରମାଣ କର ଯେ, a³ + 3a = x – \(\frac{1}{x}\)
ସମାଧାନ:

Question 25.
xର ମୂଲ୍ୟ ନିବୂପଶ କର‍ ।

(i) 3^x+1 = 9
ସମାଧାନ:
3^x+1 = 9
⇒ 3^x+1 = 3²
⇒ x + 1 = 2
⇒ x = 2 – 1
⇒ x = 1

(ii) 2^2x+1 = 8
ସମାଧାନ:
2^2x+1 = 8
⇒ 2^2x+1  = 2³
⇒ 2x + 1 = 3
⇒ 2x = 3 – 1
⇒ 2x = 2
⇒ x = \(\frac{2}{2}\) = 1

(iii) (√2)^2x-1 = 1
ସମାଧାନ:
(√2)^2x-1 = 1
⇒ \(2^{\frac{2 x-1}{2}}\) = 2⁰
⇒ \(\frac{2 x-1}{2}\) = 0
⇒ 2x – 1 = 0
⇒ 2x = 1
⇒ x = \(\frac{1}{2}\)

Question 26.
ବାସ୍ତବ ସଂଖ୍ୟାର ସ୍ୱୀକାର୍ଯ୍ୟ ଓ ଆଲୋଚିତ ଅନ୍ୟ ଧର୍ମଗୁଡ଼ିକୁ ନେଇ ନିମ୍ନଲିଖ୍ ଅଭେଦଗୁଡ଼ିକ ପ୍ରତିପାଦନ କର ।

(i) a(a – b) = a² – ab
ସମାଧାନ:
a(a – b) = a.a – ab (ବଶ୍ନ ନିୟମ)
= a² – ab (ସଂଞା)
∴ a(a – b) = a² – ab (ପ୍ରମାଶିଢ)

(ii) (a ± b)² = a² ± 2ab + b²
ସମାଧାନ:
(a + b)² = (a + b). (a + b) (ସଂଞା)
= a(a + b) +b(a + b) (ବଶ୍ନନ ନିୟମ)
= a.a + a.b + b.a + b.b (ବଶ୍ନନ ନିୟମ)
= a² + ab + ba+ b²  (ସଂଞା)
= a² + ab + ab+ b² (କ୍ମମବିନିମୟୀ ନିୟମ)
= a² + 2ab + b²(ସଂଞା)
(a – b)² = (a – b). (a – b) (ସଂଞା)
= a(a – b) +b(a – b) (ବଶ୍ନନ ନିୟମ)
= a.a – a.b – b.a + b.b (ବଶ୍ନନ ନିୟମ)
= a² – ab – ba + b²  (ସଂଞା)
= a² – ab – ab + b² (କ୍ମମବିନିମୟୀ ନିୟମ)
= a² – 2ab + b²(ସଂଞା)

(iii) (a + b) (a – b) = a² – b²
ସମାଧାନ:
(a + b) (a – b) = a(a – b) + b(a – b) (ବଶ୍ନନ ନିୟମ)
= a.a – a.b + b.a – b.b (ବଶ୍ନନ ନିୟମ)
= a² – ab + ba – b²(ସଂଞା)
= a² – ab + ab – b² (କ୍ମମବିନିମୟୀ ନିୟମ)
= a² – b²
∴ (a + b) (a – b) = a² – b²

(iv) (a ± b)³ = a³ ± 3a²b + 3ab² ± b³
ସମାଧାନ:
(a + b)³ = (a + b) (a + b) (a + b) (ସଂଞା)
= {a(a + b) +(a + b)} (a + b) (ବଶ୍ନନ ନିୟମ)
= (a.a + a.b + b.a + b.b) (a + b) (ସଂଞା)
= (a² + ab + ba + b²) (a + b) (ସଂଞା)
= (a² + ab + ab + b²) (a + b) (ବଶ୍ନନ ନିୟମ)
= (a² + 2ab + b²) (a + b) (ସଂଞା)
= a(a² + 2ab + b²) + b(a² + 2ab + b²) (ବଶ୍ନନ)
= a.a² + a.2ab + a.b² + b.a² + b.2ab + b.b² (ବଶ୍ନନ)
= a³ + 2a²b + 2ab² + b³ + 2ab² + b³ (ସଂଞା)
= a³ + 2a²b + ab² + ba² + 2ab² + b³ (ବଶ୍ନନ ନିୟମ)
= a³ + 3a²b + 3ab² + b³
∴ (a + b)³ = (a + b) (a + b) (a + b)
(a – b)³ = (a – b) (a – b) (a – b) (ସଂଞା)
= {a(a – b) +(a – b)} (a – b) (ବଶ୍ନନ ନିୟମ)
= (a.a – a.b – b.a + b.b) (a – b) (ସଂଞା)
= (a² – ab – ba + b²) (a – b) (ସଂଞା)
= (a² – ab – ab + b²) (a – b) (ବଶ୍ନନ ନିୟମ)
= (a² – 2ab + b²) (a – b) (ସଂଞା)
= a(a² – 2ab + b²) – b(a² – 2ab + b²) (ବଶ୍ନନ)
= a.a² – a.2ab + a.b² – b.a² + b.2ab – b.b² (ବଶ୍ନନ)
= a³ – 2a²b + 2ab² – b³ + 2ab² – b³ (ସଂଞା)
= a³ – 2a²b + ab² – ba² + 2ab² – b³ (ବଶ୍ନନ ନିୟମ)
= a³ – 3a²b + 3ab² – b³ (ସଂଞା)
∴ (a – b)³ = (a – b) (a – b) (a – b)

(v) (a + b) (a² – ab + b²) = a³ + b³
ସମାଧାନ:
(a + b) (a² – ab + b²) = a(a² – ab + b²) + b(a² – ab + b²) (ବଶ୍ନନ)
= a.a² – a.ab + a.b² + b.a² – b.ab + b.b² (ବଶ୍ନନ)
= a³ – a²b + a.b² + b.a² – ab² + b³ (ସଂଞା)
= a³ – a²b + a.b² + a²b – ab² + b³ (କ୍ମମବିନିମୟୀ)
= a³ + b³

(vi) (a – b) (a² + ab + b²) = a³ – b³
ସମାଧାନ:
(a – b) (a² + ab + b²) = a(a² + ab + b²) – b( (a² + ab + b²) (ବଶ୍ନନ ନିୟମ)
= a.a² + a.ab + a.b² – b.a² – b.ab – b.b² (ବଶ୍ନନ)
= a³ + a²b + a.b² – b.a² – ab² – b³ (ସଂଞା)
= a³ + a²b + a.b² – a²b – ab² – b³ (କ୍ମମବିନିମୟୀ)
= a³ – b³

Question 27.
x ∈ R, x ≠ 0, a, b, c ∈ R ହେଲେ ପ୍ରମାଶି କର ଯେ \(\frac{1}{1+x^{b-a}+x^{c-a}}+\frac{1}{1+x^{c-b}+x^{a-b}}+\frac{1}{1+x^{a-c}+x^{b-c}}\) = 1
ସମାଧାନ:

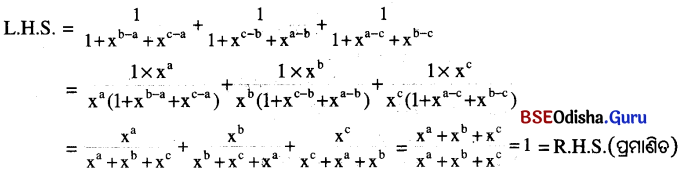
Question 28.
ନିମ୍ନଲିଖତ କ୍ଷେତ୍ରରେ x ର ମାନ ନିରୂପଣ କର :

(i) |x – 3| = 7
ସମାଧାନ:
|x – 3| = 7
ଯତି x – 3 ≥ 0 ⇒ |x – 3| = x – 3
∴ x – 3 = 7 ⇒ x = 3 + 7 = 10
ଯତି x – 3 ≤ 0 ⇒ |x – 3| = -(x – 3)
∴ -(x – 3) = 7 ⇒ -x + 3 = 7 ⇒ x = -7 + 3 ⇒ x = -4
∴ ନଣ୍ତେୟ ସମାଧାନ = {-4, 10}

(ii) |x + 1| = 11
ସମାଧାନ:
|x + 1| = 11 ଯତି x + 1 ≥ 0 ⇒ |x + 1| = x + 11
∴ x + 1 = 11 ⇒ x = 11 – 1 = 10
ଯତି x + 1 ≤ 0 ⇒ |x + 1| = -(x + 1)
∴ -(x + 1) = 11 ⇒ -x – 1 = 11 ⇒ -x = 11 + 1 = 12
⇒ x = -12
∴ ନଣ୍ତେୟ ସମାଧାନ = {10, -12}

(iii) |2x – 1| = 3
ସମାଧାନ:
|2x – 1| = 3 ଯତି 2x – 1 ≥ 0 ⇒ |2x – 1| = 2x – 1
∴ 2x – 1 = 3 ⇒ 2x = 3 + 1 = 4 ⇒ x = \(\frac{4}{2}\) = 2
ଯତି 2x – 1 ≤ 0 ⇒ |2x – 1| = -(2x – 1)
∴ -(2x – 1) = 3 ⇒ -2x + 1 = 3 ⇒ -2x = 3 – 1 = 2
⇒ x = \(\frac{2}{-2}\) = -1
∴ ନଣ୍ତେୟ ସମାଧାନ = {2, -1}

(iv) |3x + 4| = 5
ସମାଧାନ:
|3x + 4| = 5 ଯତି 3x + 4 ≥ 0 ⇒ |3x + 4| = 3x + 4
∴ 3x + 4 = 5 ⇒ 3x = 5 – 4 = 1 ⇒ x = \(\frac{1}{3}\)
ଯତି 3x + 4 ≤ 0 ⇒ |3x + 4| = -(3x + 4)
∴ -(3x + 4) = 5 ⇒ -3x – 4 = 5
⇒ -3x = 5 + 4 = 9 ⇒ x = \(\frac{9}{-3}\) = -3
∴ ନଣ୍ତେୟ ସମାଧାନ = {\(\frac{1}{3}\), -3}

Question 29.
ନିମ୍ନରେ ପ୍ରଦତ୍ତ ରାଶିମାନଙ୍କୁ ପରିମେୟ ଓ ଅପରିମେୟ ସଂଖ୍ୟାର ସମଷ୍ଟି ରୂପେ ପ୍ରକାଶ କର ।

(i) \(\frac{3}{3+\sqrt{5}}\)
ସମାଧାନ:
\(\frac{3}{3+\sqrt{5}}=\frac{3(3-\sqrt{5})}{(3+\sqrt{5})(3-\sqrt{5})}=\frac{9-3 \sqrt{5}}{3^2-(\sqrt{5})^2}=\frac{9-3 \sqrt{5}}{9-5}=\frac{9-3 \sqrt{5}}{4}=\frac{9}{4}-\frac{3 \sqrt{5}}{4}\)

(ii) \(\frac{\sqrt{2}}{1+\sqrt{8}}\)
ସମାଧାନ:

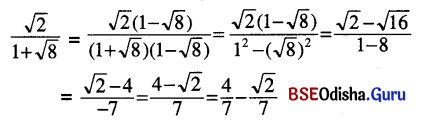
(iii) \(\frac{\sqrt{3}-1}{\sqrt{3}+1}\)
ସମାଧାନ:

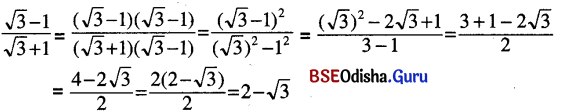
Question 30.
ନିମ୍ନଲିଖ୍ ଅସମୀକରଣମାନଙ୍କୁ ସମାଧାନ କର ।

(i) |x| = \(\frac{1}{2}\)
ସମାଧାନ:
|x| < \(\frac{1}{2}\) ⇒ –\(\frac{1}{2}\) < x < \(\frac{1}{2}\) (ସୂଢ୍ର ଅନୁସାରେ)
(a) ଯତି x ≥ 0 ହୁଏ ତେବେ |x| = x ∴ x < \(\frac{1}{2}\)
(b) ଯତି x < 0 ହୁଏ ତେବେ |x| = -x ∴ -x < \(\frac{1}{2}\) ⇒ x > –\(\frac{1}{2}\)
a ଓ bରୂ –\(\frac{1}{2}\) < x < \(\frac{1}{2}\)

(ii) |x| > 1
ସମାଧାନ:
|x| > 1
⇒ x < -1 କିମୃ‍। x > 1 (ସୂଢ୍ର ଅନୁସାରେ)
(a) ଯତି x ≥ 0 ହୁଏ ତେବେ |x| = x ∴ x > 1
(b) ଯତି x < 0 ହୁଏ ତେବେ |x| = -x ∴ -x > 1 ⇒ x < -1
a ଓ bରୂ ପାକବା x > 1 କିମୃ‍। x < -1

(iii) |3x| ≤ 5
ସମାଧାନ:
|3x| ≤ 5 ⇒ -5 ≤ 3x ≤ 5
⇒ \(\frac{-5}{3}\) ≤ \(\frac{3x}{3}\) ≤ \(\frac{5}{3}\) ⇒ \(\frac{-5}{3}\) ≤ a ≤ \(\frac{5}{3}\)

(iv) |2x| ≥ 3
ସମାଧାନ:
|2x| ≥ 3 ⇒ -3 ≥ 2x ≥ 3
⇒ 2x ≤ -3 କିମୃ‍। 2x ≥ 3 ⇒ \(\frac{2x}{2}\) ≤ -3 କିମୃ‍। 2x ≥ 3
⇒ x ≤ -3 ⇒ \(\frac{2x}{2}\) ≥ \(\frac{3}{2}\) ⇒ x ≥ \(\frac{3}{2}\) ∴ x ≤ -3 କିମୃ‍। x ≥ \(\frac{3}{2}\)

(v) |3x – 1| ≤ 7
ସମାଧାନ:
|3x – 1| ≤ 7 ⇒ -7 ≤ 3x – 1 ≤ 7
⇒ -7 + 1 ≤ 3x – 1 + 1 ≤ 7 + 1 ⇒ -6 ≤ 3x ≤ 8
⇒ \(\frac{-6}{3}\) ≤ \(\frac{3x}{3}\) ≤ \(\frac{8}{3}\) ⇒ -2 ≤ x ≤ \(\frac{8}{3}\)

(vi) |7x + 3| ≥ 5
ସମାଧାନ:
|7x + 3| ≥ 5
ସୂଢ୍ର ଅନୁସାରେ -5 ≥ 7x + 3 ≥ 5
⇒ 7x + 3 ≤ -5 କିମୃ‍। 7x + 3 ≥ 5
⇒ 7x + 3 – 3 ≤ -5 -3 ⇒ 7x + 3 – 3 ≥ 5 – 3
⇒ 7x ≤ -8 ⇒ 7x ≥ 2
⇒ \(\frac{7x}{7}\) ≤ \(\frac{-8}{7}\) ⇒ \(\frac{7x}{7}\) ≥ \(\frac{2}{7}\)
⇒ x ≤ \(\frac{-8}{7}\) ⇒ x ≥ \(\frac{2}{7}\)
∴ x ≤ \(\frac{-8}{7}\) କିମୃ‍। x ≥ \(\frac{2}{7}\)