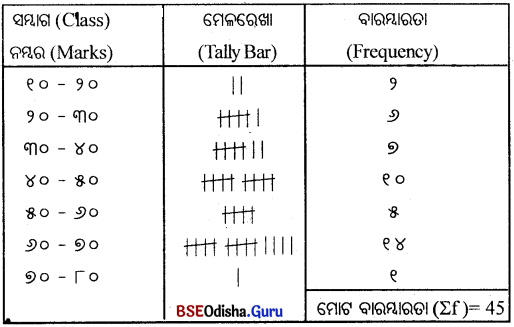
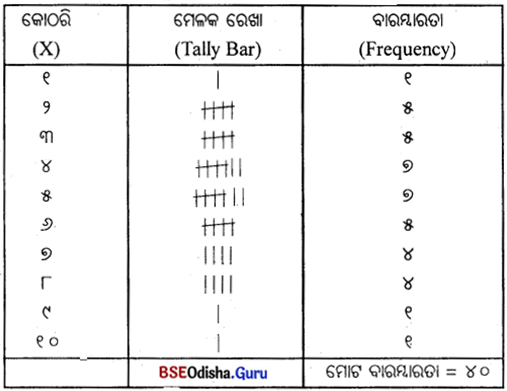
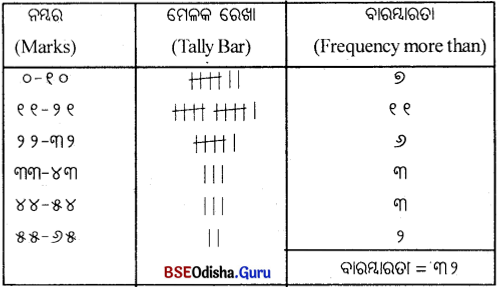
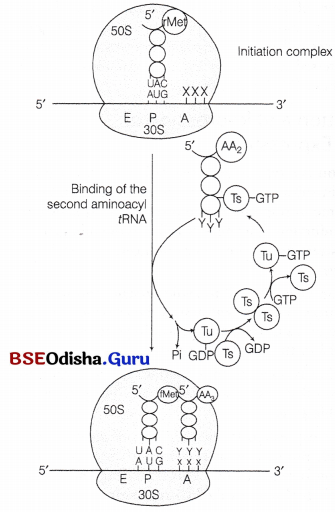
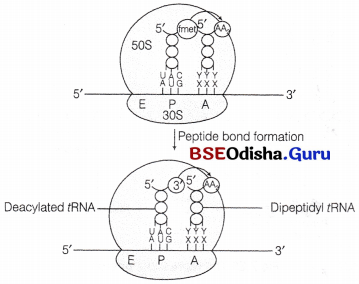
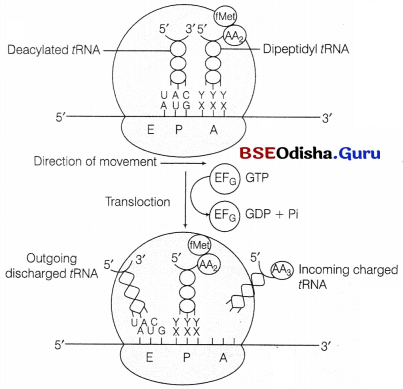
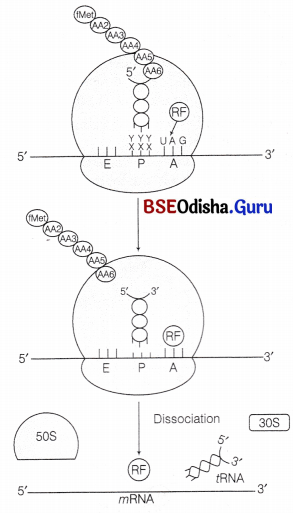
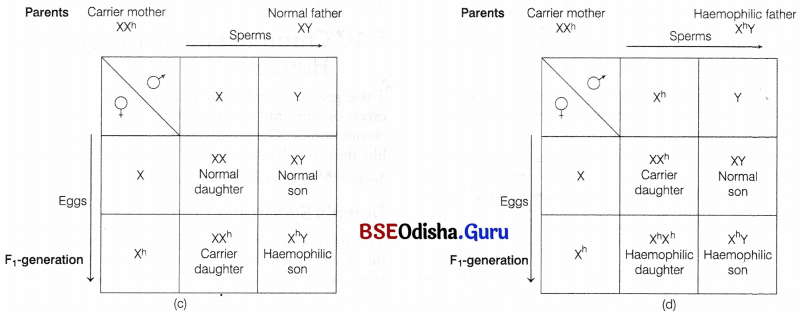
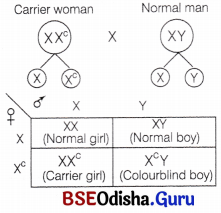
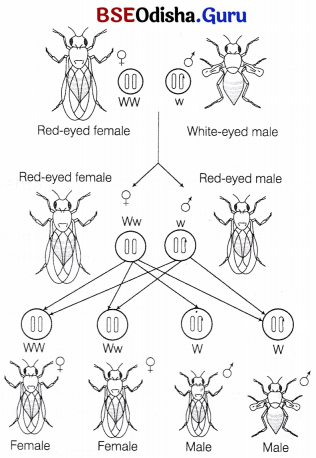
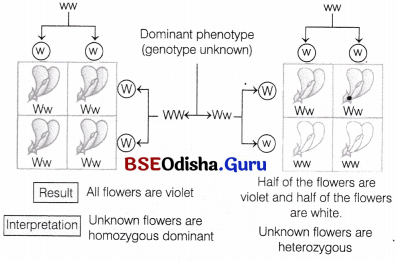
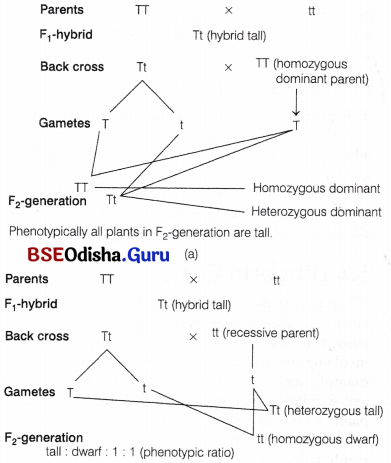
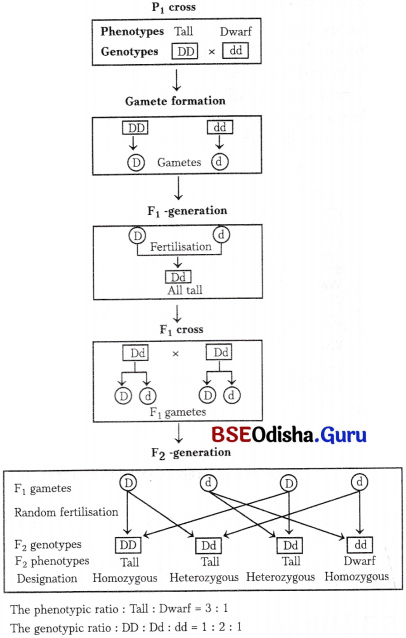
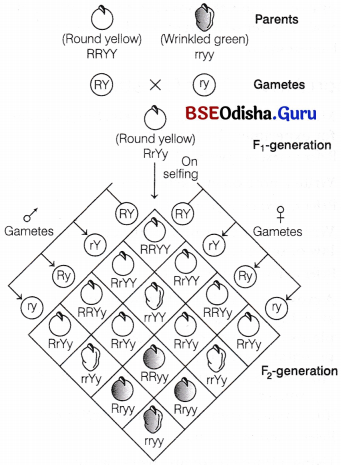
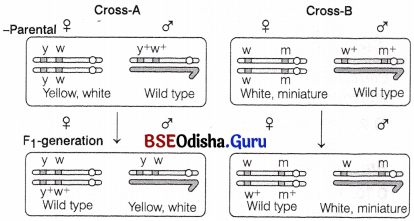
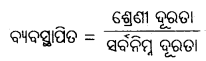Odisha State Board CHSE Odisha Class 12 Biology Solutions Chapter 8 Evolution Textbook Questions and Answers.
CHSE Odisha 12th Class Biology Chapter 8 Question Answer Evolution
Evolution Class 12 Questions and Answers CHSE Odisha
Very Short Answer Type Questions
Choose the correct options
Question 1.
Life originated on earth about
(a) 2.5 billion years ago
(b) 3.5 billion years ago
(c) 4.5 billion years ago
(d) 5.5 billion years ago
Answer:
(c) 4.5 billion years ago
Question 2.
Which theory proposes the formation of living beings from non-living things?
(a) Theory of panspermia
(b) Theory of abiogenesis
(c) Theory of biogenesis
(d) Theory of special creation
Answer:
(b) Theory of abiogenesis
Question 3.
Who proposed the chemical evolution of life?
(a) AI Oparin – JBS Haldane
(b) Louis Pasteur – AI Oparin
(c) Francesco Redi – JBS Haldane
(d) Spallanzani – Louis Pasteur
Answer:
(a) AI Oparin – JBS Haldane
Question 4.
Which of the following compounds Miller-Urey used in the experimental synthesis of amino acids?
(a) CH4 NH3,CO2 and H2O
(b) CH4,NH3,H2 and H2O
(c) CH4,CO2 H2 and H2O
(d) CH2,N2,H2 and H2O
Answer:
(b) CH4,NH3,H2 and H2O
![]()
Question 5.
Hot ocean water containing concentrated of prebiotic organic compounds was known as
(a) colloid
(b) crystalloid
(c) gelatinous mixture
(d) primordial soup
Answer:
(d) primordial soup
Question 6.
Which of the following was formed first?
(a) Virus
(b) Prokaryote
(c) Coacervates
(d) Eukaryote .
Answer:
(c) Coacervates
Question 7.
A paper on ‘natural selection’ and ‘origin of species’ was presented in the Linnaean Society of London in 1858 by
(a) Charles Darwin – Robert Malthus
(b) Charles Darwin – Alfred R Wallace
(c) Hugo de Vries – Robert Malthus
(d) Alfred R Wallace – August Weismann
Answer:
(b) Charles Darwin-Alfred R Wallace
Question 8.
Analogous organs have
(a) different origin and similar function
(b) similar origin and similar function
(c) similar origin and different function
(d) different origin and different- function
Answer:
(a) different origin and similar function
Question 9.
Find out the odd match.
(a) Aerial-Flying
(b) Fussorial-Burrowing
(c) Cursorial-Running
(d) Arboreal-Swimming
Answer:
(d) Arboreal-swimming
Question 10.
Which one of the following sets of organs constitutes vestigial organs?
(a) Appendix, coccyx and plica semilunaris
(b) Appendix, pectoral girdle and caecum
(c) Large intestine, coccyx and ear muscle
(d) Appendix, coccyx and rectum
Answer:
(a) Appendix, coccyx and plica semilunaris
Question 11.
What is the correct ascending order?
(a) Mesozoic, Cenozoic and Palaeozoic
(b) Cenozoic, Mesozoic and Palaeozoic
(c) Palaeozoic, Mesozoic and Cenozoic
(d) Palaeozoic, Cenozoic and Mesozoic
Answer:
(d) Palaeozoic, Cenozoic and Mesozoic
Question 12.
Who is known as the ’Father of Modern Palaeontology’?
(a) Leonardo da Vinci
(b) Karl Ernst von Baer
(c) Ernst Haeckel
(d) Georges Cuvier
Answer:
(d) Georges Cuvier
Question 13.
Find the incorrect match.
(a) Blood group ‘A’-Antigen A
(b) Blood group ‘AB’-No antibody
(c) Blood group ‘O’-Andgen A and B
(d) Blood group ‘B’-Antibody anti-A
Answer:
(c) Blood group-‘0’-antigen A and B
![]()
Question 14.
Which is not a case of chromosomal aberration?
(a) Recombination
(b) Duplication
(c) Inversion
(d) Translocation
Answer:
(a) Recombination
Question 15.
Which type of natural selection removes individuals from both ends of a phenotypic distribution?
(a) Directional
(b) Disruptive
(c) Stabilising
(d) None of these
Answer:
(c) Stabilising
Question 16.
Which is not a great ape?
(a) Gorilla
(b) Chimpanzee
(c) Orangutan
(d) Macaque
Answer:
(d) Macaque
Question 17.
What is the correct sequence in human evolution?
(a) Homo habilis, H. erectus, H. neanderthalensis, H. sapiens
(b) Homo erectus, H. habilis, H. neanderthalensis, H. sapiens
(c) Homo habilis, H. neanderthalensis, H. sapiens, H. erectus
(d) Homo erectus, H. neanderthalensis, H. habilis, H. sapiens
Answer:
(a) Homo habilis, H. erectus, H. neanderthalensis, H. sapiens
Fill in the blanks
Question 1.
Organic evolution refers to a change in diversity and ……….. in populations of organisms.
Answer:
adaptations
Question 2.
The concept of chemical evolution was proposed by JBS Haldane and a Russian scientist, ………… .
Ans
AI Oparin
Question 3.
Charles Robert Darwin hailed from …………….
Ans
Britain
Question 4.
Charles Robert Darwin went on a voyage on board the ship
Answer:
HMS Beagle
Question 5.
Jean Baptiste de Lamarck wrote a book, entitled ……….., which embodied his theory of inheritance of acquired characters.
Answer:
Philosophic Zoologique
Question 6.
Charles Darwin was inspired by the population theory proposed by …………… .
Answer:
Robert Malthus
Question 7.
Darwin’s contemporary ………… was studying population diversity in the erstwhile East Indies.
Answer:
Alfred Russel Wallace
Question 8.
The mutation theory was proposed by ………….. .
Answer:
Hugo de Vries
Question 9.
All the present day life has originated from a single ancestral form, designated as …………. .
Answer:
protobionts
Question 10.
A gene mutation involving only one nucleotide is called as …………….
Answer:
point mutation
![]()
Question 11.
Abiogenesis of simple organic molecules was experimentally proved by ………….. and …………..
Answer:
Miller, Urey
Question 12.
The ‘theory of inheritance of acquired characters was proposed by …………. who hailed from …………. .
Answer:
Lamarck, France
Question 13.
August Weismann’s ……….. theory gave a thunder blow to Lamarckism.
Answer:
germplasm
Question 14.
Charles Darwin studied the diversity of a class of birds, commonly known as ………….. in the Galapagos archipelago.
Answer:
Darwin’s finches
Question 15.
The original title of Darwin’s book was ……………. .
Answer:
‘On the origin of species by means of natural selection’.
Question 16.
Natural selection in action was demonstrated by …………. moth.
Answer:
peppered
Question 17.
The earliest form of horse was ………….. that was living in the plains of North America.
Answer:
Eohippus
Question 18.
The fossil of ……….. discovered from the sedimentary rocks of Bavaria, Germany is the missing link between reptiles and birds.
Answer:
Archaeopteryx
Question 19.
Digits II and IV persist in modern horse as reduced structures, known as ……….. bones.
Answer:
splint
Question 20.
Modifications of the basic pentadactyl limb plan in vertebrates to meet their needs is known as ……….
Answer:
homology
Question 21.
The arrangement of different eras, periods and epochs in their ascending order of time constitutes the …………..
Answer:
geological time scale
Question 22.
Peripatus is connecting link between …………. and …………….
Answer:
Annelida, Arthropoda
![]()
Question 23.
………… era is known as the era of reptiles.
Answer:
Mesozoic
Question 24.
Sudden reappearance of some ancestral characters in the present organisms is called as ……………
Answer:
atavism
Question 25.
The effect of …………. is larger in small populations and smaller in large populations.
Answer:
genetic drift
Answer each of the following in one word or more words, wherever necessary
Question 1.
The theory that explains that life originated on this planet from non-living chemical constituents.
Answer:
Theory of abiogenesis
Question 2.
The ocean water that contained concentrated amount of prebiotic organic compounds.
Answer:
Primordial soup or prebiotic
Question 3.
The droplets formed by the separation of high molecular weight organic compounds in a colloidal solution.
Answer:
Coacervates
Question 4.
Protenoids, when dissolved in water by boiling and then cooling, organised structures are formed.
Answer:
Microspheres
Question 5.
Buffon, Erasmus Darwin and Lamarck proposed theories on organic evolution, which had one thing in common.
Answer:
Inheritance of acquired characters
Question 6.
Name the naturalist, who proposed that ontogeny recapitulates phylogeny.
Answer:
Ernst Haeckel
Question 7.
Name the theory, which explains about the origin of amphibians from aquatic fish-like ancestors.
Answer:
Recapitulation theory
Question 8.
DNA → RNA → Protein concept.
Answer:
Central dogma
![]()
Question 9.
Genetic recombination occurs in cell division. Name the cell division.
Answer:
Meiosis
Question 10.
Hugo de Vries proposed mutation theory on his observations on the morphological features of a plant. Name the plant.
Answer:
Evening primrose (Oenothera lamarckiana)
Question 11.
Breakage, exchange and rejoining of homologous chromosomal segments.
Answer:
Genetic recombination
Question 12.
A single nucleotide substitution in the nucleotide sequence of a gene.
Answer:
Point mutation
Question 13.
The collection of all genes of a population of species.
Answer:
Gene pool
Question 14.
A sudden change in the genetic make up that ends up in a new expression.
Answer:
Mutation
Write whether the following statements are ‘True’or ‘False’
Question 1.
The primitive atmosphere was reducing.
Answer:
True
Question 2.
Heterotrophic organisms with aerobic respiration evolved prior to anaerobic ’ organisms.
Answer:
False
Question 3.
Continuous genetic variation originates through mutation.
Answer:
False
Question 4.
Serum proteins of closely related animals are similar in their amino acid sequences to a greater extent.
Answer:
True
Question 5.
Reptiles flourished in the Palaeozoic era.
Answer:
False
Question 6.
Close similarity in the nucleotide sequence between two organisms depicts close relationship between them. ‘
Answer:
True
Question 7.
Numerical changes, involving one or both chromosomes of a homologous pair, are known as euploidy.
Answer:
True
Question 8.
Genetic drift is the main driving force of evolution in a large randomly breeding population.
Answer:
True
Question 9.
Discontinuous variation is the product of mutation.
Answer:
True
![]()
Short Answer Type Questions
Question 1.
Explain the theory of spontaneous generation.
Answer:
Theory of spontaneous generation It states that life originated from non-living matter automatically. This theory is also known as theory of abiogenesis or autobiogenesis. It was also supported by von Helmont (1642), who claimed that the mice were formed in 21 days from a dirty, sweat-soaked shirt put in a wheat barn in the dark. Abiogenesis was continued to be believed till the 17th century.
Question 2.
What do you mean by chemical evolution?
Answer:
This theory was given by AI Oparin (1923) and JBS Haldane (1928). According to them, the first form of life came from pre-existing, non-living organic molecules (like RNA, protein, etc.) and chemical evolution was followed by the formation of life, i.e. formation of diverse organic molecules from inorganic constituents.
The conditions on the earth favouring chemical evolution were high temperature, volcanic storms and reducing atmosphere containing CH4, NH3, etc.
Question 3.
Describe Miller-Urey experiment.
Answer:
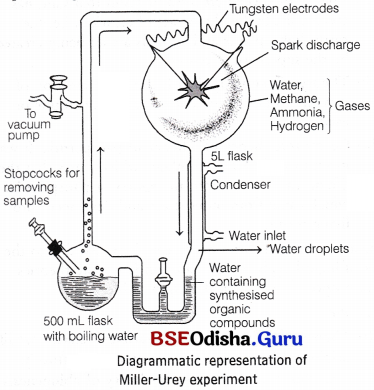
Stanley Miller and Harold Urey in 1953 performed an experiment to demonstrate that ultraviolet radiations or electrical discharges or a combination of these can produce complex organic compounds from a mixture of CH4, NH3, H2 and water vapour (H20) at 800° C.
Electric discharge was created in a closed glass flask containing CH4, NH3, H2 in the ratio of 2 : 1 : 2 as shown in figure. The conditions were set similar to those of the primitive atmosphere in the laboratory.
They observed the formation of amino acids while in similar experiments performed by other scientists the presence of complex molecules like sugar, pigments, nitrogen bases and fats in the flask were also observed. Further reactions occurred in the aqueous medium of flask resulted in the formation of complex organic molecules at the bottom of flask, such as polysaccharides, fats, proteins, nucleotides and later nucleic acids (DNA and RNA).
Hence, it was concluded that during the beginning of life on earth; complex organic compounds could have formed simpler inorganic precursors.
Question 4.
Explain prebiotic or primordial soup.
Answer:
Formation of molecular aggregates and cell-like structures Aggregates of complex organic molecules were formed in the oceans of the early earth which was termed the ‘Hot dilute soup or prebiotic or primordial soup’ by JBS Haldane (1920). These were considered as precursors of colloidal particles which could grow and divide. These are small complex molecules which are spherical and are covered by external mambranes.
Question 5.
What is prodigality of reproduction ? Give an example.
Answer:
Prodigality of Reproduction (Overproduction):
All organisms possess enormous fertility. They multiply in a geometric proportion with some organisms producing very large number of species. Despite of this high rate of reproduction of a species, its number remains constant under fairly stable environment. The production of more offsprings by some organisms and fewer by others is termed as differential reproduction.
![]()
Question 6.
Write three criticisms on Darwinism.
Answer:
Criticism to Darwinism
Darwin’s theory was widely accepted, but Sir Richard Owen and Adam Sedgewick criticised it due to following • reasons
(i) Darwin emphasised on inheritance of useful variations,. However, sometimes inheritance of small variations, which are not useful to individuals are also seen.
(ii) He could not explain the presence of vestigial organs and concept of use and disuse of organs.
(iii) Darwinism failed to explain the arrival of the fittest.
(iv) Darwinism failed to differentiate between the somatic and germinal variations and considered all types of variations as heritable.
Question 7.
Explain how homologous organs reflect organic evolution?
Answer:
Homologous Organs:
It is the relation among the organs of different groups of organisms, that show similarity in the basic structure and embryonic development, but have different functions. Homology in organs indicates common ancestry.
It is based on divergent evolution which leads to the formation of homologous organs.
Question 8.
Describe homology in early embryonic development.
Answer:
Homologous Organs and Homology:
It is the relation among the organs of different groups of organisms, that show similarity in the basic structure and embryonic development, but have different functions. Homology in organs indicates common ancestry.
It is based on divergent evolution which leads to the formation of homologous organs.
In divergent evolution, a same basic organ gets specialisation to perform different functions, in order to adapt to the different environmental conditions prevailing in the habitat, e.g. forelimbs of vertebrates. Examples of homology are as follows
- Structural organisation of vertebrate’s heart, brain, kidney, muscles, skull, etc.
- Different mouthparts of some insects.
- Forelimbs of animals like – whales, bats, cheetah and mammals (e.g. humans).
Question 9.
Explain the theory of recapitulation.
Answer:
Recapitulation in embryos Von Baer stated that during the embryo development, distantly related animals depart more and more than do closely animals. Ernst Haeckel (1905) reinterpreted Baer’s law in the form of recapitulation theory in the light of evolution. The theory of recapitulation or biogenetic law states that ontogeny (development of embryo) recapitulates phylogeny (ancestral sequence).
Question 10.
How do fossils support organic evolution?
Answer:
The study of fossil in different sedimentary layers indicates the geological period in which they existed. It also shows that the life forms varied over time and certain life forms are restricted to certain geological time scale. Hence, new forms of life have evolved at different times in the history of earth. All this is called palaeontological evidence.
Question 11.
Why do you call Archaeopteryx as a connecting link between reptiles and birds ?
Answer:
Archaeopteryx is a connecting link between reptiles and birds. It was of the size of crow and had both reptilian and avian characters. Presence of teeth in jaws, fingers having claws, long tail with free caudal vertebrae are the reptilian characters. While, presence of feathers on the body, and forelimbs modified into wings are the avian characters.
Question 12.
What do you mean by a geological time scale?
Answer:
Geological. Time Scale:
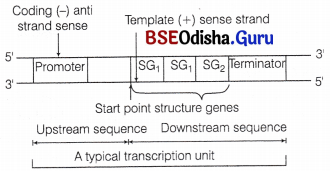
It covers the whole span of the earth’s history to correlate the evolutionary events in a proper sequence of ascending order of time. On the basis of time, the geological history of the earth has been divided into five eras namely, Archacozoic, Proterozojc, Palaeozoic, Mesozoic and Coenozoic.
Each era includes several periods and each period is further divided into epochs.
The most primitive era, i.e. Archaeozoic is placed at the bottom and the most recent era, i.e. Cenozoic is placed at the top.
Question 13.
Explain serological test.
Answer:
Serological tests These are tests done to study serum and other bodily fluids in animals. In serological tests, close similarity is found in species of a single genus, while genera of the same family show moderate reaction and families of the same order show slight, but detectable similarity. This indicates that closely related organisms show more similarity in protein structure and function.
![]()
Question 14.
What is industrial melanism?
Answer:
Industrial Melanism:
Industrial melanism in peppered moth (Biston betularia) in Manchester city is an example of natural selection. In England, 1850s before industrialisation there were more white-winged moths on trees than dark-winged or melanic forms. But after industrialisation, i.e. in 1920, dark-winged moths became more in number than white-winged moths. This is because during industrialisation, the tree trunks became dark due to air pollution (dust and soot particles).
Question 15.
Explain genetic drift.
Answer:
Random Genetic Drift:
Random genetic drift refers to a random change in gene frequency of a population. In small population, frequencies of particular alleles may change drastically by a single change alone. These changes usually occur randomly.
Sewall Wright recognised this phenomenon as genetic drift (also known as Sewall Wright effect.) In large population, this phenomenon is rare because only favourable variations are selected by nature and unfit variations are eliminated.
Thus, genetic drift acts as the driving force for evolution in large populations.
Question 16.
What is speciation ?
Answer:
Speciation:
It is the process of formation of one or more new species from an existing species due to the accumulation of inversible adaptive change in their structure. A species is a collection of a group of populations with common gene pool (i.e total collection of all genes and its allele in a population). The factors which influence speciation, include mutation, recombination, natural selection, hybridisation, genetic drift, polyploidy (i.e increase in number of chromosomal set) and isolation.
Question 17.
What is bottleneck effect ?
Answer:
Bottleneck Effect:
It occurs when there is a disaster of some sort that reduces the size of a large population to an insignificance. This leaves smaller variation among the small number of surviving individuals, which disables natural selection to operate. In this situation, random genetic drift becomes main driving force of evolution.
Question 18.
What is Hardy-Weinberg’s principle?
Answer:
Mutations introduce new genes into a species resulting in the change in gene frequencies. In 1908, GH Hardy and W Weinberg established a simple mathematical relationship to the study these gene frequencies and gave Hardy-Weinberg principle.
This principle states that the allele frequencies in a . population are stable and is constant from generation to generation, i.e. gene pool remains constant. This is .called genetic equilibrium or Hardy-Weinberg equilibrium.
Differentiate between the following
Question 1.
Abiogenesis and Biogenesis.
Answer:
Differences between abiogenesis and biogenesis are as follows
| Abiogenesis | Biogenesis |
| A theory which describes the origin of life on the earth from non-living thing is called Abiogenesis. | A theory which describes the origin of life on the earth from pre-existing living organisms is called Biogenesis. |
| It is based on observations and thoughts. | It was based on practical experiments and ffiaterial evidence. |
| It was supported by the fungus of bread and production of frogs in the mud. | It was supported by the experiments performed by Redi and Pasteur. |
| It gives no scientific reasoning about the production of life. | It describes the process of reproduction as an essential ability of living organism. |
![]()
Question 2.
Chemoautotrophs and Photoautotrophs
Answer:
Differences between chemoautotrophs and photoautotrophs are as follows
| Chemoautotrophs | Photoautotrophs |
| These are the organisms which obtain their energy by oxidising electron donor. | Phototrophs are the organisms that capture protons in order to acquire energy. |
| Energy source is the oxidizing energy of chemical compounds. | Energy source is mainly sunlight. |
| Classified as chemoorganotrophs and chemolithotrophs. | Classified as photoautotrophs and photoheterotrophs. |
| Examples include nitrifying bacteria like Nitrosomonas, sulfur bacteria like Thiothrix, etc. | Some examples are plants algae, cyanobacteria and phytoplanktons. |
Question 3. Chemical evolution and Biological evolution.
Answer:
Differences between chemical evolution and biological evolution are as follows
| Chemical evolution | Chemical evolution |
| It occurs due to changes in the structure of molecules from complex molecules to simple molecules with the passage of time. | It occurs due to changes in the structure of molecules from complex molecules to simple molecules with the passage of time. |
| It is relatively fast process and hence, it is possible to prove it in a laboratory. | It is relatively fast process and hence, it is possible to prove it in a laboratory. |
| It involves the evolution of chemical such as water vapour, methane, ammonia and hydrogen into organic molecules such as sugars which later combined to form big molecules such as proteins, RNA and DNA. | It involves the evolution of chemical such as water vapour, methane, ammonia and hydrogen into organic molecules such as sugars which later combined to form big molecules such as proteins, RNA and DNA. |
| Chemical evolution came into act before organic evolution. | Organic evolution is a consequence of biological evolution. |
Question 4.
Homologous organs and Analogous organs.
Answer:
Differences between homologous organs and analogous organs
| Homologous organs | Analogous organs |
| They have same basic structural plan. | They have totally different structural plan. |
| They are found in closely related organisms which arise from some common ancestor. | These organs found in totally unrelated organisms. |
| They differ in appearance. | They have similar appearance. |
| They are modified to carry out different functions. | These organs carry out the same function. |
| They lead to adaptive radiation or divergent evolution. | They lead to convergent evolution or adaptive convergence. |
Question 5.
Moulds and Casts.
Answer:
Differences between moulds and casts are as follows
| Moulds | Casts |
| A mold is a cavity left behind when the organic material is dissolved away. Only the external impressions remain during fossilisation. | A cast is usually a very finely preserved representation of the surface features of the organism during fossilisation. |
Question 6.
Genetic recombination and Mutation.
Answer:
Differences between genetic recombination and mutation are as follows
| Genetic recombination | Mutation |
| It is the production of offspring with combinations of traits that differ from those found in either parents. | It is random nucleotide alterations such as copying errors or changes induced by external mutagens. |
| It is performed by the cell during the preparation of gametes (sperm, egg, pollen) which are used for sexual reproduction. | It may take place both in somatic cells and germline cells. |
| Genetic recombination is heritable. | Mutation can be heritable as well as non-heritable. |
Question 7.
Somatic variation and Germinal variation.
Answer:
Differences between somatic variations and germinal variations are as follows
| Somatic variations | Germinal variations |
| Somatic variations are the variations in the somatic cells of an organism which may be acquired by them in their life. | Germinal variations are the variations in the germ cells of an organism. |
| These are not passed on to their progenies. | These are passed on to their progenies. |
Question 8.
Chromosomal aberration and Gene mutation.
Answer:
Differences between chromosomal aberration and gene mutation are as follows
| Chromosomal aberration | Gene mutation |
| Chromosomal aberration is any change in the number and structure of chromosomes in an organism. | Gene mutation is an alteration that occurs in the DNA base sequence of a gene. |
| It can change the total number of chromosomes in an organism. | Gene mutation does not cause changes in the total number of chromosomes in an organism. |
| It may include many gene alterations. | Gene mutation commonly refers to a single gene alteration. |
| Damages due to chromosomal aberration are large scale compared to gene mutation. | Nucleotide damage is small in scale compared to chromosomal aberration. However, it can cause serious health problems. |
Question 9.
Euploidy and Aneuploidy.
Answer:
Differences between euploidy and aneuploidy are as follows
| Euploidy | Aneuploidy |
| Euploidy is a variation in a chromosomal set of a cell or organism. | Aneuploidy is a variation in total chromosome number of a cell or organism. |
| The number of chromosome sets is changed. | The number of chromosome sets is not changed. |
| Cells have states of 3n, An, etc. | Ceils are in the states of 2n+1, 2n-1, n-1,n+1, etc. |
| Euploidy occurs due to fertilisation of one ovum with two sperms, etc. | Aneuploidy arises due to non-disjunction in meosis I and II and mitosis. |
| Euploidy is not seen in humans. | Aneuploidy is seen in humans. |
![]()
Question 10.
Natural selection and Genetic drift.
Answer:
Differences between natural selection and genetic drift are as follows
| Natural selection | Genetic drift |
| It is a process where more adaptive species are selected in response to the environmental challenges. | It is a random selection. |
| It occurs due to environmental challenges. | It does not occur due to environmental challenges. |
| It ends up with selecting the more successive trait over the detrimental trait. | Due to genetic drift important alleles may disappear completely. |
| It increases the frequency of the trait more adaptive to the environment. | Genetic drift rarely results in more adaptive species to the environment. |
| It increases genetic variation. | It does not increase genetic variation. Infact, sometimes it causes some variants to be extinct completely. |
Question 11.
Convergent evolution and Divergent evolution
Answer:
Differences between convergent evolution and divergent evolution are as follows
| Convergent evolution | Divergent evolution |
| It is supported by the analogous structures. | It is supported by the homologous structures. |
| It occurs in organisms which are not closely phylogenetically related. | It occurs in phylogenetically related organisms. |
| Example insects, birds, pterosaus and bats. All have developed the similar nature of the flight/wings. | Example Darwin’s finches. |
Long Answer Type Questions
Question 1.
Give an account of the chemical basis of origin of life.
Answer:
Life on earth appeared 500 million years after its formation. In order to explain origin of life on the earth, different theories were given by different thinkers and scientists. They are
1. Theory of special creation It states that God has created life by his divine act of creation, i.e. the earth, light, plants and animals are all being created by the supernatural power.
2. Theory of catastrophism It states the creation of new life forms occurred after each catastrophe on earth.
3. Cosmozoic theory or Theory of panspermia It was given by early Greek thinkers, which states that the life on earth arose from the spores or panspermia, which came from outer space and developed into living forms.
The above three theories have been discarded due to the lack of logical explanation. Later on few more theories were proposed to explain the orgin of life.
These are
(i) Theory of spontaneous generation It states that life originated from non-living matter automatically. This theory is also known as theory of abiogenesis or autobiogenesis. It was also supported by von Helmont (1642), who claimed that the mice were formed in 21 days from a dirty, sweat-soaked shirt put in a wheat barn in the dark. Abiogenesis was continued to be believed till the 17th century.
(ii) Theory of biogenesis According to this theory, life originates from pre-existing life. This theory was supported by some scientists like Francisco Reddi (1668), Lazzaro Spallanzani (1767), Louis Pasteur (1862), Harvey and Huxley.
Chemical Evolution:
This theory was given by AI Oparin (1923) and JBS Haldane (1928). According to them, the first form of life came from pre-existing, non-living organic molecules (like RNA, protein, etc.) and chemical evolution was followed by the formation of life, i.e. formation of diverse organic molecules from inorganic constituents.
The conditions on the earth favouring chemical evolution were high temperature, volcanic storms and reducing atmosphere containing CH4, NH3, etc.
Chemical Evolution has Occurred in Following Steps
(i) Primitive earth had no atmosphere and it was anaerobic. Initially, the earth was a ball of hot gaseous mass.
(ii) Formation of Early Molecules
(a) Earth gradually began to cool and condense into a solid form. As a result, the free atoms or elements present on earth began to segregate into three concentric masses according to their weight.
(b) The heavier elements like nickel, iron, etc., moved to the core of the earth, intermediate one like silicon and aluminium moved to the middle and the lighter elements like oxygen, nitrogen, hydrogen, carbon, etc., remained on the surface and formed the early atmosphere of earth.
(c) With further cooling of the earth lighter elements such as water (H2O), methane (CH4), ammonia (NH3), hydrogen cyanide (HCN) . and oxides of carbon were formed. The primary atmosphare was devoid of free molecular oxygen (O2) due to which it was of reducing type.
Hot oceans, seas, lakes and other water bodies were formed due to the accumulation of heavy rainwater in the depressions of the earth.
(iii) Formation of simple organic molecules The high concentration of simple inorganic compounds (CH4,HCN,NH3) in water bodies induces them to react with each other so as to produce some unsaturated hydrocarbons.
As a result of further interaction of these hydrocarbons, some simple organic compounds such as simple sugars (e.g. glucose, ribose, deoxyribose, etc.), nitrogenous bases (purines like adenine, guanine and pyrimidines like thymine, cytosine and uracil), amino acids, fatty acids and glycerols were formed.
The energy required for these reactions came from the following sources
- Solar radiations like ultraviolet light (UV) rays, cosmic rays and X-rays, etc.
- Electrical discharge from lightning. High energy radiations from radioactive unstable isotopes on primitive earth.
(iv) Formation of complex organic molecules A number of hydrocarbons, purines and pyrimidine bases, amino acids, fatty acids, sugars and other organic compounds were accumulated in the primitive seas. Further reactions like polymerisation lead to the formation of larger organic molecules which later on formed complex organic molecules like polysaccharides, fats, proteins, nucleotides and then nucleic acids (DNA and RNA).
(v) Formation of molecular aggregates and cell-like structures Aggregates of complex organic molecules were formed in the oceans of the early earth which was termed the ‘Hot dilute soup or prebiotic or primordial soup’ by JBS Haldane (1920). These were considered as precursors of colloidal particles which could grow and divide. These are small complex molecules which are spherical and are covered by external mambranes.
These colloidal aggregrates were called coacervates by Oparin and microspheres by Sydney Fox (1965).
The firest non-cellular cells were believed to contain nucleoproteins and other macromolecules like polypeptides, lipids, etc. These cells were called protocells or protobionts or eubionts and they in the ancient ocean represented the beginning of life approx. 3.5 billion years ago. Probably viruses were evolved at the same time.
The first cellular life forms are believed to be evolved approximately 2 billion years back by the aggregation of various non-living molecules. From there, the evolution of diverse species of organisms occurred in course of time.
![]()
Question 2.
Discuss the evidences of organic evolution from comparative anatomy and morphology.
Answer:
Evidences from Comparative Anatomy and Morphology
These evidences help to identify the similarities and differences among the organisms of today and those that existed years ago. Comparative study of external and internal structure can be used to understand the occurrence of organic evolution.
These can be determined by the following types
Homologous Organs and Homology
It is the relation among the organs of different groups of organisms, that show similarity in the basic structure and
embryonic development, but have different functions. Homology in organs indicates common ancestry.
It is based on divergent evolution which leads to the formation of homologous organs.
In divergent evolution, a same basic organ gets specialisation to perform different functions, in order to ‘ adapt to the different environmental conditions prevailing in the habitat, e.g. forelimbs of vertebrates. Examples of homology are as follows
- Structural organisation of vertebrate’s heart, brain, kidney, muscles, skull, etc.
- Different mouthparts of some insects.
- Forelimbs of animals like – whales, bats, cheetah and mammals (e.g. humans).

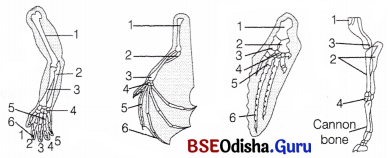
Flomologous organs as exhibited by the forelimbs of vertebrates; (a) Fluman, (b) Bat, (c) Whale, (d) Horse
Adaptive Radiation (Divergent Evolution):
It is the diversification of the organisms of a population into a number of new groups with adaptive characters suiting their need for survival.
Thus, it can be concluded that adaptive radiation and divergent evolution are interrelated and based on the modification of homologous structures. This can be proved studying the basic pattern of the pentadactyl limb which has undergone adaptive modifications in vertebrates,
All these animals have five digits (pentadactyl) in their forelimbs. All these digits possess the same number of skeletal elements that are arranged in same order (i.e. proximal to distal) along with similar muscle, nerve fibres, blood vessels, etc. These limbs have undergone adaptive modifications so as to perform the required funtions to adapt to their environment.
Similar adaptive modification rule also applies to mammals. In figure, a typical pentadactyl limb is seen in a terrestrial mammal.
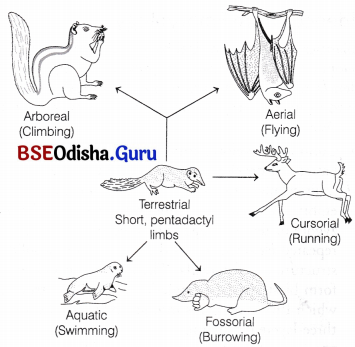
Adaptive radiation in the limb structure of mammals
This pattern has been modified for different functions like running (cursorial), swimming (aquatic), flying (aerial), climbing (arboreal) and burrowing (fussorial). Thus, all mammals have originated from an ancestral terestrial mammal through adaptive modifications of the basic pentadactyl limb plan.
Analogous Organs and Analogy:
In contrast to homologous organs, the analogous organs are different in their basic structure and developmental origin, but appear same and perform similar functions.
This relationship between the structures of different groups of animals due to their similar functions is called analogy or convergent evolution.
Examples of analogy are as follows
1. Wings of an insect a bird, Pterosaur (extinct flying reptile and a bat (flying mammal) show analogy. The wings are modified forelimbs that are adapted for flight.
The internal organisation of vertebrate (reptile, bird and bat) wings is same and they are composed of muscles and bones whereas, the wings of insect do not possess bones and muscles. They are only thin membranous extentions of exoskeleton and are made up of chitin.
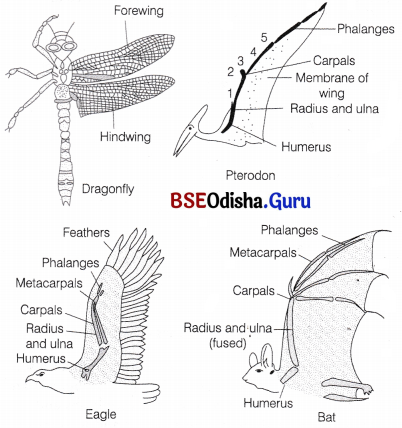
2. Flippers of dolphin and penguin.
3. Fins of fishes and flippers of whales.
4. Tracheae of an insect and lungs of the vertebrates are adapted for respiration, but are not homologous, as tracheae are ectodermal in origin, whereas the lungs are endodermal in origin.
Adaptive Convergence (Convergent Evolution):
In adaptive convergence, separate lineages show similar morphology under the influence of similar environmental factors. The existence of analogous structures also suggest the occurrence of convergent evolution. It may be explained in terms of the environment acting through the agency of natural selection and favouring those variations which confer increased survival and reproductive potential of the organisms possessing them.
Marsupial mammals in Australia are a good example to study adaptive convergence or convergent evolution.
Vestigial Organs:
The degenerated, rudimentary organs which are non-functional in the possessor, but were functional in their ancestor and in related animals are called vestigial organs. There are more than 90 vestigial organs in the human body. Some examples in human are coccyx (tailbone), nictitating membrane ( semilunar fold or plica semilunaries or 3rd eyelid), caecum, vermiform appendix, canines, wisdom teeth, tonsils, body hair, auricular muscles, mammary glands in males, etc.
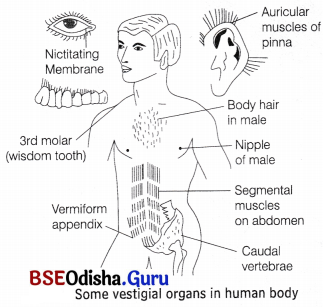
Vestigial organs are present in some other animals also, e.g. splint bones representing metacarpals of digits II and IV in horse, small bones representing hindlimbs and pelvic girdle in python and boas, wings and feathers in flightless bird kiwi of New Zealand, etc.
In plants, Dandelions and some other asexually reproducing plants retains flower which produce pollen grains necessary for sexual reproduction.
Atavism or Reversion:
It is the sudden reappearance or refunctioning of some ancestral organs, which have either completely disappeared or are present as vestigial organs.
It supports the idea of organic evolution, that living organisms have the ability to develop even lost or non-functional structures. For example, long and dense body hair, ability to move pinna in .some individuals, birth of a human baby with a small tail, presence of additional mammae in some individuals, elongated canine teeth, etc.
![]()
Question 3.
Give an account of the embryological evidences of organic evolution.
Answer:
Evidences from Embryology:
Similarities and degree of intimacy in the embryonic development of various animals provide the supportive evidences of organic evolution. Some conclusions are derived from the study of comparative embryology, which are as follows
1. Common developmental pattern A common pattern of development is found in all the multicellular organisms. The development of embryo by sexual reproduction starts from diploid zygote or fertilised egg. The zygote undergoes repeated cleavage or cell division to form a solid structure called morula. The morula divides to form blastula, i.e. a single-layered hollow structure, which finally develops into gastrula, i.e. two to three-layered structure.
The animals with two-layered gastrula are termed as diploblastic, e.g. in coelenterates. The animals in which three-layered gastrula is found are known as triploblastic, e.g. frog, lizard, etc. These two or three layers of gastrula are termed as primary germ layers, which give rise to the entire animal. Thus, the similar early embryonic development shows close relationship among all the multicellular organisms.
2. Similarity in early embryos of vertebrates If a comparative study of embryos of vertebrates at same age is done, it is observed that they resemble one another. Such similarities suggest that these animals have common ancestry.
Some similarities in early embryonic stages are as follows
Presence of gill clefts, notochord, tail, rudimentary eyes and ears, etc. in all vertebrates from fishes to mammals.
Notochord is replaced by vertebral column in all adult vertebrates.
Gills are replaced by lungs in adult amphibians, reptiles and mammals.
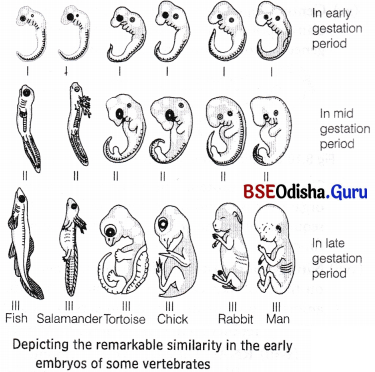
3.Recapitulation in embryos Von Baer stated that during the embryo development, distantly related animals depart more and more than do closely animals. Ernst Haeckel (1905) reinterpreted Baer’s law in the form of recapitulation theory in the light of evolution. The theory of recapitulation or biogenetic law states that ontogeny (development of embryo) recapitulates phylogeny (ancestral sequence).
This means that the life history of an animal reflects its evolutionary history. For example, during the life history, frog’s tadpole larva resembles fishes in habits and structure. It suggests that amphibians have evolved from fish ancestors.
Embryo logical Evidences in Plants
These include
- Presence of filamentous green algae-like structure, i. e. protonema during development of Funaria (moss).
- Pteridophytes and primitive -gymnosperms like Cycas and Ginkgo have flagellated sperms and they depend on water for fertilisation. It strengthens the fact that gymnosperms have evolved from pteridophytes.
Question 4.
Describe palaeontological evidences of organic evolution.
Answer:
Evidences from Palaeontology:
Palaeontology is the study of fossils of plants and animals that lived in prehistoric times. Leonardo da Vinci (1452-1519), an Italian painter is known as the ‘Father of Palaeontology’ and Baron Georges Cuvier (1769-1832) is known as ‘The Founder of Modern Palaeontology’.
The study of fossil in different sedimentary layers indicates the geological period in which they existed. It also shows that the life forms varied over time and certain life forms are restricted to certain geological time scale. Hence, new forms of life have evolved at different times in the history of earth. All this is called palaeontological evidence.
Fossils:
These are the material remains (bones, teeth, shells) or traces (physical or chemical) of ancient organisms induding plants and animals. According to Charles Lyell, fossil is any body or traces of body of animal or plant buried and preserved by the natural causes. .
Fossilisation is the process of formation of fossils. Fossils are generally preserved in sedimentary rocks in which multiple layers are present and the lowermost layer gets harden into rock under pressure. These are formed when parts of dead organisms decay with the passage of time and get replaced by inorganic materials. The hard parts of the body (i.e. bone, teeth, shell, etc.), are preserved more readily than soft parts, into rocks. Both animals as well as plants can be fossilised as additional layers get deposited with time.
Fossils are also formed by processes other than petrification, e.g. an organism may get buried intact in ‘ preservatives like resins, snow, oil, tar, volcanic, ash, etc.
Sometimes, the organism or its parts get washed away to water bodies and settle down at the bottom. Gradually they get covered by the layers of mud and sand. Particularly when buried in rapidly hardening mud, they decay completely and the space it occupies, becomes filled with another kind of material forming moulds and casts.
Types of Fossils:
Some general types of fossils are given below
(i) Unaltered It includes animals, plants and humans who got embedded in permafrost of arctic/alpine snow and remain preserved in actual state, e.g. wooly mammoth (25000 years old in Siberia) and insects trapped in the amber of plants.
(ii) Petrifications The fossils in which hard body parts (organic matter) get replaced by mineral matter like silica, pyrites and calcium, etc. In some petrified fossils, even cellular details are found. This process is used to preserve original structures of organisms.
(iii) Moulds They are hardened encasements formed in the outer parts of extinct organic remains which later decayed leaving cavities.
(iv) Casts They are hardened pieces of mineral matter deposited in the cavities of moulds.
(v) Impressions/Imprints They are external features of organisms or their parts that are left due to hardening rocky matter before they completely decay.

(a) Imprint of a crustacean, (b) Mould of a bivale, (c) Insect trapped in amber, (d) Petrified softwood, (e) Petrified cone of Araucaria mirabilis (a coniferous tree)
Important Characteristics of Fossils:
The fossil records are direct evidences that support organic evolution due to the following reasons
1. Fossils of different ages are mostly found in the different layers of sedimentary rocks in an ascending order, i.e. from simple to complex forms.
2. The lower layers of rocks of early era contain fossils of simple nature. In upper layers more recent fossils, which are more recent and complex in structure. Fossils are not found in the rocks of the Archaeozoic (first) Era.
3. In the rocks of the second era, i.e. Proterozoic, only few fossils are found. These are simple, soft-bodied organisms, such as marine invertebrates. In the upper strata of rocks, fossils are more in number, belonging to organisms of later ages.
4. The fossils of two consecutive strata are different from each other indicating the occurrence of progressive changes in course of time.
5. Certain mammals, such as horse, elephant, camel and man, have complete fossil records. They clearly explain the gradual evolution of these species.
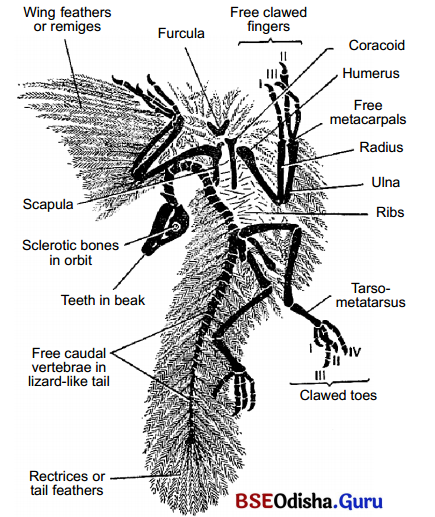
6. Fossils of some transitional forms (also called connecting links or missing links) explain the emergence of a new species from its ancestor. For example, fossil of Archaeopteryx discovered from the rocks of Jurassic Period at Bavaria, Germany in 1861 is a connecting link between birds and reptiles. As a transitional form, it possessed the characters of both reptiles and birds.
7. Living fossils are the living organisms which are similar in appearance to a recorded fossil of distant ancestors but they usually have no close relatives. Such organisms have undergone very slow changes over a long span of time, e.g Latimeria (a coelacanth fish).
8. The approximate ages of fossils can be determined by different radioactive dating methods.
9. Extinction of species can be explained by the fossil records of that species, e.g. dinosaurs extinct about 66 million years ago.
![]()
Question 5.
Describe Darwin’s theory of natural selection and origin of species and discuss about the criticisms.
Answer:
Darwinism (Natural Selection Theory):
Charles Robert Darwin was born in 1809. In 1831, he accepted an unpaid post of naturalist on the survey ship, called HMS Beagle. In his voyage, he spent five years in sea charting the East Coast of South America. During a five week stay on the Galapagos Archipelago Islands, he was struck by the similarities shown by the flora and fauna of the islands and mainland. In particular, he was intrigued by the characteristic distribution of species of tortoises and finches.
Darwin observed different types of beaks in the same population of finches. He termed this phenomenon as adaptive radiation which explains that the changes in beak structure were the result of adaptations to the available food to the native finches. Over the years, the ancestral beak evolved into diverse types of beaks. Thus, Darwin realised the importance of competition and adaptation in the evolution of finches.
After his return, Darwin formulated his concept of organic evolution. He was also influenced by a paper published by Robert Malthus (1838) on populations, which states that the population increases in a geometric progression, while the food supply increases more slowly. Therefore, the food supply becomes a limiting factor. In the meantime, another naturalist Alfred Russel Wallace, came to the same conclusions as Darwin regarding natural selection. The content of Wallace’s write-up was similar to Darwin’s thinking.
Darwin and Wallace presented papers on their ideas which were published in the ‘Journal of the Proceedings of The Linnaean Society of London in 1858. Darwin published a book entitled ‘On the Origin of Species by Means of Natural Selection (later changed to ‘Origin of Species’ In its 6th edition in 1872), embodying his observations and conclusions in 1859.
Postulates of Darwinism:
The main postulates, which formed the basis of Darwin’s theory of natural selection are as follows
(i) Prodigality of Reproduction (Overproduction):
All organisms possess enormous fertility. They multiply in a geometric proportion with some organisms producing very large number of species. Despite of this high rate of reproduction of a species, its number remains constant under fairly stable environment. The production of more offsprings by some organisms and fewer by others is termed as differential reproduction.
(ii) Limiting Factors
The resources like food, space, etc., remain limited inspite of rapid multiplication of the individuals of all the species. It helps to check the increased number of animals and plants.
(iii) Struggle for Existence
The limited amount of resources and overproduction of organisms are the main causes of struggle for existence. Various types of struggle help an organism to cope up with unfavourable environmental conditions.
The three types of struggles are as follows
(a) Intraspecific struggle It is the struggle among the individuals of same species for their common requirements like food, shelter, mate, breeding places, etc.
(b) Interspecific struggle It is the struggle between the individuals of different species for their similar requirements like food and space.
(c) Environmental struggle It is the struggle of living forms against the environmental conditions like extreme heat, cold, drought, earthquakes, storms, disease, volcanic eruption, etc.
(iv) Variations and Heredity
All individuals are dissimilar in some of their characters except the identical twins. This dissimilarities are mainly due to the variations. These are the small or large differences among the individuals. Variations allow some individuals to better adjust with their environment.
Variations can be categorised into the following types
1. Somatic variations These variations affect the somatic cells of an organism. They are also called modifications or acquired characters because they are aquired by an individual during its lifetime. These are caused by various environmental factors, use and disuse of organs and conscious efforts, etc.
2. Germinal variations These are inheritable variations recognised by Darwin but he had no idea of inheritance of characters. They are formed mostly in germinal cells. They are further of two types
• Continuous (gradual) variations These are fluctuating variations, which oscillate due to race, variety and species.
• Discontinuous (sudden) variations These appear suddenly and show no ‘spots’ gradation. These variations were termed as ‘spots’ by Darwin and ‘mutation’ by Hugo de Vries. Darwin regarded continuous variations to be more important because the discontinuous variations being mostly harmful would not be selected again.
(v) Survival of the Fittest and Natural Selection:
The organisms, which have inherited favourable variations generally survive. This is termed as ‘survival of the fittest’ (the phrase being originally used by Herbert Spencer). Whereas, the organisms without such variations appear unfit and get eliminated. Nature plays a decisive role in selecting the fit organisms.
Natural selection is based on merit and is without any prejudice or bias. It eliminates the unfit ones and selects those organisms that are most fit to survive in a particular environment and to produce offsprings. Survival alone does not make any sense from evolution point of view.
The fit organisms must reproduce to contribute to the next generation. Lerner (1959) says, ‘Individuals having more offsprings are the fit ones’.
(vi) Origin of New Species (Speciation):
Darwin considered that as a result of struggle for existence, variability (continuous variations) and inheritance, species became better adapted to their environment. These beneficial adaptations are preserved and accumulated in the individuals of species generation after generation. This results into the origin of new species or speciation and the resultant offsprings become visibly distinct from their ancestors.
Criticism to Darwinism:
Darwin’s theory was widely accepted, but Sir Richard Owen and Adam Sedgewick criticised it due to following reasons
(i) Darwin emphasised on inheritance of useful variations,. However, sometimes inheritance of small variations, which are not useful to individuals are also seen.
(ii) He could not explain the presence of vestigial organs and concept of use and disuse of organs.
(iii) Darwinism failed to explain the arrival of the fittest.
(iv) Darwinism failed to differentiate between the somatic and germinal variations and considered all types of variations as heritable.
(v) Darwin’s natural selection theory was based on the mistaken concept of artificial selection. He wrongly believed that changes brought on by domestication of animal were also heritable.
(vi) Darwin failed to recognise the large fluctuating variations (occurring due to mutation). He only believed in the occurrence of small continuous variations.
Darwin proposed ‘theory of pangenesis’ explaining that pangenes or gemmules are transmitted from one generation to next. However, this theory was refuted by Weismann’s germplasm theory.
Question 6.
Discuss about the synthetic theory of organic evolution.
Answer:
Modern Synthetic Theory of Organic Evolution:
The fundamental mechanisim of evolution as explained by Darwin and his contemporaries underwent major modification with the progress in genetics.
Mendel’s laws of inheritance were applied to various theories (like natural selection). The validity of these laws were later verified by Correns, Tschermark and de Vries. It came to light that mutation and genetic recombination were the cause of genetic variation in living organisms.
These variations were used as the raw material on which natural selection acted on, leading to evolution of new species. The process of evolution as a population character not an individual one was later on proposed by GH Hardy and W Weinberg. According to them, a disturbance in the gene pool of a population results in evolution. Among these new developments, the concept of modern synthetic theory (post-Darwinian synthesis) was proposed.
The modern synthetic theory is based on the work of a number of scientist namely-Dobzhansky’s (1937) Julian Huxley (1942), Ernst Mayr (1970), RA Fisher (1958), JBS Haldane, Sewall Wright (1968) and GL Stebbins (1971). Stebbins in his book ‘Process of Organic Evolution discussed the modern synthetic theory.
This theory is a collective explanation of the fundamental mechanism of evolution. Homologous recombination, mutation, natural selection, isolation, genetic drift and migration form the basis of the mechanism of evolution.
Genetic Recombination:
These are the homologous combinations between genes present on different chromosomes (i.e. paternal and maternal) during gametogenesis. It can occur by following ways
(i) Crossing over Mutual exchange of genes between non-sister chromatids of homologus chromosomes during meiosis-I. It forms multiple variations in a population.
(ii) Independent assortment of chromosomes It forms genetically different haploid gametes during meiosis which bring about variations in new generation.
(iii) Random fusion of gametes During sexual reproduction, random fusion of male and female gametes produces a new individual.
Changes in Chromosome Number and Structure:
Chromosomal mutations or aberrrations arise due to change in number and structure of chromosomes. Chromosomal number may change in followinng two ways
(i) Polyploidy (increase in number of chromosome sets)
(ii) Aneuploidy (change in number of one or both chromosomes of a homologous pair). When the change occurs in the chromosomal morphology, it is called chromosomal aberration.
These are of four types
(i) Deletion Loss of a segment of a chromosome.
(ii) Duplication Doubling of a chromosomal segment.
(iii) Inversion Reversal in the order of genes.
(iv) Translocation Mutual exchange of a segment of chromosome between two non-homologous chromosomes.
Gene Mutations:
In 1901, Hugo de Vries carried out experiments on evening primrose plant (Oenothera lamarckiana) and proposed the mutation theory of evolution. This theory states that the evolution occurs by the sudden large differences or mutations in the population. Mutation is the sudden change in appearance or variations in an individual or a population. When mutation affects only a single nucleotide, it is called point mutation.
However, when more than one nucleotide is involved in mutation, it is called gross mutation. These mutations results in drastic changes which can be lethal or insignificant or useful. They lead to the new phenotypes. Though mutations are random and occur at very slow rates, they are sufficient to create considerable genetic variations for speciation to occur.
Natural Selection:
It is the most widely accepted theory for explaining the mechanism of evolution, profounded by Charles Darwin and Alfred Russel Wallace. Natural selection selects the favourable variation and allows such organisms to reproduce. Meanwhile, harmful or non-adaptive variations are discouraged by natural selection and such organisms are eliminated from the population. Therefore, variations act as raw material natural selection which decides the favourable traits to continue through generations.
Isolation:
The mechanism by which a population gets segregated into two or more subtypes by a geographical barrier, such that each subtype influences a different environment, is called isolation.
This segregation can occur due to
(i) Geographical isolation When two related populations occupy geographically or spatially separated areas.
Such species are called as allopatric species. These species become so different to each other that when they are brought together, they fail to reproduce.
(ii) Reproductive isolation The prevention of interbreeding between the population of two different species. Such reproductively isolated species are called as sympatric species.