BSE Odisha 10th Class Maths Solutions Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 6(b)

Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 6(b) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 6(b)

Question 1.
ବନ୍ଧନୀ ମଧ୍ଯରୁ ସଠିକ୍ ଉତ୍ତରଟି ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଯଦି (1, – 2) ବିନ୍ଦୁଟି (4, 2) ଓ (K, – 6) ବିନ୍ଦୁଦ୍ବୟର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ହୁଏ, ତେବେ k = ………. । [-2, 2, – 4, 4]
(ii) (- 2, 3) ଓ (3, – 2) ବିନ୍ଦୁଦ୍ଵୟର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ହେଉଛି ………. । [(1, 1), (\(\frac{1}{2}, \frac{1}{2}\)), (\(\frac{5}{2}, \frac{5}{2}\)) (\(-\frac{1}{2}, -\frac{1}{2}\))]
(iii) ଏକ ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁ ହେଉଛି ମୂଳବିନ୍ଦୁ; ଯଦି ରେଖାଖଣ୍ଡଟିର ଏକ ପ୍ରାନ୍ତବିନ୍ଦୁ (2, 3) ହୁଏ, ତେବେ ………. । [(-2, 3), (2,-3),(-2,-3) (\(\frac{1}{2}, \frac{3}{2}\))]
(iv) (0, 2) ଓ (2, 0) ବିନ୍ଦୁଦ୍ଵୟର ରେଖାଖଣ୍ଡକୁ 1 : 2 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥ‌ିବା ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ………. । [(\(\frac{4}{3}, \frac{2}{3}\)), (\(\frac{4}{3}, \frac{2}{3}\)), (-2, 4),(4, -2)]
ଉତ୍ତର:
(i) -2
(ii) (\(\frac{1}{2}, \frac{1}{2}\))
(iii) (-2, -3)
(iv) (\(\frac{2}{3}, \frac{4}{3}\))

Question 2.
ନିମ୍ନଲିଖ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଦତ୍ତ ବିନ୍ଦୁମାନଙ୍କୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କର ।
(i) (3, 4), (1,-2)
(ii) (-1,3), (4, 0)
(iii) (\(\frac{1}{2}, \frac{1}{3}\)), (\(\frac{1}{3}, \frac{1}{2}\))
(iv) (0,-3), (-4, 0)
(v) (-1,-2), (3, -1)
(vi) (a, b), (c, d)
(vii) (-2, 1), (-3, -4)
(viii) (at₁², 2at₁), (at₂², 2at₂)
ସମାଧାନ :
P (x,, y,) ଓ Q(x, y) ହେଲେ PQର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ = (\(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\))
(i) P (3, 4) ଓ Q (1, -2) PQର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{3+1}{2}, \frac{4+(-2)}{2}\)) = (2, 1)
(ii) (-1,3) ଓ (4, 0)ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{-1+4}{2}, \frac{3+0)}{2}\)) = \(\frac{3}{2}, \frac{3}{2}\)
(iii) (\(\frac{1}{2}, \frac{1}{3}\)) ଓ (\(\frac{1}{3}, \frac{1}{2}\))ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ \(\left(\frac{\frac{1}{2}+\frac{1}{3}}{2}, \frac{\frac{1}{3}+\frac{1}{2}}{2}\right)=\left(\frac{5}{12}, \frac{5}{12}\right)\)
(iv) (0,-3) ଓ (-4,0)ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{1-4}{2}, \frac{-3+0}{2}\)) = (-2, \(\frac{-3}{2}\))
(v) (-1, -2) ଓ (3, -1)ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{-1+3}{2}, \frac{-2-1}{2}\)) = (1, \(\frac{-3}{2}\))
(vi) (a, b) ଓ (c, d)ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{a+c}{2}, \frac{b+d}{2}\))
(vii) (-2, 1) ଓ (-3, -4)ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{-1+3}{2}, \frac{-2-1}{2}\)) = (1, \(\frac{-3}{2}\))
(viii) (at₁², 2at₁) ଓ (at₂², 2at₂)ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ \(\left(\frac{{at}_1^2+{at}_2^2}{2}, \frac{2 {at}_1+2 {at}_2}{2}\right)\) = (\(\frac{a({t}_1^2+{t}_2^2)}{2}\), a(t₁+t₂))

Question 3.
ନିମ୍ନଲିଖତ ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନରେ ଦତ୍ତ ଦୁଇବିନ୍ଦୁକୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ହେଉଛି (-1, 2) । ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ । ଓ kର ମାନ ନିର୍ଣ୍ଣୟ କର ।
(i) (h, -1), (2, k)
(ii) (5, 3), (h, k)
(iii) (1+h, k), (k, -h – 1)
(iv) (h – k, k – h), (2h, 2k)
ସମାଧାନ :
(i) (h, 1 ) ଓ (2, k) ବିନ୍ଦୁଦ୍ଵୟକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (-1, 2) ।
∴ \(\frac{h+2}{2}\) = -1 ⇒ h + 2 = -2 ⇒ h = -4
ଏବଂ \(\frac{-1+k}{2}\) = 2 ⇒ -1 + k = 4 ⇒ k = 5
∴ h ଓ kର ମାନ ଯଥାକ୍ରମେ – 4 ଓ 5 ।

(ii) 5, 3) ଓ (h, k) ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (-1, 2) ।
∴ \(\frac{5+h}{2}\) = -1 ⇒ 5 + h = -2 ⇒ h = -7
ଏବଂ \(\frac{3+k}{2}\) = 2 ⇒ 3 + k = 4 ⇒ k = 1
∴ h ଓ kର ମାନ ଯଥାକ୍ରମେ – 7 ଓ 1 ।

(iii) (1+h, k), (k, – h – 1) ବିଦୁ୍ୟଦ୍ୱୟକୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (-1, 2) ।
\(\frac{1+h+k}{2}\) = -1 ⇒ 1 + h + k = -2 ⇒ h + k = -3
ଏବଂ \(\frac{k-h-1}{2}\) = 2 ⇒ k – h – 1 = 4 ⇒ k – h = 5
ସମୀକରଣ (i) ଓ (ii) କୁ ଯୋଗକଲେ,

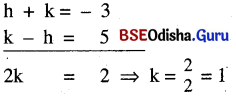
kର ମାନ ସମୀକରଣ (i)ରେ ପ୍ରୟୋଗ କଲେ, h + k = – 3
⇒ h + 1 = -3 ⇒ h – 1 – 3 = -4
∴ h = -4 ଓ k = 1

(iv) (h – k, k – h), (2h, 2k) ବିନ୍ଦୁଦ୍ଵୟକୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (-1, 2) ।
\(\frac{h-k+2h}{2}\) = -1 ⇒ 3h – k = -2 ……(i)
ଏବଂ \(\frac{k-h-1}{2}\) = 2 ⇒ 3k – h = 4 …….(ii)

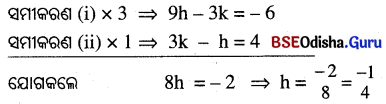
hର ମାନ ସମୀକରଣ (i)ରେ ପ୍ରୟୋଗ କଲେ, 3h – k = -2
⇒ \(\frac{-3}{4}\) – k = -2 = -k = -2 + \(\frac{-3}{4}\) = \(\frac{-8+3}{4}=\frac{-5}{4}\) ⇒ k = \(\frac{5}{4}\)
∴ h = \(\frac{-1}{4}\) ଓ k = \(\frac{5}{4}\)

Question 4.
(0, 0) ଏକ ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ । ଯଦି ରେଖାଖଣ୍ଡର ଏକ ପ୍ରାନ୍ତବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (2, 3) ହୁଏ, ତେବେ ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁଟିର ସ୍ଥାନଙ୍କ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ଏକ ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, 0) ଏବଂ ଏକ ପ୍ରାନ୍ତ ବିଦୁର ସ୍ଥାନାଙ୍କ (2, 3) ।
ମନେକର ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ।
ପ୍ରଶାନୁସାରେ, \(\frac{x+2}{2}\) = 0 ଏବଂ \(\frac{y+3}{2}\) = 0 ⇒ x = – 2 ଏବଂ y = -3
∴ ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) = (-2, -3)

Question 5.
ଏକ ରେଖାଖଣ୍ଡର ଏକ ପ୍ରାନ୍ତବିନ୍ଦୁ ଓ ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (-2, 4) ଏବଂ (1, 2), ତେବେ ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁଟିର ସ୍ଥାନଙ୍କ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ଏକ ରେଖାଖଣ୍ଡର ଏକ ପ୍ରାନ୍ତବିନ୍ଦୁ ଓ ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (-2, 4) ଓ (1, 2) ।
ମନେକର ଅନ୍ୟ ପ୍ରାନ୍ତ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ।
ପ୍ରଶାନୁସାରେ, \(\frac{-2+x}{2}\) = 1 ⇒ x = 2 + 2 = 4 ଏବଂ \(\frac{4+ y}{2}\) = 2 ⇒ y = 4 – 4 = 0
∴ ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (4, 0) ।

Question 6.
ଗୋଟିଏ ରେଖାଖଣ୍ଡର ଏକ ପ୍ରାନ୍ତବିନ୍ଦୁ ଓ ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (3, 5) ଏବଂ (2, 1) ହେଲେ, ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁଟିର ସ୍ଥାନଙ୍କ ସ୍ଥିର କର ।
ସମାଧାନ :
ଗୋଟିଏ ରେଖାଖଣ୍ଡର ଏକ ପ୍ରାନ୍ତବିନ୍ଦୁ ଓ ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (3, 5) ଏବଂ (2, 1) |
ମନେକର ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ।
ପ୍ରଶାନୁସାରେ, \(\frac{x+3}{2}\) = 2 ⇒ x = 4 – 3 = 1 ଏବଂ \(\frac{y+5}{2}\) = 1 ⇒ y = 2 – 5 = -3
∴ ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (1, -3) ।

Question 7.
x ଓ yର କେଉଁ ମୂଲ୍ୟ ପାଇଁ (6, -2) ଓ (2, -4) ବିନ୍ଦୁଦ୍ଵୟକୁ ସଂଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡ ଏବଂ (x, 1) ଓ (-2, y) ବିନ୍ଦୁଦ୍ଵୟକୁ ସଂଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରିବେ ।
ସମାଧାନ :
ଗୋଟିଏ ରେଖାଖଣ୍ଡ PQର ପ୍ରାନ୍ତବିନ୍ଦୁଦ୍ଵୟର ସ୍ଥାନାଙ୍କ P(6, – 2) ଓ Q(2, – 4) ।
ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{6+2}{2}, \frac{-2-4}{2}\)) = (4, -3)
ଅନ୍ୟ ଏକ ରେଖାଖଣ୍ଡ \(\bar{RS}\)ର ପ୍ରାନ୍ତବିନ୍ଦୁ ଦ୍ବୟର ସ୍ଥାନାଙ୍କ R(x, 1) ଓ S(-2, y) ।
RS ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{x+(-2)}{2}, \frac{y+1}{2}\)) ।
PQ ଓ \(\bar{RS}\) ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରିବେ ।
ଅର୍ଥାତ୍ ରେଖାଖଣ୍ଡ ଦ୍ଵୟର ମଧ୍ୟବିନ୍ଦୁ ଅଭିନ୍ନ ଅଟେ ।
ପ୍ରଶାନୁସାରେ, \(\frac{x+(-2)}{2}\) = 4 ⇒ x = 8 + 2 = 10 ଏବଂ \(\frac{1+y}{2}\) = -3 ⇒ y = – 6 – 1 = -7
∴ x = 10 ଓ y = -7।

Question 8.
(2, 3) ଓ (1, 4) ବିନ୍ଦୁଦ୍ଵୟକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡକୁ 3 : 2 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥିବା ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
A (x₁, y₁) ଓ B(x₂,y₂) ବିନ୍ଦୁଦ୍ଵୟର ସଂଯୋଗକାରୀ ରେଖାଖଣ୍ଡ \(\bar{AB}\) କୁ m : n ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥିବା
ବିଦୁର ସ୍ଥାନାଙ୍କ (x, y) = \(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}\right)\)
(2, 3) ଓ (1, 4) ବିନ୍ଦୁଦ୍ଵୟକୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡକୁ 3 : 2 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥ‌ିବା ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ହେଉ ।
ଏଠାରେ x₁ = 2, y₁ = 3, x₂ = 1, y₂ = 4; m = 3 ଓ n = 2
x-ସ୍ଥାନାଙ୍କ = \(\frac{m x_2+n x_1}{m+n}=\frac{3×1+2×2}{3+2}=\frac{3+4}{5}=\frac{7}{5}\)
y-ସ୍ଥାନାଙ୍କ = \(\frac{m y_2+n y_1}{m+n}=\frac{3×4+2×3}{3+2}=\frac{12+6}{5}=\frac{18}{5}\)
∴ (2, 3) ଓ (1, 4) ରେଖାଖଣ୍ଡକୁ 3 : 2 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥିବା ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{7}{5}, \frac{18}{5}\))

Question 9.
(-2, 3) ଓ (5, -7) ବିନ୍ଦୁଦ୍ଵୟକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡକୁ 3 : 4 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥିବା ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ମନେକର (-2, 3) ଓ (5, -7) ବିନ୍ଦୁଦ୍ୱୟକୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡକୁ 3 : 4 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥିବା ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ।
ଏଠାରେ x₁ = -2, y₁ = 3, x₂ = 5, y₂ = -7; m = 3, n = 4 ।
∴ x-ସ୍ଥାନାଙ୍କ = \(\frac{m x_2+n x_1}{m+n}=\frac{3×5+4×(-2)}{3+4}=\frac{15-8}{7}=\frac{7}{7}=1\)
y-ସ୍ଥାନାଙ୍କ = \(\frac{m y_2+n y_1}{m+n}=\frac{3×(-7)+4(3)}{3+4}=\frac{-21+12}{7}=\frac{-9}{7}\)
∴ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥିବା ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (1, \(\frac{-9}{7}\)) ।

Question 10.
ଯଦି (5, 9) ବିନ୍ଦୁଟି, (7, -3) ଓ (4, k)କୁ ସଂଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡକୁ 2 : 1 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରେ, ତେବେ kର ମୂଲ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
(7, -3) ଓ (4, k) କୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡକୁ 2 : 1 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥିବା ବିନ୍ଦୁଟି (5, 9) ।
ଏଠାରେ x₁ = 7, y₁ = -3, x₂ = 4, y₂ = k; m = 2, n = 1
y-ସ୍ଥାନାଙ୍କ = \(\frac{m y_2+n y_1}{m+n}=\frac{2k+1(-3)}{2+1}\)
ପ୍ରଶାନୁସାରେ, \(\frac{2k+1(-3)}{2+1}\) = 9 = 2k – 3 = 9 × 3
⇒ 2k = 27 + 3 = 30 ⇒ k = \(\frac{30}{2}\) = 15
∴ kର ମୂଲ୍ୟ 15 ଅଟେ ।

Question 11.
ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି ସାହାଯ୍ୟରେ ପ୍ରମାଣ କର ଯେ, କୌଣସି ତ୍ରିଭୁଜର ମଧ୍ଯମାତ୍ରୟ ଏକ ବିନ୍ଦୁଗାମୀ ।
ସମାଧାନ :
ମନେକର ABC ତ୍ରିଭୁଜର A, B ଓ C ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ A (x₁,y₁), B (x₂, y₂) ଓ C (x₃, y₃) ।
ABC ତ୍ରିଭୁଜର ମଧ୍ଯମାତ୍ରୟ AD, BE, CF । BC ର ମଧ୍ୟବିନ୍ଦୁ D।
∴ D ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{x_2+x_3}{2}, \frac{y_2+y_3}{2}\)) ।
ସେହିପରି E ଓ F ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ
E(\(\frac{x_1+x_3}{2}, \frac{y_1+y_3}{2}\)), F(\(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\)) ।

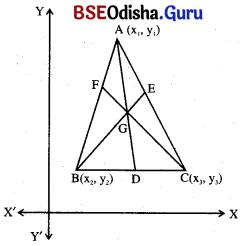
ମଧ୍ୟମାତ୍ରୟର ଛେଦବିନ୍ଦୁ Gକୁ ତ୍ରିଭୁଜର ଭରକେନ୍ଦ୍ର କୁହାଯାଏ । ଭରକେନ୍ଦ୍ରଠାରେ ମଧ୍ୟମାତ୍ରୟ 2 : 1 ଅନୁପାତରେ ପରସ୍ପରକୁ ଅନ୍ତର୍ବିଭକ୍ତ କରନ୍ତି ।

∴ ତିନୋଟି ମଧ୍ଯମାଉପରିସ୍ଥ ଓ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଅଭିନ୍ନ ଅଟେ । ଏଥୁରୁ ସ୍ପଷ୍ଟ ଯେ କୌଣସି ତ୍ରିଭୁଜର ମଧ୍ଯମାତ୍ରୟ ଏକ ବିନ୍ଦୁଗାମୀ ।

Question 12.
(h, 5), (-4, k) ଓ (8, 9) ବିନ୍ଦୁମାନଙ୍କଦ୍ୱାରା ଗଠିତ ତ୍ରିଭୁଜର ଭରକେନ୍ଦ୍ରର ସ୍ଥାନାଙ୍କ (-2, 6) ହେଲେ h ଓ kର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ :
(h, 5), (-4, k) 8 (8, 9) ବିନ୍ଦୁମାନଙ୍କଦ୍ୱାରା ଗଠିତ ତ୍ରିଭୁଜର ଭରକେନ୍ଦ୍ରର ସ୍ଥାନାଙ୍କ (-2, 6) ।
ଏଠାରେ x₁ = h, x₂, = – 4, x₃ = 8, y₁ = 5, y₂ = k, y₃ = 9
ଭରକେନ୍ଦ୍ରର ସ୍ଥାନାଙ୍କ (\(\frac{x_1+x_3+x_3}{3}, \frac{y_1+y_3+y_3}{3}\)
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{x_1+x_3+x_3}{3}=-2\) ଏବଂ \(\frac{y_1+y_3+y_3}{3}\) = 6
⇒ \(\frac{h-4+8}{3}=-2\) ⇒ \(\frac{5+k+9}{3}=6\)
⇒ h + 4 = -6 ⇒ k + 14 = 18
⇒ h = -6 – 4 =- 10 ⇒ k = 18 – 14 = 4
∴ h = 10 ଓ k = 4 ।

Question 13.
∆ ABCର ଭରକେନ୍ଦ୍ରର ସ୍ଥାନାଙ୍କ (1, 1) । A (3, -4), B (-4, 7) ହେଲେ, C ବିନ୍ଦୁର ସ୍ଥାନଙ୍କ ସ୍ଥିର କର ।
ସମାଧାନ :
∆ ABCର ଭରକେନ୍ଦ୍ରର ସ୍ଥାନାଙ୍କ (1, 1) । A ଓ B ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ A (3, -4) ଓ B(-4, 7) ।
ମନେକର ୯ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ।
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{3+(-4)+x}{3}=1\) ଏବଂ \(\frac{-4+7+y}{3}=1\)
⇒ -1 + x = 3 ⇒ y + 3 = 3
⇒ x = 3 + 1 = 4 ⇒ y = 3 – 3 = 0
∴ C ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ C (4, 0) ।

Question 14.
ଗୋଟିଏ ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ମାନ (-4, 1) ଓ (3,-4) ଏବଂ (1, 3) ହେଲେ, ଏହାର ଭରକେନ୍ଦ୍ର ସ୍ଥାନାଙ୍କ ହେବ ।
ସମାଧାନ :
ଗୋଟିଏ ∆ ର ଶୀର୍ଷବିଦୁ୍ୟତ୍ରୟର ସ୍ଥାନାଙ୍କ ( 4, 1), (3, -4) ଏବଂ (1, 3) ।
ଏହାର ଭରକେନ୍ଦ୍ରର ସ୍ଥାନାଙ୍କ x = \(\frac{-4+3+1}{3}=\frac{0}{3}=0\) ଏବଂ y = \(\frac{1-4+3}{3}=\frac{4-4}{3}=0\)
∴ ∆ର ଭରକେନ୍ଦ୍ରର ସ୍ଥାନାଙ୍କ (0, 0) ଅର୍ଥାତ୍ ମୂଳବିନ୍ଦୁ ଅଟେ । (ପ୍ରମାଣିତ)

Question 15.
A ଓ B ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (1, 2) ଓ (5, -4) । AB ରେଖାଖଣ୍ଡ ଉପରେ ଏକ ବିନ୍ଦୁ ସ୍ଥିର କର, ଯେପରି ବିନ୍ଦୁଟିର A ବିନ୍ଦୁଠାରୁ ଦୂରତା, B ବିନ୍ଦୁଠାରୁ ଦୂରତାର 3 ଗୁଣ ହେବ ।
ସମାଧାନ :
AB ର A ଓ B ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (1, 2) ଓ (5,-4) ।
AB ଉପରେ ଏକ ବିନ୍ଦୁ P ଯେପରି AP = 3 BP ⇒ AP : BP=3 : 1
ଏଠାରେ x₁ = 1, y₁ = 2, x₂ = 5, y₂ = -4; m = 3, n = 1

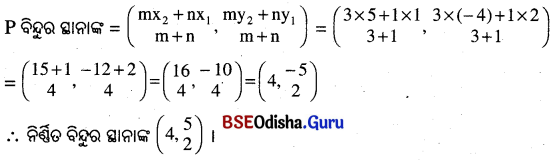
Question 16.
(1, 5) ଓ (7, 2) ସ୍ଥାନାଙ୍କ ବିଶିଷ୍ଟ ବିଦୁ୍ୟଦ୍ୱୟକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡକୁ ସମତ୍ରିଖଣ୍ଡ କରୁଥିବା ବିନ୍ଦୁଦ୍ବୟର ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
AB ର A ଓ B ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (1, 5) ଓ (7, 2) ।
ମନେକର AB କୁ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରୁଥିବା ବିଦୁ୍ୟଦ୍ଵୟ P ଏବଂ Q ।

∴ (1, 5) ଓ (7, 2) ସ୍ଥାନାଙ୍କ ବିଶିଷ୍ଟ ବିଦୁ୍ୟତ୍ବକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡକୁ ସମତ୍ରିଖଣ୍ଡ କରୁଥିବା ବିଦୁ୍ୟଦ୍ୱୟର ସ୍ଥାନାଙ୍କ (3, 4) ଏବଂ (5, 3) ।

Question 17.
O(0, 0), A (2a, 0) ଓ B (0, 2b) ହେଲେ ଦର୍ଶାଅ ଯେ OAB ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ଏବଂ ଏହାର କର୍ଣ୍ଣର ମଧ୍ୟବିନ୍ଦୁ ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁମାନଙ୍କଠାରୁ ସମାନ ଦୂରରେ ଅବସ୍ଥିତ ।
ସମାଧାନ :
∆ OABର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟର ସ୍ଥାନାଙ୍କ ଠ(0, 0), A(2a, 0) ଓ B (0, 2b) ।
A ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (2a, 0) ଏହା x-ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ OA = 2a ଏକକ ।
B ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, 2b) ଏହା y-ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ OB = 2b ଏକକ !
⇒ କର୍ଣ୍ଣ AB = \(\sqrt{(0-2a)^2 +(2b-0)^2}\) = \(\sqrt{4a^2 +4b^2}\) = 2\(\sqrt{a^2 +b^2}\)

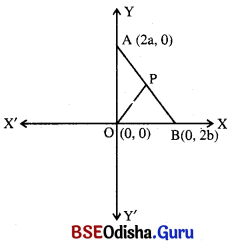
ମନେକର କର୍ପୂର ମଧ୍ୟବିନ୍ଦୁ P ।
AP = BP = \(\frac{\sqrt{a^2 +b^2}}{2}\) = \(\sqrt{a^2 +b^2}\)
∴ P ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{2a+0}{2}, \frac{0+2b}{2}\)) = (a,b)
∴ OP = \(\sqrt{a^2 +b^2}\)
∴ AP = BP = OP ଏଥରୁ ପ୍ରମାଣିତ ଯେ, କର୍ପୂର ମଧ୍ୟବିନ୍ଦୁ P ସମକୋଣୀ ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁମାନଙ୍କଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।

Question 18.
ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି ସାହାଯ୍ୟରେ ପ୍ରମାଣ କର ଯେ, ଏକ ସାମାନ୍ତରିକ ଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।
ସମାଧାନ :
ପ୍ରଦତ୍ତ ଚିତ୍ରରେ OABC ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । ମୂଳବିନ୍ଦୁ Oର ସ୍ଥାନାଙ୍କ (0, 0) ।
ମନେକର OA = a ∴ A ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (a, 0) ।
C ବିନ୍ଦୁରୁ OA ପ୍ରତି CD ଲମ୍ବ ଅଙ୍କନ କରାଯାଉ ।
ମନେକର CD = b ଏବଂ OD = p ।
∴ C ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (p, b) ଏବଂ B ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (a + p, b) ।
ବର୍ତ୍ତମାନ OABC ସାମାନ୍ତରିକ ଚିତ୍ରର ଶୀର୍ଷବିନ୍ଦୁଗୁଡ଼ିକର ସ୍ଥାନାଙ୍କ O (0, 0), A (a, 0), B (a + p, b), C (p, b) ।

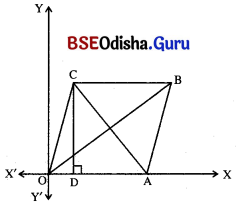
∴ କର୍ଣ୍ଣ AC ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{a+p}{2}, \frac{o+b}{2}\)) = (\(\frac{a+p}{2}, \frac{b}{2}\))
କର୍ଣ୍ଣ OBର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{a+p+0}{2}, \frac{b+0}{2}\)) = (\(\frac{a+p}{2}, \frac{b}{2}\))
∴ ସାମାନ୍ତରିକ ଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟର ମଧ୍ୟବିନ୍ଦୁରୁ ସ୍ଥାନଙ୍କ ଅଭିନ୍ନ ।
ଅର୍ଥାତ୍ କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି । (ପ୍ରମାଣିତ)

Question 19.
ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି ସାହାଯ୍ୟରେ ଦର୍ଶାଅ ଯେ, ଗୋଟିଏ ଆୟତଚିତ୍ରର କଣ୍ଠଦ୍ଵୟ ସର୍ବସମ ଏବଂ ପରସ୍ପରକୁ
ସମାଧାନ :
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ OABC ଏକ ଆୟତଚିତ୍ର ।
OABC ଆୟତଚିତ୍ରର ଶୀର୍ଷବିନ୍ଦୁ ଚାରୋଟିର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ
O (0, 0), A (0, a), B (a, b), C (0, b) ।

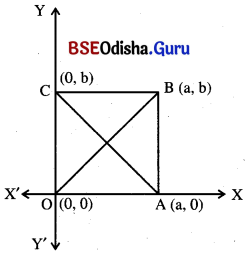
କର୍ଣ୍ଣ AC = \(\sqrt{(0 – a)^2 + (b – 0)^2}\) = \(\sqrt{a^2 +b^2}\)
କର୍ଣ୍ଣ OB = \(\sqrt{(a-0)^2+(b-0)^2}\)= \(\sqrt{a^2 +b^2}\)
∴ AC = OB
କର୍ଣ୍ଣ ACର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{0+a}{2}, \frac{b+0}{2}\)) = (\(\frac{a}{2}, \frac{b}{2}\))
କର୍ଣ୍ଣ OB ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{a+0}{2}, \frac{b+0}{2}\)) = (\(\frac{a}{2}, \frac{b}{2}\))
∴ OABC ଆୟତଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ସର୍ବସମ ଏବଂ ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।

Question 20.
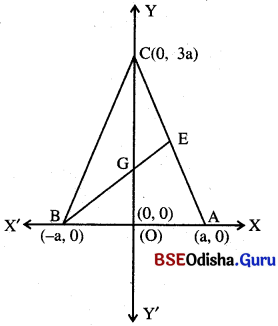
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ABC ଏକ ସମବାହୁ ତ୍ରିଭୁଜ । A ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (a, 0) ହେଲେ,
(i) ଅନ୍ୟ ଶୀର୍ଷବିନ୍ଦୁଦ୍ଵୟର ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କର ।
(ii) ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
(iii) BE ମଧ୍ଯମାର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
(iv) G ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କର ।

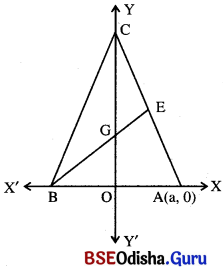
ସମାଧାନ :
ଦତ୍ତ ଚିତ୍ରରେ ABC ଏକ ସମବାହୁ ତ୍ରିଭୁଜ । A ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (a, 0) ।
∴ CO ⊥ AB ⇒ ABର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, 0) ।
ମନେକର \(\frac{a+x}{2}=0\) ⇒ x = -a
\(\frac{0+y}{2}=0\) ⇒ y = 0
∴ Bବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (-a, 0) ।

ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ (AB)
\(\sqrt{{a-(-a)}^2 +(0-0)^2}\) = √(2a)² = = √4a² = 2a
∴ ସମବାହୁ ତ୍ରିଭୁଜର ଉଚ୍ଚତା (OC)
= ବାହୁର ଦୈର୍ଘ୍ୟ × \(\frac{\sqrt{3}}{2}\) = 2a × \(\frac{\sqrt{3}}{2}\) = √3a
∴ C ବିନ୍ଦୁଟି y ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ ହେତୁ ଏହାର y ସ୍ଥାନାଙ୍କ 0 ।
C ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, √3a) ।
(i) ସମବାହୁ ତ୍ରିଭୁଜର ଅନ୍ୟ ଶୀର୍ଷବିନ୍ଦୁ ଦ୍ବୟର ସ୍ଥାନାଙ୍କ B (-a, 0) ଏବଂ C (0, √3a) ।
(ii) ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ = 2a
(iii)

(iv)