Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 4 ତ୍ରିକୋଣମିତି Ex 4(c) Textbook Exercise Questions and Answers.
BSE Odisha Class 10 Maths Solutions Geometry Chapter 4 ତ୍ରିକୋଣମିତି Ex 4(c)
Question 1.
ଗୋଟିଏ ବୃକ୍ଷର ପାଦଦେଶ ସହ ଏକ ସମତଳରେ ଏବଂ ଏହାଠାରୁ 120 ମିଟର ଦୂରରେ ଅବସ୍ଥିତ କୌଣସି ବିନ୍ଦୁରେ ବୃକ୍ଷର ଅଗ୍ରଭାଗର କୌଣିକ ଉନ୍ନତିର ପରିମାଣ 30° ହେଲେ ବୃକ୍ଷର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
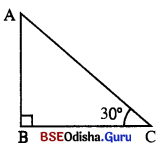
ପାଣଣ୍ଠ ତିତ୍ରରେ ମନେକର AB ବଘର କଲତା |
BC = ବୃକ୍ଷର ପାଦଦେଶଠାରୁ C ବିନ୍ଦୁର ଦୂରତ୍ବ = 120 ମିଟର
C ଠାରେ A ବିନ୍ଦୁର କୌଣିକ ଉନ୍ନତି = 30°, ଅର୍ଥାତ୍ m∠ACB = 30° |
ABC ସମକୋଣା ତ୍ରିଭୁଇରେ , tan 30° = \(\frac { AB }{ BC }\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac { AB }{ 120 }\) ⇒ AB = \(\frac{120}{\sqrt{3}}\) ମି.
⇒ AB = \(\frac{120 \sqrt{3}}{3}\) ମି. = 40√3 ମି. = 40 × 1.732 ମି. = 69.28 ମି.
![]()
Question 2.
27 ମିଟର ଉଚ୍ଚ ଏକ ବତୀଘରର ଶୀର୍ଷରୁ ଏକ ଜାହାଜର କୌଣିକ ଅବନତିର ପରିମାଣ 30° । ବତୀଘରଠାରୁ ଜାହାଜର ଦୂରତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ମନେକର AB ବତୀଘରର ଉଚ୍ଚତା = 27 ମି.
ବତୀଘର ଶୀର୍ଷ Aରୁ ଏକ ସମତଳରେ ଅବସ୍ଥିତ ଜାହାଜର କୌଣିକ ଅବନତି 30° |
∵ m∠DAC 30°
ବତୀଘରଠାରୁ ଜାହାଜର ଦୂରତା = BC
ଏଠାରେ \(\overline{\mathrm{BC}}\) ||\(\overline{\mathrm{AD}}\), \(\overline{\mathrm{AC}}\) ଛେଦକ ।
∴ m∠DAC = m∠ACB = 30° (ଏକାନ୍ତ୍ରର)
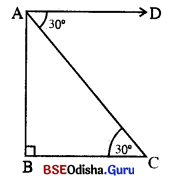
ABC ସମକୋଣା ତ୍ରିରୁ କାଲେ tan 30° = \(\frac { AB }{ BC }\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac { 27 }{ BC }\) = 27√3 ମି. = 27 × 1.732 = 46.76 ମି.
∴ ବତୀଘରଠାରୁ ଜାହାଜର ଦୂରତା 46.76 ମିଟର ।
Question 3.
2 ମିଟର ଉଚ୍ଚ ଏକ ଦର୍ଶକ ଦେଖିଲା ଯେ, 24 ମିଟର ଦୂରରେ ଥିବା ଏକ ସ୍ତମ୍ଭର କୌଣିକ ଉନ୍ନତିର ପରିମାଣ 30° । ସ୍ତମ୍ଭର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ, ମନେକର ସ୍ତମ୍ଭର ଉଚ୍ଚତା AB |
CD = ଦର୍ଶକର ଉଚ୍ଚତା = 2 ମିଟର = BE,
∠ADE = 30°, BC = DE = 24 ମି. ।
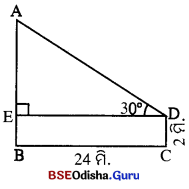
AED ସମକୋଣା ତ୍ରିରୁ କାଲେ, tan 30° = \(\frac { AE }{ DE }\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac { AE }{ 24 }\) ⇒ AE = \(\frac{24}{\sqrt{3}}\) ମି. = \(\frac{24 \sqrt{3}}{3}\) ମି. = 8√3 ମି.
= 8 × 1.732 ମି. = 13.86 ମି. |
∴ ସ୍ତମ୍ଭର ଉଚ୍ଚତା = AB = AE + BE = 13.86 ମି. + 2 ମି. = 15.86 ମି.
∴ ସ୍ତମ୍ଭର ଉଚ୍ଚତା 1586 ମିଟର ।
Question 4.
ଏକ ସିଡ଼ି ଏକ କାନ୍ଥର ଶୀର୍ଷକୁ ସ୍ପର୍ଶ କରୁଅଛି । ସିଡ଼ର ପାଦଦେଶରୁ କାନ୍ଥର ଦୂରତା 3 ମିଟର । ସିଡ଼ିଟି ଭୂମି ସହ 60° ରେ ଆନତ । ସିଡ଼ିର ଦୈର୍ଘ୍ୟ ସ୍ଥିର କର ।
Solution:
ପାଣଣ୍ଠ ଚିତ୍ରରେ, କାନ୍ତର ଇଲତା = AB ଓ ପତିର ବୈଶ୍ୟ = AC |
BC = ସିଡ଼ିର ପାଦଦେଶରୁ କାନ୍ଥର ଦୂରତା = 3 ମି.,
କାନ୍ଥଟି ଭୂମି ସହ ଲମ୍ବଭାବରେ ଥିବାରୁ m∠ABC = 90°
ସିଡ଼ିଟି ଭୂମି ସହ ଅଙ୍କନ କରିଥିବା କୋଣର ପରିମାଣ = 60°,
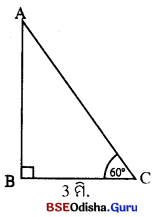
ABC ସିଡ଼ିର ଦୈର୍ଘ୍ୟ 6 ମିଟର cos 60° = \(\frac { BC }{ AC }\)
⇒ \(\frac { 1 }{ 2 }\) = \(\frac { 3 }{ AC }\) ⇒ AC = 2 × 3 = 6 ମି.
∴ ସିତିର ଦେଶ୍ୟ 6 ମିଟର |
![]()
Question 5.
15 ମିଟର ଉଚ୍ଚ ଜଣେ ଦର୍ଶକ ଏକ କୋଠାଘରଠାରୁ 12 ମିଟର ଦୂରସ୍ଥ ଏକ ବିନ୍ଦୁରୁ ଦେଖୁଲା ଯେ, କୋଠାଘରର ଶୀର୍ଷର କୌଣିକ ଉନ୍ନତିର ପରିମାଣ 60° । କୋଠାଘରର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ, AB = କୋଠାଘରର ଉଚ୍ଚତା |
CD = ଦର୍ଶକର ଉଚ୍ଚତା 1-5 ମିଟର = BM,
∠ACM = 60°, BD = MC = 12 ମିଟର ।
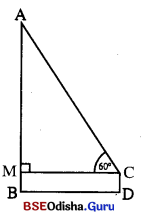
AMC ସମକୋଣା ତ୍ରିଭୁକରେ tan 60° = \(\frac { AM }{ MC }\) ⇒ √3 = \(\frac { AM }{ 12 }\)
⇒ AM = 12 √3 = 12 × 1.732 = 20.78 ମି.
∴ କୋଠାଘରର ଉଚ୍ଚତା = AB = AM + MB = 20.78 + 1.5 = 22.28 ମିଟର ।
Question 6.
ସୂର୍ଯ୍ୟର କୌଣିକ ଉନ୍ନତିର ପରିମାଣ 60° ବେଳେ ଗୋଟିଏ ଗଛର ଛାଇର ଦୈର୍ଘ୍ୟ 15 ମିଟର ଥିଲା । ଗଛର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
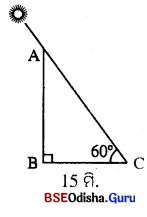
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ, ଗଛର ଉଚ୍ଚତା = AB | ଗଛର ଛାଇର ଦୈର୍ଘ୍ୟ = BC = 15 ମି. |
ସୂର୍ଯ୍ୟର କୌଣିକ ଉନ୍ନତି 60° ଅର୍ଥାତ୍ m∠ACB = 60° |
ABC ସମକୋଣା ତ୍ରିରୁ କାଲେ
⇒ tan C = \(\frac { AB }{ BC }\)
⇒ tan 60° = \(\frac { AB }{ 15 }\) ⇒ √3 = \(\frac { AB }{ 15 }\)
⇒ AB = 15√3 ମି. = 15 × 1.732 = 25.98 ମି. |
∴ ଗାଛ୍ର ରକତା 25.98 ମିଟର |
Question 7.
300 ମି. ଉଚ୍ଚ ଏକ ପାହାଡ଼ ଉପରୁ ଏକ ସମତଳରେ ଅବସ୍ଥିତ ଗୋଟିଏ ସ୍ତମ୍ଭର ଶୀର୍ଷ ଓ ପାଦଦେଶର କୌଣିକ ଅବନତିର ପରିମାଣ ଯଥାକ୍ରମେ 30° ଓ 60° ହେଲେ ସ୍ତମ୍ଭର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
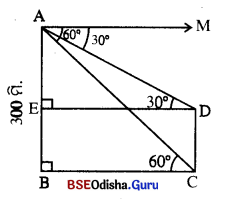
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ, ପାହାଡ଼ର ଉଚ୍ଚତା = AB = 300 ମି.
ଓ ସ୍ତମ୍ଭର ଉଚ୍ଚତା = CD |
ପାହାଡ଼ ଓ ସ୍ତମ୍ଭ ମଧ୍ଯରେ ଦୂରତା = BC = DE, m∠ACB = 60° (ଏକାନ୍ତର)
ଓ m∠MAD = m∠ADE = 30° (ଏକାନ୍ତର) , CD = BE
ABC ସମକୋଣୀ ତ୍ରିଭୁଜରେ , tan C = \(\frac { AB }{ BC }\)
⇒ tan 60° = \(\frac { 300 }{ BC }\) ⇒ √3 = \(\frac { 300 }{ BC }\)
⇒ BC = \(\frac{300}{\sqrt{3}}\) = 100√3 ମି. |
∴ BC = DE = 100√3 ମି.
AED ସମକୋଣୀ ତ୍ରିଭୁଜରେ tan D = \(\frac { AE }{ ED}\)
⇒ tan 30° = \(\frac{\mathrm{AE}}{100 \sqrt{3}}\) ⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{\mathrm{AE}}{100 \sqrt{3}}\) ⇒ AE = \(\frac{100 \sqrt{3}}{\sqrt{3}}\) = 100 ମି. |
CD = BE = AB – AE = (300 – 100) ମି. = 200 ମି.
∴ ସ୍ତମ୍ଭର ଉଚ୍ଚତା 200 ମିଟର ।
Question 8.
ସୂର୍ଯ୍ୟର କୌଣିକ ଉନ୍ନତିର ପରିମାଣ 60° ରୁ 45° କୁ ହ୍ରାସ ପାଇଥିବାରୁ ଏକ ସ୍ତମ୍ଭର ଛାଇର ଦୈର୍ଘ୍ୟ 24 ମିଟର ବୃଦ୍ଧି ପାଇଲା । ସ୍ତମ୍ଭର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
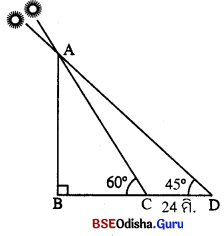
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ, ସ୍ତମ୍ଭର ଉଚ୍ଚତା = AB ।
ସୂର୍ଯ୍ୟର କୌଣିକ ଉନ୍ନତି 60° ବେଳେ AB ସ୍ତମ୍ଭର ଛାଇର ସୂର୍ଯ୍ୟର କୌଣିକ BC |
ସୂର୍ଯ୍ୟର କୌଣିକ ଉନ୍ନତି 45° ବେଳେ AB ସ୍ତମ୍ଭର ଛାଇର ସୂର୍ଯ୍ୟର କୌଣିକ BD |
m∠ACB = 60° ଓ m∠ADB = 45°, CD = 24 ମି.
ମନେକର BC = x ମି. BD = BC + CD = (x + 24) ମି.
ABC ସମକୋଣା ତ୍ରିଭୁଜରେ, tan C = \(\frac { AB }{ BC }\)
⇒ tan 60° = \(\frac { AB }{ BC }\) ⇒ √3 = \(\frac { AB }{ x }\) ⇒ AB = √3x ମି. |
ABD ସମକୋଣା ତ୍ରିଭୁଜରେ, tan D = \(\frac { AB }{ BD }\)
⇒ tan 45° = \(\frac{\sqrt{3} x}{x+24}\) ⇒ 1 = \(\frac{\sqrt{3} x}{x+24}\)
⇒ √3x = x + 24 ⇒ √3x – x = 24 ⇒ x (√3x – 1) = 24
⇒ x = \(\frac{24}{\sqrt{3}-1}\) = \(\frac{24(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}\) = \(\frac{24(\sqrt{3}+1)}{3-1}\)
= \(\frac{24(\sqrt{3}+1)}{2}\) = 12 (√3x + 1) ମି. |
∴ ପ୍ତମ୍ନର ଉକତା = AB = √3x = √3 × 12 (√3x + 1)
= (36 + 12√3) ମି. = 36 + 12 × 1.732 = 36 + 20.784 = 56.784 ମି. |
∴ ପ୍ତମ୍ନର ଉକତା 56.78 ମି. |
Question 9.
ଏକ ସମତଳ ଭୂମି ଉପରେ 40 ମିଟର ବ୍ୟବଧାନରେ ଦୁଇଟି ଖୁଣ୍ଟ ଲମ୍ବଭାବରେ ପୋତାଯାଇଛି । ଗୋଟିଏ ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁରେ ଯେଉଁ କୋଣ ଉତ୍ପନ୍ନ କରନ୍ତି, ସେମାନେ ପରସ୍ପର ଅନୁପୂରକ । ଖୁଣ୍ଟଦ୍ଵୟର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
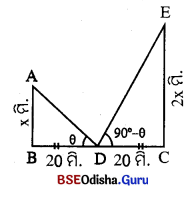
ପାର୍ଶ୍ଵସ୍ଥ ଚିତ୍ରରେ, ସାନ ଖୁଣ୍ଟର ଉଚ୍ଚତା = AB ଓ ବଡ଼ ଖୁଣ୍ଟର ଉଚ୍ଚତା = EC । ଖୁଣ୍ଟଦ୍ଵୟ ମଧ୍ଯରେ ଦୂରତା = BC = 40 ମି. |
ମନେକର AB = x ମି., ତେବେ EC = 2x ମି. |
BD = CD = \(\frac { 40 }{ 2 }\) = 20 ମି. | m∠ADB + m∠EDC = 90°
ମନେକର m∠ADB = θ |
ତେବେ m∠EDC = 90° – θ
ABD ସମକୋଣା ତ୍ରିଭୁଜରେ, tan θ = \(\frac { AB }{ BD }\)
⇒ tan θ = \(\frac { x }{ 20 }\)
ECD ସମକୋଣା ତ୍ରିଭୁଜରେ, tan (90° – θ) = \(\frac { EC }{ CD }\)
⇒ cot θ = \(\frac { 2x }{ 20 }\) = \(\frac { x }{ 10 }\) ⇒ tan θ = \(\frac { 10 }{ x }\)
(i) ଓ (ii) ରୁ \(\frac { x }{ 20 }\) = \(\frac { 10 }{ x }\) ⇒ x2 = 200
⇒ x = √200 = 10√2 ମି. |
∴ AB ଖୁଣର ଉକତା = x = 10√2 ମି. |
ଓ EC ଖୁଣର ଉକତା = 2x = 10√2 × 2 ମି. = 20√2 ମି. |
![]()
Question 10.
ଗୋଟିଏ ଗଛର ଶୀର୍ଷରୁ ଭୂମି ଉପରେ ଥିବା ଗୋଟିଏ ବସ୍ତୁର କୌଣିକ ଅବନତିର ପରିମାଣ 60° ଥିଲା । ସେହି ଗଛର ଶୀର୍ଷରୁ 15 ମିଟର ତଳକୁ ଓହ୍ଲାଇଆସିଲେ ଉକ୍ତ ବସ୍ତୁର କୌଣିକ ଅବନତିର ପରିମାଣ 30° ହୁଏ । ଗଛର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
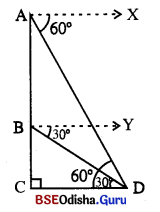
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ, ମନେକର ଗଛର ଉଚ୍ଚତା AC = x ମିଟର, AB = 15 ମିଟର । ସୁତରାଂ BC = (x – 15) ମିଟର ।
ବସ୍ତୁର ଅବସ୍ଥିତି D ହେଉ । CD ସହିତ \(\overrightarrow{\mathrm{AX}}\) ଓ \(\overrightarrow{\mathrm{BY}}\) ସମାନ୍ତର ସରଳରେଖା ଅଙ୍କନ କର । ପ୍ରଶ୍ନନୁସାରେ, A ଓ B ଠାରେ କୌଣିକ ଅବନତି m∠XAD = 60°
ଓ m∠YBD = 30° |
AX ଓ BY ରକାଯେ CD ସଦୃ ମାମାକୁର ହୋଇ ଥିବାରୁ m∠YBD = 30° ଓ m∠CDB = 30° |
ବର୍ତ୍ତମାନ ACD ସମକୋଣୀ ତ୍ରିଭୁଜରେ \(\frac { AC }{ CD }\) = tan 60° ⇒ \(\frac { x }{ CD }\) = √3
⇒ CD = \(\frac{x}{\sqrt{3}}\)
BCD ସମକୋଣୀ ତ୍ରିଭୁଜରେ \(\frac { BC }{ CD }\) = tan 30° ⇒ \(\frac { x – 15 }{ CD }\) = \(\frac{1}{\sqrt{3}}\)
⇒ CD = (x – 15) √3
(i) ଓ (ii) ଉଭୟରୁ \(\frac{x}{\sqrt{3}}\) = (x −15) √3
⇒ 3 (x – 15) = x ⇒ 3x – 45 = x
⇒ 2x = 45 ଦା x = \(\frac { 45 }{ 2 }\) = 22\(\frac { 1 }{ 2 }\)
∴ ଗଛର ଉଚ୍ଚତା 22.5 ମିଟର ।
Question 11.
10 ମିଟର ଉଚ୍ଚ ଏକ ସ୍ତମ୍ଭର ଅଗ୍ରଭାଗରୁ ଏକ ସମତଳରେ ଅବସ୍ଥିତ ଗୋଟିଏ ମନ୍ଦିରର ଶୀର୍ଷର କୌଣିକ ଉନ୍ନତିର ପରିମାଣ ଓ ପାଦଦେଶର କୌଣିକ ଅବନତିର ପରିମାଣ ଯଥାକ୍ରମେ 45° ଓ 30° ହୋଇଯାଏ । ମନ୍ଦିରର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
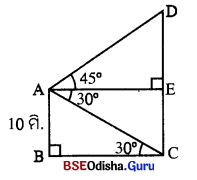
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ, ସ୍ତମ୍ଭର ଉଚ୍ଚତା = AB = 10 ମି. । ମନ୍ଦିରର ଉଚ୍ଚତା = DC
ସ୍ତମ୍ଭ ଓ ମନ୍ଦିର ମଧ୍ୟରେ ଦୂରତା = BC = AE I ସ୍ତମ୍ଭର ଶୀର୍ଷ Aରୁ
ଏକ ସମତଳରେ ଅବସ୍ଥିତ ମନ୍ଦିରର ଶୀର୍ଷ Dର କୌଣିକ ଉନ୍ନତି 45° ।
ଆଥାତ; m∠DAE = 45°, m∠EAC = m∠ACB = 30°
AB = CE = 10 ମି. BC = AE
AED ସମକୋଣା ତ୍ରିଭୁଜରେ, tan A = \(\frac { DE }{ AE }\)
⇒ tan 45° = \(\frac{\mathrm{DE}}{10 \sqrt{3}}\) ⇒ 1 = \(\frac{\mathrm{DE}}{10 \sqrt{3}}\) ⇒ DE = 10√3 ମି. |
DC = DE + CE = 10√3 + 10 = 10 × 1.732 + 10 = 17.32 + 10 = 27.32 ମି. |
∴ ଗଛର ଉଚ୍ଚତା 27.32 ମିଟର ।
Question 12.
12 ମିଟର ପ୍ରସ୍ଥ ଏକ ରାସ୍ତାର ଏକ ପାର୍ଶ୍ଵରେ ଥିବା ଏକ କୋଠାଘର, ଏହାର ଅପରପାର୍ଶ୍ବରେ ଥିବା ଅନ୍ୟ ଏକ ଘରର ଝରକାରେ ଏକ ସମକୋଣ ସୃଷ୍ଟି କରେ । କୋଠାଘରର ପାଦଦେଶରେ ଝରକାର କୌଣିକ ଉନ୍ନତିର ପରିମାଣ 30° ହେଲେ କୋଠାଘରର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
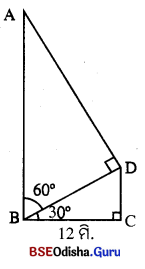
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ, ରାସ୍ତାର ପ୍ରସ୍ଥ = BC = 12 ମି. |
କୋଠାଘରର ଉଚ୍ଚତା = AB |
ଅପର ପାର୍ଶ୍ଵରେ ଥିବା ଝରକାର ଅବସ୍ଥାନ = D |
m∠ADB = 90°, m∠CBD = 30°, m∠ABC = 90°
m∠ABD = 90°, m∠ABC – m∠CBD = 90° – 30° = 60°
BCD ସମକୋଣୀ ତ୍ରିଭୁଜରେ , cos 30° = \(\frac { BC }{ BD }\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac { 12 }{ BD }\) ⇒ BD = \(\frac{24}{\sqrt{3}}\) = 8√3 ମି. |
ABD ସମକୋଣୀ ତ୍ରିଭୁଜରେ , cos 60° = \(\frac { BC }{ BD }\)
= \(\frac { 1 }{ 2 }\) = \(\frac{8 \sqrt{3}}{A B}\) ⇒ AB = 16√3 = 16 × 1.732 = 27.71 ମି. |
∴କୋଠାଘରର ଉଚ୍ଚତା 27.71 ମି. |
Question 13.
ଜଣେ ଲୋକ ଗୋଟିଏ ନଦୀ କୂଳରେ ଠିଆ ହୋଇ ଦେଖୁଲା ଯେ, ନଦୀର ଅପର ପାର୍ଶ୍ୱସ୍ଥ ଭୂମିରେ ଥିବା ଗୋଟିଏ ଦୁର୍ଗର କୌଣିକ ଉନ୍ନତିର ପରିମାଣ 60° | ଦୁର୍ଗ ସହିତ ଏକ ସରଳରେଖାରେ ମିଟର 60 ପଛକୁ ଘୁଞ୍ଚିଆସି ଦେଖୁଲା ଯେ, ଉକ୍ତ କୌଣିକ ଉନ୍ନତିର ପରିମାଣ 45° ହେଲା । ନଦୀର ପ୍ରସ୍ଥ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ, ଦୁର୍ଗର ଉଚ୍ଚତା = AB | ଲୋକଟି ବିନ୍ଦୁରେ ଠିଆ ହୋଇଥିଲା । A ବିନ୍ଦୁରେ C ର କୌଣିକ ଉନ୍ନତିର ପରିମାଣ 60° ଓ D ର କୌଣିକ ଉନ୍ନତିର ପରିମାଣ 45° |
ଅଥାତ୍ ; m∠ACB = 60° ଓ m∠ADB = 45°, CD = 60° ମି |
ମନେକର BC = x ମି |
BD = BC + CD = (x + 60) ମି
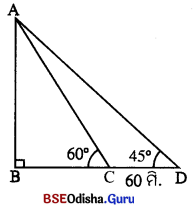
ABC ସମକୋଣା ତ୍ରିଭୁଜରେ, tan C = \(\frac { AB }{ BC }\)
⇒ tan 60° = \(\frac { AB }{ x }\) ⇒ √3 = \(\frac { AB }{ x }\) ⇒ AB = √3x ମି |
ABD ସମକୋଣା ତ୍ରିଭୁଜରେ, tan D = \(\frac { AB }{ BD }\)
⇒ tan 45° = \(\frac{\sqrt{3} x}{x+60}\)
⇒ 1 = \(\frac{\sqrt{3} x}{x+60}\)
⇒ √3x = x + 60
⇒ √3x – x = 60
⇒ x (√3 – 1) = 60
⇒ x = \(\frac{60}{\sqrt{3}-1}\) = \(\frac{60(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}\) = \(\frac{60(\sqrt{3}+1)}{(\sqrt{3})^2-(1)^2}\) = \(\frac{60(\sqrt{3}+1)}{3-1}\) = 30 (√3x + 1) ମି |
= 30 (1.732 + 1) ମି = 30 × 2.732 = 81.96 ମି |
Question 14.
ଦୁଇଟି ସ୍ତମ୍ଭ ପରସ୍ପରଠାରୁ 12 ମିଟର ଦୂରରେ ଏକ ସମତଳ ଉପରେ ଅବସ୍ଥିତ । ଗୋଟିକର ଉଚ୍ଚତା ଅନ୍ୟଟିର ଦୁଇଗୁଣ । ସ୍ତମ୍ଭଦ୍ବୟର ପାଦବିନ୍ଦୁକୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁରୁ ଦେଖିଲେ ସ୍ତମ୍ଭଦ୍ଵୟର ଶୀର୍ଷବିନ୍ଦୁଦ୍ଵୟର କୌଣିକ ଉନ୍ନତି ପରସ୍ପର ଅନୁପୂରକ ହୁଏ, ସ୍ତମ୍ଭନ୍ୱୟର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ, ସ୍ତମ୍ଭଦ୍ବୟର ଉଚ୍ଚତା ଯଥାକ୍ରମେ AB ଓ ED ସ୍ତମ୍ଭଦ୍ବୟ ମଧ୍ୟରେ ଦୂରତା = BD = 12 ମି |
BC = CD = \(\frac { 12 }{ 2 }\) = 6 ମି
ଯଦି m∠ECD = θ° ହୁଏ, ତେବେ m∠ACB = 90° – θ° ହେବ |
ମନେକର ED = x ମି ତେବେ, AB = 2x ମି (∵ AB = 2ED)
ECD ସମକୋଣା ତ୍ରିଭୁଜରେ, tan θ = \(\frac { ED }{ CD }\) ⇒ tan θ = \(\frac { x }{ 6 }\)
ABC ସମକୋଣା ତ୍ରିଭୁଜରେ, tan (90° – θ) = \(\frac { AB }{ BC }\)
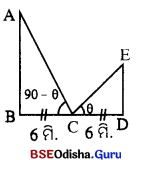
⇒ cot θ = \(\frac { 2x }{ 6 }\) ⇒ \(\frac { 1 }{ tan θ }\) = \(\frac { 2x }{ 6 }\)
⇒ tan θ = \(\frac { 3 }{ x }\)
(i) ଓ (ii) ର \(\frac { x }{ 6 }\) = \(\frac { 3 }{ x }\) ⇒ x2 = 18
⇒ x = √18 = 3√2 ମି , ED = x = 3√2 ମି
AB = 2x = 2 × 3√2 = 6√2 ମି
∴ ସମଦ୍ଵୟର ରକ୍ତା ଯଥାକୃଣେ 6√2 ମି ଓ 3√2 ମି |
Question 15.
ଗୋଟିଏ ଦୁର୍ଗର ପାଦଦେଶ ସହ ଏକ ସରଳରେଖାରେ ଥିବା ଦୁଇଟି ବିନ୍ଦୁରୁ ଦୁର୍ଗର ଶୀର୍ଷଭାଗର କୌଣିକ ଉନ୍ନତିର ପରିମାଣ ଯଥାକ୍ରମେ 30° ଓ 45° । ଦୁର୍ଗର ଉଚ୍ଚତା 30 ମିଟର ହେଲେ, ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ୟରେ ବ୍ୟବଧାନ କେତେ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ, ଦୁର୍ଗର ଉଚ୍ଚତା AB = 30 ମିଟର ।
m∠ACB ଓ m∠ADB ଯଥାକ୍ରମେ C ଓ D ଦିନ୍ଦୁରୁ ଦୁଗର ଶୀର୍ଷ Aର କୌଣିକ ଉନ୍ନତି ଦତ୍ତ ଅଛି । ସେଗୁଡ଼ିକ ହେଲା –
m∠ACB = 45°, m∠ADB = 30°, ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ଯରେ ଦୂରତା CD ।
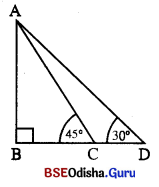
ABC ସମକୋଣା ତ୍ରିଭୁଜରେ, tan 45° = \(\frac { AB }{ BC }\)
⇒ 1 = \(\frac { 30 }{ BC }\) ⇒ BC = 30 ମିଟର ।
ABD ସମକୋଣା ତ୍ରିଭୁଜରେ, tan 30° = \(\frac { AB }{ BD }\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac { 30 }{ BD }\) ⇒ 30√3 – 30
= (√3 – 1) = 30 (1.732 – 1) = 30 × 0. 732 = 21.96 ମିଟର ।
Question 16.
ଗୋଟିଏ କୋଠାର ଉଚ୍ଚତା 12 ମିଟର । କୋଠାର ଶୀର୍ଷରୁ ଏକ ସମତଳରେ ଅବସ୍ଥିତ ଏକ ସ୍ତମ୍ଭର ଶୀର୍ଷ ଓ ପାଦଦେଶର କୌଣିକ ଉନ୍ନତି ଓ ଅବନତିର ପରିମାଣ ଯଥାକ୍ରମେ 60° ଓ 30° । ସ୍ତମ୍ଭର ଉଚ୍ଚତା ଓ କୋଠାଘର ଠାରୁ ସ୍ତମ୍ଭର ଦୂରତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ, କୋଠାର ଉଚ୍ଚତା AB = 12 ମି. । ମନେକର ସ୍ତମ୍ଭର ଉଚ୍ଚତା CD = x ମିଟର
∠DAE, A ବିନ୍ଦୁରୁ D ର କୌଣିକ ଉନ୍ନତି
∠EAC, A ବିନ୍ଦୁରୁ C ବିନ୍ଦୁର କୌଣିକ ଅବନତି ।
m∠DAE = 60°, m∠EAC = m∠ACB = 30° (ଏକାନ୍ତର)
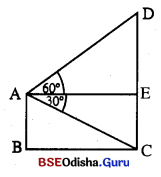
ABC ସମକୋଣୀ ତ୍ରିଭୁଜରେ tan 30° = \(\frac { AB }{ BC }\) ⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac { 12 }{ BC }\)
⇒ BC = 12√3 = 12 × 1.732 = 20.78 ମିଟର ।
DAE ସମକୋଣା ତ୍ରିଭୁଜରେ, tan 60° = \(\frac { DE }{ AE }\)
⇒ √3 = x – 12 ⇒ x = 48 ମିଟର |
∴ ସ୍ତମ୍ଭର ଉଚ୍ଚତା 48 ମିଟର ଓ କୋଠାଘର ଠାରୁ ସ୍ତମ୍ଭର ଦୂରତା 20-78 ମିଟର ।
