BSE Odisha 9th Class Maths Solutions Algebra Chapter 5 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 5(a)

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter Chapter 5 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 5(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 5 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 5(a)

Question 1.
ଭୁଲ୍ ଥିଲେ ଠିକ୍ କର ।

(i) ମୂଳ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, 0) ।
ସମାଧାନ:
ଠିକ୍ ଅଛି ।

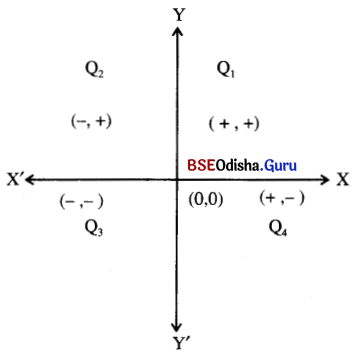
(ii) ପ୍ରଥମ ପାଦ (Q₁) ଉପରିସ୍ଥ (x, y)ରେ x > 0, y < 0 ।
ସମାଧାନ:
ପ୍ରଥମ ପାଦ (Q₁) ଉପରିସ୍ଥ (x, y)ରେ x > 0, y > 0
ଅଥବା ଚତୁର୍ଥ ପାଦ (Q₄) ଉପରିସ୍ଥ (x, y)ରେ x > 0, y < 0

(iii) ଦ୍ଵିତୀୟ ପାଦ (Q₂) ଉପରିସ୍ଥ (x, y) ରେ x < 0, y < 0 
ସମାଧାନ:
ଦ୍ଵିତୀୟ ପାଦ (Q₂) ଉପରିସ୍ଥ (x, y) ରେ x < 0, y > 0
ଅଥବା ତୃତୀୟ ପାଦ (Q₃) ଉପରିସ୍ଥ (x, y) ରେ x < 0, y < 0 

(iv) ତୃତୀୟ ପାଦ (Q₃) ଉପରିସ୍ଥ (x, y) ରେ x < 0, y < 0 
ସମାଧାନ:
ଠିକ୍ ଅଛି ।

(v)  ଚତୁର୍ଥ ପାଦ (Q₄) ଉପରିସ୍ଥ (x, y) ରେ x > 0 , y > 0 ।
ସମାଧାନ:
ପ୍ରଥମ ପାଦ (Q₁) ଉପରିସ୍ଥ (x, y) ରେ x > 0, y > 0
ଅଥବା ଚତୁର୍ଥ ପାଦ (Q₄) ଉପରିସ୍ଥ (x, y) ରେ x > 0 , y < 0 l

(vi) x-ଅକ୍ଷ ଉପରିସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, y) ।
ସମାଧାନ:
x-ଅକ୍ଷ ଉପରିସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, 0) ।
ଅଥବା y- ଅକ୍ଷ ଉପରିସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, y) ।

(vii) y- ଅକ୍ଷ ଉପରିସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, 0) ।
ସମାଧାନ:
y-ଅକ୍ଷ ଉପରିସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, y) ।
ଅଥବା x-ଅକ୍ଷ ଉପରିସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, 0) ।

(viii) Q₁ ∪ Q₂ ∪ Q₃ ∪ Q₄ = R²
ସମାଧାନ:
Q₁ ∪ Q₂ ∪ Q₃ ∪ Q₄ ∪ {(x, 0) : x ∈ R} ∪ {(0, y) : y ∈ R} = R²

(ix) R² ର ଦକ୍ଷିଣ ଅର୍ଥ ସମତଳ = Q₁ ∪ Q₂
ସମାଧାନ:
R² ର ଊର୍ଦ୍ଧ୍ବ ଅର୍ଥ ସମତଳ = Q₁ ∪ Q₂

(x) R² ର ଦକ୍ଷଶ ଅକ୍ଷ ସମତଳ ।
ସମାଧାନ:
R² ର ଦକ୍ଷିଣ ଅର୍ଥ ସମତଳ = Q₃ ∪ Q₄
ଅଥବା R² ର ଊର୍ଦ୍ଧ୍ବ ଅର୍ଷ ସମତଳ = Q₁ ∪ Q₂

(xi) (-3, -2) ବିନ୍ଦୁଟି ଦ୍ବତୀୟ ପାଦରେ ଅବସ୍ଥିତ ।
ସମାଧାନ:
ଠିକ୍ ଅଛି ।

(xii) (1.2, -1) ବିନ୍ଦୁଟି ଦ୍ବିତୀୟ ପାଦରେ ଅବସ୍ଥିତ ।
ସମାଧାନ:
(1.2, -1) ବିନ୍ଦୁଟି ଚତୁର୍ଥ ପାଦରେ ଅବସ୍ଥିତ ।

(xiii) (-0.5 , √2) ବିନ୍ଦୁଟି ପ୍ରଥମ ପାଦରେ ଅବସ୍ଥିତ ।
ସମାଧାନ:
(-0.5 , √2) ବିନ୍ଦୁଟି ଦ୍ବିତୀୟ ପାଦରେ ଅବସ୍ଥିତ ।

(xiv) (x, y) = (-2, 3) ହେଲେ, x = -2 ଓ y = 3
ସମାଧାନ:
ଠିକ୍ ଅଛି ।

Question 2.
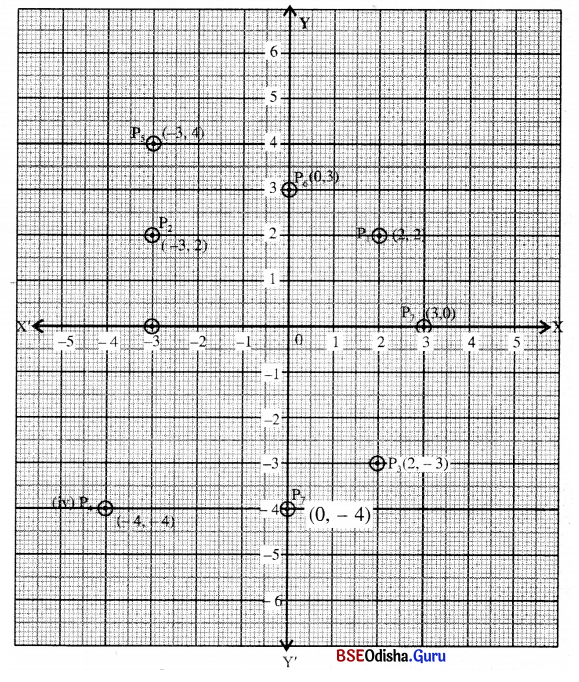
ସମତଳରେ x- ଓ y- ଅକ୍ଷ ଅଙ୍କନ କରି ନିମ୍ନଲିଖତ ବିନ୍ଦୁମାନଙ୍କୁ ଲେଖ କାଗଜ ଉପରେ ଦତ୍ତ କ୍ରମିତ ଯୋଡ଼ି ସାହାଯ୍ୟରେ ଚିହ୍ନଟ କର । (ଲେଖ କାଗଜରେ ପ୍ରତ୍ୟେକ ଅକ୍ଷରେ 1 ସେ.ମି. ଦୈର୍ଘ୍ୟକୁ 1 ଏକକ ନିଅ ।)
(i) P₁(2, 2)
(ii) P₂(-3, 2)
(iii) P₃(2, -3)
(iv) P₄(-4, -4)
(v) P₅(-3, 4)
(vi) P₆(0, 3)
(vii) P₇(3, 0)
(viii) P₈(0, -4)
ଉ – X ଓ Y ଉଭୟ ଅକ୍ଷରେ 1 ସେ.ମି. = 1 ଏକକ ।

Question 3.
ନିମ୍ନଲିଖୂ ପ୍ରଶ୍ନମାନଙ୍କର ଉତ୍ତର ଦିଅ

(i) ସଂଖ୍ୟାରେଖା \(\overleftrightarrow{\mathrm{X}^{\prime} \mathbf{X}}\) ର ମାତ୍ରା କେତେ ?
ସମାଧାନ:
ସଂଖ୍ୟାରେଖା \(\overleftrightarrow{\mathrm{X}^{\prime} \mathbf{X}}\) ଗାେଟିଏ  ର ମାତ୍ରା କେତେ 

(ii) xy- ସମତଳର ମାତ୍ରା କେତେ ?
ସମାଧାନ:
xy- ସମତଳର ଦୁଇଟି ମାତ୍ରା କେତେ 

(iii) ସମତଳ ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି କେଉଁ ଗଣିତଜ୍ଞଙ୍କ ଦ୍ୱାରା ଆବିଷ୍କୃତ ହୋଇଥିଲା ?
ସମାଧାନ:
ସମତଳ ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି ଗଣିତଞ Rene Descartes ଙ୍କ ଦ୍ୱାରା ଆବିଷ୍କୃତ ହୋଇଥିଲା

(iv) xy-ସମତଳ କୁ x-ଅକ୍ଷ ଓ y-ଅକ୍ଷ କେତେଗୋଟି ପାଦରେ ବିଭକ୍ତ କରନ୍ତି ?
ସମାଧାନ:
xy-ସମତଳ କୁ x-ଅକ୍ଷ ଓ y-ଅକ୍ଷ ଚାରୋଟି ପାଦରେ ବିଭକ୍ତ କରନ୍ତି 

(v) \(\overleftrightarrow{\mathrm{X}^{\prime} \mathbf{X}}\) ଅକ୍ଷର ଧନାତ୍ମକ ଦିଗ କେଉଁଟି ?
ସମାଧାନ:
\(\overleftrightarrow{\mathrm{X}^{\prime} \mathbf{X}}\) ଅକ୍ଷର ଧନାତ୍ମକ ଦିଗ \(\overrightarrow{O X}\)

(vi) \(\overleftrightarrow{\mathrm{Y}^{\prime} \mathbf{Y}}\) ଅକ୍ଷର ଋଣାତ୍ମକ ଦିଗ କେଉଁଟି ?
ସମାଧାନ:
\(\overleftrightarrow{\mathrm{Y}^{\prime} \mathbf{Y}}\) ଅକ୍ଷର ଋଣାତ୍ମକ ଦିଗ \(\overrightarrow{\mathrm{OY}^{\prime}}\)

(vii) ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତିରେ ଜ୍ୟାମିତିକ ଚର୍ଚ୍ଚା ପାଇଁ ଗଣିତର କେଉଁ ଶାଖାଟିର ପ୍ରୟୋଗ କରାଯାଇଥାଏ ?
ସମାଧାନ:
ବୀଜଗଣିତ (Algebra)

(viii) P(5, 4) ବିନ୍ଦୁର x-ସ୍ଥାନାଙ୍କ ଓ y-ସ୍ଥାନାଙ୍କ କେତେ ?
ସମାଧାନ:
P(5, 4) ବିନ୍ଦୁର x-ସ୍ଥାନାଙ୍କ 5 ଓ y-ସ୍ଥାନାଙ୍କ 4

Question 4.
A(0, y) , B(7, 0), C(-2, 5), D (3, -4) ଏବଂ E (−1,1) ବିନ୍ଦୁଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁ ବିନ୍ଦୁ ବା ବିନ୍ଦୁଗୁଡ଼ିକ କେଉଁ ବୃତ୍ତପାଦରେ ଅଥବା କେଉଁ କେଉଁ ଅକ୍ଷରେ ଅବସ୍ଥିତ ଲେଖ ।
ସମାଧାନ:
A (0, y) ବିନ୍ଦୁଟି y- ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ। B (7, 0) ବିନ୍ଦୁଟି x- ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ ।
C (–2, 5) ବିନ୍ଦୁଟି ଦ୍ୱିତୀୟ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ । D (3, – 4) ବିନ୍ଦୁଟି ଚତୁର୍ଥ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
E (−1, 1) ବିନ୍ଦୁଟି ଦ୍ୱିତୀୟ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।

Question 5.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) x > 0, y > 0 ହେଲେ, p(x, -y) ________ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
(ii) x < 0, y < 0 ହେଲେ, p(x, -y) ________ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
(iii) x>0, y < 0 ହେଲେ p (−x, y) ________ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
(iv) x ∈ R, y < 0 ହେଲେ, p(x, y) ________ ଅର୍ଷତଳରେ ଅବସ୍ଥିତ ।
(v) x < 0, y = R ହେଲେ, p (x, y) ________ ଅର୍ଷତଳରେ ଅବସ୍ଥିତ ।
(vi) x > 0, y > 0 ହେଲେ, p (-x, -y) ________ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
ସୂଚନା : (ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ର ଦେଖ୍ ଉତ୍ତରଗୁଡ଼ିକୁ ତର୍ଜମା କର ।)

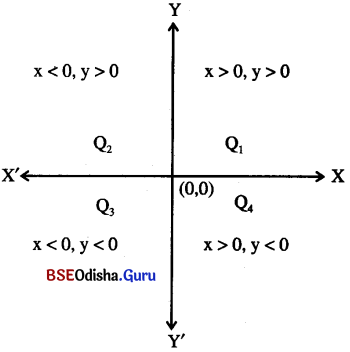
(i) x > 0, y > 0 ହେଲେ, p(x, -y) Q₄ ଚତୁର୍ଥ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
(ii) x < 0, y < 0 ହେଲେ, p(x, -y) Q₂ ଦ୍ୱିତୀୟ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
(iii) x > 0, y < 0 ହେଲେ, P (-x, y) Q₃ ତୃତୀୟ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
(iv) x ∈ R, y < 0 ହେଲେ, P(x, y) ଅଧଃ ଅର୍ଷତଳରେ ଅବସ୍ଥିତ ।
(v) x < 0, y = R ହେଲେ, p (x, y) ବୀମ ଅର୍ଷତଳରେ ଅବସ୍ଥିତ ।
(vi) x > 0, y > 0 ହେଲେ, p (-x, -y) Q₃ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।