BSE Odisha 9th Class Maths Solutions Algebra Chapter 5 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 5(c)

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter Chapter 5 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 5(c) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 5 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 5(c)

Question 1.
ନିମ୍ନଲିଖ୍ ଲେଖଚିତ୍ରଗୁଡ଼ିକ ଅଙ୍କନ କର ।

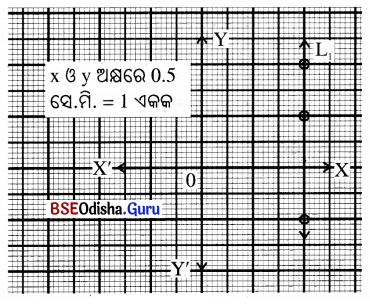
(i) x = 4
ସମାଧାନ:
x = 4 ଦ୍ଵାରା ସୂଚିତ ସରଳରେଖା (L₁)
ମୂଳବିନ୍ଦୁର ଡାହାଣକୁ 4 ଏକକ ଦୂରରେ
y- ଅକ୍ଷ ସହ ସମାନ୍ତର ହୋଇ XY
ସମତଳରେ ଅବସ୍ଥାନ କରିବ ।

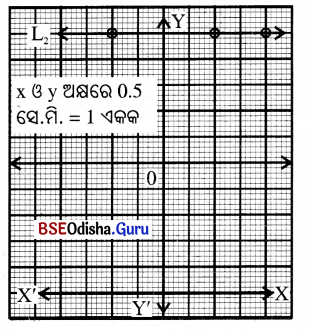
(ii) y = 5
ସମାଧାନ:
y = 5 ଦ୍ଵାରା ସୂଚିତ ସରଳରେଖା (L₂)
ମୂଳବିନ୍ଦୁର ଡାହାଣକୁ 5 ଏକକ ଦୂରରେ
x- ଅକ୍ଷ ସହ ସମାନ୍ତର ହୋଇ 
xy- ସମତଳରେ ଅବସ୍ଥାନ କରିବ ।

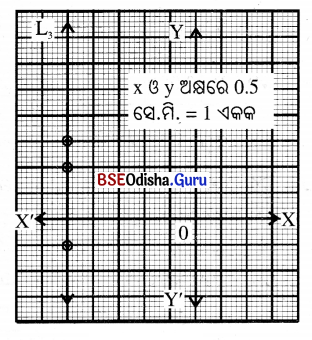
(iii) x = -5
ସମାଧାନ:
x = -5 ଦ୍ଵାରା ସୂଚିତ ସରଳରେଖା (L₃)
ମୂଳବିନ୍ଦୁର ଡାହାଣକୁ -5 ଏକକ ଦୂରରେ
y- ଅକ୍ଷ ସହ ସମାନ୍ତର ହୋଇ 
xy- ସମତଳରେ ଅବସ୍ଥାନ କରିବ ।

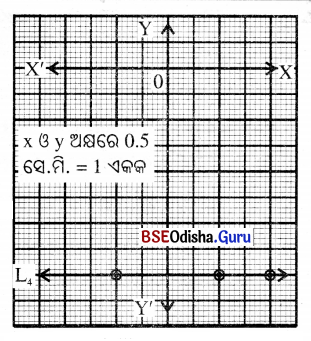
(iv) y = -4
ସମାଧାନ:
y = -4 ଦ୍ଵାରା ସୂଚିତ ସରଳରେଖା (L₄)
ମୂଳବିନ୍ଦୁର ଡାହାଣକୁ -4 ଏକକ ଦୂରରେ
n- ଅକ୍ଷ ସହ ସମାନ୍ତର ହୋଇ 
xy- ସମତଳରେ ଅବସ୍ଥାନ କରିବ ।

Question 2.
ନିମ୍ନଲିଖତ ସମୀକରଣଗୁଡ଼ିକର ଲେଖଚିତ୍ର ଅଙ୍କନ କର ।

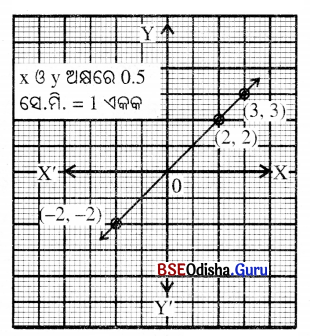
(i) y = x
ସମାଧାନ:

x	-2	2	3
y	-2	2	3

ଏଠାରେ କ୍ରମିତ ଯୋଡ଼ିମାନ (– 2, 2), (2, 2) ଓ (3, 3)
କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ନେଇ ଅଙ୍କନ କଲେ
ଲେଖଚିତ୍ରଟି ଏକ ସରଳରେଖା ହେବ ।

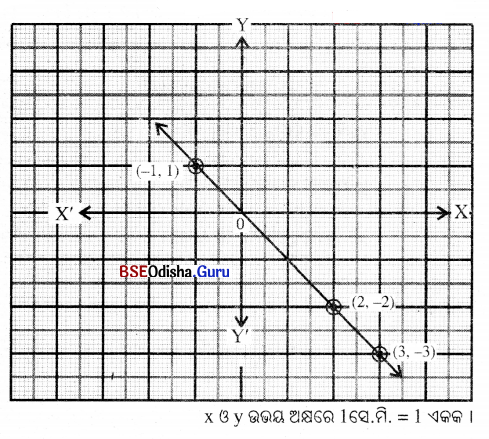
(ii) y + x = 0
ସମାଧାନ:
y + x = 0
⇒ y = -x

x	-1	2	3
y	1	-2	-3

ଏଠାରେ କ୍ରମିତ ଯୋଡ଼ିମାନ (-1, 2), (2, -2) ଓ (3, -3)
କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ନେଇ ଅଙ୍କନ କଲେ
ଲେଖଚିତ୍ରଟି ଏକ ସରଳରେଖା ହେବ ।

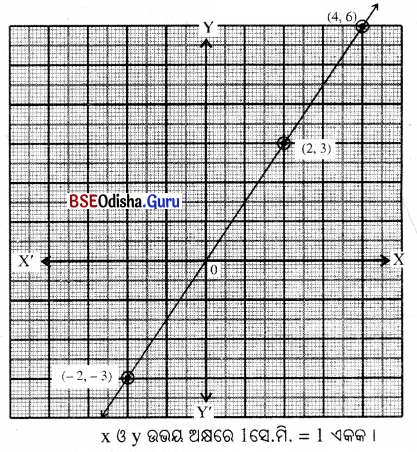
(iii) 2y = 3x
ସମାଧାନ:
2y = 3x
⇒ y = \(\frac{3 x}{2}\)

x	2	-2	4
y	3	-3	6

ଏଠାରେ କ୍ରମିତ ଯୋଡ଼ିମାନ (2, 3), (-2, -3) ଓ (4, 6)
କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ନେଇ ଅଙ୍କନ କଲେ
ଲେଖଚିତ୍ରଟି ଏକ ସରଳରେଖା ହେବ ।

Question 3.
ନିମ୍ନଲିଖତ ସମୀକରଣଗୁଡ଼ିକର ଲେଖଚିତ୍ର ଅଙ୍କନ କର ।

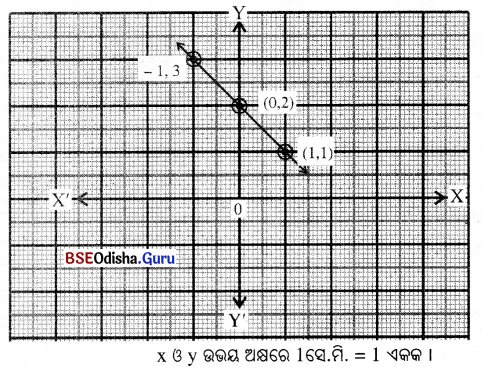
(i) x + y – 2 = 0
ସମାଧାନ:
x + y – 2 = 0
⇒ y = 2 – x

x	0	1	-1
y	2	1	3

ଏଠାରେ କ୍ରମିତ ଯୋଡ଼ି (0, 2), (1, 1) ଓ (-1, 3) 
କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ନେଇ ଅଙ୍କନ କଲେ ଲେଖଚିତ୍ରଟି ଏକ ସରଳରେଖା ହେବ ।

(ii) x + y + 2 = 0
ସମାଧାନ:
x + y + 2 = 0
⇒ y = -2 – x

x	0	1	-1
y	-2	-3	-1

ଏଠାରେ କ୍ରମିତ ଯୋଡ଼ିମାନ (0, -2), (1, -3) ଓ (-1, -1)
କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ନେଇ ଅଙ୍କନ 
କଲେ ଲେଖଚିତ୍ରଟି ଏକ ସରଳରେଖା ହେବ ।

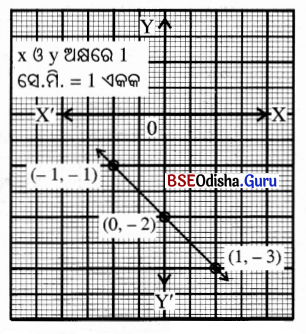
(iii) 2x + y – 2 = 0
ସମାଧାନ:
2x + y – 2 = 0
⇒ y = 2 – 2x

x	0	1	2
y	2	0	-2

ଏଠାରେ କ୍ରମିତ ଯୋଡ଼ିମାନ (0, 2), (1, 0) ଓ (2, -2)
କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ନେଇ ଅଙ୍କନ କଲେ 
ଲେଖଚିତ୍ରଟି ଏକ ସରଳରେଖା ହେବ ।

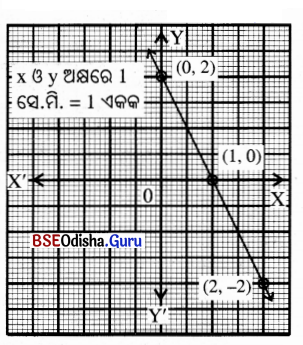
(iv) x + 2y – 3 = 0
ସମାଧାନ:
x + 2y – 3 = 0
⇒ 2y = 3 – x
⇒ y = \(\frac{3-x}{2}\)

x	1	3	-1
y	1	0	2

ଏଠାରେ କ୍ରମିତ ଯୋଡ଼ିମାନ (1, 1), (3, 0) ଓ (-1, 2)
କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ନେଇ ଅଙ୍କନ କଲେ
ଲେଖଚିତ୍ରଟି ଏକ ସରଳରେଖା ହେବ ।

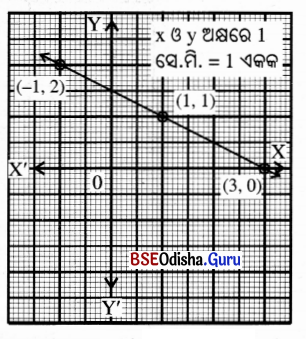
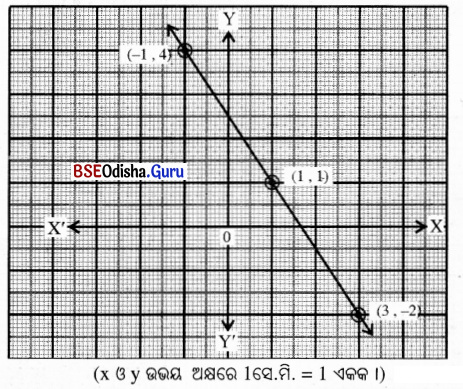
(v) 3x + 2y – 5 = 0
ସମାଧାନ:
3x + 2y – 5 = 0
⇒ 2y = 5 – 3x
⇒ y = \(\frac{5-3x}{2}\)

x	1	3	-1
y	1	-2	4

ଏଠାରେ କ୍ରମିତ ଯୋଡ଼ିମାନ (1, 1), (3, -2) ଓ (-1, 4)
କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ନେଇ ଅଙ୍କନ କଲେ
ଲେଖଚିତ୍ରଟି ଏକ ସରଳରେଖା ହେବ ।

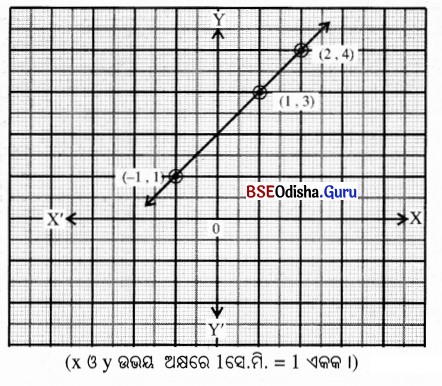
(vi) x – y + 2 = 0
ସମାଧାନ:
x – y + 2 = 0
⇒ x + 2 = y
⇒ y= x + 2

x	1	-1	2
y	3	1	4

ଏଠାରେ କ୍ରମିତ ଯୋଡ଼ିମାନ (1, 3), (-1, 1) ଓ (2, 4)
କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ନେଇ ଅଙ୍କନ କଲେ
ଲେଖଚିତ୍ରଟି ଏକ ସରଳରେଖା ହେବ ।

Question 4.
ଦତ୍ତ ଟେବୁଲର ତଥ୍ୟକୁ ବ୍ୟବହାର କରି ଲେଖଚିତ୍ର ଅଙ୍କନ କର ଏବଂ ଲେଖଚିତ୍ରରୁ à ଓ b ର ମୂଲ୍ୟ ନିରୂପଣ କର ।

x	1	2	5	-1	b
y	3	1	-5	a	-3

ଏଠାରେ କ୍ରମିତ ଯୋଡ଼ିମାନ (1, 3), (2, 1) ଓ (5, -5)
କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ନେଇ ଅଙ୍କନ କଲେ ଲେଖଚିତ୍ରଟି ଏକ ସରଳରେଖା ହେବ ।
ସମାଧାନ:

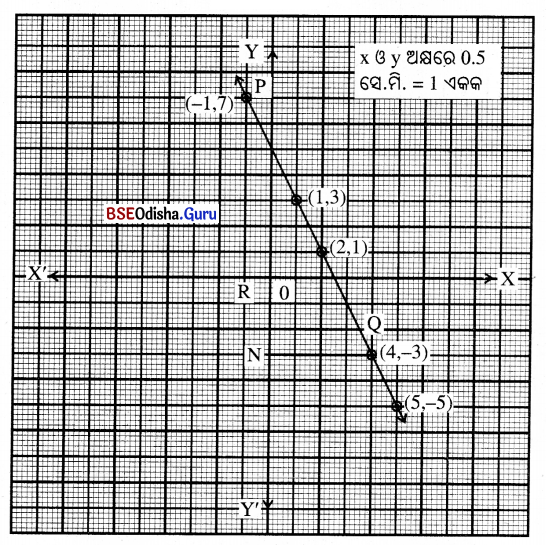
X-ଅକ୍ଷ ଉପରିସ୍ଥ R ବିନ୍ଦୁରେ ଅଙ୍କିତ ଲମ୍ବ ଅଙ୍କିତ ଲେଖଚିତ୍ରକୁ P ବିନ୍ଦୁରେ ଏବଂ Y-ଅକ୍ଷ ଉପରିସ୍ଥ N ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବ ଲେଖଚିତ୍ରକୁ Q ବିନ୍ଦୁରେ ଛେଦକରୁ । P ବିନ୍ଦୁରେ ସ୍ଥାନାଙ୍କ (-1, 7) ଏବଂ ଠୁ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (4, -3) ହେବ  a = 7, b = 4

Question 5.
2x + 3y – 6 = 0 ର ଲେଖଚିତ୍ର ଅଙ୍କନ କରି ଲେଖଚିତ୍ରରୁ ଅକ୍ଷଦ୍ଵୟଙ୍କୁ ଏହା କେଉଁ ବିନ୍ଦୁରେ ଛେଦ କରୁଛି ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
2x + 3y – 6 = 0
⇒ 3y = 6 – 2x ⇒ y = \(\frac{6-2 x}{3}\)

x	0	3	-3
y	2	0	4

ଏଠାରେ କ୍ରମିତ ଯୋଡ଼ିମାନ (0, 2), (3, 0) ଓ (-3, 4)
କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ନେଇ ଅଙ୍କନ କଲେ ଲେଖଚିତ୍ରଟି ଏକ ସରଳରେଖା ହେବ ।

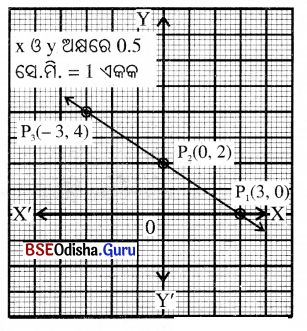
L, 2x + 3y – 6 = 0 ର ଲେଖ । L, x-ଅକ୍ଷକୁ P₁(3, 0) ବିନ୍ଦୁରେ ଓ y-ଅକ୍ଷକୁ P₂(0, 2) ବିନ୍ଦୁରେ ଛେଦକରୁଛି ।

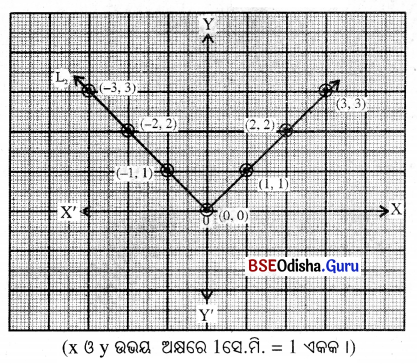
Question 6.
y = |x| ର ଲେଖଚିତ୍ର -5 ≤ x ≤ 3 ପାଇଁ ଅଙ୍କନ କର ।
ସମାଧାନ:
y = |xl (-5 ≤ x ≤ 3)

x	1	2	3	0	-1	-2	-3
y	1	2	3	0	1	2	3

ଏଠାରେ କ୍ରମିତ ଯୋଡ଼ିମାନ (1, 1), (2, 2), (3, 3), (0, 0), (-1, 1), (2, 2) ଓ (-3, 3) 
ଲେଖଚିତ୍ରଟି Q₁ ଓ Q₂ ପାଦରେ ରହିବ ।

Question 7.
x = ± 3, y = ± 4 ଦ୍ୱାରା ସୂଚିତ ଚାରିଗୋଟି ସରଳରେଖା ଅଙ୍କନ କରି ସେମାନଙ୍କ ପାରସ୍ପରିକ ଛେଦ ହେତୁ ଉତ୍ପନ୍ନ ଆୟତ କ୍ଷେତ୍ରର ଶୀର୍ଷବିନ୍ଦୁମାନଙ୍କର ସ୍ଥାନଙ୍କ ନିରୂପଣ କର ।
ସମାଧାନ:
x = ± 3
x = 3

x	3	3	3
y	3	1	4

x = -3

x	-3	-3	-3
y	-2	0	2

y = ± 4
⇒ y = 4

x	-3	0	2
y	4	4	4

y = -4

x	-2	1	3
y	-4	-4	-4

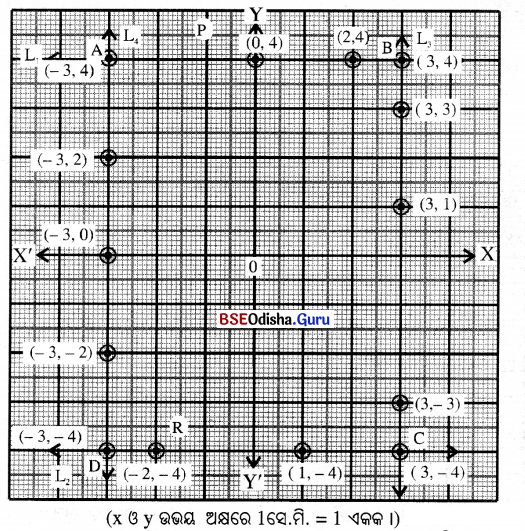
ଦତ୍ତ ଲେଖରେ ABCD ଏକ ଆୟତ କ୍ଷେତ୍ର । ଆୟଷତ୍ରର ଶୀଷିବିନ୍ଦୁମାନଙ୍କର ସ୍ଥାନାଙ୍କ A(-3, 4), B(3, 4), C(3, -4) ଓ D(-3, -4) 

Question 8.
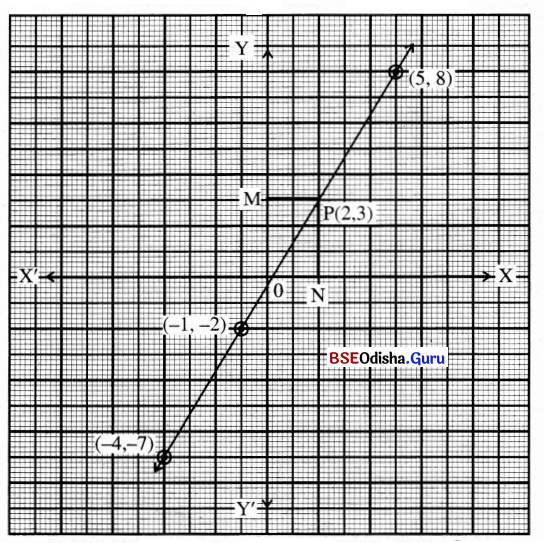
5x – 3y = 1 ସମୀକରଣର ଲେଖଚିତ୍ର ଅଙ୍କନ କର । ଦର୍ଶାଅ ଯେ, P(2,3) ବିନ୍ଦୁଟି ସରଳରେଖା ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ ହେବ ।
ସମାଧାନ:
5x – 3y = 1
⇒ 5x – 1 = 3y ⇒ 3y = 5x – 1 ⇒ y = \(\frac{5 x-1}{3}\)

x	-1	-4	5
y	-2	-7	8

ଏଠାରେ କ୍ରମିତ ଯୋଡ଼ିମାନ (-1, -2), (-4, -7) ଓ (5, 8)
କ୍ରମିତ ଯୋଡ଼ିମାନକୁ ଯୋଗକଲେ ଲେଖଚିତ୍ରଟି ଏକ ସରଳରେଖା ହେବ ।
y-ଅକ୍ଷର 3 ସୂଚକ ବିନ୍ଦୁ M ଏବଂ x-ଅକ୍ଷର2 ସୂଚକ ବିନ୍ଦୁ N ନିଅ ।
M ଓ N ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବ ଲେଖଚିତ୍ରକୁ P ବିନ୍ଦୁରେ ଛେଦକରେ, ଯାହାର ସ୍ଥାନାଙ୍କ P (2, 3) ହେବ । ଅର୍ଥାତ୍ P(2, 3) ବିନ୍ଦୁଟି ସରଳରେଖା ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ ।

Question 9.
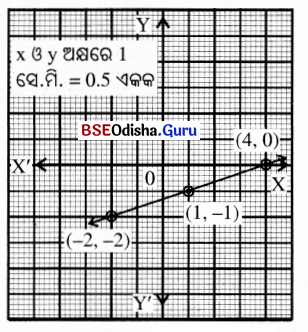
x – 3y = 4 ସମୀକରଣର ଲେଖଚିତ୍ର ଅଙ୍କନ କର । ଲେଖଚିତ୍ରରୁ ଦତ୍ତ କ୍ଷେତ୍ରରେ ବିନ୍ଦୁମାନଙ୍କର ସ୍ଥାନଙ୍କ ସ୍ଥିର କର, ଯେତେବେଳେ (i) y = -1 ଏବଂ (ii) x = -2
ସମାଧାନ:
x – 3y = 4 ⇒ x – 4 = 3y
⇒ 3y = x – 4 ⇒ y = \(\frac{x-4}{3}\)

x	-2	1	4
y	-2	-1	0

L ସରଳରେଖା, x – 3y = 4 ସମୀକରଣର ଲେଖଚିତ୍ର ଅଟେ ।
y = -1 ବେଳେ x = 1
ଦତ୍ତ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (1, -1) ।
ସେହିପରି x = – 2 ବେଳେ y = – 2 ଦତ୍ତ 
ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (– 2, – 2) ।

Question 10.
x = 2y – 1 ଏବଂ 3y = x ସମୀକରଣ ଦ୍ଵୟର ଲେଖଚିତ୍ର ଅଙ୍କନ କରି ଲେଖଚିତ୍ର ଦ୍ୱୟର ଛେଦବିଦୁର ସ୍ଥାନାଙ୍କ ନିରୂପଣ କର ।
ସମାଧାନ:
x = 2y – 1
⇒ 2y = x + 1 ⇒ y = \(\frac{x+1}{2}\)

x	1	3	-1
y	1	2	0

(1, 1), (3, 2), (-1, 0) କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ଯୋଗକଲେ ଏକ ସରଳରେଖା ହେବ ।
3y = x
⇒ y = \(\frac{x}{3}\)

x	3	0	-3
y	1	0	-1

(3, 1), (0, 0), (-3, -1) କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ଯୋଗକଲେ ଏକ ସରଳରେଖା ହେବ ।

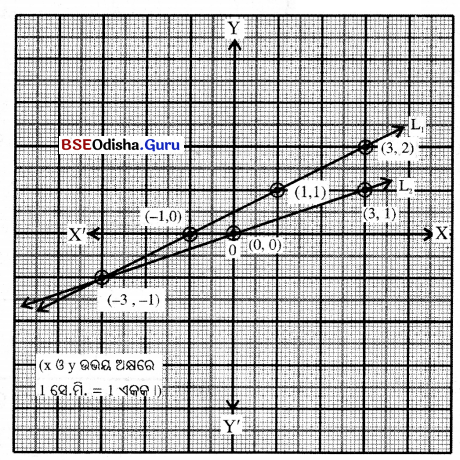
L₁ , x = 2y – 1 ର ଲେଖ ଏବଂ L₂ 3y = x ର ଲେଖ ଅଟେ ।
L₁ ∩ L₂ = {(-3, -1)}
ଲେଖଚିତ୍ର ଦ୍ଵୟର ଚ୍ଛେଦବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ P(-3, -1) ଅଟେ ।