BSE Odisha 10th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(f)

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(f) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(f)

Question 1.
ନିମ୍ନରେ କେତେକ ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ r କିମ୍ବା ବ୍ୟାସ d ଦତ୍ତ ଅଛି । ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଗୋଲକର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ଓ ଆୟତନ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
(i) r = 21 ସେ.ମି.
(ii) d = 14 ସେ.ମି.
(iii) r = 10.5 ସେ.ମି.
Solution:
ଗୋଲକର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 4πr² ବର୍ଗ ଏକକ
ଗୋଲକର ଆୟତନ = \(\frac { 4 }{ 3 }\) πr³ ଘନ ଏକକ

(i) r = 21 ସେ.ମି.
∴ ଗୋଲକର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 4πr² = 4 × \(\frac { 22 }{ 7 }\) × (21)²= 5544 ଦ. ସେ.ମି.
∴ ଗୋଲକର ଆୟତନ = \(\frac { 4 }{ 3 }\) πr³ = \(\frac { 4 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × (21)³
= 4 × 22 × (21)² = 38808 ଶ.ସେ.ମି.

(ii) d = 14 ସେ.ମି. ⇒ r = \(\frac { 14 }{ 2 }\) = 7 ସେ.ମି.
∴ ଗୋଲକର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 4πr² = 4 × \(\frac { 22 }{ 7 }\) × (7)² = 616 ଦ. ସେ.ମି.
∴ ଗୋଲକର ଆୟତନ = \(\frac { 4 }{ 3 }\)πr³ = \(\frac { 4 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × (7)³ = \(\frac{4312}{3}\) = 1437\(\frac { 1 }{ 3 }\) ଦ. ସେ.ମି.

(iii) r = 10.5 ସେ.ମି. = 21 ସେ.ମି..
∴ ଗୋଲକର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 4πr² = 4 × \(\frac { 22 }{ 7 }\) × \(\frac { 21 }{ 2 }\) × \(\frac { 21 }{ 2 }\) = 1386 ଦ. ସେ.ମି.
∴ ଗୋଲକର ଆୟତନ = \(\frac { 4 }{ 3 }\)πr³ = \(\frac { 4 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × (\(\frac { 21 }{ 2 }\))³ = 4851 ଶ.ସେ.ମି.

Question 2.
ନିମ୍ନରେ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ତିନୋଟି ଲେଖାଏଁ ଧାତବ ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ ଦତ୍ତ ଅଛି । ସେଗୁଡ଼ିକୁ ତରଳାଇ ଗୋଟିଏ ଗୋଲକରେ ପରିଣତ କଲେ, ପ୍ରତ୍ୟେକ ସ୍ଥଳେ ନୂତନ ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ କେତେ ହେବ ? (π ≃ \(\frac { 22 }{ 7 }\))
(i) 3 ସେ.ମି., 4 ସେ.ମି., 5 ସେ.ମି.
(ii) 8 ସେ.ମି., 6 ସେ.ମି., 1 ସେ.ମି.
(iii) 17 ସେ.ମି., 14 ସେ.ମି., 7 ସେ.ମି.
Solution:
(i)
ତିନୋଟି ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ ଯଥାକ୍ରମେ 3 ସେ.ମି., 4 ସେ.ମି. ଓ 5 ସେ.ମି. ।
ମନେକର ନୂତନ ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ R ସେ.ମି. ।
ଗୋଲକମାନକର ଆୟତନର ସମସି = ନୂତନ ଗୋଲାକାର ଆୟତନ
⇒ \(\frac { 4 }{ 3 }\) π(3)³ + \(\frac { 4 }{ 3 }\) π (4)³ + \(\frac { 4 }{ 3 }\) π (5)³ = \(\frac { 4 }{ 3 }\) πR³
⇒ \(\frac { 4 }{ 3 }\) π 3³ + 4³ + 5³) = \(\frac { 4 }{ 3 }\) πR³
⇒ 27 + 64 + 125 = R³
⇒ R³ = 216 ⇒ R = 6 ସେ.ମି.
∴ ନୂତନ ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ 6 ସେ.ମି. ।

(ii) ତିନୋଟି ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ ଯଥାକ୍ରମେ 8 ସେ.ମି., 6 ସେ.ମି. ଓ 1 ସେ.ମି. ।
ମନେକର ନୂତନ ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ R ସେ.ମି. |
⇒ \(\frac { 4 }{ 3 }\) π(8)³ + \(\frac { 4 }{ 3 }\) π(6)³ + \(\frac { 4 }{ 3 }\) π(1)³ = \(\frac { 4 }{ 3 }\) πR³
⇒ \(\frac { 4 }{ 3 }\) π(8)³ + 6³ + 1)³ = \(\frac { 4 }{ 3 }\) πR³ ⇒ 512 + 216 + 1 = R³
⇒ R³ = 729 ⇒ R = 9 ସେ.ମି.
∴ ନୂତନ ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ 9 ସେ.ମି. |

(iii) ତିନୋଟି ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ ଯଥାକ୍ରମେ 17 ସେ.ମି., 14 ସେ.ମି. ଓ 1 ସେ.ମି. ।
ମନେକର ନୂତନ ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ R ସେ.ମି. ।
ଗୋଲକମାନକର ଆୟତନର ସମସି = ନୂତନ ଗୋଲାକାର ଆୟତନ
⇒ \(\frac { 4 }{ 3 }\) π (17)³ + \(\frac { 4 }{ 3 }\) π (14)³ + \(\frac { 4 }{ 3 }\) π (7)³ = \(\frac { 4 }{ 3 }\) πR³
⇒ 4913 + 2744 + 343 = R³
⇒ R³ = 8000 ⇒ R = 20 ସେ.ମି.
∴ ନୂତନ ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ 20 ସେ.ମି. ।

Question 3.
ନିମ୍ନ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଦୁଇଟି ଲେଖାଏଁ ଗୋଲକର ବ୍ୟାସର ଅନୁପାତ ବା ବ୍ୟାସାର୍ଦ୍ଧର ଅନୁପାତ ଦର ଅଛି । ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଗୋଲକଦ୍ୱୟର ଆୟତନର ଅନୁପାତ ଏବଂ ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ ନିଶ୍ଚୟ କର ।
(i) \(\frac{d_1}{d_2}\) = \(\frac { 3 }{ 4 }\)
(ii) \(\frac{r_1}{r_2}\) = \(\frac { 1 }{ 3 }\)
(iii) \(\frac{r_1}{r_2}\) = \(\frac { 2 }{ 5 }\)
Solution:

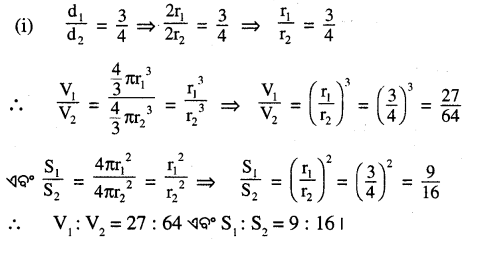
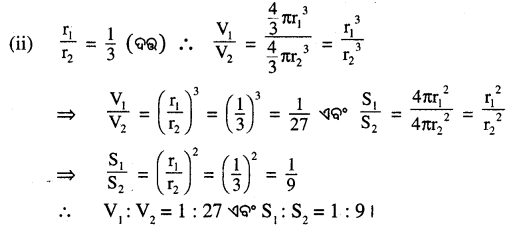
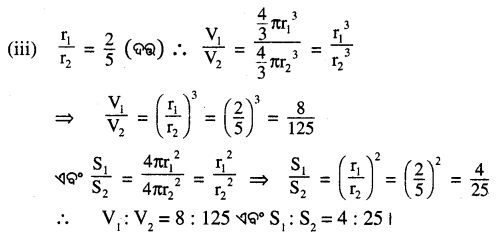
Question 4.
ଗୋଟିଏ ଗୋଲକର ଆୟତନ \(\frac{792}{7}\) ଘନ ସେ.ମି. ହେଲେ ତା’ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ମନେକର ଗୋଲକ ଦ୍ୟାମାଦି r ସେ.ମି. | ∴ ଗୋଲକ ଅନୁପାତ = \(\frac { 4 }{ 3 }\) × \(\frac { 22 }{ 7 }\) r³ = \(\frac { 792 }{ 7 }\)
ପ୍ରଶାନ୍ତପାରେ \(\frac { 4 }{ 3 }\) πr³ = \(\frac { 792 }{ 7 }\) ⇒ \(\frac { 4 }{ 3 }\) × \(\frac { 22 }{ 7 }\) r³ = \(\frac { 792 }{ 7 }\)
⇒ r³ = \(\frac { 792 }{ 7 }\) × \(\frac{7 \times 3}{22 \times 4}\) = 27 ⇒ r = 3 ସେ.ମି.
∴ ଗୋଲକର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 4πr² = 4 × \(\frac { 22 }{ 7 }\) × 3² = \(\frac { 792 }{ 7 }\) = 113\(\frac { 1 }{ 7 }\) = 113 ବ. ସେ.ମି. |

Question 5.
(i) ଗୋଟିଏ ଗୋଲକର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 616 ବ. ସେ.ମି. ହେଲେ ତା’ର ଆୟତନ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
(ii) ଗୋଟିଏ ଗୋଲକର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 5544 ବ. ସେ.ମି. ହେଲେ ତା’ର ବ୍ୟାସାର୍ଦ୍ଧ କେତେ ? (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
(i) ମନେକର ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ r ସେ.ମି. ଓ ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 4πr² ବର୍ଗ ସେ.ମି.
ପ୍ରଶାନ୍ତପାରେ, 4πr² = 616 ⇒ 4 × \(\frac { 22 }{ 7 }\) × r² = 616
⇒ r² = \(\frac{616 \times 7}{4 \times 22}\) = 49 ⇒ r = √49 = 7 ସେ.ମି.
∴ ଆୟତନ = \(\frac { 4 }{ 3 }\) πr³ = \(\frac { 4 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × 7³ = \(\frac { 4312 }{ 3 }\) ବ 1437\(\frac { 1 }{ 3 }\) ପନ. ସେ.ମି. |

(ii) ମନେକର ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ r ସେ.ମି. |
∴ ଏହାର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 4πr² ବର୍ଗ ସେ.ମି.
ପ୍ରଶାନ୍ତପାରେ, 4πr² = 5544 ⇒ 4 × \(\frac { 22 }{ 7 }\) × r² = 5544
⇒ r² = \(\frac{5544 \times 7}{4 \times 22}\) = 441 ⇒ r = √441 = 21 ସେ.ମି.
∴ ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ 21 ସେ.ମି. ।

Question 6.
ଗୋଟିଏ ଗୋଲକର ଘନଫଳ 19404 ଘନ ମିଟର । ଏହାର ସମଘନଫଳବିଶିଷ୍ଟ ଏକ ଅର୍ଦ୍ଧ ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ କେତେ ? (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ଏକ ଗୋଲକର ଘନଫଳ = 19404 ଘନ ମି. = ଅନ୍ୟ ଏକ ଅର୍ଦ୍ଧଗୋଲକର ଘନଫଳ
ମନେକର ଅର୍ଦ୍ଧଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ = r ମି. । ∴ଅର୍ଦ୍ଧଗୋଲକର ଘନଫଳ = \(\frac { 2 }{ 3 }\) πr³ ଘନ ମି.
ପ୍ରଶ୍ନନୁସାରେ, \(\frac { 2 }{ 3 }\) πr³ = 19404 ⇒ \(\frac { 2 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × r³ = 19404
⇒ r³ = 19404 × \(\frac { 7 }{ 22 }\) × \(\frac { 3 }{ 2 }\) = 9261 ⇒ r = \(\sqrt[3]{9261}\) = 21 ମି.
∴ ଅର୍ଦ୍ଧଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ 21 ମି. |

Question 7.
9 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ଧାତବ ଗୋଲକକୁ ତରଳାଇ ସେଥୁ
(i) 1 ସେ.ମି. ବ୍ୟାସାଦ୍ଧ ବିଶିଷ୍ଟ କେତୋଟି କ୍ଷୁଦ୍ର ଗୋଲକ ପ୍ରସ୍ତୁତ କରାଯାଇପାରିବ ? \(\frac { 22 }{ 7 }\)
(ii) 1 ସେ.ମି. ବ୍ୟାସ ବିଶିଷ୍ଟ ବୃତ୍ତାକାର ପ୍ରସ୍ଥଚ୍ଛେଦଥାଇ କେତେ ଲମ୍ବର ତାର ପ୍ରସ୍ତୁତ କରାଯାଇପାରିବ ? \(\frac { 22 }{ 7 }\)
Solution:
(i) 9 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଗୋଲକକୁ ତରଳାଇ = \(\frac { 22 }{ 7 }\) π × 9³ ମି.ସେ.ମି.
1 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ କ୍ଷୁଦ୍ର ଗୋଲକର ଘନଫଳ = \(\frac { 4 }{ 3 }\) π (l)³ = \(\frac { 4 }{ 3 }\) π ପନ. ସେ.ମି.
∴ ଯୁଦ୍ର ଗୋଲକରି ସଂଖ୍ୟା = \(\frac{\frac{4}{3} \pi \times 9^3}{\frac{4}{3} \pi}\) = 9³ = 729

(ii) 9 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଗୋଲକର ଘନପଳ = \(\frac { 4 }{ 3 }\) π × 9³ ମି.ସେ.ମି.
1 ସେ.ମି. ବ୍ୟାସ (ବ୍ୟାସାର୍ଷ = \(\frac { 1 }{ 2 }\) ସେ.ମି.) ଓ h ସେ.ମି. ଲମ୍ବ ବିଶିଷ୍ଟ
ତାରର ଘନଫଳ = π × (\(\frac { 1 }{ 2 }\))² × h ପନ. ସେ.ମି.
ପ୍ରଶାନୁସାରେ, \(\frac { 4 }{ 3 }\) π × 9³ = π × (\(\frac { 1 }{ 2 }\))² × h
⇒ \(\frac { h }{ 4 }\) = \(\frac { 4 }{ 3 }\) × 9³ ⇒ h = \(\frac { 4 }{ 3 }\) × 729 × 4 = 3888 ସେ.ମି.
⇒ h = 38.88 ମିଟର |
∴ 9 ସେ.ମି. ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ଗୋଲକକୁ ତରଳାଇ 1 ସେ.ମି. ବ୍ୟାସ ବିଶିଷ୍ଟ 38.88 ମି. ଲମ୍ବର ତାର ତିଆରି କରାଯାଇପାରିବ ।

Question 8.
ଗୋଟିଏ ଅର୍ଷଗୋଲାକୃତି ପାଣିଟାଙ୍କିର ଭିତର ପାଖର ବ୍ୟାସ 4.2 ମିଟର ହେଲେ ସେଥ‌ିରେ କେତେ ଲିଟର ପାଣି ଧରିବ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ଅର୍ଦ୍ଧ ଗୋଲକର ବ୍ୟାସ = 4.2 ମି.| ଅର୍ଷଗୋଲାକୃତି ବ୍ୟାସାଦି r = 2.1 ମି.|
∴ ଅଦିଗୋଳକର ଆୟତନ = \(\frac { 2 }{ 3 }\)πr³ = \(\frac { 2 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × (2.1)³ = 19.404 ପନ ମିଟର |
∴ପାଣି ଟାଙ୍କିର ଆୟତନ 19.404 ଘନମିଟର |
1 ଶାନମିଟର = 1000 ନଗର |
19.404 ଘନମିଟର = 19.404 × 1000 = 19404 ନଗର
∴ ଅର୍ଦ୍ଧ ଗୋଲାକୃତି ପାଣିଟାଙ୍କିରେ 19404 ଲିଟର ପାଣି ଧରିବ ।

Question 9.
ସମାନ ଭୂମି ବିଶିଷ୍ଟ ଗୋଟିଏ ଅଦ୍ଧଗୋଲକ, ଗୋଟିଏ ସିଲିଣ୍ଡର ଓ ଗୋଟିଏ କୋନ୍‌ର ଆୟତନ ସମାନ ହେଲେ ସେମାନଙ୍କ ଉଚ୍ଚତାର ଅନୁପାତ ସ୍ଥିର କର ।
Solution:
ଅର୍ଦ୍ଧଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ = ଅର୍ଦ୍ଧଗୋଲକର ଉଚ୍ଚତା । ଅର୍ଦ୍ଧଗୋଲକର ଆୟତନ = \(\frac { 2 }{ 3 }\)πr³ ଘନ ଏକକ ।

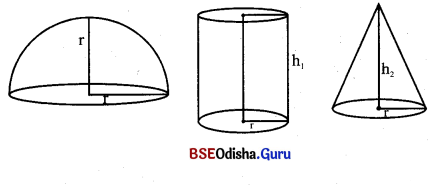
ସିଲିଣ୍ଡରର ଆୟତନ = πr²h₁ ଘନ ଏକକ
କୋନ୍‌ର ଆୟତନ = \(\frac { 1 }{ 3 }\) πr²h₂, ଘନ ଏକକ (h₁ = ସିଲିଣ୍ଡରର ଉଚ୍ଚତା, h₂ = କୋନ୍‌ର ଉଚ୍ଚତା)
∵ ସେମାନଙ୍କର ଆୟତନ ଉଚ୍ଚତା ।
ତେଣୁ \(\frac { 2 }{ 3 }\) πr³ = πr²h₁ = πr²h₁
⇒ \(\frac { 2 }{ 3 }\) r = h₁ = \(\frac { 1 }{ 3 }\) h₂
(∵ ସେମାନଙ୍କର ଭୂମି ସମାନ, ତେଣୁ ସେମାନଙ୍କର ବ୍ୟାସାର୍ଦ୍ଧ ସମାନ ।)
\(\frac{\mathrm{r}}{\mathrm{h}_1}\) = \(\frac { 3 }{ 2 }\) ଏବଂ \(\frac{\mathrm{h}_1}{\mathrm{~h}_2}\) = \(\frac { 2 }{ 6}\)
⇒ r : h₁ : h₂ = 3 : 2 : 6
⇒ ଅର୍ଷଗୋଲକର ଉଚ୍ଚତା : ସିଲିଣ୍ଡରର ଉଚ୍ଚତା : କୋନ୍‌ର ଉଚ୍ଚତା = 3 : 2 : 6

Question 10.
ଗୋଟିଏ ଫମ୍ପା ଧାତବ ଗୋଲକର ଅନ୍ତଃବ୍ୟାସାର୍ଦ୍ଧ 3 ସେ.ମି. ଓ ବହିଃବ୍ୟାସାର୍ଦ୍ଧ 6 ସେ.ମି. । ପ୍ରତି ଘନ ସେ.ମି. ଧାତୁର ବସ୍ତୁତ୍ୱ 8 ଗ୍ରାମ୍ ହେଲେ ତା’ର ବସ୍ତୁତ୍ଵ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ମନେକର ଫମ୍ପା ଗୋଲକର ବହିଃବ୍ୟାସାର୍ଦ୍ଧ R ସେ.ମି. ଏବଂ ଅନ୍ତଃବ୍ୟାସାର୍ଦ୍ଧ r ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, R = 6 ସେ.ମି. ଏବଂ r = 3 ସେ.ମି
ଫମ୍ପା ଧାତବ ଗୋଲକର ଆୟତନ = \(\frac { 4 }{ 3 }\) π (R³ – r³)
= \(\frac { 4 }{ 3 }\) × \(\frac { 22 }{ 7 }\) (6³ – 3³) = \(\frac { 4 }{ 3 }\) × \(\frac { 22 }{ 7 }\) (216 – 27) = \(\frac { 4 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × 189 = 792 ଘନ ସେ.ମି. ।
କିନ୍ତୁ ପ୍ରତି ଘ. ସେ.ମି. ଧାତୁର ବସ୍ତୁତ୍ଵ = 8 ଗ୍ରାମ୍ ।
∴ 792 ଘ. ସେ.ମି. ଧାତୁର ବସ୍ତୁତ୍ଵ = 792 × 8 = 6336 ଗ୍ରାମ୍ ଦା 6.336 କାଣ୍ଡ |

Question 11.
ଗୋଟିଏ ଅର୍ଷଗୋଲକ ଆକୃତିର ପାତ୍ରର ବାହାର ବ୍ୟାସାର୍ଦ୍ଧ 8 ସେ.ମି. ଓ ମୋଟେଇ 1 ସେ.ମି. । ଏହାର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ କେତେ ? (π ≃ √10)
Solution:
ଅର୍ଦ୍ଧଗୋଲକ ଆକୃତି ପାତ୍ରର ବହିଃବ୍ୟାସାର୍ଦ୍ଧ (R) = 8 ସେ.ମି. ଓ ଅନ୍ତଃବ୍ୟାସାର୍ଦ୍ଧ (r) = (8 – 1) = 7 ସେ.ମି.
ଫମ୍ପା ଅର୍ଷଗୋଲକର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πR² + 2πr² + π(R² – r²)
= π(3R² + r²) = √10 (3 × 8² + 7²) = √10 (192 + 49) = 241√10 ଘନ ସେ.ମି. ।

Question 12.
ଗୋଟିଏ ନିଦା ସୀସା। ସମଘନରୁ ଏକ ବୃହତ୍ତମ ଆକାର ବିଶିଷ୍ଟ ଗୋଲକ କାଟି ନିଆଗଲା । ଅବଶିଷ୍ଟ ଅଂଶର ଆୟତନ 12870 ଘନସେ.ମି. ହେଲେ, ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ? (π ≃ 3.14)
Solution:
ମନେକର ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = a ସେ.ମି. ।
ସମଘନର ଆୟତନ = a³ ଘନ ସେ.ମି. ।
ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = ଗୋଲକର ବ୍ୟାସ ।
ଗୋଲକର ବ୍ୟାସାର୍ଦ୍ଧ = \(\frac { a }{ 2 }\) ସେ.ମି.
∴ ଗୋଲକର ଘନଫଳ = \(\frac { 4 }{ 3 }\)π(\(\frac { a }{ 2 }\))³ = \(\frac { 4 }{ 3 }\) × π × \(\frac{a^3}{8}\) ଘନ ସେ.ମି. = \(\frac{\pi \mathrm{a}^3}{6}\) ଘନ ସେ.ମି. |
ପ୍ରଶ୍ନନୁସାରେ, a³ – \(\frac{\pi \mathrm{a}^3}{6}\) = 12870 ⇒ a³(\(\frac{6-\pi}{6}\)) = 12870
⇒ a³ (6 – 3.14) = 12870 × 6 ⇒ a³ × 2.86 = 12870 × 6
⇒ a³ = \(\frac{12870 \times 6}{2.86}\) = 27000 ⇒ a = \(\sqrt[3]{27000}\) = 30 ସେ.ମି. ।
∴ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ 30 ସେ.ମି. ।

Question 13.
ଏକ ଅର୍ଷଗୋଲାକୃତି ବିଶିଷ୍ଟ ପାତ୍ରର ମୋଟେଇ ଓ ବାହାରର ବ୍ୟାସାର୍ଦ୍ଧ ଯଥାକ୍ରମେ 1 ସେ.ମି. ଓ 10 ସେ.ମି. ହେଲେ,
(i) ଏହାର ସମସ୍ତ ପୂର୍ବଭଳର ମୋଟେଇ ନିଣ୍ଡୟ କର ଏବଂ
(ii) ଏଥିରେ ବ୍ୟବହୃତ ଧାତୁର ଆୟତନ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ଅର୍ଦ୍ଧ ଗୋଲାକୃତି ବିଶିଷ୍ଟ ପାତ୍ରର ବହିଃବ୍ୟାସାର୍ଦ୍ଧ (R) = 10 ସେ.ମି.
ଓ ଅନ୍ତଃବ୍ୟାସାର୍ଦ୍ଧ (r) = 10 – 1 = 9 ସେ.ମି.
(i) ଫମା ଅଦିଶଶାଳକର ପମଣ୍ଡ ପୂର୍ବପାଳର ଯେତ୍ରଫଳ = 2πR² + 2πr² + π(R² – r²)
= π (3R² + r²) = π(3 × 10² + 9²) = π (300 + 81) = 381 π ଘନ ସେ.ମି. ।

(ii) ଫମା ଅଦିଶଶାଳକର ଆୟତନ = \(\frac { 2 }{ 3 }\) π (R³ – r³)
= \(\frac { 2 }{ 3 }\) π (10³ – 9³) = \(\frac { 2 }{ 3 }\) π (1000 – 729) = \(\frac { 2 }{ 3 }\) π × 271 = \(\frac{542 \pi}{3}\) ଘନ ସେ.ମି. ।