Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 1 ପୂର୍ଣ୍ଣସଂଖ୍ୟା Ex 1.1 Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Maths Solutions Chapter 1 ପୂର୍ଣ୍ଣସଂଖ୍ୟା Ex 1.1
Question 1.
ନିମ୍ନ ସଂଖ୍ୟାରେଖାରେ ଦର୍ଶାଯାଇଥିବା ପ୍ରକ୍ରିୟା ଓ ତା’ ର ଫଳ ଲେଖ ।
(କ)

ସମାଧାନ:
-5 + 12 = 7
(ଖ)

ସମାଧାନ:
10 + (-17) = -7
Question 2.
ପାର୍ଶ୍ୱସ୍ଥ ମାନଚିତ୍ରରେ ଦର୍ଶାଯାଇଥିବା ବିଭିନ୍ନ ସ୍ଥାନର ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ଦିନର ସର୍ବନିମ୍ନ ତାପମାତ୍ରା ସେଲସିଅସ୍ ଡିଗ୍ରୀରେ ଦିଆଯାଇଛି । ଏହାକୁ ଲକ୍ଷ୍ୟକରି ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।
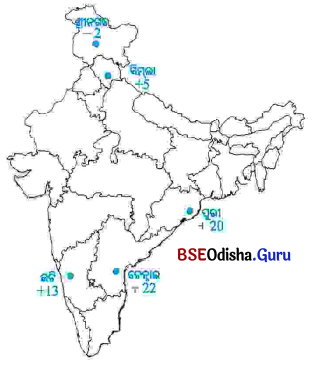
(କ) କେଉଁ ସ୍ଥାନର ତାପମାତ୍ରା ସର୍ବାଧିକ?
ସମାଧାନ:
ଚେନ୍ନାଇର ତାପମାତ୍ରା ସର୍ବାଧ୍ଵ ।
(ଖ) କେଉଁ ସ୍ଥାନର ତାପମାତ୍ରା ସର୍ବନିମ୍ନ?
ସମାଧାନ:
ଶ୍ରୀନଗରର ତାପମାତ୍ରା ସର୍ବନିମ୍ନ ।
(ଗ) କେଉଁ ସ୍ଥାନର ତାପମାତ୍ରା ବେଙ୍ଗାଳୁ ରୁ ର ତାପମାତ୍ରାଠାରୁ ୫ ଡିଗ୍ରୀ କମ୍?
ସମାଧାନ:
ଚିତ୍ରରେ ବେଙ୍ଗାଲୁରର ତାପମାତ୍ରା ଦର୍ଶାଯାଇ ନାହିଁ ।
(ଘ) ଶ୍ରୀନଗର ଓ ଉଟିର ତାପମାତ୍ରା ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ କେତେ?
ସମାଧାନ:
ଶ୍ରୀନଗର ଓ ଉଟିର ତାପମାତ୍ରା ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ 15°C ।
(ଙ) କେଉଁ ଦୁଇଟି ସ୍ଥାନର ତାପମାତ୍ରା ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ 16 ଡିଗ୍ରୀ ?
ସମାଧାନ:
ଚିତ୍ରରେ ବେଙ୍ଗାଲୁରର ତାପମାତ୍ରା ଦର୍ଶାଯାଇ ନାହିଁ ।
![]()
Question 3.
ଗୋଟିଏ ସାଧାରଣ ଜ୍ଞାନ ପ୍ରତିଯୋଗିତାରେ ଗୋଟିଏ ପ୍ରଶ୍ନର ଠିକ୍ ଉତ୍ତର ଲାଗି +1 ନମ୍ବର ଓ ଭୁଲ ଉତ୍ତର ଲାଗି -1 ନମ୍ବର ଦିଆଯାଏ । ପ୍ରତ୍ୟେକ ପ୍ରତିଯୋଗୀକୁ ଚାରୋଟି ପାଳିରେ ପ୍ରଶ୍ନ ପଚରାଯାଏ ଓ ପ୍ରତିପାଳିରେ 25 ଟି ପ୍ରଶ୍ନ ପଚରାଯାଏ ମନିଷାକୁ ଚାରୋଟି ପାଳିରେ ପଚରାଯାଇଥିବା ପ୍ରଶ୍ନ ଲାଗି ସେ ପାଇଥିବା ନମ୍ବରଗୁଡ଼ିକ ହେଲା 7, -3, 5 ଓ -5 । ତେବେ ସେ ମୋଟ କେତେ ନମ୍ବର ପାଇଲା?
ସମାଧାନ:
ମନିଷା ଚାରୋଟି ପାଳିରେ ପାଇଥିବା ନମ୍ବରଗୁଡ଼ିକ ହେଲା : 7, -3, 5 ଓ -5
ମନିଷା ମୋଟ ନମ୍ବର ପାଇଲା = 7 + (-3) + 5 + (-5) = 4
∴ ମନିଷା ମୋଟ 4 ନମ୍ବର ପାଇଲା ।
Question 4.
ଏକ ସମୟରେ ଗୋଟିଏ ଉଡ଼ାଜାହାଜ ସମୁଦ୍ରପତ୍ତନଠାରୁ 5000 ମି. ଉପରେ ଉଡ଼ୁଥିବା ବେଳେ ଏକ ବୁଡ଼ାଜାହାଜ ସମୁଦ୍ର ପତ୍ତନ ଠାରୁ 1500 ମି. ଗଭୀରତାରେ ଗତି କରୁଥିଲା ତେବେ ସେହି ସମୟରେ ଉକ୍ତ ଜାହାଜ ଦୁଇଟି ମଧ୍ୟରେ ଦୂରତା କେତେ?

ସମାଧାନ:
ଏକ ଉଡ଼ାଜାହାଜ ସମୁଦ୍ରପତ୍ତନଠାରୁ 5000 ମି. ଉପରେ ଉଡୁଥିଲା ଏବଂ ସେହି ସମୟରେ ଏକ ଚୁଡ଼ା ଜାହାଜ
ସମୁଦ୍ରପତ୍ତନଠାରୁ 1500 ମି. ଗଭୀରତାରେ ଗତି କରୁଥିଲା ।
ଜାହାଜଦ୍ଵୟ ମଧ୍ଯରେ ଦୂରତା = 5000 ମି. + 1500 ମି. = 6500 ମି.
∴ ସେହି ସମୟରେ ଉକ୍ତ ଜାହାଜ ଦୁଇଟି ମଧ୍ୟରେ ଦୂରତା 6500 ମି.
Question 5.
ଗୋଟିଏ କୁହୁକ ବର୍ଗରେ ଡାହାଣରୁ ବାମକୁ,ଉପରୁ ତଳକୁ ବା ଗୋଟିଏ କଣରୁ ବିପରୀତ କଣକୁ ଥିବା ସଂଖ୍ୟାଗୁଡ଼ିକର ଯୋଗଫଳ ସର୍ବଦା ସମାନ । ଏବେ କହ, ନିମ୍ନରେ ଥିବା ବର୍ଗ ଦୁଇଟି ମଧ୍ୟରୁ କେଉଁଟି ପୂର୍ବ ସମ୍ପର୍କ ଥିବା ଏକ କୁହୁକବର୍ଗ?
| +2 | +8 | 0 |
| -3 | +1 | -4 |
| +4 | -6 | -7 |
| -7 | +4 | -6 |
| -2 | -3 | -4 |
| 0 | -10 | +1 |
ସମାଧାନ:
ପ୍ରଥମ ବର୍ଗରେ 0 + (-8) + (+2) = -6
0 + (-4) + (-7) = -11
0 + (+1) + (+4) = 5
ଏଠାରେ ଯୋଗଫଳଗୁଡ଼ିକ ସମାନ ନୁହେଁ
ଦ୍ବିତୀୟ ବର୍ଗରେ (−6) + (+4) + (-7) = -9,
(-6) + (-4) + (+1) = -9
(-6) + (-3) + 0 = -9
ଏଠାରେ ଯୋଗଫଳଗୁଡ଼ିକ ସମାନ ।
∴ ବର୍ଗଦୁଇଟି ମଧ୍ୟରୁ ଦ୍ବିତୀୟ ବର୍ଗଟି ପୂର୍ବ ସମ୍ପର୍କଥିବା ଏକ କୁହୁକ ବର୍ଗ ।
Question 6.
a ଓ b ଲାଗି ନିମ୍ନସଂଖ୍ୟାମାନ ନେଇ a – (-b) = a + b ଏହାର ସତ୍ୟତା ପରୀକ୍ଷା କର ।
(କ) a = 12, b = 15
ସମାଧାନ:
ବାମପାର୍ଶ୍ୱ = a – (-b) = 12 – (-15) = 12 + 15 = 27
ଦକ୍ଷିଣପାର୍ଶ୍ୱ = a + b = 12 + 15 = 27 ∴ a – (-b) = a + b (ପ୍ରମାଣିତ)
(ଖ) a = 225, b = 321
ସମାଧାନ:
ବାମପାର୍ଶ୍ୱ = a – (-b) = 225 – (-321) = 225 + 321 = 546
ଦକ୍ଷିଣପାର୍ଶ୍ୱ = a + b = 225 + 321 = 546 ∴ a – (-b) = a + b (ପ୍ରମାଣିତ)
(ଗ) a = -8, b = 0
ସମାଧାନ:
ବାମପାର୍ଶ୍ୱ = a- (-b) = (-8) – (-0) = -8
ଦକ୍ଷିଣପାର୍ଶ୍ୱ = a + b = -8 + 0 = -8 ∴ a – (-b) = a + b (ପ୍ରମାଣିତ)
(ଘ) a = -18, b = +16
ସମାଧାନ:
ବାମପାର୍ଶ୍ୱ = a – (-b) = (-18) – (-16) = -18 + 16 = -2
ଦକ୍ଷିଣପାର୍ଶ୍ୱ = a + b = -18 + 16 = -2 ∴ a – (-b) = a + b (ପ୍ରମାଣିତ)
Question 7.
ସରଳ କର :
(କ) +5 + (-7) – (-3)
ସମାଧାନ:
+5 + (-7 )- (-3) = 5 – 7 + 3 = 5 + 3 – 7 = 8 – 7 = 1
(ଖ) -18 + (-3) – 12
ସମାଧାନ:
-18 + (-3) – 12 = -18 – 3 – 12 = -(18 + 3 + 12) = -33
(ଗ) +25 – (+7) + (-18)
ସମାଧାନ:
+25 – (+7) + (-18) = (25 – 7) – 18 = 18 – 18 = 0
(ଘ) -35 – (-20)+ (-14)
ସମାଧାନ:
(-35) – (-20) + (-14) = -35 + 20 – 14 = -15 – 14 = -29
![]()
Question 8.
ଶ୍ୟାମଳୀ ତା’ଘର ପାଖରୁ 25 ମିଟର ପୂର୍ବକୁ ଗଲାପରେ ପହଞ୍ଚିବା ସ୍ଥାନରୁ 27 ମିଟର ପଶ୍ଚିମକୁ ଫେରିଲା । ତେବେ ସେ ତା’ ଘର ପାଖରୁ କେଉଁ ଦିଗରେ ଓ କେତେ ଦୂରରେ ପହଞ୍ଚିଲା?

ସମାଧାନ:
ଶ୍ୟାମଳୀ ତା’ ଘର ପାଖରୁ ପୂର୍ବକୁ ଗଲା = 25 ମିଟର
ଓ ପହଞ୍ଚିବା ସ୍ଥାନରୁ ପଶ୍ଚିମକୁ ଫେରିଲା = 27 ମିଟର
ପୂର୍ବକୁ 25 ମି. + ପଶ୍ଚିମକୁ 27 ମି. = 25 ମି. + (-27 ମି.) ପୂର୍ବକୁ
= (25 – 27) ମି ପୂର୍ବକୁ = –2 ମି ପୂର୍ବକୁ ଅର୍ଥାତ୍ ପଶ୍ଚିମକୁ 2 ମିଟର ।
∴ ଶ୍ୟାମଳୀ ତା’ ଘର ପାଖରୁ ପଶ୍ଚିମ ଦିଗରେ ଓ 2 ମିଟର ଦୂରରେ ପହଞ୍ଚିଲା ।
Question 9.
(କ) ଯୋଗଫଳ କେତେ ହେବ ସ୍ଥିର କର ।
-8 + 7 – 6 + 5 – 4 + 3 – 2 + 1
ସମାଧାନ:
-8 + 7 – 6 + 5 – 4 + 3 – 2 + 1 = (7 + 5 + 3 + 1) – (8 + 6 + 4 + 2)
= 16 – 20 = – 4
(ଖ) ସଂଖ୍ୟାଗୁଡ଼ିକୁ ପ୍ରଥମରୁ ଯୋଡ଼ି ଯୋଡ଼ି କରି ନେଇ ତା’ପରେ ଯୋଗଫଳ କେତେ ସ୍ଥିର କର ।
ସମାଧାନ:
-8 + 7 – 6 + 5 – 4 + 3 – 2 + 1
= (-8 + 7) + (-6 + 5) + (-4 + 3) + (-2 + 1) = -1 – 1 – 1 – 1 = -4
(ଗ) ଯୋଗଫଳ ସ୍ଥିର କର ।
(-4) + (-3) + (-2) + (-1) + 0 + (+1) + (+2) + (+3) + (+4)
ସମାଧାନ:
(-4) + (-3) + (-2) + (-1) + 0 + (+1) + (+2) + (+3) + (+4)
= (-4 + 4) + (-3 + 3) + (-2 + 2) + (-1 + 1) + 0
= 0 + 0 + 0 + 0 + 0 = 0
