BSE Odisha 8th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(b)

Odisha State Board BSE Odisha 8th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(b) Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(b)

Question 1.
ପମଦିବ।ତୁ ତିଭୁଲରେ
(i) ଭୂମିର ଦୈର୍ଘ୍ୟ 10 ସେ.ମି. ଓ ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ 13 ସେ.ମି. ହେଲେ, ଉଚ୍ଚତା କେତେ ?
(ii) ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ 41 ସେ.ମି. ଏବଂ ଉଚ୍ଚତା ୨ ସେ.ମି. ହେଲେ, ଭୂମିର ଦୈର୍ଘ୍ୟ କେତେ ?
(iii) ଭୂମିର ଦୈର୍ଘ୍ୟ 14 ସେ.ମି. ଏବଂ ଉଚ୍ଚତା 24 ସେ.ମି. ହେଲେ, ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ?
(iv) ଉଚ୍ଚତା 12 ସେ.ମି. ଓ ଭୂମିର ଦୈର୍ଘ୍ୟ ଉଚ୍ଚତାଠାରୁ 2 ସେ.ମି. କମ୍ ହେଲେ, ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ?
Solution:
(i) ABC ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ 13 ସେ.ମି. ଓ ଭୂମିର ଦୈର୍ଘ୍ୟ 10 ସେ.ମି. ।

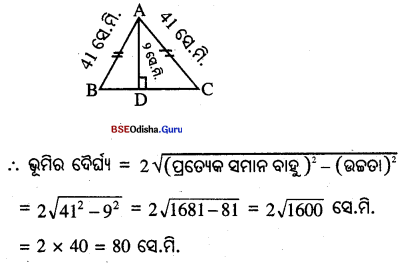
(ii) ABC ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ 41 ସେ.ମି. ଓ ଭୂମିର 9 ସେ.ମି. ।

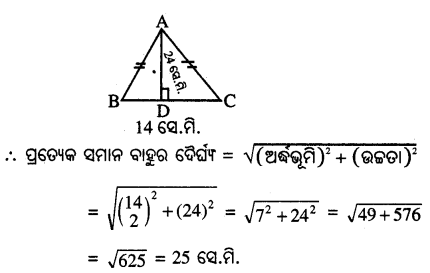
(iii) ABC ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ 12 ସେ.ମି. ଓ ଭୂମିର 24 ସେ.ମି. ।

(iv) ABC ସମଡ଼ିବାହୁ ତ୍ରିଭୁଜର ଉଚ୍ଚତାର ଦୈର୍ଘ୍ୟ 12 ସେ.ମି. ଓ ଭୂମିର ଦୈର୍ଘ୍ୟ ଉଚ୍ଚତାର ଦୈର୍ଘ୍ୟଠାରୁ 2 ସେ.ମି. କମ୍।
ଦୈର୍ଘ୍ୟ ଉଚ୍ଚତାର ଦୈର୍ଘ୍ୟଠାରୁ = 12 – 2 = 10 ସେ.ମି. କମ୍।

Question 2.
ABC ସମକୋଣା ପ୍ରଭୁକରେ m∠B = 90° ଓ AB = AC
(i) AB = 8 ସେ.ମି., କଣ୍ଠ \(\overline{\mathrm{AC}})\) ର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
(ii) AB = 7 ସେ.ମି. ହେଲେ, କଅଁ AC ର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
(iii) କଣ୍ଠ A ର ଦୈର୍ଘ୍ୟ 40 ସେ.ମି. ହେଲେ, \(\overline{\mathrm{BC}})\) ର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
(iv) କଣ୍ଠ \(\overline{\mathrm{AC}})\) ର ଦୈର୍ଘ୍ୟ 25 ସେ.ମି. ହେଲେ, \(\overline{\mathrm{AB}})\) ର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ABC ସମକୋଣୀ ତ୍ରିଭୁଜର
m∠B = 90° ଓ AB = BC
∴ ABC ଏକ ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।

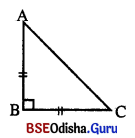
(i) AB = 8 ସେ.ମି. (ବର)
∴ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର କର୍ଷ (AC) ର ଦୈର୍ଘ୍ୟ
= ସମାନ ବାହୁ × √2 = AB × √2
= 8 × 2 = 8√2 ସେ.ମି.
ବିକଳ୍ପ ସମାଧାନ : AC² = AB² + BC² ⇒ AC² = 8² + 8²
⇒ AC² = 2 × 8² ⇒ AC = 8√2 ସେ.ମି.,

(ii) AB = 7 ସେ.ମି. (ବର)
ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର କଣ୍ଠ = √2 × ସମାନ ବାହୁ = 7√2 ସେ.ମି.
∴ AC = 7√2 ସେ.ମି.

(iii) କଣ୍ଠ (AC) = 40 ସେ.ମି. (ଦତ୍ତ)
ଗମଲୋଗ ସମବିବାହି ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେଲ ପାଦନ ଦବାନ୍ତୁର ଦୈର୍ଘ୍ୟ = \(\frac { କଣ୍ଠର ଦୈର୍ଘ୍ୟ }{ 2 }\)
⇒ BC = \(\frac{\mathrm{AC}}{\sqrt{2}}\) = \(\frac{\mathrm{40}}{\sqrt{2}}\) = \(\frac{40 \sqrt{2}}{\sqrt{2} \times \sqrt{2}}\) = \(\frac{40 \sqrt{2}}{2}\) = 20√2
∴BC = 20√2 ସେ.ମି.
ବିକଳ୍ପ ସମାଧାନ : AC² = AB² + BC² = BC² + BC² (∵ AB = BC)
⇒ 40² = 2 BC² ⇒ √2BC = 40
⇒ AB = \(\frac{\mathrm{40}}{\sqrt{2}}\) = 20√2 ସେ.ମି.

(iv) କର୍ଷ (AC) = 25 ସେ.ମି. (ଦ୍‌ର)
ସମକୋଣୀ ସମଙ୍ଗିବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac { କଣ୍ଠର ଦୈର୍ଘ୍ୟ }{ 2 }\)
\(\frac{25}{\sqrt{2}}\) = \(\frac{25 \sqrt{2}}{2}\) = 12.5√2 ସେ.ମି. |
∴AB = 12.5√2 ସେ.ମି. |

Question 3.
(i) ଗୋଟିଏ ବର୍ଗଚିତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ 7 ସେ.ମି. ହେଲେ, କର୍ପୂର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
(ii) ଗୋଟିଏ ବର୍ଗଚିତ୍ରର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 18 ସେ.ମି. ହେଲେ, ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
(iii) ଗୋଟିଏ ବର୍ଗଚିତ୍ରର କଣ୍ଠର ଦୈର୍ଘ୍ୟ 22√2 ସେ.ମି. ହେଲେ, ଏହାର ପରିସୀମା ନିର୍ଣ୍ଣୟ କର ।
(iv) ଗୋଟିଏ ବର୍ଗଚିତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ 2 ସେ.ମି. ବର୍ଗଚିତ୍ରର କଣ୍ଠ କେତେ ସେ.ମି. ବଢ଼ିବ ?
Solution:
(i) ଏକ ବର୍ଗଚିତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = 7 ସେ.ମି.
∴ ବର୍ଗଚିତ୍ରର କର୍ପୂର ଦୈର୍ଘ୍ୟ = ବାହୁର ଦୈର୍ଘ୍ୟ × √2 = 7 × √2 = 7√2 ସେ.ମି.

(ii) ଏକ ବର୍ଗଚିତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = 18 ସେ.ମି.
∴ ବର୍ଗଚିତ୍ରର କର୍ପୂର ଦୈର୍ଘ୍ୟ = \(\frac { କଣ୍ଠର ଦୈର୍ଘ୍ୟ }{ 2 }\) = \(\frac{18}{\sqrt{2}}\) = \(\frac{18 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}\) = \(\frac{18 \sqrt{2}}{2}\) = 9√2 ସେ.ମି.

(iii) ବର୍ଗଚିତ୍ରର କଣ୍ଠର ଦୈର୍ଘ୍ୟ = 22√2 ସେ.ମି.
∴ ବର୍ଗଚିତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac { କଣ୍ଠର ଦୈର୍ଘ୍ୟ }{ 2 }\) = \(\frac{22 \sqrt{2}}{\sqrt{2}}\) = 22 ସେ.ମି.
ପରିସୀମା = ବାହ୍ନ × 4 = 22 × 4 = 88 ସେ.ମି. |

(iv) ମନେକର ବାହୁର ଦୈର୍ଘ୍ୟ a ସେ.ମି. ଓ କର୍ଣ୍ଣ = √2 a ସେ.ମି. |
2 ସେ.ମି. ବଢ଼ିଗଲେ ବାହୁର ଦୈର୍ଘ୍ୟ = (a + 2) ସେ.ମି. ଓ କର୍ପୂର ଦୈର୍ଘ୍ୟ = √2(a + 2) ସେ.ମି. |
ଅଧ୍ଵଜ = √2(a + 2) – √2a = √2a + 2√2 – √2a = 2√2 ସେ.ମି.
∴ ବାହୁର ଦୈର୍ଘ୍ୟ 2 ସେ.ମି. ବଢ଼ିଲେ କର୍ପୂର ଦୈର୍ଘ୍ୟ 2√2 ସେ.ମି. ବଢ଼ିବ ।

Question 4.
ଗୋଟିଏ ଆୟତଚିତ୍ରର ସମକୋଣସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିମ୍ନରେ ଦତ୍ତ ଅଛି । କର୍ପୂର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
(i) 75 ମି. ଓ 40 ମି.
(ii) 14 ମି. ଓ 48 ମି.
Solution:
(i) ଆୟତଚିତ୍ରର ସମକୋଣସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 75ମି. ଓ 40 ମି. ।
∴ଏହାର କର୍ପୂର ଦୈର୍ଘ୍ୟ
= \(\sqrt{75^2+40^2}\) = \(\sqrt{5^2 \times 15^2+5^2 \times 8^2}\) = \(\sqrt{5^2 \times\left(15^2+8^2\right)}\) = \(\sqrt{5^2 \times 17^2}\) ( ∵ 8, 15, 17 ଏକ ପିଥାଗୋରୀୟ ଟ୍ରିପଲ୍)
= 5 × 17 = 85 ମି. ।

(ii) ଆୟତଚିତ୍ରର ସମକୋଣସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 14ମି. ଓ 48 ମି. ।
∴ଏହାର କର୍ପୂର ଦୈର୍ଘ୍ୟ
= \(\sqrt{14^2+48^2}\) = \(\sqrt{2^2 \times 7^2+2^2 \times 24^2}\) = \(\sqrt{2^2\left(7^2+24^2\right)}\) = \(\sqrt{2^2 \times 25^2}\) (∵ 7, 24 ଓ 25 ଏକ ପିଥାଗୋରୀୟ ଟ୍ରିପଲ୍)
= 2 × 25 = 50 ମି. ।

Question 5.
ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜର ପରିସୀମା 24 ସେ.ମି. ହେଲେ, ଏହାର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
ସମବାହୁ △ ର ପରିସୀମା = 24 ସେ.ମି. ।
ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac { ପରିସୀମା }{ 3 }\)
∴ ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac { 24 }{ 3 }\) = 8 ସେ.ମି.
ଉଚ୍ଚତା = \(\frac{\sqrt{3}}{2}\) × ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac{\sqrt{3}}{2}\) × 8 = 4√3 ସେ.ମି.
∴ ସମବାହୁ △ ର ଉଚ୍ଚତା 4√3 ସେ.ମି. ।

Question 6.
ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜର ଏକ ଶୀର୍ଷବିନ୍ଦୁରୁ ବିପରୀତ ବାହୁର ମଧ୍ୟବିନ୍ଦୁର ଦୂରତା 15√3 ଡେସିମିଟର ହେଲେ, ଏହାର ପରିସୀମା ନିର୍ଣ୍ଣୟ କର ।
Solution:
ସମବାହୁ ତ୍ରିଭୁଜର ଏକ ଶୀର୍ଷବିନ୍ଦୁରୁ ବିପରୀତ ବାହୁର ମଧ୍ୟବିନ୍ଦୁର ଦୂରତା
= ସମବାହୁ ତ୍ରିଭୁଜର ଉଚ୍ଚତା = 15√3 ଡେସି ମି.
ସମବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ମପାନ ବାହୁର ଦୈର୍ଘ୍ୟ = ଉଚ୍ଚତା × \(\frac{2}{\sqrt{3}}\) = 15√3 × \(\frac{2}{\sqrt{3}}\) = 30 ଡେସି ମି.
∴ ସମବାହୁ ତ୍ରିଭୁଜର ପରିସୀମା = ବାହୁର ଦୈର୍ଘ୍ୟ × 3 = 30 ହେକିମି. × 3 = 90 ଡେସି ମି. |

Question 7.
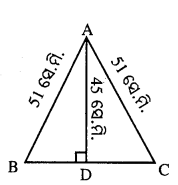
ଗୋଟିଏ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ସମାନ ବାହୁ 51 ସେ.ମି. ଓ ତୃତୀୟ ବାହୁ ପ୍ରତି ଅଙ୍କିତ ଉଚ୍ଚତାର ଦୈର୍ଘ୍ୟ 45 ସେ.ମି. ହେଲେ, ଏହି ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
AB = AC = 51 ସେ.ମି. , AD = 45 ସେ.ମି.
∴ BD (ଅର୍ଦ୍ଧଭୂମି)
= \(\sqrt{A B^2-A D^2}\) = \(\sqrt{51^2-45^2}\) = \(\sqrt{3^2 \cdot 17^2-3^2 \cdot 15^2}\) = \(\sqrt{3^2\left(17^2-15^2\right)}\) = \(\sqrt{3^2 \cdot 8^2}\) = 3 × 8 = 24 ସେ.ମି.
∴ BC = 2BD = 2 × 24 = 48 ସେ.ମି.
∴ ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ 48 ସେ.ମି. |

Question 8.
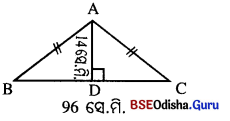
ଗୋଟିଏ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ 96 ସେ.ମି. ଓ ଉଚ୍ଚତା 14 ସେ.ମି. ଦ୍ରେଲେ, ଏହାର ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ ଓ ପରିସୀମା ନିର୍ଣ୍ଣୟ କର ।
Solution:
ABC ସମଦ୍ବିବାହୁ △ ର BC = ଭୂମି = 6 ସେ.ମି.
∴BD = 1/2 BC = 1/2 × 96 = 48 ସେ.ମି.
AD = ଉଚ୍ଚତା = 14 ସେ.ମି. AB ଓ AC ତ୍ରିଭୁଜର ସମାନ ବାହୁ ।
ABD ସମରୋଗ ତ୍ରିଭୁଜର ∠D ପପକୋଶୀ | AB = କଣ୍ଡ, AD = ଭଲତା BD = ଭୁମି ପିଆରେ।ଉପକ ଉପପାଦ୍ୟ ଅନୁସାରେ,
∴ AB = \(\sqrt{\mathrm{AD}^2+\mathrm{BD}^2}\) = \(\sqrt{14^2+48^2}\) = \(\sqrt{2^2 \cdot 7^2+2^2 \cdot 24^2} \) = \(\sqrt{2^2\left(7^2+24^2\right)}\) = \(\sqrt{2^2 \cdot 25^2}\) = 2 × 25 = 50 ସେ.ମି. | ( ∵57, 24, 25 ଏକ ପିଆରେ।ଦାପ ବାହୁର )
∴ ପରିମାପ। = 96 + 50 + 50 = 196 ସେ.ମି. |
∴ ସମଙ୍ଗିବାହୁ △ ର ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ 50 ସେ.ମି. ଓ ପରିସୀମା 196 ସେ.ମି. ।

Question 9.
ଗୋଟିଏ ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ପରିସୀମା 8(√2 + 1) ମିଟର ହେଲେ, ଏହାର ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ପରିସୀମା = 8(√2 + 1) ମିଟର |
ମନେକର ସମକୋଣୀ ସମଦିବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ସମାନ୍ ବାହୁ = a ମିଟର
ତେବେ କାଣ୍ଡର ଦେଶ୍ୟ = √2a ମି. |
∴ △ ର ପରିସୀମା = a + a + √2.a = 2a + √2.a = √2a (√2 + 1) ମି.
ପ୍ରଶ୍ନନୁସାରେ √2.a (√2 + 1) = 8 ( √2 + 1)
⇒ √2.a = 8 ⇒ a = \(\frac{8}{\sqrt{2}}\) = \(\frac{8 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}\) = \(\frac{8 \sqrt{2}}{2}\) = 4√2 ମି.
∴ ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ସମାନ୍ କାଣ୍ଡର ଦେଶ୍ୟ 4√2 ମି.

Question 10.
ଗୋଟିଏ ବର୍ଗଚିତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ 5 ସେ.ମି. ବଢ଼ିଗଲେ ଏହାର ପରିସୀମାରେ କେତେ ବୃଦ୍ଧି ଘଟିବ ଏବଂ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟରେ ମଧ୍ୟ କେତେ ବୃଦ୍ଧି ଘଟିବ ସ୍ଥିର କର ।
Solution:
ମନେକର ବର୍ଗଚିତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ a ସେ.ମି.
∴କଣ୍ଠ = √2 a ସେ.ମି. ଓ ପରିସୀମା = 4a ସେ.ମି.
ବାହୁ 5 ସେ.ମି. ବଢ଼ିଲେ ବାହୁର ଦୈର୍ଘ୍ୟ = (a + 5) ସେ.ମି.
କଣ୍ଠର ଦୈର୍ଘ୍ୟ = √2(a + 5) ସେ.ମି. ହେବା
ଓ ପରିସୀମା = 4(a + 5) ସେ.ମି.
ପରିସୀମା ବୃଦ୍ଧି ହେବ = 4(a + 5) – 4a = 4a + 20 – 4a = 20 ସେ.ମି.
କଣ୍ଠର ଦୈର୍ଘ୍ୟ ବୃଦ୍ଧି ହେବ = √2(a + 5) – √2a = √2a + 5√2 – √2a = 5√2 ସେ.ମି. ବୃଦ୍ଧି ଘଟିବ |