CHSE Odisha Class 11 Math Solutions Chapter 3 Relations And Function Ex 3(c)

Odisha State Board CHSE Odisha Class 11 Math Solutions Chapter 3 Relations And Functions Ex 3(c) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 3 Relations And Functions Exercise 3(c)

Question 1.
Give an example of a relation that is not a function.
Solution:
Let the relation ‘f’ be defined from
A = {1, 2, 3} to B = {1, 2} as
f = {(1, 1), (1, 2), (2, 1), (3, 2)}
f is not a function because f (1) = 1,
f(1) = 2 but 1 ± 2 i.e. f is one many.

Question 2.
If X and Y are sets containing m and n elements respectively then what is the total number of functions from X to Y?
Solution:
If |X| = m and |Y| = n then the number of functions from X to Y = |Y|^|X| = n^m

Question 3.
Find the domain of the following functions:
(i)\( \sqrt{9-x^2}\)
Solution:
y = f(x) = \(\sqrt{9-x^2}\)
Clearly, f(x) is well-defined for 9 – x² ≥ 0 ⇒ x² ≤ 3² ⇒ – 3 ≤ x ≤ 3
∴ dom f = [ – 3, 3]

(ii) \(\frac{x}{1+x}\)
Solution:
y = f(x) = \(\frac{x}{1+x}\)
f(x) is well defined for all x ∈ R
∴ dom f = R

(iii) 1 – |x|
Solution:
y = f(x) = 1 – |x|
f(x) is well defined for all x ∈ R
∴ dom f = R

(iv) \(\frac{1}{x^2-1}\)
Solution:
y = f(x) = \(\frac{1}{x^2-1}\)
f(x) is well defined for x² – 1 ≠ 0
⇒ x² ≠ 1
⇒ x² ≠ ± 1
∴ dom f = R – { -1, 1}

(v) \(\frac{\sin x}{1+\tan x}\)
Solution:
y – f(x) = \(\frac{\sin x}{1+\tan x}\)
f(x) is well defined for 1 + tan x
≠ 0
⇒ tan x ≠ – 1
⇒ x ≠ n π + \(\frac{3 \pi}{4}\)
∴ dom f = R – {n π + \(\frac{3 \pi}{4}\)}

(vi) \(\frac{x}{|x|}\)
Solution:
y = f(x) = \(\frac{x}{|x|}\)
f(x) is well defined for |x| ≠ 0
⇒ x ≠ 0
∴ dom f = R – {0}

(vii) \(\frac{1}{x+|x|}\)
Solution:
y = f(x) = \(\frac{1}{x+|x|}\)
f(x) is well-defined for
x + |x| ≠ 0
⇒ |x| ≠ – x
⇒ x is not negative
⇒ dom f = [0, – ∞)

(viii) \(\sqrt{\log \left(\frac{12}{x^2-x}\right)}\)
Solution:
y = f(x) = \(\sqrt{\log \left(\frac{12}{x^2-x}\right)}\)
f(x) is well defined for \(\frac{12}{x^2-x}\) ≥ 1
⇒ 12 ≥ x² – x
⇒ x² – x – 12 ≤ 0
⇒ (x – 4) (x + 3) ≤ 0
Let us draw the signing scheme

⇒ x ∈ [ – 3, 4]
∴ dom f =[-3, 4]

(ix) [x] – x
Solution:
y = f(x) = [x] – x
f(x) is well defined for all x ∈ R
∴ dom f = R

(x) \(\frac{1}{\sqrt{1-x^2}}\)
Solution:
y = f(x) = \(\frac{1}{\sqrt{1-x^2}}\)
f(x) is well defined for 1 – x² > 0
⇒ x² < 1 ⇒ – 1 < x < 1
∴ dom f = (-1, 1)

(xi) log (sin x)
Solution:
y = f(x) = log (sin x)
fix) is well-defined for sin x > 0
⇒ x ∈ (2nπ , (2n + l)π), n ∈ Z

Question 4.
Find the range of the following functions:
(i) \(\frac{x^2-1}{x^2+1}\)
Solution:
Let y = f(x) = \(\frac{x^2-1}{x^2+1}\)
⇒ x² – y + y = x² – 1
⇒  x²y – x² = – (1 + y)
⇒ x² (y- 1)=-(1 + y)
⇒ x² = \(\frac{\ – (1+y)}{y-1}=\frac{1+y}{1-y}\)
⇒ x = ± \(\sqrt{\frac{1+y}{1-y}}\)
Now x is well-defined for
\(\frac{1+y}{1-y}\) ≥ 0

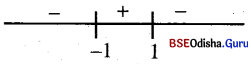
∴ rng f = [-1,1)

(ii) \(\sqrt{x-1}\)
Solution:
y = f(x) = \(\sqrt{x-1}\)
⇒ y² = x- 1
⇒ x = y² + 1
x is well difierid for all y ∈ R but
y ≥ 0
∴ rng f = [0, ∞]

(iii) [x] – x
Solution:
y = f(x) = [x], – x
We have [x] ≤ x < [ x] + 1
⇒ 0 ≤ x – [x] < 1
⇒ 0 ≥ [x] – x > – 1
⇒ -1 < [x] – x ≤ 0
⇒ -1 < y ≤ 0
⇒ rng f = ( – 1 , 0]

(iv) \(\frac{x}{1-x}\)
Solution:
y = f(x) = \(\frac{x}{1-x}\)
⇒ y – xy = x
⇒ xy + x = y
⇒ x (y + 1) = y
⇒ x = \(\frac{y}{y+1}\)
x is well defined for y ≠ – 1
∴ Rng f = R – {- 1}

(v) \(\frac{x}{1+x^2}\)
Solution:
y = f(x) = \(\frac{x}{1+x^2}\)
⇒ y + x²y = x
⇒ x²y – x + y = 0
⇒ x = \(\frac{1 \pm \sqrt{1-4 y^2}}{2 y}\)
x is well defined for 1 – 4y² ≥ 0 and y ≠ 0
⇒ y² ≤ \(\frac{1}{4}\) and y ≠ 0
⇒ – \(\frac{1}{2}\) ≤ y ≤ \(\frac{1}{2}\) and y ≠ 0
but for x = 0 we have y = 0
∴ rng f = \(\left[-\frac{1}{2}, \frac{1}{2}\right]\)

(vi) \(\frac{1}{2-\cos 3 x}\)
Solution:
y = f(x) = \(\frac{1}{2-\cos 3 x}\)
we have – 1 ≤ cos 3x ≤ 1
⇒ 1 ≥ – cos 3x ≥ -1
⇒ – 1 ≤- cos 3x ≤ 1
⇒ 2 – 1 < 2 – cos 3x ≤ 3
⇒ 1 ≤ 2 – cos 3x ≤ 3
⇒ 1 ≥ \(\frac{1}{2-\cos 3 x} \geq \frac{1}{3}\)
⇒ \(\frac{1}{3}\) ≤ y ≤ 1
∴ rng f =[\(\frac{1}{3}\), 1]

(vii) log ₁₀ (1 – x)
Solution:
y = f(x) = log₁₀ (1 – x)
Clearly y ∈ R
∴ rng f = R

(viii) \(\sqrt{1+x^2}\)
Solution:
y = f(x) = \(\sqrt{1+x^2}\)
⇒ y² = 1 + x²
⇒  x² = y² – 1
⇒ x = ± \(\sqrt{y^2-1}\)
x is well defined for y² – 1 ≥ 0
⇒ y² ≥ 1
⇒ – 1 ≥ y ≥ 1
But y > 0
∴ rng f = [1, ∞)

Question 5.
Find the domain and range of the following functions:
(i) \(\frac{x^2}{1+x^2}\)
Solution:
y = f(x) = \(\frac{x^2}{1+x^2}\)
Domain:
f(x) is well defined for all x ∈ R
∴ dom f = R
Range (Method – 1):
y = \(\frac{x^2}{1+x^2}\)
⇒ y + yx² = x²
⇒ x² – yx² = y
⇒ x² (1 – y) = y
⇒ x² = \(\frac{y}{1-y}\)
⇒ x = ± \(\sqrt{\frac{y}{1-y}}\)
x is well-defined for \(\frac{y}{1-y}\) ≥ 0

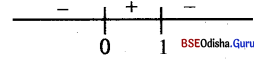
⇒ y 6 [0. 1)
∴ Rng f = [0,1)
Method – 2:
0 ≤ x² < x² + 1
⇒ 0 ≤ \(\frac{x^2}{x^2+1}\) < 1
⇒ 0 ≤ y ≤ 1
∴ rng f = [0, 1)

(ii) \(\sqrt{2 x-3}\)
Solution:
y = f(x) = \(\sqrt{2 x-3}\)
Domain:
f(x) is well defined for 2x- 3 ≥ 0
⇒ x ≥ 3/2
∴ dom f =[\(\frac{3}{2}\), ∞]
Range:
y = \(\sqrt{2 x-3}\) ⇒ y² = 2x – 3
⇒ 2x = y² + 3
⇒ x = \(\frac{y^2+3}{2}\)
x is well defined for all y ∈ R
But y is not negative.
∴ Rng f = [0, ∞)

(iii) log_e |x – 2|
Solution:
y = f(x) = log |x – 2|
Domain:
f(x) is well defined for |x – 2| >0
⇒ x ≠ 2
∴ dom f = R – {2}
Range:
y = log |x – 2| ∈ R ⇒ rng f = R

Question 6.
Give an example of a step function on [- 1, 3] = {x ∈ R| – 1 ≤ x ≤ 3}.
Solution:
f(x) = \(\left\{\begin{array}{c}
-1,-1 \leq x<0 \\
0,0 \leq x<1 \\
1,1 \leq x<2 \\
2,2 \leq x<3 \\
3,3 \leq x<4
\end{array}\right\}\)

Question 7.
Let X ={ a, b, c}, Y = {1, 2, 3, 4}
(a) Find out which of the following relations are functions and which are not and why?
Solution:
X = [a, b, c}, Y = {1, 2, 3, 4}
(i) {(a, 1), (a, 2), (b, 3), (b, 4)}
Solution:
{(a, 1), (a, 2), (b, 3), (b, 4)} is not a function as ‘a’ has two images in Y.

(ii) {(a, 2), (b, 3), (c, 4)}
Solution:
{(a, 2), (b, 3), (c, 4)} is a function from X to Y as the elements of X has unique images in Y.

(iii) {(a, 3), (b, 1), (a, 4), (c, 2)}
Solution:
{(a, 3), (b, 1), (a, 4), (c, 2)} is not a function as ‘a’ and ‘b’ have two images also domain of the function ≠ X.

(iv) {(a, 1), (b, 1), (c, 1)}
Solution:
{(a, 1), (b, 1), (c, 1)} is a function from X to Y.

(v) {(a, 2), (b. 1), (c, 1)}
Solution:
{(a, 2), (b, 1), (c, 1)} is a function from X to Y.

(vi) {(a, a), (b, b), (c, c)}
Solution:
{(a, a), (b, b), (c, c)} is a function from X to X.

(b) Find the domain and range of those relations in a which are functions.
Solution:
(i) The domain of each function is
X = [a, b, c}
Range of functions

(ii) is {2, 3, 4}.
In (iv) is {1} and in (v) is {1, 2}. The range of function in (vi) is X.

(c) Identify the constant function if any.
Solution:
The function in (iv)
i.e. {(a, 1), ib, 1), (c, 1)} is a constant function.

(d) Identify the identity function if any.
Solution:
The function in (vi)
i.e.{(a, a), (b, b), (c, c)} is an identity function.

Question 8.
Find \(f(\sqrt{2})\) and \(\boldsymbol{f}(-\sqrt{3})\) for the function
\(f(x)=\left\{\begin{array}{l}
x^2, \text { if } x<0 \\
x, \text { if } 0 \leq x \leq 1 \\
\frac{1}{x}, \text { if } x>1
\end{array}\right.\)
Solution:
\(f(\sqrt{2})\) = \(\frac{1}{\sqrt{2}}\)
\(\boldsymbol{f}(-\sqrt{3})\) = (√3)² = 3

Question 9.
Find x for which the value of f(x) = x² – 4x + 3 is
Solution:
f(x) = x² – 4x + 3
(i) 0
Solution:
f(x) = 0
⇒ x² – 4x + 3 = 0
⇒ (x – 3) (x – 1) = 0
⇒ x =1, 3

(ii) – 1
Solution:
f(x) = – 1
⇒ x² – 4x + 3 = -1
⇒ x² – 4x + 4 = 0
⇒ (x – 2)² = 0
⇒ x = 2

Question 10.
Find the values of x for which the following functions are not defined:
(i) \(\frac{x^2-4}{x-2}\)
Solution:
y = f(x) = \( \frac{x^2-4}{x-2}\)
Clearly f(x) is not defined for x = 2

(ii) \(\frac{\sin x}{x}\)
Solution:
y = f(x) = \(\frac{\sin x}{x}\)
f(x) is not defined for x = 0

(iii) \(\frac{\log \cos x}{\sec x}\)
Solution:
y = f(x) = \(\frac{\log \cos x}{\sec x}\)
f(x) is not defined for cos x ≤ 0
⇒ for x ∈ x \(\left[\frac{\pi}{2}, \frac{3 \pi}{2}\right]\) or \(\left[\frac{5 \pi}{2}, \frac{7 \pi}{2}\right]\)
In general x ∈ \(\left[(4 n+1) \frac{\pi}{2},(4 n+3) \frac{\pi}{2}\right]\), n ∈ Z

Question 11.
Let f(x) = \(\sqrt{1+x}\), g(x) = \(\sqrt{1-x}\)
Find & Also, find the domain in each case.
Solution:
f(x) = \(\sqrt{1+x}\), g(x) = \(\sqrt{1-x}\)
f(x) is well defined for x + 1 ≥ 0
⇒ x ≥ – 1
∴ dom f = [- 1 , ∞) = D₁
g(x) is well defined for 1 – x ≥ 0
⇒ x ≤ 1
⇒ x ∈ (-∞, 1]
∴ dom g (-∞, 1] = D₂
∴ D₁ ∩ D₂ = [-1, 1]
(i) f + g
Solution:
f + g: [-1, 1] → R
defined as (f + g) (x)
= f(x) + g(x) = \(\sqrt{1-x}\) + \(\sqrt{1-x}\)

(ii) f – g
Solution:
f – g :[-1, 1] → R defined as
(f – g) (x) = \(\sqrt{1-x}\) – \(\sqrt{1-x}\)

(iii) fg
Solution:
fg : [ – 1, 1] → R defined as
(fg) (x) > f(x) g(x)
\(\sqrt{1-x}\)\(\sqrt{1-x}\) = \(\sqrt{1-x^2}\)

(iv) f/g
Solution:
f/g : [- 1,1) → R defined as
\(\left(\frac{f}{g}\right)\)(x) = \(\frac{f(x)}{g(x)}=\frac{\sqrt{1+x}}{\sqrt{1-x}}\)
for (i) to (iii) domain = [- 1, 1]
but for (iv) domain = [- 1, 1)

Question 12.
If(x) = log_e \(\left(\frac{1-x}{1+x}\right)\), then prove that f(x) + f(y) = \(\left(\frac{x+y}{1+x y}\right)\)
Solution:
f(x) = log\(\left(\frac{1-x}{1+x}\right)\)
f(x) + f(y) = log\(\left(\frac{1-x}{1+x}\right)\) + \(\left(\frac{1-y}{1+y}\right)\)

Question 13.
Let f = {(-1, 4), (2, 7), (-2, 11}. (0,1), (1, 2) be a quadratic polynomial from Z to Z, find f(x).
Solution:
Let f(x) = ax² + by² + C is the quadratic polynomial
f(-1) = 4 ⇒ a – b + c = 4    …..(1)
f(0) = 1⇒ c = 1                   ….(2)
f(1) = 2 ⇒ a + + c = 2        ….(3)
∴ a – b + 1 = 4 and a + b + 1 = 2
⇒ a – b = 3 and a + b = 1
⇒ a = 2, b = -1
f(x) = 2x² – x + 1
f(2) = 8 – 2 + 1 = 7
f(- 2) = 8 + 2 + 1 = 1 1
Thus the required function is f(x) = 2x² – x + 1

Question 14.
Sketch the graphs of the following functions.
(i) f(x) = x³
(ii) f(x) = 1 + \(\frac{1}{x^2}\)
(iii) f(x) = (x-1)²
Solution:
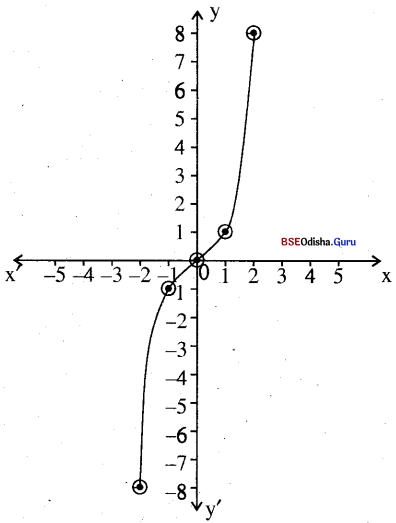
(i) f(x) = x³

x	0	1	2	– 1	-2	3
y	1	1	8	-1	-8	27

(ii) f(x) = 1 + \(\frac{1}{x^2}\)

x	1	-1	2	– 2	3	-3
y	2	2	5/4	5/4	10/9	10/9

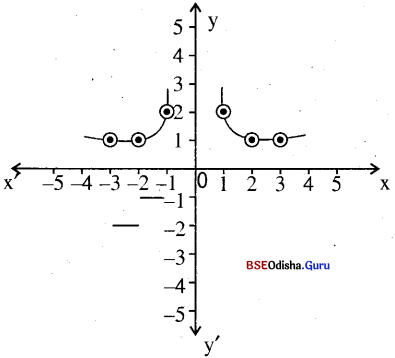
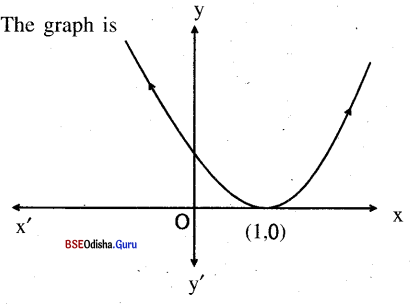
(iii) f(x) = (x-1)²

x	-1	0	1	2	3	4
f(x)	4	1	0	1	4	9