BSE Odisha 8th Class Maths Solutions Algebra Chapter 9 ଚଳନ Ex 9(a)

Odisha State Board BSE Odisha 8th Class Maths Solutions Algebra Chapter 9 ଚଳନ Ex 9(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Maths Solutions Algebra Chapter 9 ଚଳନ Ex 9(a)

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର, ଯେପରି \(\frac { x }{ y }\) = k (ସ୍ଥିରାଙ୍କ) ଏବଂ k = \(\frac { 1 }{ 2 }\)

Solution:

Question 2.
ଚଳନ ସୂତ୍ର ପ୍ରୟୋଗରେ ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।
(a) 3 ଟି କଞ୍ଚା କଦଳୀର ଦାମ୍ 15 ଟଙ୍କା ହେଲେ,
(i) 12 ଟି କଦଳୀର ମୂଲ୍ୟ କେତେ ?
(ii) 25 ଟଙ୍କାରେ କେତୋଟି କଦଳୀ ମିଳିବ ?
Solution:
(i) 3 ଟି କଞ୍ଚା କଦଳୀର ଦାମ୍ 15 ଟଙ୍କା ।
ଏଠାରେ x₁ = 3 ଓ y₁ = 15 ନିଆଯାଉ | x₂ = 12 ଓ y₂ ନିର୍ଣ୍ଣୟ କରିବାକୁ ହେବ ।
ସଳଖ ଚଳନ ସୂତ୍ର ଅନୁଯାୟୀ, \(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\) ⇒ y₂ = \(\frac{\mathrm{x}_2 \mathrm{y}_1}{\mathrm{x}_1}\) = \(\frac{12 \times 15}{3}\) = 60 |
∴ 12 ଟି କଦଳୀର ମୂଲ୍ୟ

(ii) 3 ଟି କଞ୍ଚା କଦଳୀର ଦାମ୍ 15 ଟଙ୍କା ।
ଏଠାରେ x₁ = 3 ଓ y₁ = 25 ନିଆଯାଉ । y₂ = 25 ଓ x₂ ନିର୍ଣ୍ଣୟ କରିବାକୁ ହେବ ।
ସଳଖ ଚଳନ ସୂତ୍ର ଅନୁଯାୟୀ, \(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\) ⇒ x₂ = \(\frac{\mathrm{x}_1 \mathrm{y}_2}{\mathrm{y}_1}\) ⇒ x₂ = \(\frac{3 \times 25}{15}\) = 5
∴ 25 ଟଙ୍କାରେ 5 ଟି କଦଳୀ ମିଳିବ ।

ଦିକଜ୍ ସମଧାର୍ନ ତ୍ପଶାଲା :
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

\(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\) = \(\frac{x_3}{y_3}\) (ସଳଖ ଚଳନର ସଂଜ୍ଞା)
⇒ \(\frac { 3 }{ 15 }\) = \(\frac{12}{y_2}\) = \(\frac{x_3}{25}\) ⇒ \(\frac { 3 }{ 15 }\) = \(\frac{12}{y_2}\) ⇒ y₂ = \(\frac{12 \times 15}{3}\) = 60
ଓ \(\frac { 3 }{ 15 }\) = \(\frac{x_3}{25}\) ⇒ 15x₃ = 3 × 25 ⇒ x₃ = 5
∴ 12 ଟି କଦଳୀର ଦାମ୍ 60 ଟଙ୍କା ଏବଂ 25 ଟଙ୍କାରେ 5 ଟି କଦଳୀ ମିଳିବ ।

(b) ଜଣେ ଶ୍ରମିକର ଦୈନିକ ମଜୁରି 140 ଟଙ୍କା ହେଲେ,
(i) ତାହାର 5 ଦିନର ମଜୁରି କେତେ ?
(ii) 840 ଟଙ୍କା ମଜୁରି ପାଇଁ ସେ କେତେ ଦିନ କାମ କରିବ ?
Solution:
(i) ଜଣେ ଶ୍ରମିକର ଦୈନିକ ମଜୁରି 140 ଟଙ୍କା x = ଦିନ ସଂଖ୍ୟା, y = ଦୈନିକ ମଜୁରି (ଟଙ୍କାରେ)
ଏଠାରେ x₁ = 1 ଓ y₁ = 140 ନିର୍ଣ୍ଣୟ ଏବଂ x₂ = 5 ଓ y₂ ନିର୍ଣ୍ଣୟ ଆବଶ୍ୟକ ।
ସଳଖ ଚଳନ ସୂତ୍ର ଅନୁଯାୟୀ, \(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\) ⇒ \(\frac { 1 }{ 140 }\) = \(\frac{5}{y_2}\) ⇒ y₂ = 5 × 140 = 700
∴ ଶ୍ରମିକଟିର 5 ଦିନର ମଜୁରି 700 ଟଙ୍କା ।

(ii) ଜଣେ ଶ୍ରମିକର ଦୈନିକ ମଜୁରି 140 ଟଙ୍କା ।
ଏଠାରେ x₁ = 1 ଓ y₁ = 140 ନିର୍ଣ୍ଣୟ |
ଦିନ ସଂଖ୍ୟା = x₂ ଓ ମଜୁରି (y₂) = 840 ଟଙ୍କା ।
ସଳଖ ଚଳନ ସୂତ୍ର ଅନୁଯାୟୀ, \(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\) ⇒ \(\frac { 1 }{ x_2 }\) = \(\frac { 140 }{ 840 }\) ⇒ 140x₂ = 840 ⇒ x₂ = \(\frac { 840 }{ 140 }\) = 6 |
∴ 840 ଟଙ୍କା ପାଇଁ ଶ୍ରମିକଟି ‘6′ ଦିନ କାମ କରିବ ।

Question 3.
ସମାନ ଆକାରର 3ଟି ମହମବତିର ଦାମ୍ 24 ଟଙ୍କା ହେଲେ, 120 ଟଙ୍କାରେ ସେହି ଆକାରର କେତୋଟି ମହମବତି ମିଳିବ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶ କଲେ,

ଏଠାରେ ଲକ୍ଷ୍ୟକର, x ∝ y । ତେଣୁ ସଳଖ ଚଳନର ସୂତ୍ର ପ୍ରୟୋଗ ହେବ ।
ସଳଖ ଚଳନ ସୂତ୍ରାନୁଯାୟୀ, \(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\) ⇒ \(\frac { 3 }{ 24 }\) = \(\frac{x_2}{120}\) ⇒ 24x₂ = 120 × 3
⇒ x₂ = \(\frac{120 \times 3}{24}\) = 151
∴ 120 ଟଙ୍କାରେ 15ଟି ଖାତା ମିଳିବ ।

Question 4.
6ଟି ଖାତାର ମୂଲ୍ୟ 90 ଟଙ୍କା । ସେହି ଆକାରର 15ଟି ଖାତାର ମୂଲ୍ୟ କେତେ ? 75 ଟଙ୍କାରେ କେତୋଟି ଖାତା ମିଳିବ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶ କଲେ,

ଏଠାରେ ଲକ୍ଷ୍ୟକର, x ∝ y । ତେଣୁ ସଳଖ ଚଳନର ସୂତ୍ର ପ୍ରୟୋଗ ହେବ ।
ସଳଖ ଚଳନ ସୂତ୍ରାନୁଯାୟୀ, \(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\) = \(\frac{x_3}{y_3}\) ⇒ \(\frac { 6 }{ 90 }\) = \(\frac { 15 }{ y_2 }\) = \(\frac{x_3}{75}\)
⇒ \(\frac { 6 }{ 90 }\) = \(\frac { 15 }{ y_2 }\) ⇒ 6y₂ = 90 × 15 ⇒ y₂ = \(\frac{90 \times 15}{6}\) = 225
ପ୍ରକାଶ, \(\frac { 6 }{ 90 }\) = \(\frac{x_3}{75}\) ⇒ 90x₃ = 6 × 75 ⇒ x₃ = \(\frac{6 \times 75}{90}\) = 5
∴ 15ଟି ଖାତାର ମୂଲ୍ୟ 225 ଟଙ୍କା ଓ 75 ଟଙ୍କାରେ 5ଟି ଖାତା ମିଳିବ ।

Question 5.
ବଜାରରେ 2 କିଲୋଗ୍ରାମ୍ ଆଳୁର ଦାମ୍ 9 ଟଙ୍କା; ତେବେ 5 କିଲୋଗ୍ରାମ୍ ଆଳୁର ମୂଲ୍ୟ କେତେ ? 27 ଟଙ୍କାରେ କେତେ ପରିମାଣର ଆଳୁ ମିଳିବ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶ କଲେ,

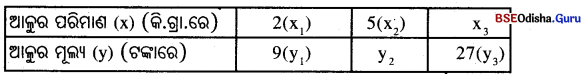
ଏଠାରେ ଲକ୍ଷ୍ୟକର, x ∝ y । ତେଣୁ ସଳଖ ଚଳନର ସୂତ୍ର ପ୍ରୟୋଗ ହେବ ।
ସଳଖ ଚଳନ ସୂତ୍ରାନୁଯାୟୀ, \(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\) = \(\frac{x_3}{y_3}\) ⇒ \(\frac { 2 }{ 9 }\) = \(\frac { 5 }{ y_2 }\) = \(\frac{x_3}{27}\)
⇒ \(\frac { 2 }{ 9 }\) = \(\frac { 5 }{ y_2 }\) ⇒ y₂ = \(\frac { 45 }{ 2 }\) = 22.50
ପ୍ରକାଶ, \(\frac { 2 }{ 9 }\) = \(\frac{x_3}{27}\) ⇒ 9x₃ = 27 × 2
⇒ x₃ = \(\frac{27 \times 2}{9}\) = 6
∴ 5 କିଲୋଗ୍ରାମ୍ ଆଳୁର ମୂଲ୍ୟ ଟ.22.50 ଓ 27 ଟଙ୍କାରେ 6 କିଲୋଗ୍ରାମ୍ ଆଳୁ ମିଳିବ ।

Question 6.
ଗୋଟିଏ ସ୍କୁଟର 3 ଘଣ୍ଟାରେ 120 କିଲୋମିଟର ବାଟ୍ ଯାଇପାରେ । ସେହି ବେଗରେ ୫ ଘଣ୍ଟାରେ କେତେ ବାଟ ଯିବ ଏବଂ ସେହି ବେଗରେ 200 କି.ମି. ବାଟ ଯିବାକୁ କେତେ ସମୟ ଲାଗିବ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

ଏଠାରେ ଲକ୍ଷ୍ୟକର x ∝ y । ତେଣୁ ସଳଖ ଚଳନର ସୂତ୍ର ପ୍ରୟୋଗ ହେବ ।
ସଳଖ ଚଳନ ସୂତ୍ର ଅନୁଯାୟୀ, \(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\) = \(\frac{x_3}{y_3}\) ⇒ \(\frac { 3 }{ 120 }\) = \(\frac { 8 }{ y_2 }\) = \(\frac{x_3}{200}\)
⇒ \(\frac { 3 }{ 120 }\) = \(\frac { 8 }{ y_2 }\) ⇒ 3y₂ = 120 × 8
⇒ y₂ = \(\frac{120 \times 8}{3}\) = 320
ପ୍ରକାଶ, \(\frac { 3 }{ 120 }\) = \(\frac{x_3}{200}\) ⇒ 120x₃ = 600 ⇒ x₃ = \(\frac{600}{120}\) = 5
∴ ସେହି ବେଗରେ 8 ଘଣ୍ଟାରେ 320 କିଲୋମିଟର ଯିବ । 200 କି.ମି. ବାଟ ଯିବାକୁ 5 ଘଣ୍ଟା ସମୟ ଲାଗିବ |

Question 7.
କୁକୁଡ଼ା ଅଣ୍ଡା‘ଡଜନ 15 ଟଙ୍କା ହେଲେ, ଟି ଅଣ୍ଡାର ଦାମ୍ କେତେ ? 10 ଟଙ୍କାରେ କେତୋଟି ଅଣ୍ଡା ମିଳିବ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

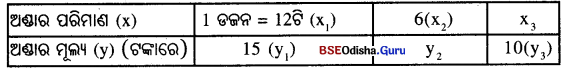
ଏଠାରେ ଲକ୍ଷ୍ୟକର x ∝ y । ତେଣୁ ସଳଖ ଚଳନର ସୂତ୍ର ପ୍ରୟୋଗ ହେବ ।
ସଳଖ ଚଳନ ସୂତ୍ରାନୁଯାୟୀ, \(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\) = \(\frac{x_3}{y_3}\) ⇒ \(\frac { 12 }{ 15 }\) = \(\frac { 6 }{ y_2 }\) = \(\frac{x_3}{10}\)
⇒ \(\frac{12}{15}\) = \(\frac{6}{y_2}\) ⇒ 12y₂ = 15 × 6 ⇒ y₂ = \(\frac{15 \times 6}{12}\) = 7.50
ପ୍ରକାଶ, \(\frac { 12 }{ 15 }\) = \(\frac{x_3}{10}\) ⇒ 15x₃ = 12 × 10 ⇒ x₃ = \(\frac{12 \times 10}{15}\) = 8
∴ ଜୈ ଅଣ୍ଡାର ଦାମ୍ ଟ.7.50 ଏବଂ 10 ଟଙ୍କାରେ ୫ଟି ଅଣ୍ଡା ମିଳିବ ।

Question 8.
15 କି.ମି. ବସ୍‌ରେ ଯିବାପାଇଁ 2 ଟଙ୍କା 25 ପଇସା ଭଡ଼ା ଲାଗେ । ସେହି ବସ୍‌ରେ 80 କି.ମି. ବାଟ ଯିବାକୁ କେତେ ଭଡ଼ା ପଡ଼ିବ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

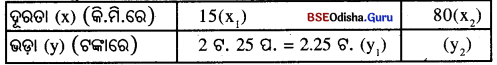
ଏଠାରେ ଲକ୍ଷ୍ୟକର x ∝ y । ତେଣୁ ସଳଖ ଚଳନର ସୂତ୍ର ପ୍ରୟୋଗ ହେବ ।
ସଳଖ ଚଳନ ସୂତ୍ର ଅନୁଯାୟୀ, \(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\)
⇒ \(\frac{15}{2.25}\) = \(\frac{80}{y_2}\) ⇒ 15y₂ = 180 ⇒ y₂ = \(\frac{180}{15}\) = 12
∴ ସେହି ବସ୍‌ରେ 80 କି.ମି. ବାଟ ଯିବାକୁ ଭଡ଼ା 12 ଟଙ୍କା ଲାଗିବ ।

Question 9.
ଗୋଟିଏ ସ୍କୁଟର 45 କି.ମି. ବାଟ ଯିବାରେ 1 ଲିଟର ପେଟ୍ରୋଲ ଆବଶ୍ୟକ କରେ । ସେହି ସ୍କୁଟରରେ 225 କି.ମି. ବାଟ ଯିବାକୁ କେତେ ପେଟ୍ରୋଲ ଆବଶ୍ୟକ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

ଏଠାରେ ଲକ୍ଷ୍ୟକର x ∝ y । ତେଣୁ ସଳଖ ଚଳନର ସୂତ୍ର ପ୍ରୟୋଗ ହେବ ।
ସଳଖ ଚଳନ ସୂତ୍ର ଅନୁଯାୟୀ \(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\) ⇒ \(\frac{45}{1}\) = \(\frac{225}{y_2}\) ⇒ y₂ = \(\frac{225}{45}\) = 5
∴ 225 କି.ମି. ବାଟ ଯିବାପାଇଁ 5 ଲିଟର ପେଟ୍ରୋଲ ଆବଶ୍ୟକ ।

Question 10.
ଗୋଟିଏ ପରିବାରର ଏକ ସପ୍ତାହର ଖାଇବା ଖର୍ଚ୍ଚ 1050 ଟଙ୍କା । ଉକ୍ତ ପରିବାରର ସଦସ୍ୟ ସଂଖ୍ୟା ଅପରିବର୍ତିତ ହେଲେ, 2009 ମସିହା ଫେବୃୟାରୀ ମାସର ଖାଇବା ଖର୍ଚ୍ଚ କେତେ ହେବ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ, [∵ 1 ସପ୍ତାହ = 7 ଦିନ । 2009 ର ଫେବୃୟାରୀ ମାସ = 28 ଦିନ]

ଏଠାରେ ଲକ୍ଷ୍ୟକର x ∝ y । ତେଣୁ ସଳଖ ଚଳନର ସୂତ୍ର ପ୍ରୟୋଗ ହେବ ।
ସଳଖ ଚଳନ ସୂତ୍ର ଅନୁଯାୟୀ, \(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\) ⇒ \(\frac{7}{1050}\) = \(\frac{28}{y_2}\) ⇒ 7y₂ = 1050 × 28 ⇒ y₂ = \(\frac{1050 \times 28}{7}\) = 4200 |
∴ 2009 ମସିହା ଫେବୃୟାରୀ ମାସର ଖାଇବା ଖର୍ଚ୍ଚ 4200 ଟଙ୍କା ହେବ ।

Question 11.
5 ଲିଟର ଖାଇବା ତେଲର ମୂଲ୍ୟ 300 ଟଙ୍କା ହେଲେ, ମାସକୁ 12 ଲିଟର ତେଲ ଖର୍ଚ୍ଚ କରୁଥ‌ିବା ଛାତ୍ରାବାସର ମାସିକ ତେଲ ବାବଦରେ କେତେ ଖର୍ଜ ଦେବାକୁ ପଡ଼ିବ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

ଏଠାରେ ଲକ୍ଷ୍ୟକର x ∝ y । ତେଣୁ ସଳଖ ଚଳନର ସୂତ୍ର ପ୍ରୟୋଗ ହେବ ।
ସଳଖ ଚଳନ ସୂତ୍ର ଅନୁଯାୟୀ, \(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\) ⇒ \(\frac{5}{300}\) = \(\frac{12}{y_2}\) ⇒ y₂ = \(\frac{300 \times 12}{5}\) = 720 |
∴ ମାସକୁ 12 ଲିଟର ତେଲ ଖର୍ଚ୍ଚ କରୁଥିବା ଛାତ୍ରାବାସର ମାସିକ ତେଲ ବାବଦରେ 720 ଟଙ୍କା ଖର୍ଚ୍ଚ ଦେବାକୁ ପଡ଼ିବ ।

Question 12.
50ଟି ଖବରକାଗଜ ବିକିଲେ ଜଣେ ବିକ୍ରେତା 18 ଟଙ୍କା କମିଶନ୍ ପାଆନ୍ତି । ସେ କେତୋଟି କାଗଜ ବିକିଲେ 54 ଟଙ୍କା କମିଶନ୍ ପାଇବେ ? ଦିନକୁ 300 ଟି ଖବରକାଗଜ ବିକିଲେ କେତେ କମିଶନ୍ ମିଳିବ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

ଏଠାରେ ଲକ୍ଷ୍ୟକର x ∝ y । ତେଣୁ ସଳଖ ଚଳନର ସୂତ୍ର ପ୍ରୟୋଗ ହେବ ।
ସଳଖ ଚଳନ ସୂତ୍ର ଅନୁଯାୟୀ, \(\frac{x_1}{y_1}\) = \(\frac{x_2}{y_2}\) = \(\frac{x_3}{y_3}\) ⇒ \(\frac{50}{18}\) = \(\frac{x_2}{54}\) ⇒ \(\frac{300}{y_3}\)
ଦଉମାନ, \(\frac{50}{18}\) = \(\frac{x_2}{54}\) ⇒ 18x₂ = 50 × 54 ⇒ x₂ = \(\frac{50 \times 54}{18}\) = 150
ପୁନଶ୍ଚ, \(\frac{50}{18}\) = \(\frac{300}{y_3}\) ⇒ 50y₃ = 300 × 18 ⇒ y₃ = \(\frac{300 \times 18}{50}\) = 108
∴ ସେ 150ଟି ଖବରକାଗଜ ବିକିଲେ 54 ଟଙ୍କା କମିଶନ୍ ପାଇବେ ଏବଂ ସେ ଦିନକୁ 300ଟି ଖବରକାଗଜ ବିକିଲେ 108 ଟଙ୍କା କମିଶନ୍ ପାଇବେ ।