Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 3 ଜ୍ୟାମିତିରେ ମୌଳିକ ଧାରଣା InText Questions Textbook Exercise Questions and Answers.
BSE Odisha Class 6 Maths Solutions Chapter 3 ଜ୍ୟାମିତିରେ ମୌଳିକ ଧାରଣା InText Questions
ତୁମ ଚାରିପାଖରେ କେଉଁଠାରେ ତୁମେ ବିନ୍ଦୁ ସୃଷ୍ଟି ହେଉଥିବାର ଲକ୍ଷ୍ୟ କରୁଛ, ଲେଖ ।
ସମାଧାନ:
ଆମ ଚାରିପାଖରେ ନିମ୍ନସ୍ଥାନରେ ବିନ୍ଦୁ ସୃଷ୍ଟି ହେଉଥିବାର ଦେଖାଯାଏ –
ଯଥା – ଘରକୋଣ, ଟେବୁଲର ଉପରିଭାଗ ଚାରିକୋଣ, ଡେସ୍କ, ବହି, ଇଟା ପ୍ରଭୃତି କୋଣରେ ବିନ୍ଧୁଥାଏ ।
ପ୍ରଶ୍ନ : ତୁମ ଚାରିପାଖରେ କେଉଁ କେଉଁ ଜିନିଷରେ ତୁମେ ସମାନ୍ତର ସରଳରେଖା ଲକ୍ଷ୍ୟ କରୁଛ ଲେଖ ।
ସମାଧାନ:
(i) ସ୍କେଲ୍ର ଦୁଇଧାର
(ii) ଟେବୁଲ୍ର ଦୁଇଧାର
(iii) ଝରକାର ଦୁଇରେଲିଂ
(iv) ରେଳଧାରଣା
(v) ବହିର ଦୁଇଧାର
କହିଲ ଦେଖ୍:
ସରଳରେଖା, ରଶ୍ମି ଓ ରେଖାଖଣ୍ଡ ମଧ୍ୟରୁ କାହାର ନିର୍ଦ୍ଦିଷ୍ଟ ଦୈର୍ଘ୍ୟ ଅଛି ? କାହିଁକି ?
ସମାଧାନ:
ରେଖାଖଣ୍ଡର ନିର୍ଦ୍ଦିଷ୍ଟ ଦୈର୍ଘ୍ୟ ଅଛି । କାରଣ ରଶ୍ମି ଗୋଟିଏ ଦିଗକୁ ଓ ସରଳରେଖା ଦୁଇ ପାର୍ଶ୍ଵ କୁ ଅସୀମ ଭାବରେ ବିସ୍ତୃତ ।
![]()
ଅନ୍ତଃସୁ ଓ ବହିଃସୁ ବିନ୍ଦୁ:
ଖେଳପଡ଼ିଆର ଚିତ୍ରକୁ ଦେଖ୍ ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନମାନଙ୍କର ଉତ୍ତର ଦିଅ ।

(କ) ଖେଳ ପଡ଼ିଆରେ ଭିତରେ କ’ଣ ସବୁ ଅଛି ?
ସମାଧାନ:
ଖେଳ ପଡ଼ିଆ ଭିତରେ ଖେଳାଳୀ ଓ ଫୁଟବଲ ଅଛି ।
(ଖ) ଖେଳ ପଡ଼ିଆର ବାହାରେ କିଏ ଅଛନ୍ତି ?
ସମାଧାନ:
ଖେଳପଡ଼ିଆର ବାହାରେ ଅନ୍ୟ ପିଲାମାନେ, ଶିକ୍ଷକ ଓ ଶିକ୍ଷୟିତ୍ରୀ ଅଛନ୍ତି ।
(ଗ) ଖେଳ ପଡ଼ିଆର ସୀମାରେ କେଉଁମାନେ ଅଛନ୍ତି ?
ସମାଧାନ:
ଖେଳ ପଡ଼ିଆର ସୀମାରେ ଗୋଲପୋଷ୍ଟ ଓ ପତାକା ଅଛି ।
ତଳେ ଦିଆଯାଇଥିବା ଚିତ୍ରଗୁଡ଼ିକୁ ଦେଖ ଓ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଲେଖ:
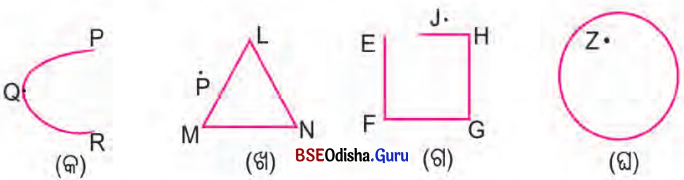
ଚିତ୍ର (କ), (ଖ), (ଗ) ଓ (ଘ)ରେ ପ୍ରଦର୍ଶିତ ଅଞ୍ଚଳମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁ ଅଞ୍ଚଳ ଆବଦ୍ଧ ?
ସମାଧାନ:
ଚିତ୍ର (ଖ) ଓ (ଘ) ଆବଦ୍ଧ ଚିତ୍ର ।
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ______ ଓ ______ ଆବଦ୍ଧ ଚିତ୍ର ।
ସମାଧାନ:
ଚିତ୍ର ‘ଖ’ ଓ ଚିତ୍ର ‘ଘ’ ଆବଦ୍ଧ ଚିତ୍ର ।
(ii) ______ ଓ ______ ଆବଦ୍ଧ ଚିତ୍ର ନୁହେଁ ।।
ସମାଧାନ:
ଚିତ୍ର ‘କ’ ଓ ଚିତ୍ର ‘ଗ’ ଆବଦ୍ଧ ଚିତ୍ର ନୁହେଁ ।
(iii) ______ ଚିତ୍ରର ସୀମା ବକ୍ରରେଖୀ ।
ସମାଧାନ:
‘ଘ’ ଚିତ୍ରର ସୀମା ବକ୍ରରେଖୀ ।
(iv) ______ ଚିତ୍ରର ସୀମା ସରଳରେଖୀ ।
ସମାଧାନ:
‘ଗ’ ଚିତ୍ରର ସୀମା ସରଳରେଖୀ ।
(v) ______ ଚିତ୍ରରେ ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ ଅଛି ଏବଂ ______ ହେଉଛି ବହିଃସ୍ଥ ବିନ୍ଦୁ ।
ସମାଧାନ:
‘ଖ’ ଚିତ୍ରରେ ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ ଅଛି ଏବଂ P ହେଉଛି ବହିଃସ୍ଥ ବିନ୍ଦୁ ।
(vi) ______ ଚିତ୍ରରେ ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ଅଛି ଏବଂ ______ ହେଉଛି ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ।
ସମାଧାନ:
‘ଘ’ ଚିତ୍ରରେ ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ଅଛି ଏବଂ Z ହେଉଛି ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ।
![]()
ନିମ୍ନ ପ୍ରଶ୍ନର ଉତ୍ତର ଦିଅ ।
ଚିତ୍ର (କ) ରେ ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ ଦର୍ଶାଇ ପାରିବ କି ?
ସମାଧାନ:
ନାହିଁ, ଉନ୍ମୁକ୍ତ ଚିତ୍ର ହୋଇ ଥିବାରୁ ଅନ୍ତସ୍ଥ ଓ ବହିଃସ୍ଥ ବିନ୍ଦୁ ନାହିଁ ।
କେଉଁ କେଉଁ ଚିତ୍ରରେ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ବା ବହିଃସ୍ଥ ବିନ୍ଦୁ ଦର୍ଶାଇ ପାରିବ ନାହିଁ ?
ସମାଧାନ:
ଚିତ୍ର (କ) ଓ (ଗ) ରେ ଅନ୍ତଃସ୍ଥ ଓ ବହିଃସ୍ଥ ବିନ୍ଦୁ ଦର୍ଶାଇ ହେବ ନାହିଁ ।
କେବଳ ଆବଦ୍ଧ ଚିତ୍ରରେ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ତଥା ବହିଃସ୍ଥ ବିନ୍ଦୁ ଅଛନ୍ତି ।
ତୁମ ପରିବେଶରେ ତୁମେ କେଉଁ କେଉଁଠାରେ କୋଣ ସୃଷ୍ଟି ହେବାର ଦେଖୁଛ ଲେଖ ।
ସମାଧାନ:
ଶ୍ରେଣୀଗୃହର ବାରଣ୍ଡା, ଘରର କୋଠରି, ବହି, ଖାତା, ରାସ୍ତାର ଛକଠାରେ କୋଣ ସୃଷ୍ଟି ହୁଏ ।
ଚିତ୍ର ଦେଖ ଓ ପ୍ରଶ୍ନମାନଙ୍କର ଉତ୍ତର ଦିଅ:
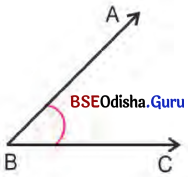
(i) ଚିତ୍ରରେ ଥିବା ରଶ୍ମିଦ୍ଵୟର ନାମ କ’ଣ ?
ସମାଧାନ:
\(\overrightarrow{\mathrm{BA}}\), \(\overrightarrow{\mathrm{BC}}\)
(ii) ରଶ୍ମିଦ୍ଵୟର ସାଧାରଣ ଆଦ୍ୟବିନ୍ଦୁ କିଏ ?
ସମାଧାନ:
B
(iii) ରଶ୍ମି BA କେଉଁ ଦିଗରେ ସସୀମ ?
ସମାଧାନ:
A
(iv) \(\overrightarrow{\mathrm{BC}}\) କେଉଁ ଦିଗରେ ସସୀମ ?
ସମାଧାନ:
C
ତୁମେ ଗୋଟିଏ କୋଣ ଅଙ୍କନ କରି ତାହାର ଅନ୍ତର୍ଦେଶକୁ ରଙ୍ଗଦେଇ ଚିହ୍ନାଅ। କୋଣର ଗୋଟିଏ ଅନ୍ତଃସୁ ବିନ୍ଦୁ ଓ ଗୋଟିଏ ବହିଃସୁ ବିନ୍ଦୁକୁ ମଧ୍ଯ ଦର୍ଶାଅ ।
ସମାଧାନ:
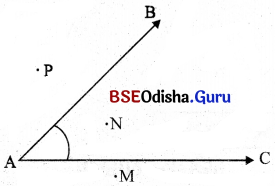
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ∠BAC ର N ବିନ୍ଦୁଟି ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ।
N, ବିନ୍ଦୁପରି ∠BAC ର ଆହୁରି ଅସଂଖ୍ୟ ବିନ୍ଦୁ ଅଛି ।
P ଓ M ବିନ୍ଦୁ ∠BAC ର ବହିଃସ୍ଥ ବିନ୍ଦୁ ।
ଏହିଭଳି ଅନେକ ବହିଃସ୍ଥ ଅଛି ।
ଗୋଟିଏ କୋଣ ଏହାର ଅନ୍ତଃସ୍ଥ ଓ ବହିଃସ୍ଥ ଅଂଶକୁ ପୃଥକ୍ କରେ ।
ସନ୍ନିହିତ କୋଣ :
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ର ଦେଖି ଉତ୍ତର ଲେଖ ।
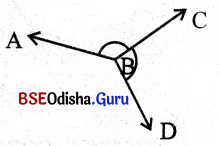
(i) ∠ABC ଓ ∠CBD ର ଶୀର୍ଷବିନ୍ଦୁ ନାମ କ’ଣ ?
ସମାଧାନ:
ଶୀର୍ଷବିନ୍ଦୁ B
(ii) ଏହି କୋଣଦ୍ଵୟର ସାଧାରଣ ବାହୁ କିଏ ?
ସମାଧାନ:
ସାଧାରଣ ବାହୁ \(\overrightarrow{\mathrm{BC}}\)
(iii) କେଉଁ ରଶ୍ମିର ବିପରୀତ ପାର୍ଶ୍ବରେ କୋଣଦ୍ୱୟର ଅନ୍ତର୍ଦ୍ଦେଶଦ୍ବୟ ଅବସ୍ଥିତ ?
ସମାଧାନ:
\(\overrightarrow{\mathrm{BC}}\) ବାହୁର ବିପରୀତ ପାର୍ଶ୍ଵରେ କୋଣଦ୍ୱୟର ଅନ୍ତର୍ଦେଶ ଅଛି ।
(iv) ∠ABC ଓ ∠CBD କୋଣଦ୍ୱୟର ଅନ୍ତର୍ଦ୍ଦେଶର କୌଣସି ସାଧାରଣ ଅଂଶ ଅଛି କି ?
ସମାଧାନ:
ନାହିଁ
(v) ତୁମେ ଦୁଇଟି ସନ୍ନିହିତ କୋଣ ଅଙ୍କନକରି ତାହାର ନାମକରଣ କର ।
ସମାଧାନ:
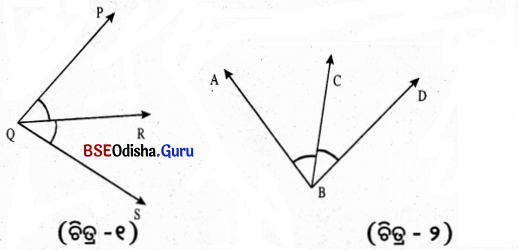
ଚିତ୍ର (୧) ରେ ∠POR ଓ ∠RQS ଏବଂ ଚିତ୍ର (୨) ରେ ∠ABC ଓ ∠CBD କୋଣଦ୍ଵୟ ସନ୍ନିହିତ କୋଣ ।
![]()
(vi) ତୁମ ଖାତାରେ ସରଳ ରୈଖିକ ଯୋଡ଼ି ଅଙ୍କନ କର । କୋଣଦୁଇଟିର ପରିମାଣର ସମଷ୍ଟି ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
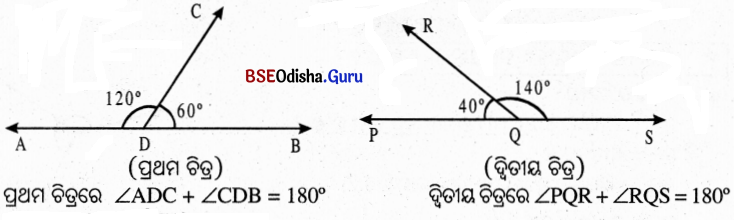
ପ୍ରୁତୀପ କୋଣ ବା ବିପରୀତ କୋଣ:
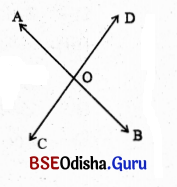
(i) \(\overleftrightarrow{\mathrm{AB}}\) ଓ \(\overleftrightarrow{\mathrm{CD}}\) ଦ୍ଵୟ ପରସ୍ପରକୁ କେଉଁ ବିନ୍ଦୁରେ ଛେଦ କରୁଛନ୍ତି ?
ସମାଧାନ:
ଠ ବିନ୍ଦୁରେ ।
(ii) ∠AOD ର କେତୋଟି ସନ୍ନିହିତ କୋଣ ଅଛି ଓ ସେ କୌଣିଗୁଡ଼ିକର ନାମ କ’ର୍ଣ ?
ସମାଧାନ:
∠AOD ର ଦୁଇଟି ସନ୍ନିହିତ କୋଣ ଅଛି । ସେଗୁଡ଼ିକ ∠AOC ଓ ∠BOD
(iii) କେଉଁ କୋଣ ∠AOD ର ସନ୍ନିହିତ ନୁହେଁ ?
ସମାଧାନ:
∠BOC
(iv) ତୁମେ ଦୁଇଟି ସରଳରେଖା \(\overleftrightarrow{\mathrm{XY}}\) ଓ \(\overleftrightarrow{\mathrm{PQ}}\) ନିଅ। ଯେପରି ସେମାନେ ପରସ୍ପରକୁ K ବିନ୍ଦୁରେ ଛେଦ କରିବେ । ତୁମେ ପାଇଥବା ଚିତ୍ରରେ ଦୁଇ ଯୋଡ଼ା ପ୍ରତୀପ ବା ବିପରୀତ କୋଣ ଚିହ୍ନାଅ ।
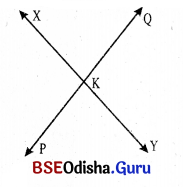
ସମାଧାନ:
∠XKQ ଓ ∠PKY ପ୍ରତୀପ ବା ବିପରୀତ କୋଣ ।
∠XKP ଓ ∠QKY ପ୍ରତୀପ ବା ବିପରୀତ କୋଣ ।
ଅନୁପୂରକ କୋଣ:
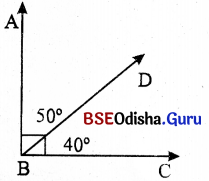
(i) ∠ABC ବ୍ୟତୀତ ଚିତ୍ରରେ ଅନ୍ୟ ଦୁଇଟି କୋଣର ନାମ କ’ଣ ?
ସମାଧାନ:
∠ABD ଓ ∠DBC
(ii) ∠ABD ର ପରିମାଣ + ∠DBC ର ପରିମାଣ = କେତେ ?
ସମାଧାନ:
∠ABD ର ପରିମାଣ + ∠DBC ର ପରିମାଣ = 50° + 40° = 90°
![]()
ପରିପୂରକ କୋଣ:
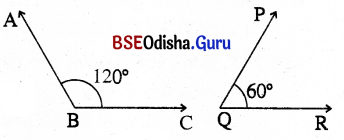
(i) ଚିତ୍ରର କୋଣଦ୍ୱୟର ନାମ କ’ଣ ?
ସମାଧାନ:
∠ABC ଓ ∠PQR
(ii) ଏହି କୋଣ ଦ୍ଵୟର ପରିମାଣର ସମଷ୍ଟି ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
∠ABC = 120°, ∠PQR = 60°
