Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 2 ଦ୍ବିଘାତ ସମୀକରଣ Ex 2(a) Textbook Exercise Questions and Answers.
BSE Odisha Class 10 Maths Solutions Algebra Chapter 2 ଦ୍ବିଘାତ ସମୀକରଣ Ex 2(a)
Question 1.
ନିମ୍ନଲିଖ ଉକ୍ତିଗୁଡ଼ିକରେ ଥିବା ତ୍ରୁଟିକୁ ସଂଶୋଧନ କରି ଲେଖ ।
(i) x² – 4x + 4 = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ ବାସ୍ତବ ଓ ଭିନ୍ନ ।
(ii) x² – 5x + 6 = 0 ସମୀକରଣର ପ୍ରଭେଦକ 2 ଅଟେ ।
(iii) ax? + bx – c = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟର ସମଷ୍ଟି \(\frac{c}{a}\)।
(iv) ax’ + bx + c = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟର ଗୁଣଫଳ \(\frac{b}{a}\)।
(v) 1 ଓ -1 ମୂଳ ବିଶିଷ୍ଟ ଦ୍ୱିଘାତ ସମୀକରଣଟି x² + 1 = 0 ।
(vi) x² = 0 ଦ୍ୱିଘାତ ସମୀକରଣର ମୂଳ ସମାନ ନୁହଁନ୍ତି ।
(vii) 3x² – 2x – 1 = 0 ସମୀକରଣର ମୂଳ ଦ୍ଵୟର ସମଷ୍ଟି \(– \frac{3}{2}\)।
(viii) 3x² – 2x – 1 = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟର ଗୁଣଫଳ \(\frac{1}{3}\)।
ଉ-
(i) x² – 4x + 4 = 0 ସମୀକରଣର ମୂଳଦ୍ବୟ ବାସ୍ତବ ପରିମେୟ ଓ ସମାନ ।
(ii) x² – 5x + 6 = 0 ସମୀକରଣର ପ୍ରଭେଦକ 1 ଅଟେ ।
(iii) ax² + bx – c = 0 ମୂଳଦ୍ଵୟର ସମଷ୍ଟି \(\frac{-b}{a}\)।
(iv) ax² + bx + c = 0 ସମୀକରଣର ମୂଳଦ୍ବୟର ଗୁଣଫଳ \(\frac{c}{a}\)।
(v) 1 ଓ – 1 ମୂଳବିଶିଷ୍ଟ ଦ୍ୱିଘାତ ସମୀକରଣଟି x² – 1 = 0।
(vi) x² = 0 ଦ୍ବିଘାତ ସମୀକରଣର ମୂଳଦ୍ଵୟ ସମାନ ଅଟନ୍ତି ।
(vii) 3x² – 2x – 1 = 0 ସମୀକରଣର ମୂଳଦ୍ବୟର ସମଷ୍ଟି \(\frac{2}{3}\)
(viii) 3x² – 2x – 1 = 0 ସମୀକରଣର ମୂଳଦ୍ବୟର ଗୁଣଫଳ \(\frac{-1}{3}\)।
(i) ଏଠାରେ a = 1, b = -4, c = 4
ପ୍ରଭେଦକ (D) = b² – 4ac = (-4)² – 4 × 1 × 4 = 16 – 16 = 0
∴ ମୂଳଦ୍ବୟ ବାସ୍ତବ ଓ ସମାନ ।
(ii) ଏଠାରେ a = 1, b=-5, c = 6
ପ୍ରଭେଦକ (D) = b² – 4ac = (- 5)² – 4 (1) (6) = 25 – 24 = 1
(iii) ax² + bx – c = 0 ମୂଳଦ୍ଵୟର ସମଷ୍ଟି \(\frac{-b}{a}\)।
(iv) ax² + bx + c = 0 ମୂଳଦ୍ବୟର ଗୁଣଫଳ \(\frac{c}{a}\)।
(v) ମୂଳବିଶିଷ୍ଟ ଦ୍ୱିଘାତ ସମୀକରଣ, x² – (α + ß) x + αß = 0
⇒ x² – { 1 + (- 1)} x + 1 (-1) = 0 ⇒ x² – 1 = 0
(vi) x = 0 ଦ୍ୱିଘାତ ସମୀକରଣ ମୂଳଦ୍ଵୟ ସମାନ ଅଟନ୍ତି । (କାରଣ ପ୍ରଭେଦକ (D) = 0)
(vii) ଏଠାରେ a = 3, b = -2, c = -1 ମୂଳଦ୍ଵୟ ସମାନ = \(\frac{-b}{a}\) = \(\frac{-(-2)}{a}\) = \(\frac{2}{3}\)
(viii) 3x² – 2x-1=0 ଏଠାରେ a = 3, b = -2, c = 1 ମୂଳଦ୍ବୟର ଗୁଣଫଳ \(\frac{c}{a}\) = \(\frac{-1}{3}\)
![]()
Question 2.
ନିମ୍ନଲିଖୂ ପ୍ରଶ୍ନମାନଙ୍କର ସଂକ୍ଷିପ୍ତ ଉତ୍ତର ଦିଅ ।
(i) ଗୋଟିଏ ଦ୍ବିଘାତ ସମୀକରଣର ମୂଳଦ୍ଵୟ 3 ଓ -5 ହେଲେ, ସମୀକରଣଟି ନିରୂପଣ କର ।
(ii) mx² – 2x + (2m – 1) = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟର ଗୁଣଫଳ 3 ହେଲେ, m ର ମାନ ନିରୂପଣ କର ।
(iii) x² – px + 2 = 0 ସମୀକରଣର ଗୋଟିଏ ମୂଳ 2 ହେଲେ, p ର ମାନ ନିରୂପଣ କର ।
(iv) 4x² – 2x + c = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ ଏକ ଓ ଅଭିନ୍ନ ହେଲେ, c ର ମାନ ନିରୂପଣ କର ।
(v) 5x² + 2x + k = 0 ସମୀକରଣର ଗୋଟିଏ ମୂଳ – 2 ହେଲେ, k ର ମାନ ନିରୂପଣ କର ।
(vi) x² – kx + 6 = 0 ସମୀକରଣର ଗୋଟିଏ ମୂଳ 3 ହେଲେ, k ର ମାନ ନିରୂପଣ କର ।
(vii) 2x² + kx + 3 = 0 ସମୀକରଣର ଦୁଇଟି ମୂଳ ବାସ୍ତବ ଓ ସମାନ ହେଲେ, k ର ମାନ ନିରୂପଣ କର ।
ସମାଧାନ :
(i) ଗୋଟିଏ ଦ୍ଵିଘାତ ସମୀକରଣର ମୂଳଦ୍ଵୟ 3 ଓ – 5 । ଅର୍ଥାତ୍ α = 3 ଓ ß = – 5
![]() x² – (α + ß) x + αß = 0
x² – (α + ß) x + αß = 0
⇒ x² – (3 – 5) x + (3)(-5) = 0 ⇒ x² + 2x – 15 = 0
![]()
(ii) mx² – 2x + (2m – 1) = 0 ମୂଳଦ୍ଵୟର ଗୁଣଫଳ = 3
ଏଠାରେ a = m, b = – 2, c = 2m – 1
ମୂଳଦ୍ବୟର ଗୁଣଫଳ = \(\frac{c}{a}\) ⇒ 3 \(\frac{2m-1}{m}\)
⇒ 3m = 2m – 1 ⇒ 3m – 2m = 1 ⇒ m = -1
∴ ଦତ୍ତ ସମୀକରଣର ମୂଳଦ୍ଵୟର ଗୁଣଫଳ 3 ହେଲେ m = -1 ହେବ ।
(iii) x² – px + 2 = 0 ସମୀକରଣର ଗୋଟିଏ ମୂଳ 2।
⇒ 2² – p(2) + 2 =0 ⇒ 4 – 2p + 2 = 0 ⇒ 6 = 2p ⇒ p = \(\frac{6}{2}\) = 3
∴ pର ମାନ = 3
(iv) 4x² – 2x + c = ଫିର ମୂଳଦ୍ବୟ ଏକ ଓ ଅଭିନ୍ନ । ଏଠାରେ a = 4, b = – 2, c = c
ପ୍ରଭେଦକ (D) = 0 ⇒ b² – 4ac = 0 ⇒ (-2)² – 4 (4) c = 0 ⇒ 4 – 16c = 0
⇒ -16c = -4 = c = – \(\frac{-4}{16}=\frac{1}{4}\)
∴ c = \(\frac{1}{4}\)
∴ ଦତ୍ତ ସମୀକରଣର ମୂଳଦ୍ଵୟ ଏକ ଏବଂ ଅଭିନ୍ନ ହେଲେ c ର ମାନ \(\frac{1}{4}\) ହେବ।
(v) 5x² + 2x + k = 0 ସମୀକରଣର ଗୋଟିଏ ମୂଳ – 2 ।
⇒ 5(- 2)² + 2(- 2) + k = 0 ⇒ 20 – 4 + k = 0 ⇒ 16 + k = 0 ⇒ k = -16
∴ ‘k’ ର ମାନ -16 ପାଇଁ ଦତ୍ତ ସମୀକରଣର ଗୋଟିଏ ମୂଳ -2 ହେବ ।
(vi) x² – kx + 6 = 0 ସମୀକରଣର ଗୋଟିଏ ମୂଳ 3।
⇒ 3² – 3k + 6 = 0 ⇒ 9 – 3k + 6 = 0 ⇒ -3k = -15 ⇒ \(\frac{-15}{-3}=5\)
∴ ଦତ୍ତ ସମୀକରଣର ଗୋଟିଏ ମୂଳ 3 ହେଲେ k ର ମାନ 5 ହେବ ।
(vii) 2x² + kx + 3 = 0, ଏଠାରେ a = 2, b = k, c = 3
ସମୀକରଣର ମୂଳଦ୍ୱୟ ବାସ୍ତବ ଓ ସମାନ ହେଲେ b² – 4ac = 0
⇒ k² – 4 (2) (3) = 0 ⇒ k² – 24 = 0 ⇒ k² = 24 ⇒ k = ±√24 ⇒ k = ± 2√6
∴ ଦତ୍ତ ସମୀକରଣର ମୂଳଦ୍ଵୟ ବାସ୍ତବ ଓ ସମାନ ହେଲେ k ର ମାନ ±2√6 ହେବ ।
![]()
Question 3.
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନପାଇଁ ଥିବା ସମ୍ଭାବ୍ୟ ଉତ୍ତରଗୁଡ଼ିକ ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
(i) ନିମ୍ନଲିଖ୍ ସମୀକରଣମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁଟି x ରେ ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ ?
(a) x² – x – 12 = 0
(b) x² + 12 = 3
(c) x + = x²
(d)x (x – 1 ) (x + 5) = 0
(ii) 7x² – 9x + 2 = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟର ସ୍ବରୂପ କ’ଣ ?
(a) ବାସ୍ତବ ସଂଖ୍ୟା ଓ ପରସ୍ପରଠାରୁ ପୃଥକ୍
(b) ବାସ୍ତବ ସଂଖ୍ୟା ଏବଂ ଏକ ଓ ଅଭିନ୍ନ
(c) ବାସ୍ତବ ହେବେ ନାହିଁ
(d) ଏଥୁରୁ କେଉଁଟି ନୁହେଁ
(iii) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି – 6 ଓ 8 ମୂଳ ବିଶିଷ୍ଟ ଦ୍ବିଘାତ ସମୀକରଣ ?
(a) (x + 6) (x+8)= 0
(b) (x + 6) (x – 8) = 0
(c) (x – 6) (x + 8) = 0
(d) (x – 6) (x – 8) = 0
(iv) 3x² + 2√5 x – 5 = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ α ଓ ß ଓ ହେଲେ αß ର ମୂଲ୍ୟ କେତେ ?
(a) 3
(b) 2√5
(c) \(\frac{2√5}{3}\)
(d) \(\frac{-5}{3}\)
(v) 4x – 2x + 2 = 0 ସମୀକରଣର ମୂଳଦ୍ବୟ α ଓ ß ହେଲେ α + ß ର ମୂଲ୍ୟ କେତେ ?
(a) \(\frac{1}{16}\)
(b) 4
(c) \(\frac{1}{2}\)
(d) -8
(vi) 4x + 3x + 7 = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ α ଓ ß ହେଲେ \(\frac{1}{α}+\frac{1}{ß}\) ର ହେଲେ କେତେ ?
(a) \(\frac{3}{7}\)
(b) \(– \frac{3}{7}\)
(c) \(\frac{7}{3}\)
(d) \(– \frac{7}{3}\)
(vii) ଗୋଟିଏ ଦ୍ବିଘାତ ସମୀକରଣର ମୂଳଦ୍ଵୟର ସମଷ୍ଟି ଓ ଗୁଣଫଳ ଯଥାକ୍ରମେ 4 ଓ \(\frac{5}{2}\) ହେଲେ ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ?
(a) 2x² + 8x + 5 = 0
(b) 2x² – 8x + 5 = 0
(c) 2x² + 8x – 5=0
(d) 2x² – 8x – 5 = 0
ଉ-
(i) x² – x – 12 = 0
(ii) ବାସ୍ତବ ସଂଖ୍ୟା ଓ ପରସ୍ପରଠାରୁ ପୃଥକ୍
(iii) (x +6) (x – 8) = 0
(iv) \(\frac{-5}{3}\)
(v) \(\frac{1}{2}\)
(vi) \(– \frac{3}{7}\)
(vii) 2x² – 8x + 5 = 0
![]()
Question 4.
ନିମ୍ନଲିଖୂତ ଦ୍ବିଘାତ ସମୀକରଣମାନଙ୍କୁ ପୂର୍ବ ବର୍ଗରେ ପରିଣତ କରି ସମାଧାନ କର ।
(i) x² + x – 6 = 0
(ii) 2x² – 9x + 4 = 0
(iii) 14x² + x – 3 = 0
(iv) 3x² – 32x + 12=0
(v) x² + 2px – 3qx – 6pq = 0
(vi) √3x² + 10x + 8√3 = 0
(vii) 25x² + 30x + 7 = 0
(viii) 3a²x² + 8abx + 4b² = 0 (a ≠ 0)
(ix) x² + ax + b = 0
(x) x² + bx = a² – ab
ସମାଧାନ :
(i)

(ii)
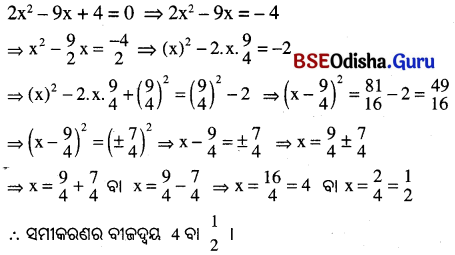
(iii)

(iv)

(v) x² + 2px – 3qx – 6pq = 0
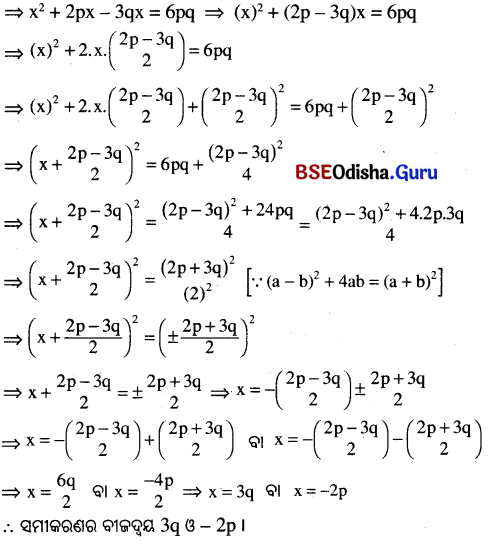
![]()
(vi) √3x² + 10x + 8√3 = 0

(vii) 25x² + 30x + 7 = 0
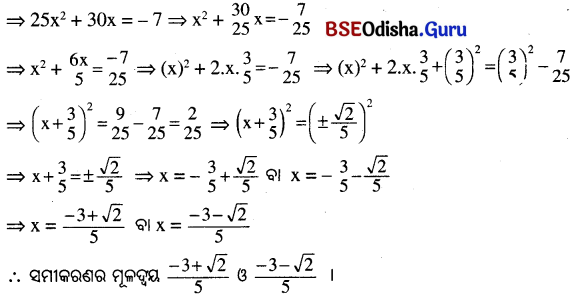
(viii) 3a²x² + 8abx + 4b² = 0 (a ≠ 0)

(ix) x² + ax + b = 0
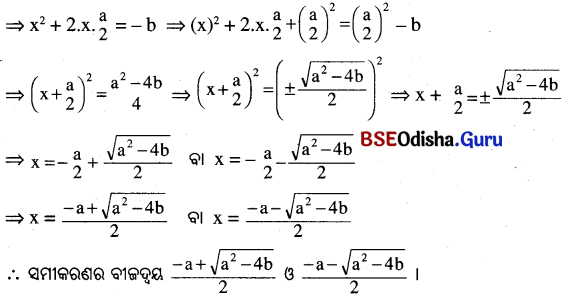
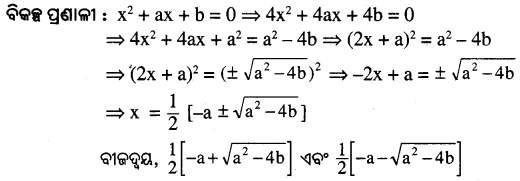
(x) x² + bx = a² – ab

Question 5.
ଦ୍ଵିଘାତ ସୂତ୍ର ପ୍ରୟୋଗ କରି ନିମ୍ନଲିଖ ସମୀକରଣମାନଙ୍କର ବୀଜ ବା ମୂଳ ନିରୂପଣ କରି ।
(i) 4x² – 11x + 6 = 0
(ii) (2x – 1)(x – 2) = 0
(iii) x² – (1+√2)x+ 2 = 0
(iv) a(x² + 1) = x(a2 + 1), a ≠ 0
(v) 6x² + 11x + 3 = 0
(vi) 2x² + 41x – 115 = 0
(vii) 12x² +x – 6 = 0
(viii) (6x + 5)(x – 2) = 0
(ix) 15x² – x – 8 = 0
(x) (x + 5)(x – 5) = 39
ସମାଧାନ :
(i) 4x² – 11x + 6 = 0

(ii) (2x – 1)(x – 2) = 0
⇒ 2x² – 4x -x + 2 = 0 ⇒ 2x² – 5x + 2 = 0
ଏଠାରେ a = 2, b = -5, c = 2
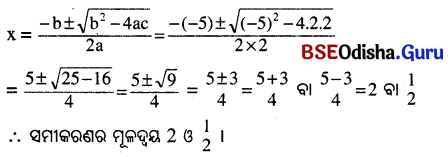
(iii) x² – (1+√2)x+ 2 = 0
ଏଠାରେ a = 1, b = – (1+√2), c = √2
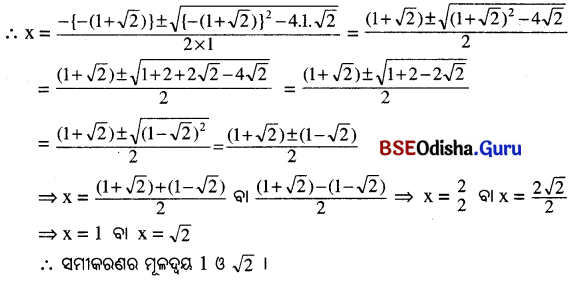
(iv) a(x² + 1) = x(a² + 1) ⇒ a(x² + 1) – x(a² + 1) = 0
⇒ ax² + a – x(a² + 1) = 0 ⇒ ax² – x(a² + 1) + a = 0
ଏଠାରେ a = a, b = -(a² + 1), c = a

(v) 6x² + 11x + 3 = 0
ଏଠାରେ a = 6, b = 11, c = 3

(vi) 2x² + 41x – 115 = 0
ଏଠାରେ a = 2, b = 41, c = -115

(vii) 12x² +x – 6 = 0
ଏଠାରେ a = 12, b = 1, c = -6

(viii) (6x + 5)(x – 2) = 0 ⇒ 6x² -12x + 5x – 10 = 0 ⇒ 6x² -7x – 10 = 0
ଏଠାରେ a = 6, b = -7, c = -10
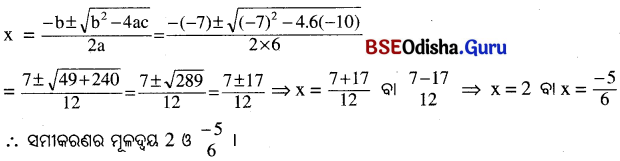
(ix) 15x² – x – 8 = 0
ଏଠାରେ a = 15, b = -1, c = -8

(x) (x + 5)(x – 5) = 39 ⇒ x² – 25 = 39 ⇒ x² – 25 – 39 = 0 ⇒ x² – 64 = 0
ଏଠାରେ a = 1, b = 0, c = -64
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}=\frac{0 \pm \sqrt{0^2-4(1) 64}}{2(1)}=\frac{0 \pm \sqrt{256}}{2}=\frac{\pm 16}{2}=\pm 8\)
⇒ x = 8 ବ। x = -8
∴ ସମୀକରଣର ମୂଳଦ୍ଵୟ 8 ଓ -8 ।
![]()
Question 6.
ଯଦି 4x² – 13x + k = 0 ସମୀକରଣର ଗୋଟିଏ ମୂଳ ଅପରଟିର 12 ଗୁଣ ହେଲେ kରେ ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ :
ମନେକର 4x² – 13x + k = 0 ସମୀକରଣର ଗୋଟିଏ ମୂଳ । ଏବଂ ଅନ୍ୟଟି 12α ।
ଏଠାରେ a = 4, b = 13 6 c = k
∴ ମୂଳଦ୍ବୟର ସମଷ୍ଟି = \(\frac{-b}{a}\) ⇒ α + 12α = \(\frac{-(-13)}{4}\) ⇒ 13α = \(\frac{13}{4}\) ⇒ α = \(\frac{13}{4}\) × \(\frac{1}{13}\) = \(\frac{1}{4}\)
ମୂଳଦ୍ବୟର ଗୁଣଫଲ = \(\frac{-c}{a}\) ⇒ α.12α = \(\frac{k}{4}\) ⇒ 12α² = \(\frac{k}{4}\) ⇒ 12 × (\(\frac{1}{4}\))² = \(\frac{k}{4}\) ⇒ \(\frac{12}{16}\) = \(\frac{k}{4}\) ⇒ 16k = 48 ⇒ k = 3
∴ kର ମାନ 3 ହେଲେ ସମୀକରଣର ଗୋଟିଏ ମୂଳ ଅପରଟିର 12 ଗୁଣ ହେବ ।
Question 7.
x² – 5x + p = 0 ସମୀକରଣର ଗୋଟିଏ ମୂଳ ଅପରଟି ଅପେକ୍ଷା 3 ଅଧିକ ହେଲେ pର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ :
ମନେକର x² – 5x + p = 0 ସମୀକରଣର ଗୋଟିଏ ମୂଳ α ଓ ଅନ୍ୟଟି α + 3
∴ ମୂଳଦ୍ବୟର ସମଷ୍ଟି = α + α + 3 = \(\frac{-(-5)}{1}\)
⇒ 2α + 3 = 5 ⇒ 2α = 5 – 3 = 2 ⇒ α = \(\frac{2}{2}\) = 1
α ର ମାନ ସମୀକରଣରେ ବସାଇଲେ 1² – 5 (1) + p = 0
⇒ 1 – 5 + p = 0 ⇒ p – 4= 0 ⇒ p = 4
∴ p ର ମାନ 4 ହେଲେ ଗୋଟିଏ ମୂଳ ଅପରୂଟି ଅପେକ୍ଷା 3 ଅଧିକ ହେବ ।
Question 8.
ଯଦି 2x² – 5x + 3 = 0 ସମୀକରଣର ମୂଳଦ୍ୱୟ α ଓ ß ହୁଏ ତେବେ α²ß + αß²ର ମୂଲ୍ୟ ନିରୂପଣ ‘କର ।
ସମାଧାନ :
2x² – 5x + 3= 0 ସମୀକରଣର ମୂଳଦ୍ୱୟ α ଓ ß।
ମୂଳଦ୍ଵୟର ସମଷ୍ଟି = α + ß = \(\frac{-(-5)}{2}\) ⇒ α + ß = \(\frac{5}{2}\)
ମୂଳଦ୍ବୟର ଗୁଣଫଲ = αß = \(\frac{3}{2}\)
∴ α²ß + αß² = αß (α + ß)\(\frac{3}{2}\)(\(\frac{5}{2}\)) = \(\frac{15}{4}\)
Question 9.
ଯଦି 2x² – 6x + 3 = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ α ଓ ß ହୁଏ, ତେବେ (α + 1) (ß + 1) ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ :
2x² – 6x + 3= 0 ସମୀକରଣର ମୂଳଦ୍ୱୟ α ଓ ß।
ମୂଳଦ୍ବୟର ସମଷ୍ଟି = α + ß = \(\frac{-(-6)}{2}\) = \(\frac{6}{2}\) = 3
ମୂଳଦ୍ବୟର ଗୁଣଫଲ = αß = \(\frac{3}{2}\)
∴ (α + 1) (ß + 1) = αß + α + ß + 1 = \(\frac{3}{2}\) + 3 + 1 = \(\frac{3+6+2}{2}\) = \(\frac{11}{2}\)
∴ (α + 1) (ß + 1) = \(\frac{11}{2}\)
Question 10.
ଯଦି 2x² – (p + 1) x + p – 1 = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟର ଅନ୍ତର ଓ ଗୁଣଫଳ ସମାନ ହେଲେ pର ମାନ ନିରୂପଣ କର ।
ସମାଧାନ :
ମନେକର 2x² – (p + 1) x + (p – 1) = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ α ଓ ß।
ବୀଜଦ୍ଵୟର ସମଷ୍ଟି α + ß = \(\frac{-{-(p+1)}}{2}\) = \(\frac{p+1}{2}\) ଏବଂ αß = \(\frac{p-1}{2}\)
ପ୍ରଶାନୁସାରେ ବୀଜଦ୍ଵୟର ଅନ୍ତର, ବୀଜଦ୍ୱୟର ଗୁଣଫଳ ସହ ସମାନ ।
∴ α – ß = aß ⇒ (α – ß)² = (aß)² ⇒ (α + B)² – 4aß = (αß)²
⇒ (\(\frac{p+1}{2}\))² – 4(\(\frac{p-1}{2}\)) ⇒ (\(\frac{p-1}{2}\))² = (\(\frac{p+1}{2}\))² – (\(\frac{p-1}{2}\))² = 4 (\(\frac{p-1}{2}\))
⇒ p . 1 = 2p – 2 ⇒ p = 2
∴ ଦତ୍ତ ସମୀକରଣର ମୂଳଦ୍ଵୟର ଅନ୍ତର ଓ ଗୁଣଫଳ ସମାନ ହେଲେ p ର ମାନ 2 ହେବ ।
Question 11.
ଯଦି 5x² – 3x – 2 = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ α ଓ ß ହୁଏ, ତେବେ ପ୍ରମାଣ କର ଯେ α³ + ß³ = \(\frac{117}{125}\)
ସମାଧାନ :
5x²-3x-2=0 ସମୀକରଣର ମୂଳଦ୍ଵୟ α ଓ ß।
ମୂଳଦ୍ବୟର ସମଷ୍ଟି = α + ß = \(\frac{-(-3)}{5}\) = \(\frac{3}{5}\), ମୂଳଦ୍ବୟର ଗୁଣଫଲ = αß = \(\frac{-2}{5}\)
∴ α³ + ß³ = (α + ẞ)³ – 3αß (α + B)
= (\(\frac{3}{5}\))³ – 3(\(\frac{3}{5}\))(\(\frac{-2}{5}\)) = \(\frac{27}{125}+\frac{18}{25}\) = \(\frac{27+90}{125}\) = \(\frac{117}{125}\)
∴ α³ + ß³ = \(\frac{117}{125}\) (ପ୍ରମାଣିତ)
![]()
Question 12.
ଯଦି 5x² + 17x + 6 = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ α ଓ ß ହୁଏ ତେବେ \(\frac{1}{α²}+\frac{1}{ß²}\) ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ :
5x² + 17x + 6 = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ α ଓ ß।
∴ ମୂଳଦ୍ବୟର ସମଷ୍ଟି = α + ß = \(\frac{-17}{5}\), ମୂଳଦ୍ବୟର ଗୁଣଫଲ = αß = \(\frac{6}{5}\)
\(\frac{1}{α²}+\frac{1}{ß²}\) = \(\frac{ß²+α²}{α²ß²}\) = \(\frac{(α+ß)²-2αẞ}{(αß)²}\)
=\(\frac{\left(\frac{-17}{5}\right)^2-2\left(\frac{6}{5}\right)}{\left(\frac{6}{5}\right)^2}=\frac{\frac{289}{25}-\frac{12}{5}}{\frac{36}{25}}\) = \(\frac{289-60}{25}\) × \(\frac{25}{36}\) = \(\frac{229}{36}\)
∴ \(\frac{1}{α²}+\frac{1}{ß²}\) ର ମୂଲ୍ୟ \(\frac{229}{36}\) ।
Question 13.
x² – 8x + 16p = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ α ଓ ß ହେଲେ \(\frac{αß}{α + ß}\) ପରିପ୍ରକାଶକୁ p ମାଧ୍ୟମରେ ପ୍ରକାଶ କର ।
ସମାଧାନ :
x² – 8x + 16p = 0 ମୂଳ ଦ୍ଵୟ α ଓ ß।
∴ ମୂଳଦ୍ବୟର ସମଷ୍ଟି = α + ß = \(\frac{-(-8)}{1}=8\), ମୂଳଦ୍ବୟର ଗୁଣଫଲ = αß = \(\frac{16p}{1}=16p\)
∴ \(\frac{αß}{α + ß}\) = \(\frac{16p}{8}\) = 2p
Question 14.
ଯଦି x² – 2 (5 + 2m) x + 3 (7 + 10m) = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ ଏକ ଓ ଅଭିନ୍ନ ହୁଏ, m ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ :
x² – 2 (5 + 2m) x + 3 (7 + 10m) = 0 ସମୀକରଣର ମୂଳଦ୍ବୟ ଏକ ଓ ଅଭିନ୍ନ ।
ପ୍ରଭେଦକ (D) = 0
ଏଠାରେ a = 1, b = – 2 (5+ 2m), c = 3 (7 + 10m)
D = b² – 4ac = 0
⇒ {-2(5+ 2m)}² – 4 × 1 × 3 (7 + 10m) = 0
⇒ 4 (25 + 20m + 4m²) – 4 × 3 (7 + 10m) = 0
⇒ 100+ 80m + 16m² – 12 (7 + 10m) = 0
⇒ 16m² + 80m + 100 – 84 – 120m = 0 16m² – 40m + 16 = 0 ⇒ 2m² – 5m+2=0 2m² – 4m – m + 2=0
⇒ 2m (m – 2) – 1 (m – 2) = 0 ⇒ (m – 2) (2m – 1) = 0
m – 2 = 0 | 2m – 10 ⇒ m = 2 | m =
∴ m ର ମାନ 2 କିମ୍ବା \(\frac{1}{2}\) ହେଲେ x² – 2 (5 + 2m) x + 3 (7 + 10m) = 0 ସମୀକରଣର ମୂଳଦ୍ବୟ ଏକ ଓ ଅଭିନ୍ନ ହେବେ ।
Question 15.
(i) ଯଦି a = b = c ହୁଏ, ତେବେ ପ୍ରମାଣ କର ଯେ, ସମୀକରଣ
(x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) = 0 ର ମୂଳଦ୍ୱୟ ବାସ୍ତବ ଏବଂ ଏକ ଓ ଅଭିନ୍ନ ।
(ii) ଯଦି a + b + c = 0 ଏବଂ a, b, c ∈ Q ହୁଏ, ତେବେ ପ୍ରମାଣ କର ଯେ
(b + c – a) x² + (c + a – b) x + (a + b – c) = 0 ସମୀକରଣର ପରିମେୟ ହେବେ ।
ସମାଧାନ :
(i) a = b = c ହେଲେ, (x – a) (x – b) + (x – b) (x – c) + (x – c) (x – a) = 0
⇒ (x – a)² + (x – a)² + (x – a)² = 0
⇒ 3 (x – a)² = 0 ⇒ (x – a)² = 0 ⇒ x² – 2ax + a² = 0
ଏଠାରେ ପ୍ରଭେଦକ (D) = b² – 4ac = (-2a)² – 4(1) a² = 4a² – 4a² = 0
∴ D = 0 ହେଲେ, ମୂଳଦ୍ୱୟ ବାସ୍ତବ ଏବଂ ଏକ ଓ ଅଭିନ୍ନ ।
(ii) ଯଦି a+b+c=0, a, b, c ∈ Q
(b + c – a) x² + (c + a – b) x + (a + b – c) = 0
a + b + c = 0
⇒ b + c = a, c + a = – b, a + b = -c
(b + c – a) x² + (c + a – b) x + (a + b – c) = 0
⇒ -2ax² + (-2b) x + (- 2c) = 0 ⇒ 2 (ax² + bx + c) = 0
⇒ ax² + bx + c = 0
ପ୍ରଭେଦକ (D) = b² – 4ac = (-b)² – 4ac = (a + c)² – 4ac = (a – c)²
Question 16.
ଗୋଟିଏ ଦ୍ଵିଘାତ ସମୀକରଣର ମୂଳଦ୍ଵୟର ସମଷ୍ଟି 3 ଓ ମୂଳଦ୍ବୟର ବର୍ଗର ସମଷ୍ଟି 29 ହେଲେ, ସମୀକରଣଟି ନିରୂପଣ କର ।
ସମାଧାନ :
ମନେକର ସ୍ଵିଘାତ ସମୀକରଣର ମୂଳଦ୍ଵୟ α ଓ ß ।
ମୂଳଦ୍ବୟର ସମଷ୍ଟି = α + ß = 3
ମୂଳଦ୍ଵୟର ବର୍ଗର ସମଷ୍ଟି = α² + ß² = 29
⇒ (α + ß)² – 2 aẞ = 29 ⇒ 3² – 2αß = 29
⇒9 – 2αẞ = 29 ⇒ – 2αß = 29 – 9 = 20
αß = \(\frac{-20}{2}\) = -10
ସମୀକରଣଟି x² – (a + ẞ) x + αß = 0
⇒ x² – 3x + (-10) = 0 ⇒ x² – 3x – 10 = 0
Question 17.
ଯଦି 2x² – 4x + 2 = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ α ଓ ß ହୁଏ, ତେବେ ପ୍ରମାଣ କର ଯେ \(\frac{α}{ß}+\frac{ß}{α}\) + 4(\(\frac{1}{α}+\frac{1}{ß}\)) + 2αß = 12
ସମାଧାନ :
2x² – 4x + 2 = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ α ଓ ß ।
∴ ମୂଳଦ୍ଵୟର ସମଷ୍ଟି α + ß = \(\frac{-(-4)}{2}\) = -2 ଏବଂ ମୂଳଦ୍ଵୟର ଗୁଣଫଲ αβ = \(\frac{2}{2}\) = 1
L.H.S. = \(\frac{α}{ß}+\frac{ß}{α}\) + 63(\(\frac{1}{α}+\frac{1}{ß}\)) – 2αß
= \(\frac{ß²+α²}{αß}\) + 63\(\frac{(α+ß)}{(αß)}\) – 2αß
= \(\frac{(α+ß)²-2αß}{(αß)}\) + 4\(\frac{(α+ß)}{(αß)}\) + 2αß
= \(\frac{(2)²-2×1}{1}\) + \(\frac{4(2)}{1}\) + 2 × 1
= 2 + 8 + 2 = 12 = R.H.S.
![]()
Question 18.
(i) ଯଦି ax² + bx + c = 0 ସମୀକରଣର ଗୋଟିଏ ମୂଳ ଅପରଟିର 4 ଗୁଣ ହୁଏ, ତେବେ ପ୍ରମାଣ କର ଯେ 4b² = 25ac।
(ii) ଯଦି x² – px + q = 0 ସମୀକରଣର ଗୋଟିଏ ମୂଳ ଅପରଟିର 2 ଗୁଣ ହୁଏ, ତେବେ ପ୍ରମାଣ କର ଯେ 2p² = 9q ।
ସମାଧାନ :
(i) ମନେକର ax² + bx + c = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ α ଏବଂ 4α।
∴ ମୂଳଦ୍ଵୟର ସମଷ୍ଟି α + 4α = \(\frac{-b}{a}\) ⇒ 5α = \(\frac{-b}{a}\) ⇒ α= \(\frac{-b}{5a}\) .. (i)
ମୂଳଦ୍ଵୟର ଗୁଣଫଲ α.4α = \(\frac{c}{2}\)
⇒ \(4 α^2=\frac{c}{a} \Rightarrow 4 \times (\frac{-b}{5a})^2=\frac{c}{a}\) [(i)]
⇒ \(\frac{4b²}{25a²}=\frac{c}{a} \Rightarrow 4ab²=25a²c \Rightarrow 4b²=25 ac\) (ପ୍ରମାଣିତ)
(ii) ମନେକର x² – px + q = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ α ଏବଂ 2α।
∴ ମୂଳଦ୍ଵୟର ସମଷ୍ଟି α + 2α = \(\frac{-(-p)}{1}\) ⇒ 3α = p ⇒ α= \(\frac{p}{3}\) .. (i)
ମୂଳଦ୍ଵୟର ଗୁଣଫଲ α.2α = \(\frac{q}{1}\) = 2α² = q
⇒ 2 × (\(\frac{p}{3}\))³ = q ⇒ \(\frac{2p²}{3}\) = q ⇒ 2p² = 9q (ପ୍ରମାଣିତ)
Question 19.
(i) ଯଦି 41x² – 2 (5a + 4b) x + (a² + b²) = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ ସମାନ ହୁଅନ୍ତି, ତେବେ ପ୍ରମାଣ କର ଯେ, \(\frac{a}{b}=\frac{5}{4}\)।
(ii) ଯଦି x² + px + q = 0 ସମୀକରଣର ବୀଜଦ୍ଵୟର ସମଷ୍ଟି ସେମାନଙ୍କର ବର୍ଗର ସମଷ୍ଟି ସହ ସମାନ ଯେ, 2q = p (p + 1)।
(ii) ଯଦି x² + px + q = 0 ସମୀକରଣର ଗୋଟିଏ ବୀଜ ଅନ୍ୟଟିର ବର୍ଗ ହୁଏ, ତେବେ ଦର୍ଶାଅ ଯେ p³ + q² + q = 3pq।
ସମାଧାନ :
(i) 41x² – 2 (5a + 4b) x + (a² + b²) = 0 ସମୀକରଣର ମୂଳଦ୍ଵୟ ସମାନ।
ଏଠାରେ a = 41, b = -2(5a + 4b), c = (a² + b²)
ପ୍ରଭେଦକ (D) = b² – 4ac = 0
⇒ {-2 (5a + 4b)}² – 4 (41) (a² + b²) = 0
⇒ 4 (25a² + 40ab + 16b²) – 4 (41a² + 41b²) = 0
⇒(25a² + 40ab + 16b² – 41a² – 41b²) = 0
⇒(-16a² + 40ab – 25b²) = 0
⇒(16a² – 40ab + 25b²) = 0
⇒(4a)² – 2.4a.5b + (5b)² = 0
⇒ (4a – 5b)² = 0
⇒4a – 5b = 0 [∴ a² – 2ab + b² = (a – b)²]
⇒ 4a = 5b ⇒ \(\frac{a}{b}=\frac{5}{4}\)।
(ii) x² + px + q = 0 ସମୀକରଣର ବୀଜଦ୍ଵୟର ସମଷ୍ଟି ସେମାନଙ୍କର ବର୍ଗର ସମଷ୍ଟି ସହ ସମାନ ।
ମନେକର ସମୀକରଣର ବୀଜଦ୍ଵୟ α ଓ ß।
ବୀଜଦ୍ୱୟର ସମଷ୍ଟି α + ß = – p ଏବଂ ବୀଜଦ୍ବୟର ଗୁଣଫଳ αß = q
କିନ୍ତୁ ଦତ୍ତ ଅଛି α + ß = α² + ß²
⇒ α + ß = α² + ß² – 2αß ⇒ – p = (- p)² – 2q
⇒ 2q = p² + p ⇒ 2q = p (p + 1) (ପ୍ରମାଣିତ)
(iii) x + px + g = 0 ସମୀକରଣର ଗୋଟିଏ ବୀଜ ଅପରଟିର ବର୍ଗ ।
ମନେକର ସମୀକରଣର ବୀଜଦ୍ଵୟ α ଓ α²।
ବୀଜଦ୍ୱୟର ସମଷ୍ଟି α + α² = – p
ବୀଜଦ୍ବୟର ଗୁଣଫଳ α.α² = q ⇒ α³ = q
α + α² = – p = (α + α²)³ = -p³
⇒ a³ + α6 + 3α · a² (α + α²) = – p³ ⇒ q + q² + 3q (- p) = – p³
⇒ q² + q – 3pq = -p³ ⇒ p³ + q² + q = 3pq (ପ୍ରମାଣିତ)
![]()
Question 20.
ଯଦି a(b – c) x² + b(c – a) x + c (a – b) = 0 ସମୀକରଣର ବୀଜଦ୍ଵୟ ସମାନ ହୁଏ, ତେବେ ଦର୍ଶାଅ ଯେ, \(\frac{2}{b}=\frac{1}{a}+\frac{1}{c}\)
ସମାଧାନ :
a(b – c) x² + b(c – a) x + c (a – b) = 0 ସମୀକରଣର ବୀଜଦ୍ଵୟ ସମାନ ।
ସମୀକରଣର ପ୍ରଭଦେକ (D) = 0
⇒ {b (c – a)}² – 4a (bc) c (a – b) = 0
⇒ b² (ca)² – 4a (b -c) c (a – b) = 0
⇒(bc – ab)² – 4 a(b – c) · c (a – b) = 0
⇒ (ab – ca + ca – bc)² – 4a (b- c) · c (a – b) = 0
⇒ {a (b-c) + c (a – b)}² – 4a (b – c) c (a – b) = 0
⇒ {a (bc) -c (a – b)}² = 0 ⇒ (ab – ac- ca + bc) = 0
⇒ ab + bc = 2 ca ⇒ \(\frac{ab}{abc}+\frac{bc}{abc}=\frac{2ca}{abc}\) (abc ଦ୍ବାରା ଉଭୟ ପାର୍ଶ୍ଵକୁ ଭାଗ କଲେ)
⇒ \(\frac{1}{c}+\frac{1}{a}=\frac{2}{b}\) (ପ୍ରମାଣିତ)
