CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Ex 8(c)

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Ex 8(c) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Exercise 8(c)

Question 1.
Find the intervals where the following functions are (a) increasing and (b) decreasing.
(i) y = sin x, x ∈ [0, 2π]
Solution:

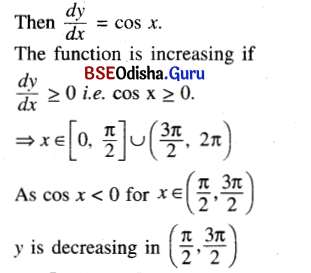
(ii) y = In x, x ∈ R₊
Solution:
⇒ \(\frac{d y}{d x}\) = \(\frac{1}{x}\) > 0
for all x ∈ R₊.
Thus y = In x is increasing in (0, ∞) and decreasing nowhere.

(iii) y = a^x, a > 0, x ∈ R
Solution:
⇒ \(\frac{d y}{d x}\) = a^x In a > 0 for all x ∈ R provided a > 1.
The function is increasing in (-∞, ∞) is a > 1.
Again \(\frac{d y}{d x}\) = a^x In a < 0 if 0 < a < 1.
Thus the function is decreasing in (-∞, ∞) if (0 < a < 1)

(iv) y = sin x + cos x, x ∈ [0, 2π]
Solution:

(v) y = 2x³ + 3x² – 36x – 7
Solution:
\(\frac{d y}{d x}\) = 6x² – 6x – 36
y is increasing if \(\frac{d y}{d x}\) > 0
⇒ x² + x – 6>0
⇒ x² + 3x – 2x – 6>0
⇒ x (x + 3) -2 (x + 3) > 0
⇒ (x + 3) (x – 2) > 0
for x > 2 or x < -3 and (x + 3 ) (x – 2) < 0 for -3 < x < 2
∴ The function is increasing in (-∞, -3) ∪ (2, ∞) and is decreasing in (-3, 2).

(vi) y = \(\frac{1}{x-1^{\prime}}\) x ≠ 1
Solution:
\(\frac{d y}{d x}\) = \(\frac{-1}{(x-1)^2}\)
The function is increasing if \(\frac{d y}{d x}\) > 0
⇒ \(\frac{-1}{(x-1)^2}\) > 0 which is impossible because \(\frac{-1}{(x-1)^2}\) is always -ve for all x ≠ 1. So the function is increasing nowhere. It is decreasing in R – {1}

(vii) y = \(\left\{\begin{array}{cc}
x^2+1, & x \leq-3 \\
x^3-8 x+13, & x>-3
\end{array}\right.\)
Solution:

(viii) y = 4x² + \(\frac{1}{x}\)
Solution:

(ix) y = (x – 1)² (x + 2)
Solution:
\(\frac{d y}{d x}\) = 2 (x – 1) (x + 2) + (x – 1)²
= (x – 1) (2x + 4 + x – 1)
= (x – 1 ) (3x + 3)
= 3 (x – 1) (x + 1 )
The function is increasing if \(\frac{d y}{d x}\) > 0.
⇒ (x + 1) (x – 1) > 0
⇒ x < -1 or x > 1
∴ The function is increasing in (-∞, -1) ∪ (1, ∞)
It is decreasing in (-1, 1).

(x) y = \(\frac{\ln x}{x}\), x > 0
Solution:

(xi) y = tan x – 4 (x – 2), x ∈ (-\(\frac{\pi}{2}\), \(\frac{\pi}{2}\))
Solution:

(xii) y = sin 2x – cos 2x, x ∈ [0, 2π]
Solution:

Question 2.
Give a rough sketch of the functions given in question 1.
Solution:
Do yourself.

Question 3.
Show that the function \(\frac{e^x}{x^p}\) is strictly increasing for x > p > 0.
Solution:

Question 4.
Show that 2 sin x + tan x ≥ 3x for all x ∈ (0, \(\frac{\pi}{2}\)).
Solution:
Let f(x) = 2 sin x + tan x – 3x
Then f(x) = 2 cos x + sec² x – 3