CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Additional Exercise

Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 9 Integration Additional Exercise Textbook Exercise questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Additional Exercise

Question 1.
∫\(\sqrt{1-\sin 2 x}\) dx
Solution:
I = ∫\(\sqrt{1-\sin 2 x}\) dx
= ∫\(\sqrt{(\cos x-\sin x)^2}\) dx
= ∫(cos x – sin x) dx
= sin x + cos x + c

Question 2.
∫\(\frac{d x}{1+\sin x}\)
Solution:
I = ∫\(\frac{d x}{1+\sin x}\)
= ∫\(\frac{1-\sin x}{\cos ^2 x}\)
= ∫sec² x – sec x tan x dx
= tan x – sec x + c

Question 3.
∫\(\frac{\sin x}{1+\sin x}\) dx
Solution:

Question 4.
∫\(\frac{\sec x}{\sec x+\tan x}\) dx
Solution:
I = ∫\(\frac{\sec x}{\sec x+\tan x}\) dx
= ∫\(\frac{\sec x(\sec x-\tan x)}{\sec ^2 x-\tan ^2 x}\) dx
= ∫sec² x – sec x tan x dx
= tan x – sec x + c

Question 5.
∫\(\frac{1+\sin x}{1-\sin x}\) dx
Solution:
I = ∫\(\frac{1+\sin x}{1-\sin x}\) dx
= ∫\(\frac{(1+\sin x)^2}{\cos ^2 x}\) dx
= ∫[sec² x+ tan² x+ 2sec x tan x) dx
= ∫[2sec² x – 1 + 2sec x tan x) dx
= 2tan x – x + 2sec x + c

Question 6.
∫tan^-1 (sec x + tan x) dx
Solution:

Question 7.
∫\(\frac{\cos 2 x-\cos 2 \alpha}{\cos x-\cos \alpha}\) dx
Solution:
I = ∫\(\frac{\cos 2 x-\cos 2 \alpha}{\cos x-\cos \alpha}\) dx
= ∫\(\frac{\left(2 \cos ^2 x-1\right)-\left(2 \cos ^2 \alpha-1\right)}{\cos x-\cos \alpha}\) dx
= 2 ∫(cos x + cos α) dx
= 2 sin x + 2x cos α + c

Question 8.
∫tan-1\(\sqrt{\frac{1-\cos 2 x}{1+\cos 2 x}}\) dx
Solution:

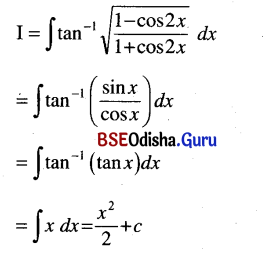
Question 9.
∫\(\frac{d x}{\sqrt{x+1+} \sqrt{x+2}}\)
Solution:

Question 10.
∫\(\frac{2+3 x}{3-2 x}\) dx
Solution:

Question 11.
∫\(\frac{d x}{\sqrt{x}+x}\)
Solution:

Question 12.
∫\(\frac{d x}{1+\tan x}\)
Solution:

Question 13.
∫\(\frac{x+\sqrt{x+1}}{x+2}\) dx (Hints put : \(\sqrt{x+1}\) = t)
Solution:

Question 14.
∫sin^-1\(\sqrt{\frac{x}{a+x}}\) dx (Hints put : x = a tan² t)
Solution:

Question 15.
∫e^x\(\left(\frac{2+\sin 2 x}{1+\cos 2 x}\right)\) dx
Solution:

Question 16.
∫\(\frac{\left(x^2+1\right) e^x}{(x+1)^2}\) dx
Solution:

Question 17.
∫\(\frac{x^2-1}{x^4+x^2+1}\) dx
Solution:

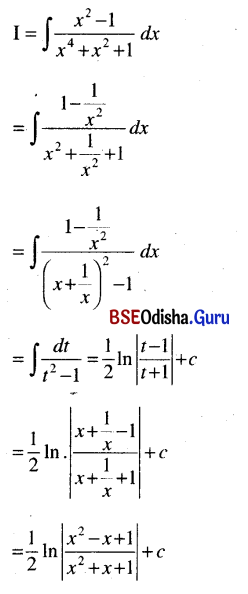
Question 18.
∫\(\frac{x^2 d x}{x^4+x^2+1}\)
Solution:

Question 19.
∫\(\sqrt{\cot x}\) dx
Solution:

Question 20.
∫\((\sqrt{\tan x}+\sqrt{\cot x})\) dx
Solution:

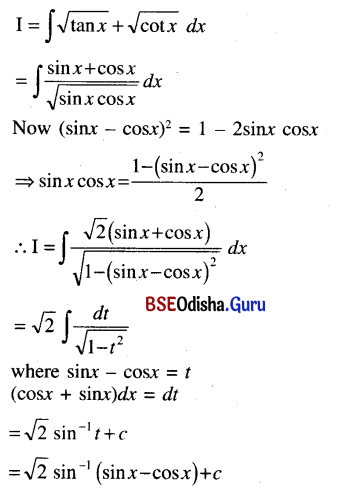
Question 21.
∫\(\frac{\mathrm{dx}}{x\left(x^4+1\right)}\)
Solution:

Question 22.
∫\(\frac{\mathrm{dx}}{e^x-1}\)
Solution:

Question 23.
∫\(\frac{(x-1)(x-2)(x-3)}{(x+4)(x-5)(x-6)}\) dx
Solution:

Question 24.
∫\(\frac{d x}{\left(e^x-1\right)^2}\)
Solution:

Question 25.
∫\(\frac{d x}{\sin x \cos ^2 x}\)
Solution:

Question 26.
\(\int_2^4 \frac{\left(x^2+x\right) d x}{\sqrt{2 x+1}}\)
Solution:

Question 27.
\(\int_{-a}^a \sqrt{\frac{a-x}{a+x}}\) dx
Solution:

Let a² – x² = t²
-2x dx = 2t dt
x = -a ⇒ 0 t = 0
x = a ⇒ t = 0
= 0
I = aI₁ – I₂ = aπ

Question 28.
\(\int_0^{\pi / 2}(\sqrt{\tan x}+\sqrt{\cot x})\) dx
Solution:

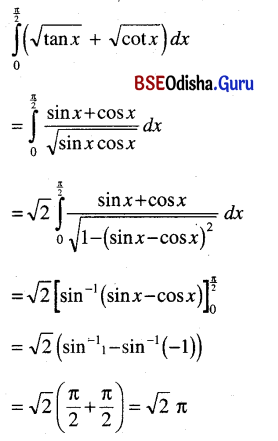
Question 29.
\(\int_0^{\pi / 2} \frac{\cos x d x}{1+\cos x+\sin x}\)
Solution:

Question 30.
\(\int_0^1\)x (1 – x)ⁿ dx
Solution:

Question 31.
\(\int_0^{\pi / 2}\)sin 2x log (tan x) dx
Solution:

Question 32.
\(\int_0^{\pi / 2} \frac{\sin ^2 x d x}{\sin x+\cos x}\)
Solution:

Question 33.
\(\int_0^{\pi / 2} \frac{\sin ^2 x d x}{1+\sin x \cos x}\)
Solution:

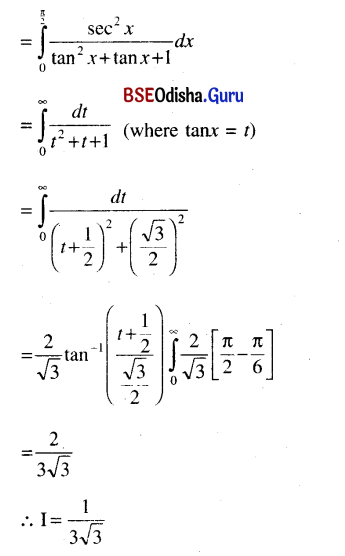
Question 34.
\(\int_0^{\pi / 2} \frac{x d x}{\sin x+\cos x}\)
Solution:

Question 35.
Prove that \(\int_0^\pi\) x sin³ x dx = \(\frac{2 \pi}{3}\)
Solution:

Question 36.
\(\int_{\pi / 5}^{3 \pi / 10} \frac{\sin x d x}{\sin x+\cos x}\)
Solution:

Question 37.
\(\int_0^\pi\)|cos x| dx
Solution:

Question 38.
\(\int_1^4\)(|x – 1| + |x – 2| + |x – 3|) dx
Solution:

Question 39.
\(\int_{-\pi / 2}^{\pi / 2}\)(sin |x| + cos |x|) dx
Solution:

Question 40.
\(\int_0^\pi\)log (1 + cos x) dx
Solution: