CHSE Odisha Class 12 Math Solutions Chapter 10 Area Under Plane Curves Ex 10

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 10 Area Under Plane Curves Ex 10 Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 10 Area Under Plane Curves Exercise 10

Question 1.
Find the area bounded by
(i) y = e^x, y = 0, x = 4, x = 2
Solution:
Area = \(\int_2^4\)e^x dx
= \(\left[e^x\right]_2^4\)
= e⁴ – e²

(ii) y = x², y = 0, x = 1
Solution:
Area = \(\int_0^1\)x² dx
= \(\left[\frac{x^3}{3}\right]_0^1\)
= \(\frac{1}{3}\)

(iii) xy = a², y = 0, x = α, x = β (β > α > 0)
Solution:
Area = \(\int_\alpha^\beta y\)y dx
= \(\int_\alpha^\beta \frac{a^2}{x}\) dx
= a²\([\ln x]_\alpha^\beta\)
= a² ln (β/α)

(iv) y = sin x, y = 0, x = \(\frac{\pi}{2}\)
Solution:
Area = \(\int_0^{\frac{\pi}{2}}\)sin x dx
= \([-\cos x]_0^{\frac{\pi}{2}}\)
= -cos\(\frac{\pi}{2}\) + cos θ = 1

Question 2.
Find the area enclosed by
(i) y = e^x, x = 0, y = 2, y = 3
Solution:

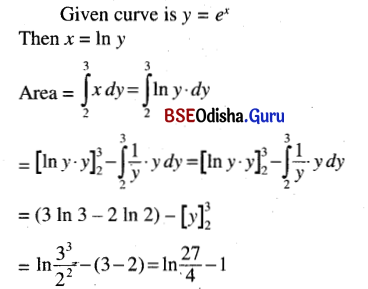
(ii) y² = x, x = 0, y = 1
Solution:
Area = \(\int_0^1\)x dy
= \(\int_0^1\)y² dy
= \(\left[\frac{y^3}{3}\right]_0^1\)
= \(\frac{1}{3}\)

(iii) xy = a², x = 0, y = α, y = β (β > α > 0)
Solution:
Area = \(\int_\alpha^\beta\)x dy
= \(\int_\alpha^\beta \frac{a^2}{y}\)dy
= a²\([\ln y]_\alpha^\beta\)
= a² ln (β/α)

(iv) y² = x³, x = 0, y = 1
Solution:
Given curve is y² = x³
⇒ x = y^2/3
It passes through the origin. So the required area
= \(\int_0^1\)x dy
= \(\int_0^1 y^{\frac{2}{3}}\) dy
= \(\left[\frac{y^{\frac{5}{3}}}{5 / 3}\right]_0^1\)
= \(\frac{3}{5}\)

Question 3.
(i) Determineellipse the area with in the ellipse
\(\frac{x^2}{a^2}\) + \(\frac{y^2}{b^2}\) = 1
Solution:

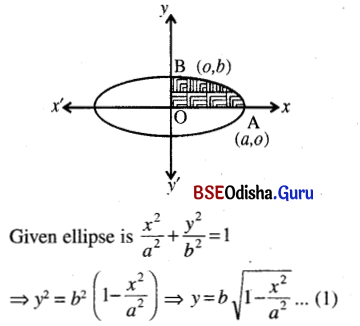
The ellipse is symmetrical about x-axis and y-axis.It is divided into 4 equal parts by the coordinate axes. So required area

(ii) Find the area of the circle x² + y² = 2ax.
Solution:
Given circle is x² + y² = 2ax
⇒ x² – 2ax + a² + y² = a²
⇒ (x – a)² + y² = a² … (1)
The centre of the circle is (a, 0) and radius is a.

(iii) Find the area of the portion of the parabola y² = 4x bounded by the double ordinate through (3, 0).
Solution:
Given parabola is y² = 4x

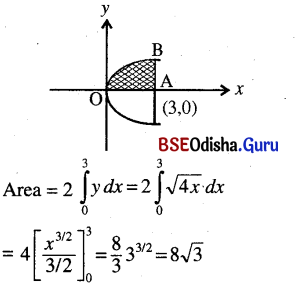
(iv) Determine the area of the region bounded by y² = x³ and the double ordinate through (2, 0)
Solution:
Given curve is y² = x³
⇒ y = ±x^3/2 … (1)
The curve passes through the origin and symmetrical about x-axis because the power of y is even.

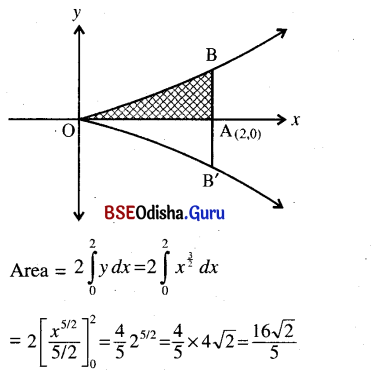
Question 4.
(i) Find the area of the regions into which the circle x² + y² = 4 is divided by the line x + √3y = 2.
Solution:
Given circle and the straight line are x²+ y² = 4 and x+ √3y = 2
The circle has the centre at (0, 0) and radius ‘2’.
The eqn. (2) can be written as
y = –\(\frac{1}{\sqrt{3}}\)x + \(\frac{2}{\sqrt{3}}\)
Slope of the strainght line = –\(\frac{1}{\sqrt{3}}\)
The line makes and angle of 150° with x-axis making intercept \(\frac{2}{\sqrt{3}}\) from y-axis.
It intersects x-axis at (2, 0).

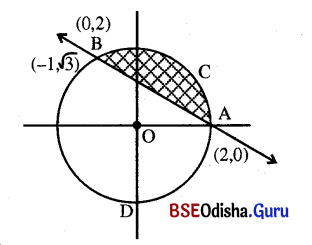
Solveing (1) and (2),
ge wet (2 – 3√y)² + y² = 4
4 + 3√y² – 4√3y + y² = 4
4y² – 4√3y = 0
y(y – √3) = 0
y = 0 or y = √3
When y = 0, x = 2
When y = √3, x = -1
Thus the straight line intersects the circle at (2, 0) and (-1, √3).
Area of the portion ACBA.

(ii) Determine the area of the region between the curves y = cos x and y = sin x, bounded by x = 0.
Solution:

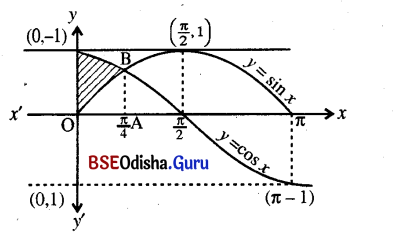
The curves y = cos x and y = sin x are shown in the above figure. The region included between these two curves in [0, \(\frac{\pi}{4}\)] is OABO.

(iii) Find the area enclosed by the two parabolas y² = 4 ax and x² = 4ay.
Solution:
The given parabolas are y² = 4ax and x² = 4ay.
The graphs of the two parabolas are shown in the figure.

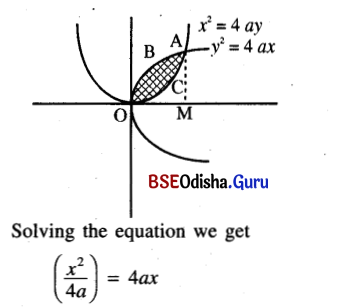
⇒ x⁴ = 64 a⁴
⇒ x⁴ – 64 a³x = 0
⇒ x (x³ – (4a)³) = 0
⇒ x (x – 4a) (x² + 4ax + 16a²) = 0
⇒ x = 0, 4a
When x = 0, y = 0 and
when x = 4a, y = 4a
Thus the two parabolas intersect at (0, 0) and (4a, 4a).
Area between two parabolas

(iv) Determine the area common to the parabola y² = x and the circle x²+ y² = 2x.
Solution:
Gien parabola is y² = x
Given circle is
x² + y² = 2x ⇒ (x – 1)² + y² = 1
The centre is at (1, 0) and radius is 1.

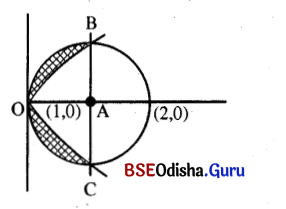
Solving (1) and (2) we get
x² + x = 2x ⇒ x² – x = 0 ⇒ x(x – 1) = 0
⇒ x = 0, x = 1
When x = 0, y = 0 and when x = 1, y = 1.
Thus both the parabola and circle intersect at (0, 0) and (1, 1).
Required Area