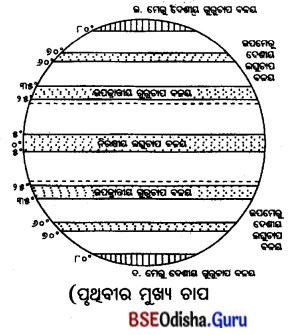
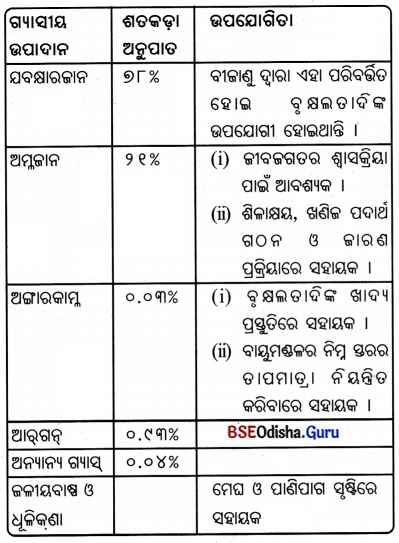
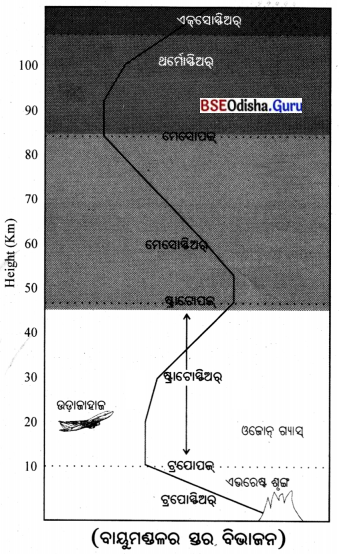
Odisha State Board BSE Odisha 8th Class Geography Important Questions Chapter 3.1 କୃଷି Important Questions and Answers.
BE Odisha Class 8 Geography Important Questions Chapter 3.1 କୃଷି
Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
Question 1.
ସଘନ ପ୍ରୟୋଜନଭିତ୍ତିକ କୃଷି ବିଷୟରେ ସଂକ୍ଷେପର ଲେଖ ।
Answer:
- ଛୋଟ ଛୋଟ ଜମିରେ ଉନ୍ନତ ବିହନ, ନିୟମିତ ଜଳସେଚନ, ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାଣର ସାର ପ୍ରୟୋଗ କରି ଅଧ୍ବକ ଶ୍ରମିକ ଦ୍ଵାରା ଋଷ କରି ଅଧୂକ ଫସଲ ଉତ୍ପାଦନକୁ ସଘନ ପ୍ରୟୋଜନ ଭିଭିକ କୃଷି କୁହାଯାଏ।
- ଉର୍ବର ମ୍ପରିକା ଓ ଅନୁକୂଳ ଜଳବାୟୁରେ ଏକାଧିକ ଫସଲ ଉତ୍ପାଦନ ସମ୍ଭବ ହୁଏ ।
- ଧାନ, ଗହମ, ମକା, ଡାଲିଜାତୀୟ ଶସ୍ୟ, ତୈଳବୀଜ ଆଦି ଋଷ କରାଯାଏ ।
- ଭାରତର କୃଷକ ନିଜର ଋହିଦା ପୂରଣ କରିବାପାଇଁ ସଘନ ପ୍ରଣାଳୀରେ ବିଭିନ୍ନ ଶସ୍ୟ ଉତ୍ପାଦନ କରିଥାଏ।
- ଦକ୍ଷିଣ, ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଓ ପୂର୍ବ ଏସିଆର ମୌସୁମୀ ଅଞ୍ଚଳ, ପଶ୍ଚିମ ଇଉରୋପ ଓ ଭୂମଧ୍ଯସାଗରୀୟ ଅଞ୍ଚଳରେ ସଘନ କୃଷି କରାଯାଇ ଅଧିକ ଫସଲ ଉତ୍ପାଦନ କରାଯାଇଥାଏ। ଧାନ ଏହି ଅଞ୍ଚଳର ମୁଖ୍ୟ ଫସଲ ।
![]()
Question 2.
ମିଶ୍ରିତ କୃଷି ବିଷୟରେ ସଂକ୍ଷେପରେ ଲେଖ ।
Answer:
- ଖାଦ୍ୟଶସ୍ୟ, ପଶୁଖାଦ୍ୟ ଉତ୍ପାଦନ ସହ ପଶୁପାଳନକୁ ମିଶ୍ରିତ କୃଷି କୁହାଯାଏ ।
- ଏ ପ୍ରକାର କୃଷି ବିଶେଷତଃ କ୍ରାନ୍ତୀୟ ଜଳବାୟୁ ଅଞ୍ଚଳ; ଯଥା- ଏସିଆର ଥାଇଲାଣ୍ଡ, ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ପୂର୍ବଭାଗ, ଦକ୍ଷିଣ ଆଫ୍ରିକା, ନିଉଜିଲ୍ୟାଣ୍ଡ, ଅଷ୍ଟ୍ରେଲିଆର ଦକ୍ଷିଣ-ପୂର୍ବାଶ, ଇଉରୋପ ଓ ଦକ୍ଷିଣ ଆମେରିକାର ଆର୍ଜେଣ୍ଟିନାରେ କରାଯାଏ।
- ଏ ସବୁ ଅଞ୍ଚଳରେ ପଶୁମାନଙ୍କୁ ମକା, ଗହମ ଓ ଅନ୍ୟାନ୍ୟ ଖାଦ୍ୟ ଖୁଆଇ ହୃଷ୍ଟପୁଷ୍ଟ କରାଯାଇଥାଏ ।
- ଯାନ୍ତ୍ରିକ ଉପାୟରେ ପଶୁମାନଙ୍କଠାରୁ ଦୁଗ୍ଧ, ମାଂସ ଓ ଲୋମ ସଂଗ୍ରହ କରି ବିଦେଶକୁ ରପ୍ତାନି କରାଯାଏ ।
- ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ପଶୁଗରଣ ଭୂମିକୁ ‘ରାଞ୍ଚ’ କୁହାଯାଏ।
Question 3.
ଉଦ୍ୟାନ କୃଷି ବିଷୟରେ ସଂକ୍ଷେପରେ ଲେଖ ।
Answer:
- ସହର ଓ ବଡ଼ ବଡ଼ ନଗରରେ ବାସକରୁଥିବା ଲୋକମାନଙ୍କର ଆବଶ୍ୟକତା ପୂରଣ ପାଇଁ ତାହାର ଚତୁଃପାର୍ଶ୍ଵରେ ବିସ୍ତୃତ ଅଞ୍ଚଳରେ ପନିପରିବା ଓ ଫଳ ଫୁଲ ଇତ୍ୟାଦି ଋଷ କରାଯାଏ । ଏ ପ୍ରକାର କୃଷିକୁ ଉଦ୍ୟାନ କୃଷି କୁହାଯାଏ।
- ସ୍ଵଳ୍ପ ବୃଷ୍ଟିପାତ ଅଞ୍ଚଳରେ ଗ୍ରୀଷ୍ମ ଓ ଶୀତ ଋତୁରେ ପନିପରିବା ଋଷ କରାଯାଇଥାଏ ।
- ପନିପରିବା ସହ କଦଳୀ, ଆମ୍ବ, ପଣସ, ନଡ଼ିଆ ତଥା ଫୁଲ ଋଷ କରି ଋଷୀ ବିଶେଷ ଲାଭବାନ୍ ହୋଇଥାଏ । ଏହା ଏକ ଲାଭଜନକ କୃଷି ।
- ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ଉତ୍ତର-ପୂର୍ବଂଶ ଓ ଭାରତର ଉପକୂଳବର୍ତୀ ଅଞ୍ଚଳରେ ଏହି ଋଷ ବିଶେଷ ଭାବରେ କରାଯାଏ ।
- ବିଦେଶରେ ଭାରତର ଆମ୍ବ, ଓଡ଼ିଶାର ପାନ ଓ କେରଳର ନଡ଼ିଆ ବିଶେଷ ଋହିଦା ରହିଛି ଏବଂ ଏହା ବିଦେଶକୁ ରପ୍ତାନି କରାଯାଇଥାଏ ।
Question 4.
ଋହା ଋଷ ପାଇଁ କି ପ୍ରକାର ଜଳବାୟୁ, ମୃତ୍ତିକା, କେତେ ତାପମାତ୍ରା ଓ ବୃଷ୍ଟିପାତ ଆବଶ୍ୟକ ହୋଇଥାଏ ? ଭାରତର କେଉଁ ଅଞ୍ଚଳରେ ଏହି ଋଷ ବିଶେଷ ଭାବରେ କରାଯାଏ ?
Answer:
- ଗହା ଋଷ କ୍ରାନ୍ତୀୟ ଓ ଉପକ୍ରାନ୍ତୀୟ ଜଳବାୟୁ ଅଞ୍ଚଳରେ ବିଶେଷ ଭାବରେ କରାଯାଇଥାଏ । ଉଷ୍ମ ଓ ଆର୍ଦ୍ର ଜଳବାୟୁରେ ଋହା ଋଷ ଭଲ ହୁଏ ।
- ପାହାଡ଼ିଆ ଗଢ଼ାଣିଆ ଅଂଶରେ ଧାଡ଼ି ଧାଡ଼ି କରି ଗହା ଚାଷ କରାଯାଏ। ଗଛମୂଳରେ ପାଣି ଜମିଲେ ଗହା ଗଛ ନଷ୍ଟ ହୋଇଥାଏ ।
- ଋହା ଗଛର ଉପର କଅଁଳିଆ ପତ୍ରକୁ ଶୁଖାଇ ରହା ପ୍ରସ୍ତୁତ କରାଯାଏ। ।
- ଏହା ପାଇଁ ଅଧିକ ଶ୍ରମିକ ଆବଶ୍ୟକ ହୋଇଥାଏ ।
- ଭାରତର ଆସାମ, ପଶ୍ଚିମବଙ୍ଗର ଦାର୍ଜିଲିଂ, ଦକ୍ଷିଣ ଭାରତର ନୀଳଗିରି ଓ କେରଳରେ ଋହା ଋଷ କରାଯାଏ ।
Question 5.
ପ୍ରୟୋଜନଭିଭିକ କୃଷି ସମ୍ବନ୍ଧରେ ଆଲୋଚନା କର ।
Answer:
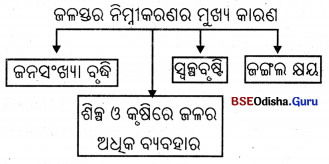
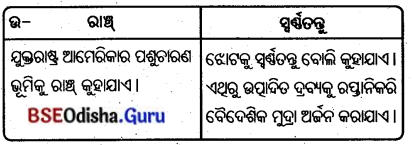
- ପ୍ରୟୋଜନ ଭିଭିକ କୃଷି ସାଧାରଣତଃ କୃଷକ ଓ ତା’ର ପରିବାରର ଦୈନନ୍ଦିନ ଖାଦ୍ୟ ଆବଶ୍ୟକତା ପୂରଣ କରିଥାଏ ।
- କୃଷକ ତା’ର ଛୋଟ ଜମିରେ ପାରମ୍ପରିକ ପୁରାତନ ପଦ୍ଧତିରେ ଚାଷ କାର୍ଯ୍ୟ କରିଥାଏ ।
- ଚାଷୀ ଗରିବ ହୋଇଥିବାରୁ ଜମିରେ ରାସାୟନିକ ସାର ଓ କୀଟନାଶକ ଦ୍ରବ୍ୟର ପ୍ରୟୋଗ, ଅଧିକ ଅମଳକ୍ଷମ ବିହନ ବ୍ୟବହାର କରିପାରେ ନାହିଁ ।
- ଜଳସେଚନର ଅଭାବ ହେତୁ ତା’ର ଜମିରେ ଉତ୍ପାଦନ କମ୍ ହୋଇଥାଏ ।
- ଭାରତ, ଚୀନ୍ ପ୍ରଭୃତି କେତେକ ବିକାଶୋନ୍ମୁଖୀ ଦେଶରେ ଏ ପ୍ରକାର କୃଷି ପଦ୍ଧତି ପ୍ରଚଳିତ ।
![]()
Question 6.
ପ୍ରୟୋଜନଭିଭିକ କୃଷି କେଉଁ କେଉଁ ପାରମ୍ପରିକ କୃଷି ପଦ୍ଧତିକୁ ବୁଝାଇଥାଏ ଲେଖ ।
Answer:
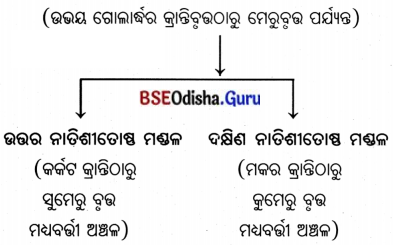
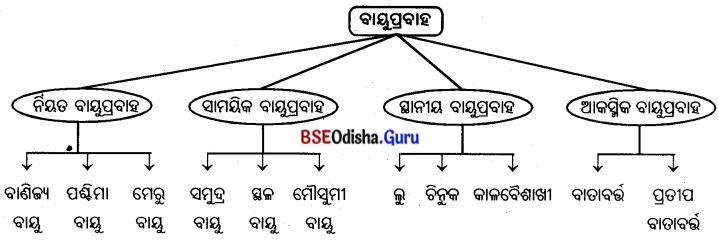
- ପ୍ରୟୋଜନଭିଭିକ କୃଷି ପଦ୍ଧତି ତିନୋଟି ପାରମ୍ପରିକ କୃଷି ପଦ୍ଧତିକୁ ବୁଝାଇଥାଏ, ଯଥା – ପଶୁବାରଣ, ସ୍ଥାନାନ୍ତରିତ କୃଷି ଓ ସଘନ ପ୍ରୟୋଜନଭିଭିକ କୃଷି ।
- ପଶୁ ଚାରଣ : ସାଧାରଣତଃ ଯାଯାବର ଶ୍ରେଣୀର ଲୋକମାନେ ମେଣ୍ଢା, ଛେଳି, ଗାଈ, ଓଟ, ଚମରୀଗାଈ ଆଦିକୁ ନେଇ ବିଭିନ୍ନ ତୃଣଭୂମି ଅଞ୍ଚଳରେ ବିଚରଣ କରନ୍ତି । ସେମାନେ ପଶୁମାନଙ୍କର ଚମଡ଼ା, ମାଂସ, ହାଡ଼, ଦୁଧ, ପଶମ ଇତ୍ୟାଦି ବିକି ପରିବାର ପୋଷଣ କରନ୍ତି ।
- ସ୍ଥାନାନ୍ତରିତ କୃଷି; ପାହାଡ଼ିଆ ବା ଜଙ୍ଗଲ ଅଞ୍ଚଳରେ ରହୁଥିବା ଅଧିବାସୀମାନେ ଜଙ୍ଗଲର ଏକ ଅଂଶ ସଫାକରି ପୋଡ଼ି ଦୁଇ ତିନି ବର୍ଷ ଚାଷ କରନ୍ତି । ଜମିର ଉର୍ବରତା କମିଗଲେ ଜଙ୍ଗଲର ଅନ୍ୟ ଏକ ଅଂଶରେ ସେହିପରି ପୋଡ଼ି ଚାଷ କାର୍ଯ୍ୟ କରନ୍ତି ।
- ସଘନ ପ୍ରୟୋଜନଭିଭିକ କୃଷି : ଏହି ପ୍ରକାର କୃଷିରେ ଛୋଟ ଛୋଟ ଜମିରେ ଉନ୍ନତ ବିହନ, ନିୟମିତ ଜଳସେଚନ, ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାଣର ସାର ପ୍ରୟୋଗରେ ଅଧିକ ଫସଲ ଉତ୍ପାଦନ ହୁଏ । ଧାନ, ମକା, ଗହମ, ଡାଲିଜାତୀୟ ଶସ୍ୟ, ତୈଳବୀଜ ଆଦି ଏହି ପ୍ରଣାଳୀରେ ଚାଷ କରାଯାଏ । ଦକ୍ଷିଣ, ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ, ପୂର୍ବ ଏସିଆର ମୌସୁମୀ ଅଞ୍ଚଳ, ପଶ୍ଚିମ ଇଉରୋପ ଓ ଭୂମଧ୍ଯସାଗରୀୟ ଅଞ୍ଚଳରେ ଏହି କୃଷି କରାଯାଏ ।
Question 7.
ବାଣିଜ୍ୟଭିତ୍ତିକ କୃଷିର ବିଶେଷତ୍ଵ ଲେଖ ।
Answer:
- କୃଷି ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟକୁ ବଜାରରେ ବିକ୍ରି କରିବା। ଏ ପ୍ରକାର କୃଷି ବ୍ୟବସ୍ଥାର ମୁଖ୍ୟ ଉଦ୍ଦେଶ୍ୟ ।
- ଦେଶର ଆବଶ୍ୟକତାକୁ ପୂରଣ କରିବା ସହ ବଳକା ଦ୍ରବ୍ୟକୁ ଅନ୍ୟ ଦେଶକୁ ରପ୍ତାନି କରାଯାଇ ଅର୍ଥ ଉପାର୍ଜନ କରାଯାଏ, ତେଣୁ ଏହାକୁ ମଧ୍ୟ ଅର୍ଥକରୀ କୃଷି କୁହାଯାଏ ।
- ବାଣିଜ୍ୟ ଉଦ୍ଦେଶ୍ୟରେ ଉନ୍ନତ ଦେଶ; ଯଥା – ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, କାନାଡ଼ା, ଇଉକ୍ରେନ୍, ରୁଷିଆ, ଆର୍ଜେଣ୍ଟିନା, ଅଷ୍ଟ୍ରେଲିଆ ପ୍ରଭୃତି ଦେଶରେ ଶସ୍ୟ ଉତ୍ପାଦନ ସହ ପଶୁପାଳନ, ମାଛଚାଷ, କୁକୁଡ଼ାଚାଷ, ରବର, ଚାହା, କଫି, ଫଳ, ପନିପରିବା ଚାଷ କରାଯାଏ ।
- ସାଧାରଣତଃ ଏହି କୃଷି କାର୍ଯ୍ୟ, ଯଥା – ଜମିଚାଷ କରିବା, ବିହନ ବୁଣିବା, ସାର ପ୍ରୟୋଗ କରିବା, କୀଟନାଶକ ଦ୍ରବ୍ୟ ସିଞ୍ଚନ, ଜମିରେ ପାଣି ମଡ଼ାଇବା, ଶସ୍ୟ ଅମଳ ଆଦି ଯାନ୍ତ୍ରିକ ଉପାୟରେ କରାଯାଏ ।
Question 8.
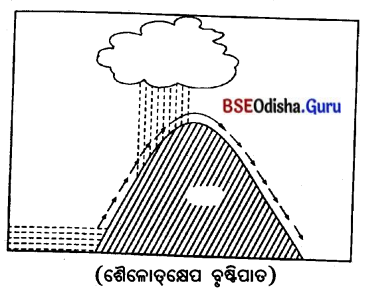
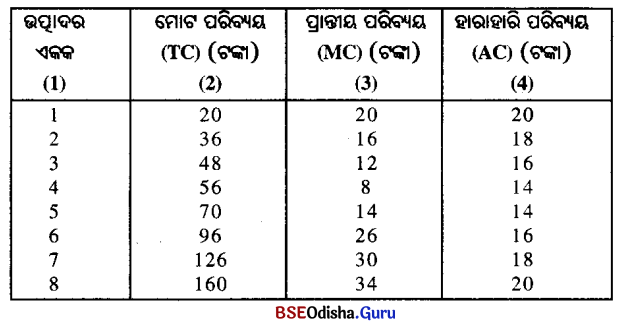
ଧାନଚାଷ ପାଇଁ ଆବଶ୍ୟକ ଭୌତିକ ନିବେଶଗୁଡ଼ିକ ଲେଖ ।
Answer:
ଧାନଚାଷ ପାଇଁ ଆବଶ୍ୟକୀୟ ଅନୁକୂଳ ଅବସ୍ଥାଗୁଡ଼ିକ ହେଲା–
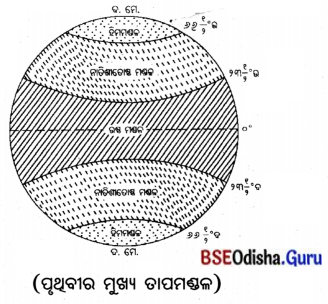
- କ୍ରାନ୍ତୀମଣ୍ଡଳରେ ଧାନଚାଷ କରାଯାଇଥାଏ ।
- ନଦୀ ଉପତ୍ୟକା ଓ ତ୍ରିକୋଣଭୂମି ଅଞ୍ଚଳର ମଟାଳ, ପଟୁ ଓ ଦୋରସା ମୃରିକାରେ ଅଧିକ ପରିମାଣରେ ଧାନ ଚାଷ କରାଯାଏ ।
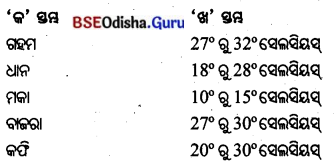
- ଧାନ ଚାଷପାଇଁ 27 ଡିଗ୍ରୀରୁ 30 ଡିଗ୍ରୀ ସେଲ୍ସିୟସ୍ ପର୍ଯ୍ୟନ୍ତ ତାପମାତ୍ରା ଆବଶ୍ୟକ ହୋଇଥାଏ ।
- 100ରୁ 200 ସେଣ୍ଟିମିଟର ବୃଷ୍ଟିପାତ ହେଉଥିବା ଅଞ୍ଚଳରେ ଧାନଚାଷ କରାଯାଏ ।
- ଧାନଚାଷ ଅଧିକ ଆର୍ଦ୍ରତା ଓ ତାପମାତ୍ରା ଆବଶ୍ୟକ କରିଥାଏ ।
![]()
Question 9.
ଭାରତରେ ଗହମ ଋଷ ସଂପର୍କରେ ଉଲ୍ଲେଖ କର ।
Answer:
- ଭାରତରେ ଗହମ ଏକ ରବି ଫସଲ ବା ଶୀତକାଳୀନ ଫସଲ ।
- ଭାରତରେ ଗଙ୍ଗା-ସତଜ ସମତଳ ଅଞ୍ଚଳ ମୁଖ୍ୟ ଗହମ ଉତ୍ପାଦନ ଅଞ୍ଚଳ । ପଞ୍ଜାବ, ହରିୟାଣା, ରାଜସ୍ଥାନ, ଉତ୍ତରପ୍ରଦେଶ ଏବଂ ମଧ୍ୟପ୍ରଦେଶରେ ଗହମ ଋଷ କରାଯାଏ ।
- 10 ରୁ 15 ସେଲ୍ସିୟସ୍ ତାପମାତ୍ରା ଏହି ଚାଷ ପାଇଁ ଉପଯୁକ୍ତ, ମାତ୍ର ଅମଳ ସମୟରେ 20 ରୁ 25° ସେଲ୍ସିୟସ୍ ତାପମାତ୍ରା ଆବଶ୍ୟକ ।
- ଗହମ ଉତ୍ପାଦନରେ ଭାରତ ବର୍ତ୍ତମାନ ଆତ୍ମନିର୍ଭରଶୀଳ।
- ଦେଶର ଋହିଦା ପୂରଣ କରିବା ସହିତ ବିଦେଶକୁ ଗହମ ରପ୍ତାନି କରିବାରେ ଆମ ଦେଶ ସକ୍ଷମ ହୋଇଛି ।
Question 10.
ଝୋଟଚାଷ ପାଇଁ ଅନୁକୂଳ ଅବସ୍ଥାମାନ ଉଲ୍ଲେଖ କରି ଏହି ଚାଷରେ ଅଗ୍ରଣୀ ଭାରତର ରାଜ୍ୟର ନାମ ଲେଖ । ଭାରତର ଏହି ଚାଷର ଆର୍ଥିକ ଗୁରୁତ୍ବ ଉଲ୍ଲେଖ କର ।
Answer:
- ଝୋଟଚାଷ ପାଇଁ ଉର୍ବର ପଟୁ ମୃରିକା, ଆର୍ଦ୍ର ଜଳବାୟୁ, ଅତ୍ୟଧିକ ବୃଷ୍ଟିପାତ ଅତ୍ୟନ୍ତ ଅନୁକୂଳ ।
- ବାଂଲାଦେଶ ଓ ଭାରତ ମୁଖ୍ୟ ଝୋଟ ଉତ୍ପାଦନକାରୀ ଦେଶ ।
- ଭାରତର ପଶ୍ଚିମବଙ୍ଗ, ଆସାମ, ଓଡ଼ିଶା ଓ ଉତ୍ତର ପ୍ରଦେଶରେ ଝୋଟଚାଷ ଭଲ ହୁଏ ।
- ଆର୍ଥିକ ଗୁରୁତ୍ଵ : ଭାରତରେ ତିଆରି ଝୋଟଜାତ ଦ୍ରବ୍ୟ ଦେଶ ବିଦେଶରେ ଆଦୃତ । ଭାରତ ଝୋଟରେ ତିଆରି ଅଖା, ସୁତୁଲି ଓ ଅନ୍ୟାନ୍ୟ ବ୍ୟବହାର ଉପଯୋଗୀ ଜିନିଷ ରପ୍ତାନି କରି ବୈଦେଶିକ ମୁଦ୍ରା ଅର୍ଜନ କରେ ।
Question 11.
ଚାହା ଚାଷ ପାଇଁ ଆବଶ୍ୟକ ଅନୁକୂଳ ଭୌତିକ ନିବେଶଗୁଡ଼ିକ ଲେଖା।
Answer:
- ଚାହାଚାଷ ସାଧାରଣତଃ ଉଷ୍ଣ ଓ ଆର୍ଦ୍ର ଜଳବାୟୁରେ କରାଯାଇଥାଏ ।
- ଚାହାଚାଷ ନିମନ୍ତେ ଉଚ୍ଚ ଗଡ଼ାଣିଆ ଭୂମି ଓ ନିଗିଡ଼ା ଉର୍ବର ମୁଭିକା ଆବଶ୍ୟକ ହୋଇଥାଏ ।
- 20 ରୁ 30° ସେଲ୍ସିୟସ୍ ମଧ୍ୟରେ ତାପମାତ୍ରା ଅନୁଭୂତ ହେଉଥିବା ଅଞ୍ଚଳରେ ଚାହା ଚାଷ କରାଯାଏ ।
- ବାର୍ଷିକ ହାରହାରି ବୃଷ୍ଟିପାତର ପରିମାଣ 150 ସେ.ମି.ରୁ 200 ସେ.ମି. ଏହି ଚାଷ ପାଇଁ ଉପଯୁକ୍ତ ।
- ଏହି ଚାଷ ନିମନ୍ତେ ପ୍ରଚୁର ବୃଷ୍ଟିପାତ ଆବଶ୍ୟକ ହେଉଥିଲେ ମଧ୍ୟ ଚାହା ଗଛ ମୂଳରେ ପାଣି ଜମିରହିଲେ ତାହା ମରିଯାଏ ।
ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ସଂକ୍ଷେପରେ ଉତ୍ତର ଲେଖ ।
Question 1.
ପ୍ରାଥମିକ ପ୍ରକ୍ରିୟା କ’ଣ ଉଦାହରଣ ସହ ବୁଝାଅ ।
Answer:
ପ୍ରାକୃତିକ ପରିବେଶରୁ ବିଭିନ୍ନ ଦ୍ରବ୍ୟ ସଂଗ୍ରହ; ଯଥା— ଜମିରୁ ଶସ୍ୟ ଉତ୍ପାଦନ, ନଦୀ, ଜଳାଶୟ ଓ ସମୁଦ୍ରରୁ ମତ୍ସ୍ୟ ସଂଗ୍ରହ, ଜଙ୍ଗଲରୁ କାଠ, ବାଉଁଶ, ଫଳ, ଝୁଣା, ମହୁ ଆଦି ଦ୍ରବ୍ୟ ସଂଗ୍ରହ, ଖଣିରୁ ଧାତୁ ଉତ୍ତୋଳନ, ପଶୁପାଳନ ଇତ୍ୟାଦି କାର୍ଯ୍ୟଗୁଡ଼ିକ ପ୍ରାଥମିକ ପ୍ରକ୍ରିୟାର ଅନ୍ତର୍ଭୁକ୍ତ ।
![]()
Question 2.
ଦ୍ଵିତୀୟକ ପ୍ରକ୍ରିୟା କ’ଣ ବୁଝାଇ ଲେଖ ।
Answer:
ବିଭିନ୍ନ ଦ୍ରବ୍ୟକୁ ଯାନ୍ତ୍ରିକ ପଦ୍ଧତିରେ ପରିବର୍ତ୍ତନ କରି ବ୍ୟବହାର ଉପଯୋଗୀ ସାମଗ୍ରୀରେ ପ୍ରସ୍ତୁତ କରିବା; ଯଥା – ଧାନରୁ
ଚାଉଳ, ଗହମରୁ ଅଟା, କପାରୁ ଲୁଗା, ଆଖୁରୁ ଚିନି, ବାଉଁଶରୁ କାଗଜ, ତୈଳବୀଜରୁ ତେଲ, ଖଣିଜଦ୍ରବ୍ୟରୁ ବିଭିନ୍ନ ଯନ୍ତ୍ରପାତି ତିଆରି ଇତ୍ୟାଦି ଦ୍ଵିତୀୟକ କାର୍ଯ୍ୟକଳାପର ଅନ୍ତର୍ଭୁକ୍ତ ।
Question 3.
କପାଚାଷ ପାଇଁ ଆବଶ୍ୟକୀୟ ମୃରିକା ଓ ଜଳବାୟୁ ବିଷୟରେ ଲେଖ ।
Answer:
- ପଟୁ, ପଙ୍କ, ଜୈବସାର ଥିବା ଭଲ ହୁଏ । କୃଷ୍ଣକାର୍ପାସ ମୃର୍ତ୍ତିକା କପାଚାଷ ନିମନ୍ତେ ସର୍ବୋତ୍କୃଷ୍ଟ ।
- ଅଧିକ ବୃଷ୍ଟିପାତ, ଅଧିକ ତାପମାତ୍ରା ଓ ଉତ୍ତମ ଜଳସେଚନ ଏହି ଚାଷ ପାଇଁ ଆବଶ୍ୟକ ହୋଇଥାଏ । କପାଗଛ ବଢ଼ିବା ଓ କପା ଫୁଟିବା ପାଇଁ ଉଜ୍ଜ୍ଵଳ ସୂର୍ଯ୍ୟକିରଣ ଓ ଖରାପାଗ ଦରକାର ହୋଇଥାଏ ।
Question 4.
ରୋପଣ କୃଷି କାହାକୁ କହନ୍ତି ? ଉଦାହରଣସହ ବୁଝାଅ ।
Answer:
- ଫସଲ ରୋପଣଦ୍ୱାରା କରାଯାଉଥିବା କୃଷିକାର୍ଯ୍ୟକୁ ରୋପଣ କୃଷି କୁହାଯାଏ ।
- କ୍ରାନ୍ତି ମଣ୍ଡଳର ବିସ୍ତୃତ ଅଞ୍ଚଳର ଏକକ ଫସଲ ଭାବରେ ଏହି କୃଷି କରାଯାଇଥାଏ । ଚାହା, କଫି, ଆଖୁ ଓ ରବର ଏହି କୃଷିରୁ ଉଦାହରଣ ।
Question 5.
ଗହମ ଉତ୍ପାଦନରେ ପୃଥିବୀରେ ଏବଂ ଭାରତରେ ଅଗ୍ରଣୀ ଦେଶ ତଥା ରାଜ୍ୟଗୁଡ଼ିକର ନାମ ଉଲ୍ଲେଖ କର ।
Answer:
- ପୃଥିବୀରେ ଗହମ ଉତ୍ପାଦନରେ ଅଗ୍ରଣୀ ଦେଶଗୁଡ଼ିକ ହେଲେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ଓ ରୁଷିଆ ।
- ଭାରତରେ ପଞ୍ଜାବ, ହରିୟାଣା, ରାଜସ୍ଥାନ ଓ ଉତ୍ତରପ୍ରଦେଶ ଗହମ ଉତ୍ପାଦନରେ ‘ଅଗ୍ରଣୀ ରାଜ୍ୟ ଅଟନ୍ତି ।
![]()
Question 6.
ଧାନ ଚାଷରେ ପୃଥିବୀ ଏବଂ ଭାରତର ଅଗ୍ରଣୀ ଦେଶ ଏବଂ ରାଜ୍ୟମାନଙ୍କର ନାମ ଲେଖ ।
Answer:
ଧାନଚାଷରେ ପୃଥିବୀରେ ପ୍ରସିଦ୍ଧିଲାଭ କରିଥିବା ଦେଶଗୁଡ଼ିକ ହେଲେ ଚୀନ୍, ଭାରତ, ଜାପାନ ଓ ଶ୍ରୀଲଙ୍କା । ଭାରତରେ ପଶ୍ଚିମବଙ୍ଗ, ଆନ୍ଧ୍ରପ୍ରଦେଶ, ଉତ୍ତରପ୍ରଦେଶ, ଓଡ଼ିଶା, ତାମିଲନାଡୁ ଓ ଉତ୍ତରାଖଣ୍ଡ ଆଦି ରାଜ୍ୟ ଧାନଚାଷ ପାଇଁ ପ୍ରସିଦ୍ଧ ।
Question 7.
ଚାହା ଉତ୍ପାଦନରେ ପୃଥିବୀ ଏବଂ ଭାରତର ଚାରିଗୋଟି ଅଗ୍ରଣୀ ଅଞ୍ଚଳର ନାମ ଲେଖ ।
Answer:
ପୃଥିବୀରେ ଚୀନ୍, ଭାରତ, ଶ୍ରୀଲଙ୍କା ଓ କେନିଆ ଚାହା ଉତ୍ପାଦନରେ ମୁଖ୍ୟ ସ୍ଥାନ ଅଧିକାର କରିଥିବାବେଳେ ଭାରତର ଆସାମ, ପଶ୍ଚିମବଙ୍ଗ, କେରଳ ଓ କର୍ଣ୍ଣାଟକ ରାଜ୍ୟଗୁଡ଼ିକ ପ୍ରସିଦ୍ଧିଲାଭ କରିଛନ୍ତି ।
Question 8.
ପୃଥିବୀ ଏବଂ ଭାରତର ମୁଖ୍ୟ ମକା ଉତ୍ପାଦନକାରୀ ଅଞ୍ଚଳର ନାମ ଲେଖ ।
Answer:
- ପୃଥିବୀର ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ଚୀନ୍, ବ୍ରାଜିଲ, ଆର୍ଜେଣ୍ଟିନା, ମେକ୍ସିକୋ, ରୁଷିଆ, କାନାଡ଼ା ଆଦି ଦେଶରେ ମକା ପ୍ରଚୁର ପରିମାଣରେ ଚାଷ କରାଯାଏ ।
- ଭାରତର ଉତ୍ତରପ୍ରଦେଶ, ବିହାର, ପଞ୍ଜାବ, ଜାମ୍ମୁ ଓ କାଶ୍ମୀର ଏବଂ ରାଜସ୍ଥାନ, ହରିୟାଣା, ମଧ୍ୟପ୍ରଦେଶ ଆଦି ରାଜ୍ୟମାନଙ୍କରେ ମକା ଅଧିକ ପରିମାଣରେ ଚାଷ କରାଯାଏ ।
Question 9.
ବାଜରା ଉତ୍ପାଦନରେ ପୃଥିବୀର ଅଗ୍ରଣୀ ଦେଶଗୁଡ଼ିକର ନାମ ଉଲ୍ଲେଖ କର ।
Answer:
ବାଜରା ଉତ୍ପାଦନରେ ପୃଥିବୀରେ ଭାରତ, ଚୀନ୍, ନାଇଜେରିଆ ଓ ନାଇଜର ଆଦି ଦେଶଗୁଡ଼ିକ ପ୍ରଧାନ ।
Question 10.
ବାଜରା ଉତ୍ପାଦନରେ ଭାରତ ଏବଂ ଓଡ଼ିଶାର ମୁଖ୍ୟ ଅଞ୍ଚଳଗୁଡ଼ିକର ନାମ ଉଲ୍ଲେଖ କର ।
Answer:
ବାଜରା ଉତ୍ପାଦନରେ ରାଜସ୍ଥାନ, କର୍ଣ୍ଣାଟକ, ମହାରାଷ୍ଟ୍ର, ମଧ୍ୟପ୍ରଦେଶ, ଉତ୍ତର ପ୍ରଦେଶ, ଗୁଜରାଟ ଓ ହରିୟାଣା ପ୍ରଧାନ ଅଞ୍ଚଳ ହୋଇଥିବାବେଳେ ଓଡ଼ିଶା ରାଜ୍ୟର ଗଜପତି ଓ ଗଞ୍ଜାମ ଜିଲ୍ଲାରେ ଅଧିକ ପରିମାଣରେ ଉତ୍ପାଦନ କରାଯାଏ ।
![]()
Question 11.
କପାଚାଷ ପାଇଁ ଭାରତର ଅଗ୍ରଣୀ ରାଜ୍ୟଗୁଡ଼ିକର ନାମ ଲେଖ ।
Answer:
ଭାରତରେ ମହାରାଷ୍ଟ୍ର, ମଧ୍ୟପ୍ରଦେଶ, ଗୁଜରାଟ, ଆନ୍ଧ୍ରପ୍ରଦେଶ, କର୍ଣ୍ଣାଟକ ଓ ହରିୟାଣା ଅଞ୍ଚଳ କପାଚାଷରେ ଅଗ୍ରଣୀ ରାଜ୍ୟ ।
Question 12.
ଭାରତର କେଉଁ କେଉଁ ରାଜ୍ୟରେ ଝୋଟଚାଷ କରାଯାଏ ?
Answer:
ଭାରତର ପଶ୍ଚିମବଙ୍ଗ, ଆସାମ, ଓଡ଼ିଶା ଓ ଉତ୍ତରପ୍ରଦେଶ ଆଦି ରାଜ୍ୟମାନଙ୍କରେ ଝୋଟଚାଷ କରାଯାଏ ।
Question 13.
ପୃଥିବୀ ଏବଂ ଭାରତରେ କଫିଚାଷ ହେଉଥିବା ଅଗ୍ରଣୀ ଅଞ୍ଚଳଗୁଡ଼ିକର ନାମ ଉଲ୍ଲେଖ କର ।
Answer:
- ପୃଥିବୀରେ କଫି ଉତ୍ପାଦନରେ ଅଗ୍ରଣୀ ରାଷ୍ଟ୍ରଗୁଡ଼ିକ ହେଲେ ବ୍ରାଜିଲ, ପେରୁ, କେନିଆ, ଆଇଭରି କୋଷ୍ଟ, ମାଲାଗାସୀ, କଲମ୍ବିଆ, ଫିଲିପାଇନ୍ସ ।
- ଭାରତର ରାଜ୍ୟମାନଙ୍କ ମଧ୍ୟରେ କର୍ଣ୍ଣାଟକ, ତାମିଲନାଡୁ ଓ କେରଳ କଫି ଉତ୍ପାଦନରେ ଅଗ୍ରଣୀ ରାଜ୍ୟ ଅଟନ୍ତି ।
ଭୌଗୋଳିକ କାରଣ ଦର୍ଶାଅ ।
Question 1.
ବ୍ରାଜିଲରେ ପ୍ରଚୁର କଫିଚାଷ କରାଯାଏ ।
Answer:
- କଫି ଚାଷ ଲାଭା ମୃରିକା, ଲାଟେରାଇଟ୍ ମୃରିକା, ଦୋରସା ଓ ବାଲିଆ ମାଟିରେ ଭଲ ହୁଏ । ଏହା ମଧ୍ଯ କ୍ରାନ୍ତୀମଣ୍ଡଳୀୟ ଏକ ରୋପଣ କୃଷି ।
- ସମୁଦ୍ର ପତ୍ତନଠାରୁ 350 ମିଟରଠାରୁ 1830 ମିଟର ଉଚ୍ଚତା ବିଶିଷ୍ଟ ସ୍ଥାନମାନଙ୍କରେ କଫିଚାଷ ଭଲ ହୁଏ । ବ୍ରାଜିଲ୍ର ସାଓପାଓଲୋର ମାଳଅଞ୍ଚଳ ଗଡ଼ାଣିଆ ଭୂମି ଏହି ଚାଷପାଇଁ ଉପଯୋଗୀ ହୋଇଥିବାରୁ ଏଠାରେ ପ୍ରଚୁର କଫି ଚାଷ କରାଯାଏ ।
Question 2.
ଚାହା ଭାରତର ଏକ ପ୍ରଧାନ ପଣ୍ୟଦ୍ରବ୍ୟ ।
Answer:
- ଭାରତର ଆସାମ, ପଶ୍ଚିମବଙ୍ଗର ଦାର୍ଜିଲିଂ ପାର୍ବତ୍ୟ ଅଞ୍ଚଳ, ଦକ୍ଷିଣ ଭାରତର ନୀଳଗିରି ଓ କେରଳରେ ଅଧିକ ଚାହାଚାଷ ହୁଏ ।
- ଭାରତୀୟ ଚାହାର ବିଦେଶରେ ବିଶେଷ ଚାହିଦା ଥିବାରୁ ଗ୍ରେଟ୍ ବ୍ରିଟେନ୍, ଫ୍ରାନ୍ସ, ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, କାନାଡ଼ା, ଅଷ୍ଟ୍ରେଲିଆ ପ୍ରଭୃତି ଦେଶମାନଙ୍କୁ ରପ୍ତାନି ହୁଏ । ତେଣୁ ଚାହା ଭାରତର ଏକ ପ୍ରଧାନ ପଣ୍ୟଦ୍ରବ୍ୟ ।
![]()
Question 3.
ଚୀନ ଧାନ ଉତ୍ପାଦନରେ ପ୍ରଧାନ ସ୍ଥାନ ଅଧିକାର କରିଛି ।
Answer:
- ଧାନ ଏକ କ୍ରାନ୍ତିମଣ୍ଡଳୀୟ ଫସଲ । ଚୀନ ଦେଶ ଜନବହୁଳ ହୋଇଥିବାରୁ କୃଷିକାର୍ଯ୍ୟ ନିମନ୍ତେ ଅଧୁକ ଶ୍ରମିକ ମିଳିଥା’ନ୍ତି । ଧାନଚାଷ ପାଇଁ ଆବଶ୍ୟକ ବୃଷ୍ଟିପାତ ଓ ତାପମାତ୍ରା ଏଠାରେ ଉପଲବ୍ଧ ହୋଇଥାଏ ।
- ଚୀନର ଅଧିକାଂଶ ଅଞ୍ଚଳର ମୃରିକା ଦୋରସା, ପଟୁ ଓ ମଟାଳ ହୋଇଥିବାରୁ ଏଠାରେ ପ୍ରଚୁର ଧାନଚାଷ କରାଯାଏ ।
Question 4.
ପଶ୍ଚିମ ଭାରତରେ ଶୁଷ୍କ କୃଷି କାର୍ଯ୍ୟ କରାଯାଏ ।
Answer:
- ପଶ୍ଚିମ ଭାରତରେ ସ୍ଵଳ୍ପ ବୃଷ୍ଟିପାତ ହୋଇଥାଏ । ସ୍ୱଳ୍ପ ବୃଷ୍ଟିପାତ ହେତୁ ଜମିକୁ ଗଭୀର ଋଷ କରାଯାଏ । ଜମିରେ ଅଧିକ ସମୟ ଜଳ ରହିବା ପାଇଁ ଜମିକୁ ଛୋଟ ଛୋଟ କିଆରିରେ ଭାଗ କରାଯାଇଛି ।
- ଯଅ, ବାଜରା, ମାଣ୍ଡିଆ ଆଦି ଏ ଅଞ୍ଚଳର ପ୍ରଧାନ ଫସଲ।
Question 5.
ରୋପଣ କୃଷିକୁ ବାଣିଜ୍ୟଭିଭିକ କୃଷି କୁହାଯାଏ ।
Answer:
- ଋହା, କଫି, ରବର, ଆଖୁ, ନଡ଼ିଆ, ସପୁରୀ, କଦଳୀ, କାଜୁ ଇତ୍ୟାଦି ଜମିରେ ଏକ ଋଷ ଭାବରେ ରୋପଣ କରାଯାଇଥାଏ।
- ଏଗୁଡ଼ିକ ଅର୍ଥକରୀ ଫସଲ ହୋଇଥିବାରୁ ଏହାକୁ ବାଣିଜ୍ୟଭିଭିକ କୃଷି କୁହାଯାଏ।
Question 6.
ବାଙ୍ଗଲାଦେଶରେ ଝୋଟ ଋଷ ଅଧ୍ବକ କରାଯାଏ।
Answer:
- ଝୋଟ ଋଷ ପାଇଁ ପଟୁ ମୃରିକା, ଆର୍ଦ୍ର ଜଳବାୟୁ ଓ ଅତ୍ୟଧିକ ବୃଷ୍ଟିପାତ ଆବଶ୍ୟକ ।
- ବାଙ୍ଗଲାଦେଶର ନଦୀ ଜଳ ପ୍ଲାବିତ ପଟୁମାଟିରେ ବ୍ୟାପକ ଭାବରେ ଝୋଟ ଋଷ କରି ଝୋଟଜାତ ଦ୍ରବ୍ୟ ବିଦେଶକୁ ରପ୍ତାନି କରେ ।
ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।
1. ଝୁମ୍ ଚାଷ ଓ ପୁନମ୍ ଚାଷ
Answer:

![]()
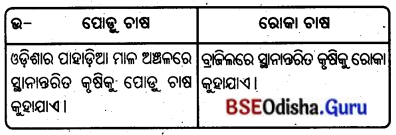
2. ପୋଡ଼ୁ ଚାଷ ଓ ରୋକା ଚାଷ :
Answer:
3. ମିଶ୍ରିତ କୃଷି ଓ ଏକକ କୃଷି :
Answer:

4. ରାଞ୍ଚ୍ ଓ ସ୍ଵଷ୍ଠିତନ୍ତୁ :
Answer:
![]()
5. ଖରିଫ୍ ଫସଲ ଓ ରବି ଫସ୍ଲ :
Answer:
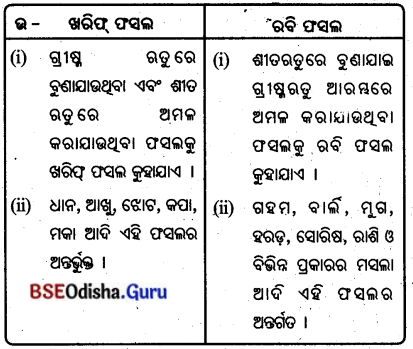
6. ମିଶ୍ରିତ କୃଷି ଓ ଉଦ୍ୟାନ କୃଷି :
Answer:
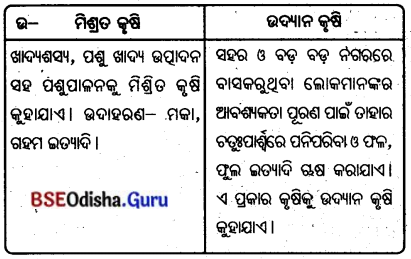
ପରୀକ୍ଷା ଉପଯୋଗୀ ସମ୍ଭାବିତ ପ୍ରଶ୍ନୋତ୍ତର
ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶ୍ନୋତ୍ତର
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
1. ପୃଥିବୀର ବୃହତ୍ତମ କଫି ଋଷ ଅଞ୍ଚଳର ନାମ …………….
Answer: ସାଓପାଓଲୋ
2. ……………. ଦେଶରେ ପ୍ରଥମେ ଚାହାର ବ୍ୟବହାର କରାଯାଇଥିଲା ।
Answer: ଚୀନ୍
3. ……………. ଦେଶରେ ଏକର ପିଛା ସବୁଠାରୁ ବେଶୀ କପା ଋଷ କରାଯାଏ।
Answer: ଇଜିପ୍ଟ
![]()
4. ଭାରତର ଧାନ ଏକ ………….. ଫସଲ ଅଟେ ।
Answer: ଖରିଫ
5. ଆମ ଦେଶରେ ଧାନ ଋଷ …………. ଭିଭିକ ବୃତ୍ତି ଅଟେ।
Answer: ଶ୍ରମ
6. ପୃଥିବୀର ସର୍ବାଧିକ ଲୋକଙ୍କର ପ୍ରଧାନ ଖାଦ୍ୟଶସ୍ୟ, ………….. ଉତ୍ତର
Answer: ଧାନ
ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।
Question 1.
କେଉଁ କାର୍ଯ୍ୟଗୁଡ଼ିକ ତୃତୀୟକ ପ୍ରକ୍ରିୟାର ଅନ୍ତର୍ଗତ ?
Answer:
ପରିବହନ, ବ୍ୟାଙ୍କ, ବୀମା, ବାଣିଜ୍ୟ, ଟେଲିଫୋନ, ବିଦ୍ୟୁତ୍ ଶକ୍ତି ଯୋଗାଣ ଇତ୍ୟାଦି ସେବା କାର୍ଯ୍ୟଗୁଡ଼ିକ ତୃତୀୟକ ପ୍ରକ୍ରିୟାର ଅନ୍ତର୍ଗତ।
Question 2.
ନିବେଶ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଦ୍ରବ୍ୟ ଉତ୍ପାଦନରେ ବ୍ୟବହାର କରାଯାଉଥିବା ଆବଶ୍ୟକୀୟ ଉପାଦାନକୁ ନିବେଶ କୁହାଯାଏ।
Question 3.
କୃଷିକାର୍ଯ୍ୟ ପାଇଁ କେଉଁସବୁ ଉପଯୁକ୍ତ ପରିବେଶ ଆବଶ୍ୟକ ହୋଇଥାଏ ?
Answer:
ସୌରତାପ, ବୃଷ୍ଟିପାତ, ଭୂମିର ଗଠନ, ଉପଯୋଗୀ ମ୍ପରିକା ଇତ୍ୟାଦି କୃଷିକାର୍ଯ୍ୟ ପାଇଁ ଆବଶ୍ୟକ ।
![]()
Question 4.
କେଉଁ କାର୍ଯ୍ୟଗୁଡ଼ିକ ପ୍ରାକୃତିକ ନିବେଶ ଅଟେ ?
Answer:
ସୂର୍ଯ୍ୟାଲୋକ, ଉତ୍ତାପ, ବୃଷ୍ଟିପାତ, ଭୂମିର ଗଠନ ଓ ମୃତ୍ତିକା ପ୍ରାକୃତିକ ନିବେଶ ଅଟେ।
Question 5.
କେଉଁ ଦେଶମାନଙ୍କରେ ପ୍ରୟୋଜନଭିଭିକ କୃଷିକାର୍ଯ୍ୟ ବିଶେଷ ଭାବରେ ପ୍ରଚଳିତ ?
Answer:
ଭାରତ ଓ ଚୀନରେ ପ୍ରୟୋଜନଭିଭିକ କୃଷିକାର୍ଯ୍ୟ ବିଶେଷ ଭାବରେ ପ୍ରଚଳିତ।
Question 6.
ପ୍ରୟୋଜନଭିତ୍ତିକ କୃଷିରେ ଉତ୍ପାଦନ କମ୍ ହେବାର କାରଣ କ’ଣ ?
Answer:
ଏକ ପ୍ରକାର କୃଷି କାର୍ଯ୍ୟ କରୁଥିବା ଚାଷୀ ଗରିବ ହେତୁ ଜମିରେ ରାସାୟନିକ ସାର, କୀଟନାଶକ ଦ୍ରବ୍ୟର ପ୍ରୟୋଗ ଓ ଅଧିକ ଅମଳକ୍ଷମ ବିହନ ବ୍ୟବହାର କରିପାରେ ନାହିଁ। ଜଳସେଚନର ଅଭାବ ହେତୁ ଜମିର ଉତ୍ପାଦନ କମ୍ ହୁଏ।
Question 7.
ସ୍ଥାନାନ୍ତରିତ କୃଷିକୁ କର୍ଜନ ଓ ଦହନ କୃଷି କୁହାଯାଏ କାହିଁକି ?
Answer:
ଜଙ୍ଗଲ କାଟି ଓ ପୋଡ଼ି ଜମିରେ ଚାଷ କରାଯାଉଥିବାରୁ ଏହାକୁ ‘ କର୍ତ୍ତନ ଓ ଦହନ’ କୃଷି ବୋଲି କୁହାଯାଏ।’
Question 8.
ଝୁମ୍ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଉତ୍ତର-ପୂର୍ବ ଭାରତରେ ସ୍ଥାନାନ୍ତରିତ କୃଷିକୁ ଝୁମ୍ କୁହାଯାଏ।
Question 9.
‘ ରୋକୋ’ କେଉଁ ଦେଶର ସ୍ଥାନାନ୍ତରିତ କୃଷି ?
Answer:
‘ରୋକୋ’ ବ୍ରାଜିଲ୍ର ସ୍ଥାନାନ୍ତରିତ କୃଷି ।
![]()
Question 10.
ସଘନ ପ୍ରୟୋଜନଭିଭିକ କୃଷି କାହାକୁ କୁହାଯାଏ ?
Answer:
ଛୋଟ ଛୋଟ ଜମିରେ ଉନ୍ନତ ବିହନ, ନିୟମିତ ଜଳସେଚନ, ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାଣରେ ସାର ପ୍ରୟୋଗ କରି ଅଧ୍ବକ ଶ୍ରମିକଦ୍ଵାରା ଚାଷ କରି ଅଧୂକ ଫସଲ ଉତ୍ପାଦନକୁ ସଘନ ପ୍ରୟୋଜନ ଭିତ୍ତିକ କୃଷି କୁହାଯାଏ|
Question 11.
କେଉଁ କୃଷିଗୁଡ଼ିକ ସଘନ ପ୍ରୟୋଜନଭିଭିକ କୃଷିର ଅନ୍ତର୍ଗତ ?
Answer:
ଗହମ, ମକା, ଡାଲିଜାତୀୟ ଶସ୍ୟ, ତୈଳବୀଜ ଇତ୍ୟାଦି ସଘନ ପ୍ରୟୋଜନଭିଭିକ କୃଷିର ଅନ୍ତର୍ଗତ।
Question 12.
ଅର୍ଥକରୀ କୃଷି କାହାକୁ କୁହାଯାଏ ?
Answer:
ଯେଉଁ କୃଷି ଦେଶର ଆବଶ୍ୟକତା ପୂରଣ ପରେ ବିଦେଶକୁ ରପ୍ତାନି କରାଯାଇ ସେଥୁରୁ ଅର୍ଥୋପାର୍ଜନ କରାଯାଏ, ତାକୁ ଅର୍ଥକରୀ ଫସଲ କୁହାଯାଏ ।
Question 13.
ଭାରତର କେଉଁ ରାଜ୍ୟରେ ଗହମ ଚାଷ କରାଯାଇ ରପ୍ତାନି କରାଯାଏ ?
Answer:
ଭାରତର ପଞ୍ଜାବ ଓ ହରିୟାଣା ରାଜ୍ୟରେ ଗହମ ଚାଷ କରାଯାଇ ରପ୍ତାନି କରାଯାଏ।
Question 14.
ମିଶ୍ରିତ କୃଷି କାହାକୁ କୁହାଯାଏ ?
Answer:
ଖାଦ୍ୟଶସ୍ୟ, ପଶୁଖାଦ୍ୟ ଉତ୍ପାଦନ ସହ ପଶୁପାଳନକୁ ମିଶ୍ରିତ କୃଷି କୁହାଯାଏ ।
Question 15.
ମିଶ୍ରିତ କୃଷି କେଉଁ ଜଳବାୟୁ ଅଞ୍ଚଳରେ ହୋଇଥାଏ ?
Answer:
ମିଶ୍ରିତ କୃଷି କ୍ରାନ୍ତୀୟ ଜଳବାୟୁ ଅଞ୍ଚଳରେ ହୋଇଥାଏ।
![]()
Question 16.
ରାଞ୍ଚ୍ କ’ଣ ?
Answer:
ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ପଶୁଚାରଣ ଭୂମିକୁ ରାଞ୍ଚ୍ କୁହାଯାଏ।
Question 17.
କେଉଁ କୃଷିଗୁଡ଼ିକ ଉଦ୍ୟାନ କୃଷିର ଅନ୍ତର୍ଗତ ?
Answer:
କଦଳୀ, ଆମ୍ବ, ପଣସ, ନଡ଼ିଆ ଓ ଫୁଲଚାଷ ଉଦ୍ୟାନ କୃଷିର ଅନ୍ତର୍ଗତ ।
Question 18.
ଓଡ଼ିଶାରୁ କେଉଁ କୃଷିଜାତ ଦ୍ରବ୍ୟ ବିଦେଶକୁ ରପ୍ତାନି ହୁଏ ?
Answer:
ଓଡ଼ିଶାରୁ ପାନ ବିଦେଶକୁ ରପ୍ତାନି ହୁଏ।
Question 19.
ଭାରତର କେଉଁ ରାଜ୍ୟରୁ ନଡ଼ିଆ ବିଦେଶକୁ ରପ୍ତାନି ହୁଏ ?
Answer:
ଭାରତର କେରଳରୁ ନଡ଼ିଆ ବିଦେଶକୁ ରପ୍ତାନି ହୁଏ।
Question 20.
କେଉଁ ଦେଶ ଚାହା ଉତ୍ପାଦନରେ ଅଗ୍ରଣୀ ?
Answer:
ଭାରତ ଓ ଶ୍ରୀଲଙ୍କା ଚାହା ଉତ୍ପାଦନରେ ଅଗ୍ରଣୀ।
Question 21.
ବ୍ରାଜିଲ କେଉଁ ରୋପଣ କୃଷି ପାଇଁ ଅଗ୍ରଣୀ ?
Answer:
କଫି ରୋପଣ କୃଷି ପାଇଁ ବ୍ରାଜିଲ୍ ଅଗ୍ରଣୀ।
![]()
Question 22.
ଆଖୁ ଚାଷରେ କେଉଁ ଦେଶ ଅଗ୍ରଣୀ ?
Answer:
କ୍ୟୁବା ଆଖୁଚାଷରେ ଅଗ୍ରଣୀ।
Question 23.
ଶୁଷ୍କ କୃଷି ଅଞ୍ଚଳରେ କେଉଁ ଫସଲମାନ କରାଯାଏ ?
Answer:
ଶୁଷ୍କ କୃଷି ଅଞ୍ଚଳରେ ଯଅ, ବାଜରା, ମାଣ୍ଡିଆ ଓ କମ୍ ଜଳ ଆବଶ୍ୟକ କରୁଥିବା ଫସଲ କରାଯାଏ।
Question 24.
କେଉଁ ଅଞ୍ଚଳରେ ଶୁଷ୍କ କୃଷି କାର୍ଯ୍ୟ କରାଯାଇଥାଏ ?
Answer:
ମଧ୍ୟ ପ୍ରାଚ୍ୟ ଓ ପଶ୍ଚିମ ଭାରତରେ ଶୁଷ୍କ କୃଷି କାର୍ଯ୍ୟ କରାଯାଇଥାଏ।
Question 25.
ଆର୍ଦ୍ର କୃଷି କାହାକୁ କୁହାଯାଏ ?
Answer:
ଅଧିକ ବୃଷ୍ଟିପାତ ଅଞ୍ଚଳରେ କରାଯାଉଥିବା କୃଷିକୁ ଆର୍ଦ୍ର କୃଷି କୁହାଯାଏ; ଯଥା ଧାନ ଓ ନଳିତା ।
Question 26.
ଗହମ କେଉଁ ଅଞ୍ଚଳରେ ଚାଷ କରାଯାଏ ?
Answer:
ନାତିଶୀତୋଷ୍ଣ ମଣ୍ଡଳରେ ଥିବା ପୃଥିବୀର ବିଭିନ୍ନ ଅଞ୍ଚଳରେ ଗହମ ଚାଷ କରାଯାଏ।
Question 27.
ଧାନ ଚାଷ ପାଇଁ କି ପ୍ରକାର ଜଳବାୟୁ ଆବଶ୍ୟକ ?
Answer:
ଧାନ ଫସଲ ଅଧିକ ଉତ୍ତାପ, ଅଧିକ ଆର୍ଦ୍ରତା ଓ ଅଧିକ ବୃଷ୍ଟି ଦରକାର କରେ।
![]()
Question 28.
କେଉଁ ପ୍ରକାର ମାଟିରେ ଧାନ ଚାଷ ଭଲ ହୁଏ ?
Answer:
ମଟାଳ, ପଟୁ ଓ ଦୋରସା ମାଟିରେ ଧାନ ଚାଷ ଭଲ ହୁଏ।
Question 29.
ମକା ଉତ୍ପାଦନରେ କେଉଁ ଦେଶ ପୃଥିବୀରେ ପ୍ରଥମ ସ୍ଥାନ ଅଧିକାର କରିଛି ?
Answer:
ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ମକା ଉତ୍ପାଦନରେ ପୃଥିବୀରେ ପ୍ରଥମ ସ୍ଥାନ ଅଧିକାର କରିଛି ।
Question 30.
ଭାରତର କେଉଁ ରାଜ୍ୟ ବାଜରା ଉତ୍ପାଦନରେ ଅଗ୍ରଣୀ ?
Answer:
ଭାରତର ରାଜସ୍ଥାନ ବାଜରା ଉତ୍ପାଦନରେ ଅଗ୍ରଣୀ
Question 31.
କେଉଁ ମୃଭିକାରେ କପାଚାଷ ଅଧିକ କରାଯାଏ ?
Answer:
କୃଷ୍ଣ ମୃତ୍ତିକାରେ କପାଚାଷ ଅଧିକ କରାଯାଏ।
Question 32.
କେଉଁ ଦେଶରେ ଦୀର୍ଘ ତନ୍ତୁଯୁକ୍ତ କପା ଉତ୍ପାଦନ କରାଯାଏ ?
Answer:
ଇଜିପ୍ଟରେ ଦୀର୍ଘ ତନ୍ତୁଯୁକ୍ତ କପା ଉତ୍ପାଦନ କରାଯାଏ।
Question 33.
କାହାକୁ ସ୍ଵଷ୍ଠିତରୁ କୁହାଯାଏ ?
Answer:
ଝୋଟକୁ ସ୍ଵତନ୍ତୁ କୁହାଯାଏ।
![]()
Question 34.
କେଉଁ ଦେଶମାନଙ୍କରେ ଝୋଟଚାଷ ଅଧ୍ଵକ କରାଯାଏ ?
Answer:
ବାଙ୍ଗଲାଦେଶ ଓ ଭାରତରେ ଝୋଟି ଚାଷ ଅଧ୍ଵକ କରାଯାଏ।
Question 35.
ଭାରତର କେଉଁ ଅଞ୍ଚଳରେ ଚାହା ବଗିଚା ଅଧ୍ବକ ଦେଖାଯାଏ ?
Answer:
ଆସାମ ଓ ପଶ୍ଚିମବଙ୍ଗର ଦାର୍ଜିଲିଂ ପାର୍ବତ୍ୟାଞ୍ଚଳରେ ଚାହା ବଗିଚା ଅଧିକ ଦେଖାଯାଏ ।
Question 36.
ପୃଥିବୀର କେଉଁ ଅଞ୍ଚଳ ବୃହତ୍ କଫି ଚାଷ ଅଞ୍ଚଳ ଅଟେ ?
Answer:
ବ୍ରାଜିଲ୍ ଦେଶର ସାଓପାଓଲୋ ମାଳ ଅଞ୍ଚଳ ବୃହତ୍ କଫି ଚାଷ ଅଞ୍ଚଳ ଅଟେ।
Question 37.
ଭାରତରେ ଶତକଡ଼ା କେତେ ଭାଗ କଫି ଉତ୍ପାଦନ କରାଯାଏ ?
Answer:
ଭାରତରେ ଶତକଡ଼ା ୪ ଭାଗ କଫି ଉତ୍ପାଦନ କରାଯାଏ।
Question 38.
କେଉଁ ମହାଦେଶରେ ଭାରତର କଫିର ଚାହିଦା ଅଧ୍ବକ ?
Answer:
ଇଉରୋପ ଓ ଅଷ୍ଟ୍ରେଲିଆ ମହାଦେଶରେ ଭାରତର କଫିର ଚାହିଦା ଅଧିକ ।
Question 39.
ଭାରତର କେଉଁ ରାଜ୍ୟରେ କଫି ଚାଷ କରାଯାଏ ?
Answer:
କର୍ଣ୍ଣାଟକ, ତାମିଲନାଡୁ ଓ କେରଳରେ କଫି ଚାଷ କରାଯାଏ।
Question 40.
ଓଡ଼ିଶାର କେଉଁଠାରେ କଫିଚାଷ କରାଯାଉଛି ?
Answer:
ଓଡ଼ିଶାର କୋରାପୁଟ ଓ ନବରଙ୍ଗପୁରଠାରେ କଫିଚାଷ କରାଯାଉଛି ।
ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଦିଅ ।
Question 1.
ସ୍ଥାନାନ୍ତରିତ କୃଷିର ଅନ୍ୟନାମ କ’ଣ ?
Answer:
କର୍ଜନ ଓ ଦହନ କୃଷି
![]()
Question 2.
କେରଳରେ ପୁନମ୍ କେଉଁମାନେ କରିଥାନ୍ତି ?
Answer:
ଆଦିବାସୀ
Question 3.
ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ପଶୁଗରଣ ଭୂମିକୁ କ’ଣ କୁହାଯାଏ ?
Answer:
ରାଞ୍ଚ୍
Question 4.
ଓଡ଼ିଶାର ପାନ ଚାଷ କେଉଁ କୃଷିର ଅନ୍ତର୍ଭୁକ୍ତ ?
Answer:
ଉଦ୍ୟାନ କୃଷି
Question 5.
ଜଳସେଚନଦ୍ଵାରା କରାଯାଉଥିବା କୃଷିକାର୍ଯ୍ୟକୁ କ’ଣ କୁହାଯାଏ ?
Answer:
ସେଚିତ କୃଷି
Question 6.
କେଉଁ କୃଷି ପାଇଁ ଅଧିକ ପୁଞ୍ଜି, ବିସ୍ତୃତ ଭୂମି ଓ ଅଧିକ ଶ୍ରମିକ ଆବଶ୍ୟକ ?
Answer:
ରୋପଣ
![]()
Question 7.
ଶୁଷ୍କ କୃଷି ଭାରତର କେଉଁ ଭାଗରେ କରାଯାଏ ?
Answer:
ପଶ୍ଚିମ
Question 8.
ଭାରତର ମୁଖ୍ୟ ଗହମ ଉତ୍ପାଦନ ଅଞ୍ଚଳର ନାମ କ’ଣ ?
Answer:
ଗଙ୍ଗା-ସତଲେଜ ସମତଳ ଅଞ୍ଚଳ
Question 9.
ଭାରତର ଶସ୍ୟାଗାର ଅଞ୍ଚଳରେ ଋଷ କରାଯାଉଥିବା ଶସ୍ୟର ନାମ କ’ଣ ?
Answer:
ଗହମ
Question 10.
କେଉଁ ଦେଶରେ କୃଷିକ ଏକ ଶିଳ୍ପ ରୂପେ ଗଣନା କରାଯାଏ ?
Answer:
ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା
ଭୌଗୋଳିକ ଶବ୍ଦଗୁଡ଼ିକୁ ଗୋଟିଏ ଗୋଟିଏ ବାକ୍ୟରେ ଲେଖ।
Question 1.
ରବି ଫସଲ :
Answer:
ଶୀତଋତୁରେ ବୁଣାଯାଇ ଗ୍ରୀଷ୍ମଋତୁ ଆରମ୍ଭରେ ଅମଳ କରାଯାଉଥିବା ଫସଲ ।
Question 2.
ଅର୍ଥକରୀ କୃଷି :
Answer:
ଅନ୍ୟ ଦେଶକୁ ରପ୍ତାନି କରିବା ଲକ୍ଷ୍ୟନେଇ କରାଯାଉଥିବା କୃଷି।
![]()
Question 3.
ଆର୍ଦ୍ର କୃଷି
Answer:
50 ସେ.ମି.ରୁ ଅଧିକ ବୃଷ୍ଟି ପାଉଥିବା ଅଞ୍ଚଳର କୃଷି ।
Question 4.
ପ୍ରୟୋଜନ ଭିଭିକ କୃଷି :
Answer:
ନିଜର ଚାହିଦା ପୂରଣ କରିବା ପାଇଁ ଜମିରୁ ଶସ୍ୟ ଉତ୍ପାଦନ ବ୍ୟବସ୍ଥା ।
Question 5.
ରୋପଣ କୃଷି :
Answer:
ଫସଲ ରୋପଣ କରାଯାଇ ହେଉଥିବା କୃଷି ।
Question 6.
ସଘନମିଶ୍ରିତ କୃଷି :
Answer:
ଫସଲ ଉତ୍ପାଦନ ସହିତ ପଶୁପାଳନ ।
Question 7.
ସ୍ଥାନାନ୍ତରିତ କୃଷି :
Answer:
ପୃଥିବୀର କ୍ରାନ୍ତୀୟ ଅଞ୍ଚଳରେ ଜଙ୍ଗଲ ପୋଡ଼ି ଓ ସଫା କରି କରାଯାଉଥିବା କୃଷି ।
Question 8.
ଝୁ ମ୍ ଚାଷ :
Answer:
ଉତ୍ତର-ପୂର୍ବ ପାର୍ବତ୍ୟ ଅଞ୍ଚଳରେ ଆଦିବାସୀ ଲୋକମାନଙ୍କଦ୍ୱାରା କରାଯାଉଥିବା କୃଷିକାର୍ଯ୍ୟ ।
Question 9.
ପୋଡ଼ୁ ଚାଷ :
Answer:
ଓଡ଼ିଶାର ସ୍ଥାନାନ୍ତରିତ କୃଷିର ଅନ୍ୟନାମ ।
Question 10.
ପୁନମ୍
Answer:
କେରଳରେ ସ୍ଥାନାନ୍ତରିତ କୃଷିର ଅନ୍ୟନାମ ।
Question 11.
ମିଶ୍ରିତ କୃଷି :
Answer:
ଖାଦ୍ୟଶସ୍ୟ ଉତ୍ପାଦନସହ ପଶୁପାଳନ ।
![]()
Question 12.
କଫି :
Answer:
ଆନାମାଲାଇ ଓ ମାଲାବାର ପାର୍ବତ୍ୟ ଅଞ୍ଚଳରେ ବ୍ୟାପକ ଭାବେ ଚାଷକରାଯାଉଥିବା ଏକ ଫସଲ ।
Question 13.
ସାଓପାଓଲୋ ମାଳ ଅଞ୍ଚଳ :
Answer:
ପୃଥିବୀର ବୃହତ୍ କଫିଚାଷ ଅଞ୍ଚଳ ।
Question 14.
ତାମିଲନାଡୁର ତ୍ରିକୋଣ ଭୂମି ଅଞ୍ଚଳ:
Answer:
ଭାରତର ପ୍ରାଚୀନତମ କପାଚାଷ ଅଞ୍ଚଳ ।
Question 15.
ଇଜିପ୍ଟ ବା ମିଶର :
Answer:
ଦୀର୍ଘ ତନ୍ତୁଯୁକ୍ତ କପା ଉତ୍ପାଦନକାରୀ ଅଗ୍ରଣୀ ଦେଶ ।
Question 16.
ଝୋଟ :
Answer:
ସ୍ଵତନ୍ତୁ ରୂପେ ପରିଚିତ ଏକ ତନ୍ତୁଜାତୀୟ ଫସଲ ।
Question 17.
ରାଜସ୍ଥାନ :
Answer:
ଭାରତରେ ବାଜରା ଉତ୍ପାଦନରେ ଅଗ୍ରଣୀ ରାଜ୍ୟ ।
Question 18.
ଚୀନ୍ :
Answer:
ଧାନ ଉତ୍ପାଦନରେ ପ୍ରଥମ ସ୍ଥାନ ଅଧିକାର କରିଥିବା ଦେଶ ।
Question 19.
ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା :
Answer:
ମକା ଉତ୍ପାଦନରେ ପୃଥମ ସ୍ଥାନ ଅଧିକାର କରିଥିବା ଦେଶ ।
Question 20.
ବାଜରା :
Answer:
ଅନୁର୍ବର ମୃରିକାରେ ହେଉଥିବା ଏକ ଖାଦ୍ୟଶସ୍ୟ ।
![]()
Question 21.
ସେଚିତ କୃଷି :
Answer:
ସ୍ୱଳ୍ପ ବୃଷ୍ଟିପାତ ହେଉଥବା ଅଞ୍ଚଳରେ ଜଳସେଚନଦ୍ଵାରା କରାଯାଉଥିବା କୃଷି ।
ଅସଂପର୍କିତ ଶବ୍ଦଟିକୁ ବାଛ ।
Question 1.
ମତ୍ସ୍ୟ ସଂଗ୍ରହ, ଜଙ୍ଗଲରୁ କାଠ, ଗହମରୁ ଅଟା, ମହୁ ସଂଗ୍ରହ ।
Answer:
ଗହମରୁ ଅଟା
Question 2.
ଧାନରୁ ଋଉଳ, ଧାତୁ ଉତ୍ତୋଳନ, ଆଖୁରୁ ଚିନି, ବାଉଁଶରୁ କାଗଜ ।
Answer:
ଧାତୁ ଉତ୍ତୋଳନ
Question 3.
କପାରୁ ଲୁଗା, ବ୍ୟାଙ୍କ, ବୀମା, ବାଣିଜ୍ୟ ।
Answer: କପାରୁ ଲୁଗା
Question 4.
ପଶୁପାଳନ, ମତ୍ସ୍ୟଋଷ, ମହୁଋଷ, ଖଣିଜ ଧାତୁ ଉତ୍ତୋଳନ।
Answer:
ଖଣିଜ ଧାତୁ | ଉତ୍ତୋଳନ
Question 5.
ବିହନ, ସୂର୍ଯ୍ୟାଲୋକ, ଉତ୍ତାପ, ବୃଷ୍ଟିପାତ।
Answer:
ବିହନ
Question 6.
କୃଷି ଯନ୍ତ୍ରପାତି, ବିହନ, ଶ୍ରମ, ମୃରିକା ।
Answer:
ମୁଭିକା
Question 7.
ଝୁମ୍, ପୁନମ୍, ରାଞ୍ଚି, ପୋଡୁ ।
Answer:
ରାଞ୍ଚ
![]()
Question 8.
ପଶୁଗରଣ, ମିଶ୍ରିତ କୃଷି, ସ୍ଥାନାନ୍ତରିତ କୃଷି, ସଘନ ପ୍ରୟୋଜନଭିଭିକ କୃଷି ।
Answer:
ପଶୁଚାରଣ
Question 9.
ଆମ୍ବ, ପଣସ, ରବର, କଦଳୀ ।
Answer:
ରବର
Question 10.
ଋହା, କଫି, ଆଖୁ, ନଡ଼ିଆ।
Answer:
ନଡ଼ିଆ
Question 11.
ଧାନ, କପା, ଗହମ, ବାଜରା ।
Answer: କପା
Question 12.
ମୁମ୍ବାଇ, ସୁରତ, ଗୁଡ଼ଗାଓଁ, ଅହମଦାବାଦ
Answer:
ଗୁଡ଼ଗାଓଁ
Question 13.
ପାନ, ନଡ଼ିଆ, ଆମ୍ବ, ଆଖୁ।
Answer:
ଆଖୁ
ଠିକ୍ ଉଢି ପାଖରେ ଠିକ୍ ଚିହ୍ନ ( ✓ ) ଭୁଲ୍ ଭକ୍ତ ପାଖରେ ଭୁଲ୍ ଚିହ୍ନ ( ✗ ) ଦିଅ।
1. କ୍ରାନ୍ତୀୟ ଓ ଉପକ୍ରାନ୍ତୀୟ ଅଞ୍ଚଳର ଲୋକମାନଙ୍କର ମୁଖ୍ୟ ଖାଦ୍ୟ ଗହମ । —- ଚିହ୍ନ ( ✗ )
2. ଝୋଟ ଋଷ ଆର୍ଦ୍ର କୃଷି ଅନ୍ତର୍ଗତ । —- ଠିକ୍ ( ✓ )
3. କେରଳରୁ ପାନ ବହୁଦେଶକୁ ରପ୍ତାନୀ କରାଯାଏ। —- ଚିହ୍ନ ( ✗ )
4. କୃଷିର ପ୍ରକ୍ରିୟା କରଣ କାରଖାନା ନିକଟସ୍ଥ କୃଷି ଭୂମିରେ ସ୍ଥାପନ କରାଯାଇଥାଏ । —- ଠିକ୍ ( ✓ )
5. କାଜୁ ଉଦ୍ୟାନ କୃଷିର ଅନ୍ତର୍ଭୁକ୍ତ । —- ଚିହ୍ନ ( ✗ )
6. ଉତ୍ତର-ପୂର୍ବ ଭାରତର ସ୍ଥାନାନ୍ତରିତ କୃଷିକୁ ରୋକା କୁହାଯାଏ । —- ଚିହ୍ନ ( ✗ )
7. ଚୀନ୍ ଏକ ବିକାଶୋନ୍ମୁଖୀ ଦେଶ। —- ଠିକ୍ ( ✓ )
8. ମହୁ ସଂଗ୍ରହ ଏକ ଦ୍ଵିତୀୟକ ପ୍ରକ୍ରିୟା। —- ଚିହ୍ନ ( ✗ )
![]()
Objective Type Questions With Answers
ସ୍ତମ୍ଭ ମିଳନ କର
Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

Question 4.

Answer:

![]()
Question 5.

Answer:

Question 6.

Answer:

Question 7.
Answer:

![]()
Question 8.

Answer:

Question 9.

Answer:

ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ଶବ୍ଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
1. ପୃଥିବୀର ଶତକଡ଼ା ______ ଭାଗ ଲୋକ କୃଷିକୁ ଜୀବିକା ରୂପେ ଗ୍ରହଣ କରିଛନ୍ତି ।
(୫୦%, ୫୫%, ୬୦%, ୬୫%)
Answer: ୬୫%
2. ଭାରତର ଦୁଇ-ତୃତୀୟାଂଶ ଲୋକ ________ କାର୍ଯ୍ୟରେ ନିୟୋଜିତ ହୋଇଥାନ୍ତି।
(ଶିଳ୍ପ, ଶିକ୍ଷା, କୃଷି, ସ୍ଵାସ୍ଥ୍ୟ)
Answer: କୃଷି
3. ________ ର ଉନ୍ନତି ଦେଶର ରାଜନୈତିକ, ସାମାଜିକ ତଥା ଅର୍ଥନୈତିକ ବିକାଶକୁ ପ୍ରଭାବିତ କରିଥାଏ।
(କୃଷି, ଶିକ୍ଷା, ପରିବହନ, ଯୋଗାଯୋଗ)
Answer: କୃଷି
![]()
4. ପ୍ରୟୋଜନଭିଭିକ କୃଷି _____ ଦେଶରେ ବିଶେଷଭାବେ ପ୍ରଚଳିତ।
(ଜାପାନ ଓ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ଚୀନ ଓ ଭାରତ, ଶ୍ରୀଲଙ୍କା ଓ ମିଆଁମାର, ଇଂଲଣ୍ଡ ଓ ଜର୍ମାନୀ)
Answer: ଚୀନ ଓ ଭାରତ
5. ଭାରତର _____ ରାଜ୍ୟରେ ଯାଯାବର ଶ୍ରେଣୀର ଲୋକମାନେ ପଶୁସ୍କରଣ କରୁଥିବାର ଦେଖାଯାଏ ।
(ଓଡ଼ିଶା ଓ ପଶ୍ଚିମବଙ୍ଗ, ଆସାମ ଓ ବିହାର, ଛତିଶଗଡ଼ ଓ ପଞ୍ଜାବ, ରାଜସ୍ଥାନ ଓ ଜାମ୍ମୁ-କାଶ୍ମୀର)
Answer: ରାଜସ୍ଥାନ ଓ ଜାମ୍ମୁ-କାଶ୍ମୀର
6. ‘ କର୍ଜନ ଓ ଦହନ’ _____ କୃଷିର ଅନ୍ତର୍ଗତ ।
(ପ୍ରୟୋଜନଭିଭିକ, ସ୍ଥାନାନ୍ତରିତ, ବାଣିଜ୍ୟଭିତ୍ୟିକ, ଅର୍ଥକରୀ)
Answer: ସ୍ଥାନାନ୍ତରିତ
7. ଦକ୍ଷିଣ ଆମେରିକାର ଆମାଜନ ନଦୀ ଅବବାହିକା ଓ ଆଫ୍ରିକାର କ୍ରାନ୍ତି ଅଞ୍ଚଳରେ __________ ପ୍ରକାର କୃଷି କାର୍ଯ୍ୟ କରାଯାଏ।
(ସ୍ଥାନାନ୍ତରିତ କୃଷି, ପ୍ରୟୋଜନଭିଭିକ କୃଷି, ସଘନ କୃଷି, ବ୍ୟାପକ କୃଷି)
Answer: ସ୍ଥାନାନ୍ତରିତ କୃଷି
8. ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଓ ଉତ୍ତର-ପୂର୍ବ ଭାରତର କେତେକାଞ୍ଚଳରେ __________ ପ୍ରକାର କୃଷି କାର୍ଯ୍ୟ କରାଯାଏ।
(ବାଣିଜ୍ୟଭିଭିକ, ପ୍ରୟୋଜନଭିଭିକ, ସଘନ, ସ୍ଥାନାନ୍ତରିତ)
Answer: ସ୍ଥାନାନ୍ତରିତ
9. ଓଡ଼ିଶାର ସ୍ଥାନାନ୍ତରିତ କୃଷିକୁ __________ କୁହାଯାଏ ।
(ପୋଡୁ, ଝୁମ୍, ପୁନମ୍, ରୋକା)
Answer: ପୋଡୁ
10. __________ କୁ ‘ସ୍ଵତନ୍ତୁ’ କୁହାଯାଏ।
(କପା, ଝୋଟ, ରେଶମ, ପଶମ)
Answer: ଝୋଟ
![]()
11. ପୃଥିବୀର __________ ଦେଶରେ ଝୋଟ ଋଷ ଅଧିକ ହୋଇଥାଏ।
(ଚୀନ ଓ ଇଣ୍ଡୋନେସିଆ, ପେରୁ ଓ ଚିଲି, ଭାରତ ଓ ବାଂଲାଦେଶ, ନାଇଜେରିଆ ଓ ଇଜିପ୍ଟ)
Answer: ଭାରତ ଓ ବାଂଲାଦେଶ
12. ପାହାଡ଼ର ଗଡାଣିଆ ଅଂଶରେ ଧାଡି ଧାଡ଼ି କରି __________ ଋଷ କରାଯାଇଥାଏ।
(ଧାନ, ଗହମ, ଝୋଟ, ସ୍କନ୍ଦା)
Answer: ସ୍କନ୍ଦା
13. ________ ଇଂରେଜମାନଙ୍କ ଦ୍ବାରା ସର୍ବପ୍ରଥମେ ଦେଶର ଉତ୍ତର- ପୂର୍ବ ଅଞ୍ଚଳରେ ପାର୍ବତ୍ୟ ଗଡାଣି ଆ ଭାଗରେ ଋହାଋଷ କରାଯାଇଥିଲା ।
(1829 ଖ୍ରୀ:ଅ., 1830 ଖ୍ରୀ:ଅ., 1831 ଖ୍ରୀ:ଅ.,1832 ଖ୍ରୀ:ଅ.)
Answer: 1829 ଖ୍ରୀ:ଅ
14. ଭାରତର ________ ରାଜ୍ୟର ପାର୍ବତ୍ୟାଞ୍ଚଳରେ ଋହା ବଗିରମାନ ଅଛି ।
(ଓଡ଼ିଶା ଓ ଆନ୍ଧ୍ର ପ୍ରଦେଶ, ଉତ୍ତରାଖଣ୍ଡ ଓ ହିମାଚଳ ପ୍ରଦେଶ, ଛତିଶଗଡ଼ ଓ ବିହାର, ଆସାମ ଓ ପଶ୍ଚିମବଙ୍ଗ)
Answer: ଆସାମ ଓ ପଶ୍ଚିମବଙ୍ଗ
15. ଦକ୍ଷିଣ ଭାରତର ________ ଅଞ୍ଚଳରେ ଋହାଋଷ କରାଯାଏ।
(ପୂର୍ବଘାଟ ଓ ପଶ୍ଚିମଘାଟ ପର୍ବତମାଳା, ନୀଳଗିରି ଓ କେରଳ, ତାମିଲନାଡୁ ଓ ପୂର୍ବଘାଟ, କର୍ଣାଟକ ଓ ପଶ୍ଚିମଘାଟ ପର୍ବତମାଳା)
Answer: ନୀଳଗିରି ଓ କେରଳ
16. ସମୁଦ୍ର ପତ୍ତନଠାରୁ 350 ମିଟରରୁ 1830 ମିଟର ଉଚ୍ଚତା ମଧ୍ୟରେ ________ ଋଷ କରାଯାଏ ।
(ଝୋଟ, ଆଖୁ, ଋହା, କଫି)
Answer: କଫି
17. ________ ଦେଶ କଫି ଋଷରେ ଅଗ୍ରଣୀ।
(ଭାରତ, ବ୍ରାଜିଲ, ବାଂଲାଦେଶ, କେନିଆ)
Answer: ବ୍ରାଜିଲ
![]()
18. ପୃଥିବୀରେ ଉତ୍ପନ୍ନ ହେଉଥିବା କଫି ଫସଲର ଶତକଡ଼ା ________ ଭାଗ ଭାରତରେ କରାଯାଏ ।
(ଏକ, ଦୁଇ, ତିନି, ଊରି)
Answer: ଊରି
19. _______ ମହାଦେଶରେ ଭାରତ କଫିର ଋହିଦା ଅଧ୍ବକ ।
(ଏସିଆ ଓ ଇଉରୋପ, ଇଉରୋପ ଓ ଅଷ୍ଟ୍ରେଲିଆ, ଉତ୍ତର ଆମେରିକା ଓ ଦକ୍ଷିଣ ଆମେରିକା, ଆଫ୍ରିକା ଓ ଏସିଆ)
Answer: ଇଉରୋପ ଓ ଅଷ୍ଟ୍ରେଲିଆ
20. _______ ରାଜ୍ୟରେ କଫିଋଷ କରାଯାଏ ନାହିଁ ।
(କର୍ଣ୍ଣାଟକ, ତାମିଲନାଡୁ, କେରଳ, ଆନ୍ଧ୍ରପ୍ରଦେଶ)
Answer: ଆନ୍ଧ୍ରପ୍ରଦେଶ
21. ଓଡ଼ିଶାର _______ ଠାରେ କଫିଋଷ କରାଯାଏ।
(କୋରାପୁଟ ଓ ନବରଙ୍ଗରପୁର, ରାୟଗଡ଼ା ଓ ବ୍ରହ୍ମପୁର, ଛତ୍ରପୁର ଓ ବାରିପଦା, ରାଉରକେଲା ଓ ଭଦ୍ରକ)
Answer: କୋରାପୁଟ ଓ ନବରଙ୍ଗରପୁର
22. _______ ନୁହେଁ ରାଷ୍ଟ୍ର ବାଣିଜ୍ୟଭିଭିକ କୃଷି ଉତ୍ପାଦନରେ ଅଗ୍ରଣୀ ରାଷ୍ଟ୍ର
(ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, କାନାଡା, ଶ୍ରୀଲଙ୍କା, ଇଉକ୍ରେନ)
Answer: ଶ୍ରୀଲଙ୍କା
23. ଭାରତର _______ ରାଜ୍ୟରେ ବ୍ୟାପକ ଭାବରେ ଗହମ ଋଷ କରାଯାଏ ।
(ପଞ୍ଜାବ ଓ ହରିଆଣା, ଗୁଜରାଟ ଓ ରାଜସ୍ଥାନ, ଉତ୍ତର ପ୍ରଦେଶ ଓ ଓଡ଼ିଶା, ଆସାମ ଓ ବିହାର )
Answer: ପଞ୍ଜାବ ଓ ହରିଆଣା
24. ଖାଦ୍ୟଶସ୍ୟ, ପଶୁଖାଦ୍ୟ ଉତ୍ପାଦନ ସହ ପଶୁପାଳନକୁ _______ କୃଷି କୁହାଯାଏ ।
(ପ୍ରୟୋଜନଭିଭିକ କୃଷି, ସ୍ଥାନାନ୍ତରିତ କୃଷି, ସଘନ ପ୍ରୟୋଜନଭିତ୍ତିକ କୃଷି, ମିଶ୍ରିତ କୃଷି)
Answer: ମିଶ୍ରିତ
25. _______ ଦେଶର ପଶୁସ୍କରଣ ଭୂମିକୁ ‘ରାଞ୍ଚ’ କୁହାଯାଏ।
(ଭାରତ, ନିଉଜିଲ୍ୟାଣ୍ଡ, ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, କାନାଡା)
Answer: ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା
26. ଭାରତର _______ ରହିବା ବିଦେଶରେ ରହିଛି।
(କଦଳୀ, ସପୁରୀ, ଆମ୍ବ, ନଡିଆ)
Answer: ଆମ୍ବ
27. ଓଡ଼ିଶାରୁ _______ ବହୁ ପରିମାଣରେ ଦେଶକୁ ରପ୍ତାନି କରାଯାଇଥାଏ ।
(ସପୁରୀ, ପାନ, ନଡ଼ିଆ, କଦଳୀ)
Answer: ପାନ
![]()
28. କେରଳରୁ _______ ବିଦେଶକୁ ରପ୍ତାନି କରାଯାଇଥାଏ।
(ନଡିଆ, ଆମ୍ବ, ପଣସ, କଦଳୀ)
Answer: ନଡିଆ
29. _______ ଦେଶ ଋହା ଋଷରେ ପୃଥିବୀରେ ଅଗ୍ରଣୀ ରାଷ୍ଟ୍ର ।
(ଭାରତ ଓ ଶ୍ରୀଲଙ୍କା, ଚୀନ ଓ ଜାପାନ, ନେପାଳ ଓ ପାକିସ୍ତାନ, ଜର୍ମାନୀ ଓ ଇଂଲଣ୍ଡ)
Answer: ଭାରତ ଓ ଶ୍ରୀଲଙ୍କା
30. _______ ଦେଶ କପ୍ତି ଉତ୍ପାଦନରେ ଅଗ୍ରଣୀ।
(କାନାଡା, ସୁଇଜରଲ୍ୟାଣ୍ଡ, ବ୍ରାଜିଲ, ଭାରତ)
Answer: ବ୍ରାଜିଲ
31. ମାଲୟେସିଆ _______ ରୋପଣ କୃଷି ପାଇଁ ପ୍ରସିଦ୍ଧ ।
(ଋହା, କଫି, ଆଖୁ, ରବର)
Answer: ରବର
32. ଆଖୁ ଋଷରେ _______ ଦେଶ ଅଗ୍ରଣୀ।
(ମାଲୟେସିଆ, କ୍ୟୁବା, ବ୍ରାଜିଲ, ଜାପାନ)
Answer: କ୍ୟୁବା
![]()
33. ଉତ୍ତର ଗୋଲାର୍ଦ୍ଧର ନାତିଶୀତୋଷ୍ଠ ଅଞ୍ଚଳରେ ପୃଥିବୀର ଶତକଡ଼ା _______ ଭାଗ ଗହମ ଉତ୍ପାଦନ ହୋଇଥାଏ।
(୬୦%, ୭୦%, ୮୦%, ୯୦%)
Answer: ୯୦%
34. ଧାନଋଷ ପାଇଁ _______ଡିଗ୍ରୀ ତାପମାତ୍ରା ଆବଶ୍ୟକ ହୋଇଥାଏ।
(୨୫° ରୁ ୩୦, ୨୬ ରୁ ୩୦,୨୭ ରୁ ୩୦, ୨୮° ରୁ ୩୦)
Answer: ୨୭ ରୁ ୩୦
35. ଧାନ ଉତ୍ପାଦନରେ _______ ଦେଶ ପୃଥିବୀରେ ପ୍ରଥମ ସ୍ଥାନ ଅଧିକାର କରିଅଛି ।
(ଭାରତ, ବାଂଲାଦେଶ, ଚୀନ, ଶ୍ରୀଲଙ୍କା)
Answer: ଚୀନ
36. _______ ଶସ୍ୟ ଉଭୟ ମନୁଷ୍ୟ ଖାଦ୍ୟ ଓ ପଶୁଖାଦ୍ୟ ରୂପେ ବ୍ୟବହାର କରାଯାଏ ।
(ଧାନ, ଗହମ, ଯଅ, ମକା),
Answer: ମକା
37. ମକା ଉତ୍ପାଦନରେ _______ ଦେଶ ପୃଥିବୀରେ ପ୍ରଥମ ସ୍ଥାନ ଅସ୍ଵୀକାର କରିଛି ।
(ଚୀନ, ଭରୁଗୁଏ, ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ବ୍ରାଜିଲ)
Answer: ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା
38. _______ ଦେଶ ମକା ଉତ୍ପାଦନରେ ପୃଥିବୀରେ ଦ୍ଵିତୀୟ ସ୍ଥାନ ଅଧିକାର କରିଛି ।
(ଆଲାସ୍କା, କଲମ୍ବିଆ, ଚିଲି, ଚୀନ)
Answer: ଚୀନ
39. ଓଡ଼ିଶାର ଗଞ୍ଜାମ, ଢେଙ୍କାନାଳ ଓ ଅନୁଗୁଳ ଜିଲ୍ଲାରେ _______ ଋଷ ଅଧିକ ହୁଏ।
(ଗହମ, ମକା, ଯଅ, ବାଜରା)
Answer: ମକା
![]()
40. ଭାରତର ________ ରାଜ୍ୟରେ ବାଜରା ଋଷ ଅଧ୍ବକ କରାଯାଏ ।
(ଓଡ଼ିଶା, ମଧ୍ୟପ୍ରଦେଶ, ଗୁଜରାଟ, ରାଜସ୍ଥାନ)
Answer: ରାଜସ୍ଥାନ
41. ________ ମୃତ୍ତିକାରେ କପାଋଷ ଅଧ୍ବକ ହୋଇଥାଏ।
(ପଟୁ, ଲାଟେରାଇଟ୍, କୃଷ୍ଣ, ଅରଣ୍ୟ)
Answer: କୃଷ୍ଣ
ସମ୍ଭାବ୍ୟ ଉତ୍ତର ବାଛି ଲେଖ ।
Question 1.
କେଉଁଟି ପ୍ରାଥମିକ ପ୍ରକ୍ରିୟାର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) ଶସ୍ୟ ଉତ୍ପାଦନ
(B) ମତ୍ସ୍ୟ ସଂଗ୍ରହ
(C) ବାଉଁଶରୁ କାଗଜ
(D) ଜଙ୍ଗଲରୁ କାଠ ସଂଗ୍ରହ
Answer:
(C) ବାଉଁଶରୁ କାଗଜ
Question 2.
କେଉଁଟି ପ୍ରାଥମିକ ପ୍ରକ୍ରିୟାର କ୍ରମ ଅଟେ ?
(A) ଫଳ, ଝୁଣା, ମହୁ ସଂଗ୍ରହ
(B) ଧାନରୁ ଋଜ୍ଜଳ, ଗହମରୁ ଅଟା, କପାରୁ ଲୁଗା
(C) ଆଖୁରୁ ଚିନି, ବାଉଁଶରୁ କାଗଜ, ତୈଳବୀଜରୁ ତୈଳ
(D) ଖଣିଜ ଦ୍ରବ୍ୟରୁ ଯନ୍ତ୍ରପାତି, ବ୍ୟାଙ୍କ, ବୀମା
Answer:
(A) ଫଳ, ଝୁଣା, ମହୁ ସଂଗ୍ରହ
Question 3.
କେଉଁଟି ଦ୍ଵିତୀୟକ ପ୍ରକ୍ରିୟାର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) ଧାନରୁ ଋଭଳ
(B) ଗହମରୁ ଅଟା
(C) ପଶୁପାଳନ
(D) ଆଖୁରୁ ଚିନି
Answer:
(C) ପଶୁପାଳନ
Question 4.
କେଉଁ ସ୍ତରଟି ତୃତୀୟକ ପ୍ରକ୍ରିୟା ଅଟେ ?
(A) ଧାନରୁ ଋଜ୍ଜଳ, ଗହମରୁ ଅଟା, ଆଖୁରୁ ଚିନି
(B) ଫଳ, ଝୁଣା, ମହୁ ସଂଗ୍ରହ
(C) ଶସ୍ୟ ଉତ୍ପାଦନ, ମତ୍ସ୍ୟସଂଗ୍ରହ, ପଶୁପାଳନ
(D) ପରିବହନ, ବ୍ୟାଙ୍କ, ବୀମା
Answer:
(D) ପରିବହନ, ବ୍ୟାଙ୍କ, ବୀମା
![]()
Question 5.
କେଉଁ ସ୍ତରଟି କୃଷିକାର୍ଯ୍ୟର ଅନ୍ତର୍ଗତ ?
(A) ପଶୁପାଳନ, ମତ୍ସ୍ୟଋଷ, ମହୁଋଷ
(B) ପରିବହନ, କଳକାରଖାନା, କୋଠାବାଡ଼ି
(C) ଜାହାଜନିର୍ମାଣ, ଯୋଗାଯୋଗ, ପରିବହନ
(D) ଶିଳ୍ପାୟନ, ଶିକ୍ଷା, ସ୍ୱାସ୍ଥ୍ୟ
Answer:
(A) ପଶୁପାଳନ, ମତ୍ସ୍ୟଋଷ, ମହୁଋଷ
Question 6.
କେଉଁଟି କୃଷି କାର୍ଯ୍ୟ ପାଇଁ ପ୍ରାକୃତିକ ପରିବେଶ ନୁହେଁ ?
(A) ସୌରତାପ
(B) ବୃଷ୍ଟିପାତ
(C) ଭୂମିର ଗଠନ
(D) ଶ୍ରମ
Answer:
(D) ଶ୍ରମ
Question 7.
କେଉଁଟି କୃଷି କାର୍ଯ୍ୟ ପାଇଁ ମାନବୀୟ ନିବେଶ ନୁହେଁ ?
(A) ବିହନ
(B) ମୃଭିକା
(C) କୃଷି ଯନ୍ତ୍ରପାତି
(D) ରାସାୟନିକ ସାର
Answer:
(B) ମୃଭିକା
Question 8.
କେଉଁଟି ପ୍ରୟୋଜନଭିଭିକ କୃଷିର ଲକ୍ଷଣ ନୁହେଁ ?
(A) ପୁରାତନ ପଦ୍ଧତିରେ ଋଷ
(B) କଳସେଚନର ଅଭାବ
(C) ଅର୍ଥକରୀ ଫସଲ ଉତ୍ପାଦନ
(D) ଋଷୀ ଗରିବ
Answer:
(C) ଅର୍ଥକରୀ ଫସଲ ଉତ୍ପାଦନ
![]()
Question 9.
ସ୍ଥାନାନ୍ତରିତ କୃଷି ଦୃଷ୍ଟିରୁ କେଉଁ ଯୋଡ଼ିଟି ଭିନ୍ନ ଅଟେ ?
(A) ଝୁମ୍ – ଉତ୍ତର-ପୂର୍ବ ଭାରତ
(B) ପୁନମ୍ – କେରଳ
(C) ଓଡ଼ିଶା – ଦହନ
(D) ରୋକା – ବ୍ରାଜିଲ
Answer:
(C) ଓଡ଼ିଶା – ଦହନ
Question 10.
କେଉଁଟି ସ୍ଥାନାନ୍ତରିତ କୃଷିର ମୁଖ୍ୟ ଋଷ ?
(A) ଧାନ ଓ ଗହମ
(B) ଋ ଓ କଫି
(C) ମକା ଓ ଦେଶୀଆଳୁ
(D) ଫୁଲ ଓ ଫଳ
Answer:
(C) ମକା ଓ ଦେଶୀଆଳୁ
Question 11.
ଛୋଟ ଛୋଟ ଜମିରେ ଉନ୍ନତ ବିହନ, ନିୟମିତ ଜଳସେଚନ, ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାଣରେ ସାର ପ୍ରୟୋଗ କରି ଅଧୁକ ଶ୍ରମିକ ଦ୍ଵାରା ଋଷ କରି ଅଧ୍ବକ ଫସଲ ଉତ୍ପାଦନକୁ କେଉଁ କୃଷି କୁହାଯାଏ ?
(A) ପ୍ରୟୋଜନ ଭିଭିକ କୃଷି
(B) ସଘନ ପ୍ରୟୋଜନଭିଭିକ କୃଷି
(C) ସ୍ଥାନାନ୍ତରିତ କୃଷି
(D) ଉଦ୍ୟାନ କୃଷି
Answer:
(B) ସଘନ ପ୍ରୟୋଜନଭିଭିକ କୃଷି
Question 12.
କେଉଁଟି ସଘନ ପ୍ରୟୋଜନଭିଭିକ କୃଷି ଅଞ୍ଚଳର ମୁଖ୍ୟ ଫସଲ ?
(A) ଧାନ
(B) ଗହମ
(C) ମକା
(D) ବାଜରା
Answer:
(A) ଧାନ
![]()
Question 13.
ନିମ୍ନୋକ୍ତ କେଉଁ ଦେଶରେ ସଘନ ପ୍ରୟୋଜନଭିତ୍ତିକ କୃଷିକାର୍ଯ୍ୟ କରାଯାଏ ?
(A) ଜାପାନ
(B) ଶ୍ରୀଲଙ୍କା
(C) ବାଙ୍ଗଲାଦେଶ
(D) ଭାରତ
Answer:
(D) ଭାରତ
Question 14.
କେଉଁ ସ୍ତରଟି ଭାରତର ମୁଖ୍ୟ କପାଋଷ ରାଜ୍ୟ ଅଟେ ?
(A) ମହାରାଷ୍ଟ୍ର, କର୍ଣାଟକ, ତାମିଲନାଡୁ
(B) ଓଡ଼ିଶା, ଆନ୍ଧ୍ରପ୍ରଦେଶ, ଆସାମ
(C) ବିହାର, ପଶ୍ଚିମବଙ୍ଗ, ତ୍ରିପୁରା
(D) ହରିୟାଣା, ପଞ୍ଜାବ, ଗୁଜରାଟ
Answer:
(A) ମହାରାଷ୍ଟ୍ର, କର୍ଣାଟକ, ତାମିଲନାଡୁ
Question 15.
କେଉଁ ସ୍ତରଟି ପୃଥିବୀର ଋହା ଉତ୍ପାଦନକାରୀ ରାଷ୍ଟ୍ର ଅଟେ ?
(A) ମିଶର, ଇଜିପ୍ଟ, ନିଉଜିଲ୍ୟାଣ୍ଡ, ବ୍ରାଜିଲ
(B) କାନାଡା, ମେକ୍ସିକୋ, କଲମ୍ବିଆ, ପେରୁ
(C) ଚୀନ, ଭାରତ, ଶ୍ରୀଲଙ୍କା, କେନିଆ
(D) ନେପାଳ, ପାକିସ୍ତାନ, ଆଫଗାନିସ୍ଥାନ, ଇରାକ
Answer:
(C) ଚୀନ, ଭାରତ, ଶ୍ରୀଲଙ୍କା, କେନିଆ
Question 16.
କେଉଁ କୃଷିକୁ ଅର୍ଥକରୀ କୃଷି କୁହାଯାଏ ?
(A) ପ୍ରୟୋଜନଭିଭିକ କୃଷି
(B) ସ୍ଥାନାନ୍ତରିତ କୃଷି
(C) ସଘନ ପ୍ରୟୋଜନଭିଭିକ କୃଷି
(D) ବାଣିଜ୍ୟଭିଭିକ କୃଷି
Answer:
(D) ବାଣିଜ୍ୟଭିଭିକ କୃଷି
![]()
Question 17.
କେଉଁଟି ଉଦ୍ୟାନ କୃଷିର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) ଧାନ
(B) କଦଳୀ
(C) ଆମ୍ବ
(D) ପଣସ
Answer:
(A) ଧାନ
Question 18.
କେଉଁଟି ରୋପଣ କୃଷିର ଅନ୍ତର୍ଗତ ନୁହେଁ ?.
(A) ଇହା
(B) କଫି
(C) ରବର
(D) ଗହମ
Answer:
(D) ଗହମ
Question 19.
କେଉଁଟି ଶୁଷ୍କ ଅଞ୍ଚଳର କୃଷି ନୁହେଁ ?
(A) ଯଅ
(C) ମାଣ୍ଡିଆ
(B) ବାଜରା
(D) ଧାନ
Answer:
(D) ଧାନ
Question 20.
କେଉଁଟି ଆର୍ଦ୍ର ଅଞ୍ଚଳର କୃଷି ଅଟେ ?
(A) ଯଅ ଓ ବାଜରା
(B) ବାଜରା ଓ ମାଣ୍ଡିଆ
(C) ଧାନ ଓ ନଳିତା
(D) ଧାନ ଓ ଗହମ
Answer:
(C) ଧାନ ଓ ନଳିତା
Question 21.
ଭାରତ, ବାଂଲାଦେଶ, ମିଆଁମାର ଦେଶରେ ବ୍ୟାପକ ଭାବରେ କେଉଁ କୃଷି କରାଯାଏ ?
(A) ଗୋପଣ
(B) ଶୁଷ୍କ
(C) ଆର୍ଦ୍ର
(D) ସେଚିତ
Answer:
(C) ଆର୍ଦ୍ର
![]()
Question 22.
ଭାରତର କେଉଁ ରାଜ୍ୟରେ ସେଚିତ ଜଳସେଚନଦ୍ୱାରା ଅଧିକ ପରିମାଣରେ ଫସଲ ଉତ୍ପାଦନ କରାଯାଏ ?
(A) ପଞ୍ଜାବ ଓ ହରିୟାଣା
(B) ଓଡ଼ିଶା ଓ ଆନ୍ଧ୍ରପ୍ରଦେଶ
(C) ବିହାର ଓ ଗୋଆ
(D) ପଶ୍ଚିମବଙ୍ଗ ଓ ଝାଡ଼ଖଣ୍ଡ
Answer:
(C) ଆର୍ଦ୍ର
Question 23.
କେଉଁ କ୍ରମଟି ପୃଥିବୀର ବିସ୍ତୃତ ଗହମ ଉତ୍ପାଦନ ଅଞ୍ଚଳ ଅଟେ ?
(A) ନାଇଜର, ଇଜିପ୍ଟ, କେନିଆ
(B) କାନାଡା, ଗ୍ରୀନଲ୍ୟାଣ୍ଡ, ହଲାଣ୍ଡ
(C) ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ଅଷ୍ଟ୍ରେଲିଆ, ରୁଷିଆ
(D) ଆଲାସ୍କା, ଦକ୍ଷିଣ ଆଫ୍ରିକା, ବ୍ରାଜିଲ
Answer:
(C) ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ଅଷ୍ଟ୍ରେଲିଆ, ରୁଷିଆ
Question 24.
ଭାରତର କେଉଁ ରାଜ୍ୟରେ ଗହମ ଉତ୍ପାଦନ ଅଧିକ କରାଯାଇଥାଏ ?
(A) ପଞ୍ଜାବ ଓ ହରିୟାଣା
(B) ତାମିଲନାଡୁ ଓ କେରଳ
(C) ବିହାର ଓ ଛତିଶଗଡ଼
(D) ତ୍ରିପୁରା ଓ ଆସାମ
Answer:
(A) ପଞ୍ଜାବ ଓ ହରିୟାଣା
Question 25.
ଧାନ ଋଷପାଇଁ କେତେ ବୃଷ୍ଟିପାତ ଆବଶ୍ୟକ ହୋଇଥାଏ ?
(A) ୧୦୦ ସେ.ମି.ରୁ ୨୦୦ ସେ.ମି.
(B) ୨୦୦ ସେ.ମି.ରୁ ୨୫୦ ସେ.ମି.
(C) ୨୦୦ ସେ.ମି.ରୁ ୩୦୦ ସେ.ମି.
(D) ୧୦୦ ସେ.ମି.ରୁ ୧୫୦ ସେ.ମି.
Answer:
(A) ପଞ୍ଜାବ ଓ ହରିୟାଣା
Question 26.
ଓଡ଼ିଶାର କେଉଁ ଜିଲ୍ଲାରେ ବାଜରା ଓ ମାଣିଆ ଋଷ କରାଯାଇଥାଏ ?
(A) ଗଜପତି ଓ ଗଞ୍ଜାମ
(B) କଟକ ଓ କେନ୍ଦ୍ରାପଡା
(C) ନୟାଗଡ଼ ଓ କନ୍ଧମାଳ
(D) ଭଦ୍ରକ ଓ ବାଲେଶ୍ଵର
Answer:
(A) ଗଜପତି ଓ ଗଞ୍ଜାମ
![]()
Question 27.
କେଉଁ ଦେଶର କପା ଦୀର୍ଘତନ୍ତୁ ଯୁକ୍ତ ଅଟେ ?
(A) ଇଜିପ୍ଟ
(C) ଉରୁଗୁଏ
(B) ପାରାନା ପାରାଗୁଏ
(D) ଆର୍ଜେଣ୍ଟିନା
Answer:
(A) ଇଜିପ୍ଟ
Question 28.
କେଉଁଟି ଭାରତର ପ୍ରାଚୀନତମ କପାଋଷ ଅଞ୍ଚଳ ?
(A) ଓଡ଼ିଶା
(B) ଆନ୍ଧ୍ରପ୍ରଦେଶ
(C) ତାମିଲନାଡୁ
(D) କେରଳ
Answer:
(C) ତାମିଲନାଡୁ
Question 29.
କେଉଁ ଦେଶର ସ୍ଥାନାନ୍ତରିତ କୃଷିକୁ ରୋକା କୁହାଯାଏ ?
(A) ବ୍ରାଜିଲ
(B) ଭାରତ
(C) କାନାଡ଼ା
(D) ଯୁକ୍ତରାଷ୍ଟ୍ର
Answer:
(A) ବ୍ରାଜିଲ
Question 30.
କେଉଁ ଦେଶ ଝୋଟ ଉତ୍ପାଦନରେ ଅଗ୍ରଣୀ ?
(A) କେନିଆ
(B) ଆର୍ଜେଣ୍ଟିନା
(C) ଉଗାଣ୍ଡା
(D) ବାଂଲାଦେଶ
Answer:
(D) ବାଂଲାଦେଶ
Question 31.
ନିମ୍ନୋକ୍ତ କେଉଁଟି ରବି ଫସଲର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) ଧାନ
(B) ମୁଗ
(C) ହରଡ଼
(D) ସୋରିଷ
Answer:
(A) ଧାନ
![]()
Question 32.
ଦାର୍ଜିଲିଂ ଚାହା ଚାଷ ଅଞ୍ଚଳ କେଉଁ ରାଜ୍ୟରେ ଅବସ୍ଥିତ ?
(A) ଆସାମ
(B) ପଶ୍ଚିମବଙ୍ଗ
(C) ମେଘାଳୟ
(D) ତାମିଲନାଡୁ
Answer:
(B) ପଶ୍ଚିମବଙ୍ଗ
Question 33.
କଫିଚାଷ ଅଞ୍ଚଳ ସାଓପାଓଲୋ କେଉଁ ଦେଶରେ ଅବସ୍ଥିତ ?
(A) ବ୍ରାଜିଲ
(B) ଭଗାଣ୍ଡା
(C) କେନିଆ
(D) ଆଙ୍ଗୋଲା
Answer:
(A) ବ୍ରାଜିଲ
Question 34.
କେଉଁଟି ଭାରତର ଏକ ପ୍ରଧାନ ପଣ୍ୟଦ୍ରବ୍ୟ ?
(A) ଚାହା
(B) କଫି
(C) ତୁଳା
(D) ଗହମ
Answer:
(A) ଚାହା
Question 35.
ପୋଡୁଚାଷ କେଉଁ କୃଷିର ଅନ୍ତର୍ଗତ ?
(A) ସ୍ଥାନାନ୍ତରିତ କୃଷି
(B) ସେଚିତ କୃଷି
(C) ଏକକ କୃଷି
(D) ଶୁଷ୍କ କୃଷି
Answer:
(A) ସ୍ଥାନାନ୍ତରିତ କୃଷି
Quiestion 36.
କେଉଁ ନଦୀକୂଳରେ ଅନେକ ଝୋଟକଳ ଅଛି ?
(A) ହୁଗୁଳି
(B) ଭାଗିରଥୀ
(C) ମହାନଦୀ
(D) ଯମୁନା
Answer:
(A) ହୁଗୁଳି
Question 37.
ପୃଥିବୀର କେଉଁ ଦେଶ ତୁଳା ଉତ୍ପାଦନରେ ଅଗ୍ରଣୀ ?
(A) ଭାରତ
(B) ଚୀନ୍
(C) ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା
(D) ଇଜିପ୍ଟ
Answer:
(D) ଇଜିପ୍ଟ
![]()
Question 38.
କେଉଁଟି ଏକ ଉଦ୍ୟାନ କୃଷି ?
(A) ଚାହାଚାଷ
(B) ପନିପରିବା ଚାଷ
(C) ଗୋପାଳନ
(D) ମାଛଚାଷ
Answer:
(B) ପନିପରିବା ଚାଷ
Question 39.
କେଉଁ ଚାଷଟି ଅନ୍ୟମାନଙ୍କଠାରୁ ଭିନ୍ନ ?
(A) ଧାନ
(B) ଗହମ
(C) ମକା
(D) କପା
Answer:
(D) କପା
Question 40.
ଉତ୍ତର-ପୂର୍ବ ଭାରତରେ କରାଯାଉଥିବା ସ୍ଥାନାନ୍ତରିତ କୃଷିର ନାମ କ’ଣ ?
(A) ଝୁମ୍
(B) ପୁନମ୍
(C) ପୋଡ଼ୁ
(D) ରୋକା
Answer:
(D) କପା
Question 41.
ପୁନମ୍ କେଉଁ ଅଞ୍ଚଳର ଏକ ସ୍ଥାନାନ୍ତରିତ କୃଷି ?
(A) କେରଳ
(B) ଓଡ଼ିଶା
(C) ବ୍ରାଜିଲ
(D) ଉତ୍ତର-ପୂର୍ବ ଭାରତ
Answer:
(A) କେରଳ
Question 42.
ସର୍ବପ୍ରଥମେ ଯେଉଁ ଦେଶରେ ଚାହା ଏକ ପାନୀୟରୂପେ ବ୍ୟବହାର ହୋଇଥିଲା ?
(A) ଆମେରିକା
(B) ପାକିସ୍ତାନ
(C) ଭାରତ
(D) ବୀନ୍
Answer:
(D) ବୀନ୍
![]()
Question 43.
କେଉଁଟି ପୃଥବୀର ସର୍ବାଧିକ ଲୋକଙ୍କର ପ୍ରଧାନ ଖାଦ୍ୟଶସ୍ୟ
(A) ଧାନ
(B) ଗହମ
(C) ଜଓ୍ବାର
(D) ମକା
Answer:
(B) ଗହମ