BSE Odisha 10th Class Maths Notes Geometry Chapter 1 ଜ୍ୟାମିତିରେ ସାଦୃଶ୍ୟ

Odisha State Board BSE Odisha 10th Class Maths Notes Geometry Chapter 1 ଜ୍ୟାମିତିରେ ସାଦୃଶ୍ୟ will enable students to study smartly.

BSE Odisha Class 10 Maths Notes Geometry Chapter 1 ଜ୍ୟାମିତିରେ ସାଦୃଶ୍ୟ

→ ଉପକ୍ରମଣିକା (Introduction):

• ବିଭିନ୍ନ ସମୟରେ ଆମେ କେତେକ ବସ୍ତୁ ବା ଚିତ୍ର ସଂସ୍ପର୍ଶରେ ଆସିଲା ବେଳେ ସେଥୁମଧ୍ୟରୁ କେତେକ ଏକାଭଳି ଦେଖାଯାଏ । ସେମାନଙ୍କର ଆକୃତି ସମାନ ଥ‌ିବା ବେଳେ ସେମାନଙ୍କ ଆକାର ସମାନ ନ ଥାଏ । କେତେକର ଆକାର ଓ ଆକୃତି ସମାନ ଥାଏ ।
• ଅଭିନ୍ନ ଆକୃତି ଥି ବସ୍ତୁ ଦୁଇଟି ବା ଚିତ୍ର ଦୁଇଟିକୁ ସଦୃଶ ବସ୍ତୁ ବା ସଦୃଶ ଚିତ୍ର (Similar Figures) କୁହାଯାଏ । ସଦୃଶ ହେବାର ଗୁଣକୁ ସାଦୃଶ୍ୟ (Similarity) କୁହାଯାଏ ।
• ଚିତ୍ର ଦୁଇଟିର ଆକାର ସମାନ ହେଉ ବା ଅସମାନ ହେଉ, ଯଦି ଉଭୟର ଆକୃତି ସମାନ ହୁଏ; ତେବେ ଚିତ୍ର ଦୁଇଟିକୁ ସଦୃଶ ଚିତ୍ର କୁହାଯାଏ ।
• ପୂର୍ବରୁ ପଢ଼ିଥିବା ସର୍ବସମତାରୁ ଜଣାପଡ଼େ ଯେ, ସର୍ବସମ ଚିତ୍ରଗୁଡ଼ିକ ସଦୃଶ ହୁଅନ୍ତି; କାରଣ ଏ କ୍ଷେତ୍ରରେ ଚିତ୍ରଗୁଡ଼ିକର ଆକାର ଏବଂ ଆକୃତି ସମାନ ହୋଇଥା’ନ୍ତି ।
• ସର୍ବସମ ଚିତ୍ରଗୁଡ଼ିକ ସଦୃଶ ହୁଅନ୍ତି; କିନ୍ତୁ ସଦୃଶ ଚିତ୍ରମାନ ସର୍ବସମ ନ ହୋଇ ପାରନ୍ତି ।

→ ଦୁଇଟି ସମଆକୃତି ବିଶିଷ୍ଟ ଚିତ୍ରର ଉଦାହରଣ :

• ଦୁଇଟି ଭିନ୍ନ ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ବୃତ୍ତ ।
• ଦୁଇଟି ଭିନ୍ନ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ବର୍ଗଚିତ୍ର ।
• ଦୁଇଟି ଭିନ୍ନ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ସମବାହୁ ତ୍ରିଭୁଜ ।

→ ଜ୍ୟାମିତିରେ ଅନୁପାତ ଓ ସମାନୁପାତ (Ratio and Proportion in Geometry) :
(i) a, b, c, d ଚାରୋଟି ଧନାତ୍ମକ ସଂଖ୍ୟା ଏବଂ ସେଗୁଡ଼ିକ ସମାନୁପାତୀ ହେଲେ a : b : : c : d ହୁଏ । ମନେକର ∆ ABC ର ଭୂମିର ଦୈର୍ଘ୍ୟ b₁ ଏକକ ଓ ଉଚ୍ଚତା h₁ ଏକକ ।
∆ ABC ର କ୍ଷେତ୍ରଫଳ = $\frac{1}{2}$b₁h₁ ବର୍ଗଏକକ ।

ମନେକର ∆ DEF ର ଭୂମିର ଦୈର୍ଘ୍ୟ b₂ ଏକକ ଓ ଉଚ୍ଚତା h₂ ଏକକ ।
∆ ABC ର କ୍ଷେତ୍ରଫଳ = $\frac{1}{2}$b₂h₂ ବର୍ଗଏକକ ।

ସିଦ୍ଧାନ୍ତ :

• ସମାନ ଉଚ୍ଚତା ବିଶିଷ୍ଠ ଦୁଇଟି ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳର ଉକ୍ତ ତ୍ରିଭୁଜଦ୍ବୟର ଅନୁରୂପ ଭୂମିର ଦୈର୍ଘ୍ୟର ଅନୁପାତ ସହ ସମାନ ।
• ଦୁଇଟି ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ ସମାନ ହେଲେ ତ୍ରିଭୁଜଦ୍ୱୟର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ, ଭକ୍ତ ତ୍ରିଭୁଜଦ୍ଵୟର ଅନୁରୂପ ଉଚ୍ଚତା ଦ୍ବୟର ଅନୁପାତ ସହ ସମାନ ।

(ii) ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ∆ ABD, ∆ ABC ଓ ∆ ADC ତିନୋଟି ତ୍ରିଭୁଜ ।
D ବିନ୍ଦୁ $\overline{\mathrm{BC}}$ ଉପରେ ଅବସ୍ଥିତ ଏବଂ B – D – C ।
∆ ABD, ∆ ABC & ∆ ACD ପ୍ରତ୍ୟେକର ଶୀର୍ଷ A ।
ଅର୍ଥାତ୍ ∆ ABC, ∆ ABD ଓ ∆ ADC ର ଉଚ୍ଚତା ସମାନ ।

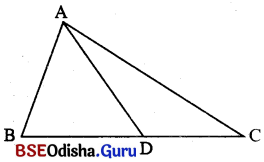
ଦୁଇଟି ବା ତତୋଽଧ୍ଵକ ତ୍ରିଭୁଜର ଭୂମିମାନ ଏକ ସରଳରେଖାରେ ରହିଲେ ଏବଂ ସେମାନଙ୍କର ଶୀର୍ଷବିନ୍ଦୁ ଅଭିନ୍ନ ହେଲେ ତ୍ରିଭୁଜଗୁଡ଼ିକ ସମ ଉଚ୍ଚତା ବିଶିଷ୍ଟ ହେବେ ।

→ ∆ ABCରେ $\overline{\mathrm{DE}}$ || $\overline{\mathrm{BC}}$ ରହଲେ D ବିନ୍ଦୁ $\overline{\mathrm{BC}}$ କୁ AD : DB ରେ ଏବଂ E ବିନ୍ଦୁ $\overline{\mathrm{BC}}$ କୁ AE : EC ରେ ଅନ୍ତର୍ବିଭକ୍ତ କରନ୍ତି ।
ଏଣୁ DB ଏହା ଆମେ ଉପପାଦ୍ୟ 1 ରୁ ପ୍ରମାଣ କରିପାରିବା ।

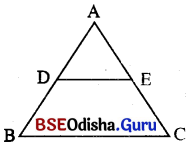
ଅର୍ଥାତ୍ ଏକ ତ୍ରିଭୁଜର ଗୋଟିଏ ବାହୁସହ ସମାନ୍ତର ଏକ ରେଖାଖଣ୍ଡ ଯଦି ତ୍ରିଭୁଜର ଅନ୍ୟ ଦୁଇବାହୁକୁ ଛେଦକରେ, ଉକ୍ତ ବାହୁଦ୍ୱୟ ଉପରେ ଉତ୍ପନ୍ନ ଛେଦିତାଂଶମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସମାନୁପାତୀ ହେବେ ।

ଉପପାଦ୍ୟ – 1 (ଥେଲିସ୍ ଉପପାଦ୍ୟ) :
ଏକ ତ୍ରିଭୁଜର ଗୋଟିଏ ବାହୁ ସହ ସମାନ୍ତର ଏକ ସରଳରେଖା ଯଦି ତ୍ରିଭୁଜର ଅନ୍ୟ ଦୁଇ ବାହୁକୁ ଦୁଇଟି ଭିନ୍ନ ବିନ୍ଦୁରେ ଛେଦକରେ, ତେବେ ଉକ୍ତ ସରଳରେଖା ଦ୍ୱାରା ଅନ୍ୟ ଦୁଇ ବାହୁ ସମାନୁପାତରେ ବିଭାଜିତ ହୁଅନ୍ତି ।

ମନ୍ତବ୍ୟ :
ଉପପାଦ୍ୟ 1 କୁ ଜ୍ୟାମିତିରେ ‘ମୌଳିକ ସମାନୁପାତିତା ଉପପାଦ୍ୟ’’ (Basic Proportionality theorem) କହନ୍ତି |
ଗ୍ରୀକ୍ ଦାର୍ଶନିକ ଓ ଗଣିତଜ୍ଞ ଥେଲିସଙ୍କ ନାମ ଅନୁସାରେ ଏହାକୁ ଥେଲିସ୍‌ଙ୍କ ଉପପାଦ୍ୟ କୁହାଯାଏ ।

ଉପପାଦ୍ୟ – 2 (ଉପପାଦ୍ୟ 1ର ବିପରୀତ ଉପପାଦ୍ୟ) :
ଏକ ତ୍ରିଭୁଜର ଦୁଇବାହୁକୁ ସମାନୁପାତରେ ଅନ୍ତର୍ବିଭାଜନ କରୁଥିବା ରେଖା, ଉକ୍ତ ତ୍ରିଭୁଜର ତୃତୀୟ ବାହୁ ସହ ସମାନ୍ତର ।
ମନ୍ତବ୍ୟ : କୌଣସି ରେଖା ଏକ ତ୍ରିଭୁଜର ଯେ କୌଣସି ଦୁଇଟି ବାହୁକୁ ସମାନୁପାତରେ ବହିର୍ବିଭାଜନ କଲେ, ଉକ୍ତରେଖା ତ୍ରିଭୁଜର ତୃତୀୟ ବାହୁ ସହ ସମାନ୍ତର ହେବ ।

→ ଛେଦକ ରେଖା ଓ ଛେଦିତାଂଶ (Transversal and Intercept) :
(i) ଦତ୍ତ ଚିତ୍ରରେ L₁ ଓ L₂ ରେଖାଦ୍ଵୟର $\overleftrightarrow{AB}$ ଏକ ଛେଦକ (transversal) | L₁ ଓ L₂ କୁ ଛେଦକ, $\overleftrightarrow{AB}$ ଯଥାକ୍ରମେ C ଓ D ବିନ୍ଦୁରେ ଛେଦକରେ । $\overline{\mathrm{CD}}$ କୁ ଛେଦକ $\overleftrightarrow{AB}$ ଉପରିସ୍ଥ ଛେଦିତାଂଶ (intercept) ବୋଲି କୁହାଯାଏ ।
(L₁ ଓ L₂ ପରସ୍ପର ସମାନ୍ତର ବା ଅସମାନ୍ତର ହୋଇପାରନ୍ତି ।)

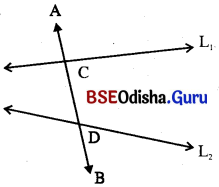
(ii) ସେହିପରି L₁ || L₂ ଏବଂ $\overleftrightarrow{AB}$, L₁ ଓ L₂ କୁ ଯଥାକ୍ରମେ C ଓ D ବିନ୍ଦୁରେ ଛେଦକଲେ $\overline{\mathrm{CD}}$ କୁ ଛେଦକ $\overleftrightarrow{AB}$ ଉପରିସ୍ଥ ଛେଦିତାଂଶ କୁହାଯାଏ ।

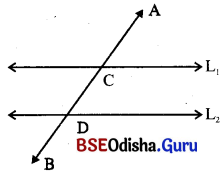
→ ତିନୋଟି ରେଖାର ଛେଦକ ଉପରିସ୍ଥ ଛେଦିତାଂଶ :
ମନେକର L₁, L₂ ଓ L₃ ତିନୋଟି ରେଖାକୁ ଏକ ଛେଦକ ‘T’ ଯଥାକ୍ରମେ A, B, C ବିନ୍ଦୁରେ ଛେଦକରେ ।
ଛେଦକ ରେଖା T ଉପରେ L₁ ଓ L₂ ଦ୍ବାରା ଉତ୍ପନ୍ନ ଛେଦିତାଂଶ AB, L₁ ଓ L₂ ଦ୍ବାରା ଉତ୍ପନ୍ନ ଛେଦିତାଂଶ $\overline{\mathrm{AC}}$ ଏବଂ L₁ ଓ L₂ ଦ୍ବାରା ଉତ୍ପନ୍ନ ଛେଦିତାଂଶ $\overline{\mathrm{BC}}$ ।

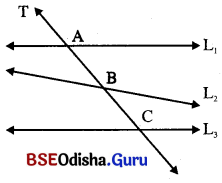
ଏକ ଛେଦକ ଉପରିସ୍ଥ ଦୁଇଟି ଛେଦବିନ୍ଦୁଦ୍ଵାରା ନିର୍ଦ୍ଧାରିତ ରେଖାଖଣ୍ଡକୁ ଛେଦକର ଗୋଟିଏ ଛେଦିତାଂଶ ବା ଛେକାଂଶ କୁହାଯାଏ ।

→ ତିନୋଟି ରେଖାର ଦୁଇଟି ଛେଦକ ଉପରିସ୍ଥ ଅନୁରୂପ ଛେଦିତାଂଶ :
ଏଠାରେ L₁, L₂ ଓ L₃ ତିନୋଟି ସରଳରେଖାକୁ T₁ ଓ T₂ ରେଖାଦ୍ଵୟ ଛେଦକରନ୍ତି । L₁, L₂ ଓ L₃ କୁ ଛେଦକ T₁ ଯଥାକ୍ରମେ A, B, C ବିନ୍ଦୁରେ ଏବଂ L₁, L₂ ଓ L₃ କୁ ଛେଦକ T₂ ଯଥାକ୍ରମେ D, E, F ବିନ୍ଦୁରେ ଛେଦକରେ ।

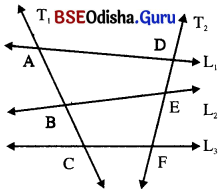
ଏଠାରେ T₁ ଓ T₂ ଛେଦକଦ୍ବୟ ଉପରେ ଉତ୍ପନ୍ନ ଛେଦିତାଂଶ ମଧ୍ୟରେ AB ଓ DE ଦୁଇଟି ଅନୁରୂପ ଛେଦିତାଂଶ । ସେହିପରି BC ଓ EF ଏବଂ AC ଓ DE ମଧ୍ୟ ଦୁଇଟି ଅନୁରୂପ ଛେଦିତାଂଶ ।

ଦୁଇଟି ସରଳରେଖାକୁ ଦୁଇଟି ଛେଦକ ଛେଦକଲେ, ଛେଦକ ରେଖାଦ୍ବୟ ଉପରେ ଉତ୍ପନ୍ନ ହୋଇଥିବା ଛେଦିତାଂଶ ଦ୍ଵୟକୁ ଅନୁରୂପ ଛେଦିତାଂଶ (corresponding intercepts) କୁହାଯାଏ ।

→ ପ୍ରଶ୍ନାବଳା ଓ ଉତ୍ତର

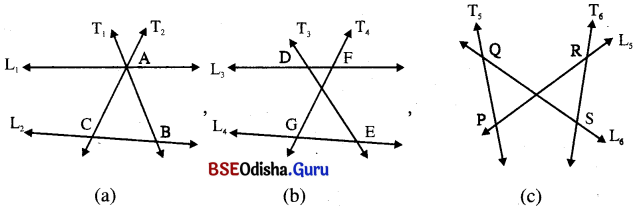
ପ୍ରଶ୍ନ – 1: ଚିତ୍ର (a) ରେ L₁ ଓ L₂ ରେଖାଦ୍ୱୟକୁ ଛେଦକ T₁ ଯଥାକ୍ରମେ ଓ B ବିନ୍ଦୁରେ ଏବଂ ଛେଦକ T₂ ଯଥାକ୍ରମେ A ଓ C ବିନ୍ଦୁରେ ଛେଦକରେ । ଏ କ୍ଷେତ୍ରରେ ଅନୁରୂପ ଛେଦିତାଂଶ ଦୁଇଟିର ନାମ କୁହ ।
ପ୍ରଶ୍ନ – 2: ଚିତ୍ର (b) ରେ L₃ ଓ L₄ ରେଖାଦ୍ୱୟକୁ ଛେଦକ T₃ ଯଥାକ୍ରମେ D ଓ E ବିନ୍ଦୁରେ ଏବଂ ଛେଦକ T₄ ଯଥାକ୍ରମେ F ଓ G ବିନ୍ଦୁରେ ଛେଦକରେ । ଏ କ୍ଷେତ୍ରରେ ଅନୁରୂପ ଛେଦିତାଂଶ ଦୁଇଟିର ନାମ କୁହ ।
ପ୍ରଶ୍ନ – 3 : ଚିତ୍ର (c) ରେ L₅ ଓ L₆ ରେଖାଦ୍ୱୟକୁ ଛେଦକ T₅ ଯଥାକ୍ରମେ P ଓ Q ବିନ୍ଦୁରେ ଏବଂ ଛେଦକ T₆ ଯଥାକ୍ରମେ R ଓ S ବିନ୍ଦୁରେ ଛେଦକରେ । ଏ କ୍ଷେତ୍ରରେ ଅନୁରୂପ ଛେଦିତାଂଶ ଦୁଇଟିର ନାମ କୁହ ।
ସମାଧାନ :
1. ଦୁଇଟି ଅନୁରୂପ ଛେଦିତାଂଶ $\overline{\mathrm{AC}}$ ଓ $\overline{\mathrm{AB}}$ ।
2. ଦୁଇଟି ଅନୁରୂପ ଛେଦିତାଂଶ $\overline{\mathrm{DE}}$ ଓ $\overline{\mathrm{FG}}$ ।
3. ଦୁଇଟି ଅନୁରୂପ ଛେଦିତାଂଶ $\overline{\mathrm{PQ}}$ ଓ $\overline{\mathrm{RS}}$ ।

→ ତିନୋଟି ସମାନ୍ତର ସରଳରେଖାର ଦୁଇଟି ଛେଦକ ଉପରିସ୍ଥ ଅନୁରୂପ ଛେଦିତାଂଶଟି ମଧ୍ଯରେ ସମ୍ପର୍କ :
ମନେକର L₁ || L₂ || L₃ ଏବଂ T₁ ଛେଦକ ଓ T₂ ଛେଦକ L₁, L₂ ଓ L₃ କୁ ଯଥାକ୍ରମେ A, B, C ଓ D, E, F ବିନ୍ଦୁରେ ଛେଦକରେ ।

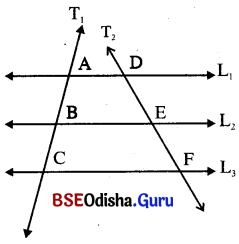
L₁ ଓ L₂ କୁ T₁ ଓ T₂ ଛେଦକରିବା ଦ୍ବାରା ଉତ୍ପନ୍ନ ଅନୁରୂପ ଛେଦିତାଂଶ $\overline{\mathrm{AB}}$ ଓ $\overline{\mathrm{DE}}$ ।

L₂ ଓ L₃ କୁ T₁ ଓ T₂ ଛେଦକରିବା ଦ୍ବାରା ଉତ୍ପନ୍ନ ଅନୁରୂପ ଛେଦିତାଂଶ $\overline{\mathrm{BC}}$ ଓ $\overline{\mathrm{EF}}$ ।

L₁ ଓ L₃ କୁ T₁ ଓ T₂ ଛେଦକରିବା ଦ୍ବାରା ଉତ୍ପନ୍ନ ଅନୁରୂପ ଛେଦିତାଂଶ $\overline{\mathrm{AC}}$ ଓ $\overline{\mathrm{DF}}$ ।

$\overline{\mathrm{AB}}$, $\overline{\mathrm{BC}}$, $\overline{\mathrm{AC}}$, $\overline{\mathrm{DE}}$, $\overline{\mathrm{EF}}$ ଓ $\overline{\mathrm{DF}}$ ର ଦୈର୍ଘ୍ୟକୁ ମାପିଲେ ଆମେ ଦେଖୁ ଯେ $\frac{A B}{D E}=\frac{B C}{E F}=\frac{A C}{D F}$ ହେବ ।

ତିନୋଟି ପରସ୍ପର ସମାନ୍ତର ସରଳରେଖାକୁ ଦୁଇଟି ଛେଦକ ରେଖା ଛେଦ କରିବାଦ୍ଵାରା ଛେଦକ ରେଖାଦ୍ୱୟ ଉପରେ ଉତ୍ପନ୍ନ ହୋଇଥିବା ଅନୁରୂପ ଛେଦିତାଂଶ ଗୁଡ଼ିକର ଦୈର୍ଘ୍ୟର ଅନୁପାତ ସମାନ ।

ପ୍ରମେୟ 1.1 :
ତିନୋଟି ପରସ୍ପର ସମାନ୍ତର ସରଳରେଖାକୁ ଦୁଇଟି ସରଳରେଖା ଛେଦକରିବା ଦ୍ଵାରା, ଛେଦକ ରେଖାଦ୍ୱୟ ଉପରେ ଉତ୍ପନ୍ନ ହୋଇଥିବା ଅନୁରୂପ ଛେଦିତାଂଶମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସମାନୁପାତା ହୁଅନ୍ତି ।
ଅନୁସିଦ୍ଧାନ୍ତ (i) (a) $\frac{AB}{BC}$ ⇒ $\frac{DF}{EF}$, (b) $\frac{BC}{AC}$ ⇒ $\frac{EF}{DF}$ (ଉପରିସ୍ଥ ଚିତ୍ର ଦେଖ ।)

ଅନୁସିଦ୍ଧାନ୍ତ (ii) : ତିନୋଟି (ବା ଅଧ‌ିକ ସଂଖ୍ୟକ) ସମାନ୍ତର ସରଳରେଖାକୁ ଛେଦ କରୁଥିବା ଗୋଟିଏ ଛେଦକ ଉପରିସ୍ଥ ଛେଦିତାଂଶମାନେ ସମଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ହେଲେ, ଉକ୍ତ ସମାନ୍ତର ସରଳରେଖାମାନଙ୍କର ଅନ୍ୟ ଯେକୌଣସି ଛେଦକ ଉପରିସ୍ଥ ଛେଦିତାଂଶମାନଙ୍କର ଦୈର୍ଘ୍ୟ ମଧ୍ୟ ସମାନ ।

ପ୍ରମେୟ : 1.1 ର ବିପରୀତ ଉକ୍ତି ସତ୍ୟ ନ ହୋଇପାରେ ।
ଅର୍ଥାତ୍ ତିନୋଟି ରେଖାକୁ ଦୁଇଟି ଛେଦକ ରେଖା ଛେଦକରିବା ଦ୍ଵାରା ଛେଦକ ରେଖାଦ୍ବୟ ଉପରେ ଉତ୍ପନ୍ନ ଅନୁରୂପ ଛେଦିତାଂଶମାନ ସମାନୁପାତୀ ହେଲେ, ଛେଦିତରେଖା ତିନୋଟି ସମାନ୍ତର ହୋଇପାରନ୍ତି ବା ନହୋଇପାରନ୍ତି ।

→ ତ୍ରିଭୁଜର କୋଣର ସମଦ୍ବିଖଣ୍ଡକ ସମ୍ବନ୍ଧୀୟ ଆଲୋଚନା
ଉପପାଦ୍ୟ – 3 :
ଗୋଟିଏ ତ୍ରିଭୁଜର ଏକ କୋଣର ସମଦ୍ୱିଖଣ୍ଡକ, ସେହି କୋଣର ସମ୍ମୁଖୀନ ବାହୁକୁ ଯେଉଁ ଦୁଇଟି ରେଖାଖଣ୍ଡରେ ଭାଗକରେ, ସେମାନଙ୍କର ଦୈର୍ଘ୍ୟର ଅନୁପାତ, ଅନୁରୂପ ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଅନୁପାତ ସଙ୍ଗେ ସମାନ ।

ପ୍ରମେୟ – 1.2: (ଉପପାଦ୍ୟ – 3 ର ବିପରୀତ କଥନ) :
ଏକ ତ୍ରିଭୁଜର କୌଣସି ଏକ କୋଣର ଶୀର୍ଷରୁ ଅଙ୍କିତ ରଶ୍ମି ଉକ୍ତ କୋଣର ବିପରୀତ ବାହୁକୁ ଯେଉଁ ଦୁଇଟି ଅଂଶରେ ଭାଗ କରେ, ସେ ଦୁଇଟିର ଦୈର୍ଘ୍ୟ, ଅନୁରୂପ ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସହ ସମାନୁପାତୀ ହେଲେ, ରଶ୍ମିଟି ସମ୍ପୃକ୍ତ କୋଣକୁ ସମଦ୍ଵିଖଣ୍ଡ କରେ ।

→ ତ୍ରିଭୁଜର ବହିଃସ୍ଥ କୋଣର ସମଦ୍ବିଖଣ୍ଡକ :

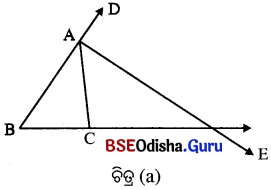
(i) ଚିତ୍ର (a)ରେ ∆ ABC ରେ ∠CAD ଏକ ବହିଃସ୍ଥ କୋଣ ଓ $\overrightarrow{AE}$, ∠CAD ର ସମଦ୍ବିଖଣ୍ଡକ ।
$\overrightarrow{AE}$ କୁ ∠BAC ର ଏକ ବହିଃ ସମଦ୍ବିଖଣ୍ଡକ କୁହାଯାଏ ।

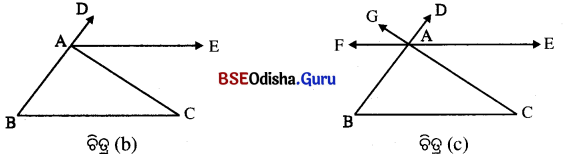
ଚିତ୍ର (b) ରେ $\overrightarrow{AE}$, ∠ABC ର ଏକ ବହିଃ ସମତ୍ତିଖଣ୍ଡକ ।
ଚିତ୍ର (c) ରେ $\overrightarrow{AE}$ ଓ $\overrightarrow{AF}$, ∠ABC ର ଦୁଇଟି ବହିଃ ସମଦ୍ବିଖଣ୍ଡକ ।
ଚିତ୍ର (a) ରେ AB > AC, ∠CAD ର ବହିଃସମଦ୍ଵିଖଣ୍ଡକ $\overrightarrow{AE}$ ।
ଚିତ୍ର (b) ରେ AC > AB, ∠CAD ର ବହିଃସମଦ୍ୱିଖଣ୍ଡକ $\overrightarrow{AE}$, $\overrightarrow{BC}$ ବା, $\overline{\mathrm{BC}}$ କୁ ଛେଦକରିବ ବୋଲି ଡୁନାହିଁ ।
ଚିତ୍ର (c) ରେ AB = AC, ∆ ABC ର ବହିଃସମଦ୍ବିଖଣ୍ଡକ ଦ୍ବୟ $\overrightarrow{AE}$ ଓ $\overrightarrow{AF}$, $\overline{BC}$ ସହ ସମାନ୍ତର । ଏଣୁ ତାହା $\overline{BC}$, $\overrightarrow{BC}$ ବା $\overrightarrow{CB}$ କାହାରିକୁ ଛେଦକରିବ ନାହିଁ ।

(ii) ମନେକର ∆ ABC ରେ AC > AB ।

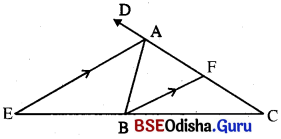
ବହିସ୍ଥ ∠BADର ସମଦ୍ବିଖଣ୍ଡକ, $\overrightarrow{CB}$ କୁ E ବିନ୍ଦୁରେ ଛେଦକରୁଛି ।
ଏଠାରେ $\overrightarrow{AE}$, $\overline{CB}$ କୁ E ବିନ୍ଦୁରେ ବହିଁବିଭାଜନ କରିଛି ବୋଲି କୁହାଯାଏ । $\overline{CB}$ ର ବହିଁବିଭାଜନର ଦୁଇଟି ଅଂଶ $\overline{CE}$ ଓ $\overline{BE}$ 1 B ବିନ୍ଦୁଠାରେ $\overline{AE}$ ସହ ସମାନ୍ତରଭାବେ ଅଙ୍କିତ ରେଖା $\overline{AC}$ କୁ F ବିନ୍ଦୁରେ ଛେଦକରୁ ।
$\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{BE}}{\mathrm{CE}}$

(iii) ∆ ABC, $\overrightarrow{CB}$ ଉପରେ E ଏପରି ଏକ ବିନ୍ଦୁ ଯେପରି C – B – E ଓ EB : EC = AB : AC ହେଲେ ∆ BAD କୁ $\overline{AE}$ ସମଦ୍ବିଖଣ୍ଡ କରେ ।

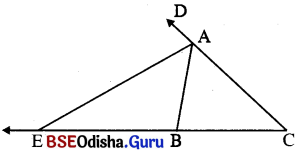
ଏକ ତ୍ରିଭୁଜର ଦୁଇବାହୁର ଦୈର୍ଘ୍ୟର ଅନୁପାତରେ ତୃତୀୟ ବାହୁକୁ ବହିଁବିଭାଜନ କରୁଥିବା ବିନ୍ଦୁ ଓ ଏହି ବାହୁର ବିପରୀତ ଶୀର୍ଷବିଦୁର ସଂଯୋଜକ ରେଖାଖଣ୍ଡ ଦ୍ବାରା ସେହି ଶୀର୍ଷରେ ଥ‌ିବା ବହିଃସ୍ଥକୋଣ ସମର୍ଦ୍ଦିଖଣ୍ଡିତ ହୁଏ ।

→ ଜ୍ୟାମିତିକ ଚିତ୍ର ମଧ୍ୟରେ ସାଦୃଶ୍ୟ (Similarity in Geometrical Figures) :

(i) ଦୁଇଟି ଜ୍ୟାମିତିକ ଚିତ୍ରର ଆକୃତି ତଥା ଆକାର ଉଭୟ ଅଭିନ୍ନ ହେଲେ ସେ ଦୁଇଟିକୁ ସର୍ବସମ ଚିତ୍ର (Congruent figure) କହନ୍ତି ।
(ii) ଦୁଇଟି ଜ୍ୟାମିତିକ ଚିତ୍ରର ଆକାର ସମାନ ବା ଅସମାନ ହେଉ, ଯଦି ଉଭୟ ଚିତ୍ରର ଆକୃତି ସମାନ ହୁଏ ତେବେ ଚିତ୍ର ଦୁଇଟିକୁ ସଦୃଶ ଚିତ୍ର (Similar figure) କହନ୍ତି ।
ଉଦାହରଣ ସ୍ୱରୂପ, ଭିନ୍ନ ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ବୃତ୍ତ, ଭିନ୍ନ ବାହୁବିଶିଷ୍ଟ ବର୍ଗଚିତ୍ର, ସମବାହୁ ତ୍ରିଭୁଜ ଇତ୍ୟାଦି ।

• ଦୁଇଟି ସଦୃଶ ଚିତ୍ର ସର୍ବସମ ନହୋଇପାରନ୍ତି ମାତ୍ର ଦୁଇଟି ସର୍ବସମ ଚିତ୍ର ସର୍ବଦା ସଦୃଶ ଅଟନ୍ତି ।
• ଦୁଇଟି ସମାନ ସଂଖ୍ୟକ ବାହୁ ବିଶିଷ୍ଟ ସୁଷମ ବହୁଭୁଜ ସର୍ବଦା ସଦୃଶ ।

→ ସଦୃଶ ବହୁଭୁଜ (Similar Polygons) :
ସମାନ ସଂଖ୍ୟକ ବାହୁଥ‌ିବା ଦୁଇଟି ବହୁଭୁଜ ସଦୃଶ ହେବେ ଯଦି ସେମାନଙ୍କର –
(i) ଅନୁରୂପ କୋଣମାନେ ସର୍ବସମ ଏବଂ
(ii) ଅନୁରୂପ ବାହୁମାନେ ସମାନୁପାତୀ ବିଶିଷ୍ଟ ।

→ ତ୍ରିଭୁଜମାନଙ୍କ ମଧ୍ୟରେ ସାଦୃଶ୍ୟ (Similarity in Triangles) :
ଯଦି ଦୁଇଟି ତ୍ରିଭୁଜର ଅନୁରୂପ ବାହୁମାନ ସମାନୁପାତୀ ଓ ଅନୁରୂପ କୋଣମାନ ସର୍ବସମ ହେବେ, ତେବେ ତ୍ରିଭୁଜଦ୍ଵୟ ସଦୃଶ ହେବେ ।

→ ସଦୃଶ ତ୍ରିଭୁଜ କ୍ଷେତ୍ରରେ ଅନ୍ୟାନ୍ୟ ଅନୁରୂପ ଅଙ୍ଗ :

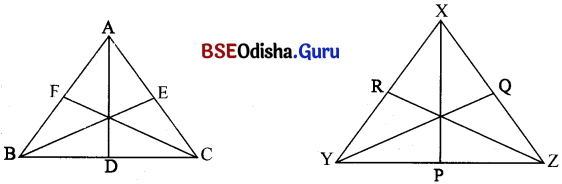
ମନେକର ∆ ABC ~ ∆ XYZ.
∆ ABC 66 $\overline{\mathrm{AD}} \perp \overline{\mathrm{BC}}, \overline{\mathrm{BE}} \perp \overline{\mathrm{AC}}$ ଓ $\overline{\mathrm{CF}} \perp \overline{\mathrm{AB}}$
∆ XYZ 66 $\overline{\mathrm{XP}} \perp \overline{\mathrm{YZ}}, \overline{\mathrm{YQ}} \perp \overline{\mathrm{XZ}}$ ଓ $\overline{\mathrm{ZR}} \perp \overline{\mathrm{XY}}$
$\overline{\mathrm{AD}}$ ଓ $\overline{\mathrm{XP}}$ ଅନୁରୂପ ଉଚ୍ଚତା । ସେହିପରି $\overline{\mathrm{BE}}$ ଓ $\overline{\mathrm{YQ}}$ ଅନୁରୂପ ଉଚ୍ଚତା । CF ଓ ZR ଅନୁରୂପ ଉଚ୍ଚତା ।

∆ ABC ରେ $\overline{\mathrm{BC}}$ ର ମଧ୍ୟବିନ୍ଦୁ P ଓ $\overline{\mathrm{EF}}$ ର ମଧ୍ୟବିନ୍ଦୁ Q ହେଲେ $\overline{\mathrm{AP}}$ ର ଅନୁରୂପ ମଧ୍ୟମା $\overline{\mathrm{DQ}}$ ।
ସେହିପରି ∠Aର ସମଦ୍ବିଖଣ୍ଡକ $\overline{\mathrm{AX}}$ ଓ ∠D ର ସମଦ୍ଵିଖଣ୍ଡକ DY ହେଲେ $\overline{\mathrm{AX}}$ ଓ $\overline{\mathrm{DY}}$ ତୁଭୁଜଦ୍ଵୟର ଅନୁରୂପ କୋଣ ସମଦ୍ଵିଖଣ୍ଡକ ।

→ ତ୍ରିଭୁଜର ସଦୃଶ୍ୟ ସମ୍ବନ୍ଧୀୟ ଧର୍ମ (Conditions on Triangle-Similarity) :
(i) ପ୍ରତ୍ୟେକ ତ୍ରିଭୁଜ ନିଜସହ ସଦୃଶ ଅର୍ଥାତ୍ ∆ ABC ~ ∆ ABC (ସୁତୁଲ୍ୟ ନିୟମ) ।
(ii) ∆ ABC ~ ∆ PQR ⇔ ∆ PQR ~ ∆ ABC (ପ୍ରତିସମ ନିୟମ) ।
(iii) ABC ~ ∆ DEF, ∆ DEF ~ ∆ POR ∆ ∆ ABC ~ ∆ POR (ସଂକ୍ରମୀ ନିୟମ) ।

→ ତ୍ରିଭୁଜର ସାଦୃଶ୍ୟ ସମ୍ବନ୍ଧୀୟ ସର୍ଭ :
(1) ଅନୁରୂପ ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟର ସମାନୁପାତିତା ।
(2) ଅନୁରୂପ କୋଣମାନଙ୍କର ସର୍ବସମତା ।

ବି.ଦ୍ର.: (i) ଯେକୌଣସି ଦୁଇଟି ଚତୁର୍ଭୁଜର ଅନୁରୂପ ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟର ସମାନୁପାତିତା ଏବଂ ଅନୁରୂପ କୋଣମାନଙ୍କର ସର୍ବସମତା ପରସ୍ପର ନିର୍ଭରଶୀଳ ନୁହନ୍ତି । ସେ ଦୁଇଟି ସର୍ଭ ପରସ୍ପର ନିରପେକ୍ଷ ।
(ii) ଦୁଇଟି ତ୍ରିଭୁଜ ମଧ୍ୟରେ ଅନୁରୂପ ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟର ସମାନୁପାତିତା ଏବଂ ଅନୁରୂପ କୋଣମାନଙ୍କର
ସର୍ବସମତା ସର୍ଭେଦ୍ଵୟ ପରସ୍ପର ନିର୍ଭରଶୀଳ । ଅର୍ଥାତ୍ ଗୋଟିଏ ସର୍ଭେ ସ୍ବତଃ ହେଲେ ଅନ୍ୟଟି ମଧ୍ୟ ସ୍ବତଃସିଦ୍ଧ ହୁଏ ।

ଉପପାଦ୍ୟ – 4 : ଗୋଟିଏ ତ୍ରିଭୁଜର ତିନିକୋଣ, ଅନ୍ୟ ଏକ ତ୍ରିଭୁଜର ଅନୁରୂପ କୋଣ ସହ ସର୍ବସମ ହେଲେ, ତ୍ରିଭୁଜ ଦୁଇଟି ସଦୃଶ ହୁଅନ୍ତି । (କୋ-କୋ-କୋ ସାଦୃଶ୍ୟ)

1. ଅନୁସିଦ୍ଧାନ୍ତ (1) : ଗୋଟିଏ ତ୍ରିଭୁଜର ଦୁଇଟି କୋଣ ଯଥାକ୍ରମେ ଅନ୍ୟ ଏକ ତ୍ରିଭୁଜର ଦୁଇଟି କୋଣ ସହ ସର୍ବସମ ହେଲେ, ତୃତୀୟ କୋଣ ଦ୍ଵୟ ସ୍ବତଃ ସର୍ବସମ ହୁଅନ୍ତି । (‘: ପ୍ରତ୍ୟେକ ତ୍ରିଭୁଜର ତିନିକୋଣର ପରିମାଣ ସମଷ୍ଟି 180° ।)
   ଏଣୁ ଏ କ୍ଷେତ୍ରରେ ତ୍ରିଭୁଜଦ୍ଵୟ ମଧ୍ଯ ସଦୃଶ ହୁଅନ୍ତି । ସାଦୃଶ୍ୟର ଏହି ସର୍ଭକୁ ସଂକ୍ଷେପରେ ‘କୋ-କୋ ସାଦୃଶ୍ୟ’ କୁହାଯାଏ ।
2. ଅନୁସିଦ୍ଧାନ୍ତ (2) : ସଦୃଶକୋଣୀ ତ୍ରିଭୁଜ ଦ୍ଵୟ (ଗୋଟିକର ତିନିକୋଣ ଯଥାକ୍ରମେ ଅନ୍ୟଟିର ତିନିକୋଣ ସହ ସର୍ବସମ)ର ଅନୁରୂପ ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସମାନୁପାତୀ ।

ଉପପାଦ୍ୟ – 5 : ଗୋଟିଏ ତ୍ରିଭୁଜର ତିନି ବାହୁର ଦୈର୍ଘ୍ୟ, ଅନ୍ୟ ଏକ ତ୍ରିଭୁଜର ଅନୁରୂପ ତିନିବାହୁର ଦୈର୍ଘ୍ୟ ସହ ସମାନୁପାତୀ ହେଲେ, ତ୍ରିଭୁଜ ଦୁଇଟି ସଦୃଶ ହୁଅନ୍ତି । (ବା-ବା-ବା ସାଦୃଶ୍ୟ)
ଉପପାଦ୍ୟ – 6 : ଗୋଟିଏ ତ୍ରିଭୁଜର ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟ, ଅନ୍ୟ ଏକ ତ୍ରିଭୁଜର ଅନୁରୂପ ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟ ସହ ସମାନୁପାତୀ ହେଲେ ଏବଂ ବାହୁମାନଙ୍କ ଅନ୍ତର୍ଗତ କୋଣ ଦୁଇଟି ସର୍ବସମ ହେଲେ, ତ୍ରିଭୁଜଦ୍ଵୟ ସଦୃଶ ହୁଅନ୍ତି । (ବା-କୋ-ବା ସାଦୃଶ୍ୟ)

ପ୍ରମେୟ – 1.3 : ଦୁଇଟି ସଦୃଶ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ, ସେମାନଙ୍କର ଅନୁରୂପ ବାହୁମାନଙ୍କ ଦୈର୍ଘ୍ୟର ବର୍ଗାନୁପାତ ସହ ସମାନ ।

ପ୍ରମେୟ 1.4 :
ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜର ସମକୋଣର ଶୀର୍ଷରୁ କର୍ଷ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ ଦ୍ୱାରା ଯେଉଁ ଦୁଇଟି ତ୍ରିଭୁଜ ଉତ୍ପନ୍ନ ହୁଏ, ସେ ଦ୍ଵୟ ପ୍ରତ୍ୟେକ ମୂଳ ତ୍ରିଭୁଜ ସହିତ ସଦୃଶ ଓ ପରସ୍ପର ସଦୃଶ ।
∆ ABC ର ∠ABC ସମକୋଣ ଏବଂ BD ⊥ AC ହେଲେ
(a) AB² = AD. AC, (b) BC² = CD. AC ଏବଂ (c) BD² = AD. DC

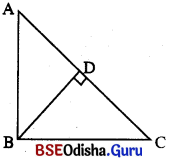
→ ଦୁଇଟି ସମକୋଣୀ ତ୍ରିଭୁଜ ମଧ୍ୟରେ ସାଦୃଶ୍ୟ :
ଦୁଇଟି ସମକୋଣୀ ତ୍ରିଭୁଜ ମଧ୍ୟରେ ଗୋଟିକର କଣ୍ଠ ଓ ଏକ ବାହୁର ଦୈର୍ଘ୍ୟ ଅନ୍ୟ ତ୍ରିଭୁଜର କର୍ଣ୍ଣ ଓ ଏକ ବାହୁର ଦୈର୍ଘ୍ୟ ସହ ସମାନୁପାତ୍ରୀ ହେଲେ, ତ୍ରିଭୁଜ ଦ୍ଵୟ ସଦୃଶ ଅଟନ୍ତି ।