BSE Odisha 10th Class Maths Notes Geometry Chapter 3 ବୃତ୍ତର ସ୍ପର୍ଶକ

Odisha State Board BSE Odisha 10th Class Maths Notes Geometry Chapter 3 ବୃତ୍ତର ସ୍ପର୍ଶକ will enable students to study smartly.

BSE Odisha Class 10 Maths Notes Geometry Chapter 3 ବୃତ୍ତର ସ୍ପର୍ଶକ

→ ଉପକ୍ରମଣିକା (Introduction) :
(i) ଚିତ୍ର- 1 ରେ ABC ଏକ ବୃତ୍ତ ଏବଂ L ଏକ ରେଖା । ଏଠରେ L ଓ ବୃତ୍ତ ମଧ୍ୟରେ କୌଣସି ସାଧାରଣ ବିନ୍ଦୁ ନାହିଁ । ଏଠାରେ ବୃତ୍ତ ଓ ସରଳରେଖା L ଅଣଛେଦୀ ।

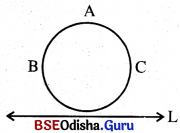
( ଚିତ୍ର-1 )
(ii) ଚିତ୍ର-2 ରେ ABC ବୃତ୍ତ ଓ L ରେଖା ମଧ୍ୟରେ ଦୁଇଟି ସାଧାରଣ ବିନ୍ଦୁ B ଓ C ରହିଛି ।
ଏ କ୍ଷେତ୍ରରେ ସରଳରଖା L ଓ ବୃତ୍ତ ABC ପରସ୍ପରଛେଦୀ । Lକୁ ଛେଦକ ରେଖା (secant) ଓ B, C ବିନ୍ଦୁକୁ ଛେଦବିନ୍ଦୁ କୁହାଯାଏ ।

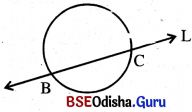
(ଚିତ୍ର-2)
(iii) ଚିତ୍ର-3ରେ L ରେଖା ଓ ବୃତ୍ତ ABC ପରସ୍ପରଛେଦୀ । ମାତ୍ର ସେମାନଙ୍କର ଗୋଟିଏ ମାତ୍ର ସାଧାରଣ ବିନ୍ଦୁ ରହିଛି । ଏ କ୍ଷେତ୍ରରେ L ରେଖାକୁ ବୃତ୍ତର ସ୍ପର୍ଶକ (tangent) ଓ P ବିନ୍ଦୁକୁ Lର ସ୍ପର୍ଶବିନ୍ଦୁ କୁହାଯାଏ ।

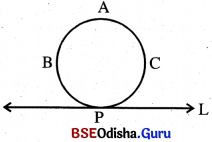
(ଚିତ୍ର-3)
ଏକ ସମତଳରେ ଅବସ୍ଥିତ ଏକ ବୃତ୍ତ ଓ ଏକ ସରଳରେଖାର ଗୋଟିଏ ମାତ୍ର ସାଧାରଣ ବିନ୍ଦୁ (ବା ଛେଦବିନ୍ଦୁ) ଥିଲେ ଉକ୍ତ ସରଳରେଖାକୁ ବୃତ୍ତର ଏକ ସ୍ପର୍ଶକ କୁହାଯାଏ ଏବଂ ସେମାନଙ୍କର ସାଧାରଣ ବିନ୍ଦୁକୁ ସଂପୃକ୍ତ ସ୍ପର୍ଶକର ସ୍ପର୍ଶବିନ୍ଦୁ କୁହାଯାଏ ।

(iv) ବୃତ୍ତର କେନ୍ଦ୍ର ଓ ସ୍ପର୍ଶବିନ୍ଦୁକୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡକୁ ସ୍ପର୍ଶବିନ୍ଦୁଗାମୀ ବ୍ୟାସାର୍ଦ୍ଧ କୁହାଯାଏ ।
କୌଣସି ବୃତ୍ତର ଏକ ସ୍ପର୍ଶକର ସ୍ପର୍ଶବିନ୍ଦୁ ବ୍ୟତୀତ ଅନ୍ୟ ସମସ୍ତ ବିନ୍ଦୁ ବୃତ୍ତର ବହିଃସ୍ଥ ଅଟନ୍ତି ।

ଉପପାଦ୍ୟ – 12
ଗୋଟିଏ ବୃତ୍ତର ଏକ ସ୍ପର୍ଶକ ଏହାର ସ୍ପର୍ଶବିଦୁଗାମୀ ବ୍ୟାସାର୍ଦ୍ଧ ପ୍ରତି ଲମ୍ବ ।

ପ୍ରମେୟ 3.1 : (ଉପପାଦ୍ୟ 12ର ବିପରୀତ କଥନ) : ବୃତ୍ତର କୌଣସି ବିଦୁରେ, ଉକ୍ତ ବିନ୍ଦୁଗାମୀ ବ୍ୟାସାର୍ଦ୍ଧ ପ୍ରତି ଲମ୍ବ, ଉକ୍ତ ବୃତ୍ତର ଏକ ସ୍ପର୍ଶକ ଅଟେ ।
ଅନୁସିଦ୍ଧାନ୍ତ 1 : ଏକ ବୃତ୍ତର କୌଣସି ଏକ ସ୍ପର୍ଶକର ସ୍ପର୍ଶବିନ୍ଦୁଠାରେ ଉକ୍ତ ସ୍ପର୍ଶକ ପ୍ରତି ଲମ୍ବ, କେନ୍ଦ୍ରବିନ୍ଦୁଗାମୀ ହେବ ।
ଅନୁସିଦ୍ଧାନ୍ତ 2 : ଏକ ବୃତ୍ତର କୌଣସି ଏକ ବିନ୍ଦୁଠାରେ ଗୋଟିଏ ଏବଂ କେବଳ ଗୋଟିଏ ସ୍ପର୍ଶକ ଅଙ୍କିତ ହୋଇପାରିବ ।
ଗୋଟିଏ ତ୍ରିଭୁଜ ABC ଦତ୍ତ ଥିଲେ ଏହାର ପ୍ରତ୍ୟେକ ବାହୁକୁ ସ୍ପର୍ଶ କରୁଥିବା କେବଳ ଗୋଟିଏ ମାତ୍ର ବୃତ୍ତ POR ନିର୍ଣ୍ଣୟ କରାଯାଇ ପାରିବ । ଉକ୍ତ ବୃତ୍ତକୁ ତ୍ରିଭୁଜର ଅନ୍ତଃବୃତ୍ତ (Incircle) କୁହାଯାଏ । P, Q ଓ R କୁ ସ୍ପର୍ଶବିନ୍ଦୁ କୁହାଯାଏ । ଅନ୍ତଃବୃତ୍ତର କେନ୍ଦ୍ରକୁ ଅନ୍ତଃକେନ୍ଦ୍ର (Incentre) କୁହାଯାଏ ।

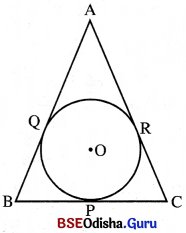
\(\overline{\mathrm{OA}}\), \(\overline{\mathrm{OB}}\) ଓ \(\overline{\mathrm{OC}}\) ଯଥାକ୍ରମେ ∠A, ∠B ଓ ∠Cର ସମଦ୍ବିଖଣ୍ଡକ ହେବେ ।

→ ବୃତ୍ତର ବହିଃସ୍ଥ ବିନ୍ଦୁରୁ ବୃତ୍ତପ୍ରତି ସ୍ପର୍ଶକ :
(i) ପାର୍ଶ୍ବରେ ABC ଏକ ବୃତ୍ତ । ଏହାର ବହିଃସ୍ଥ P ଏକ ବିନ୍ଦୁ P ବିନ୍ଦୁରୁ ଅନେକ ସରଳରେଖା ଅଙ୍କନ କଲେ ସେଥୁରୁ ଅନେକ ରେଖା ବୃତ୍ତକୁ ଦୁଇଟି ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
ଅନେକ ରେଖା ବୃତ୍ତକୁ ଆଦୌ ଛେଦ କରିବ ନାହିଁ । ମାତ୍ର ଦୁଇଟି ରେଖା ବୃତ୍ତକୁ ସ୍ପର୍ଶ କରିବ ।

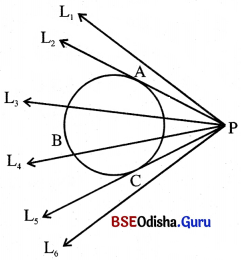
(ii) ଗୋଟିଏ ବୃତ୍ତର ବହିଃସ୍ଥ କୌଣସି ବିନ୍ଦୁରୁ ଉକ୍ତ ବୃତ୍ତପ୍ରତି ଦୁଇଟି ଏବଂ କେବଳ ଦୁଇଟି ସ୍ପର୍ଶକ ଅଙ୍କନ ସମ୍ଭବ ।
ସ୍ପର୍ଶକର ସ୍ପର୍ଶବିନ୍ଦୁ ଓ ବହିଃସ୍ଥ ବିନ୍ଦୁକୁ ଯୋଗକରୁ ଥ‌ିବା ରେଖାଖଣ୍ଡକୁ ସ୍ପର୍ଶକଖଣ୍ଡ (Tangent segment) କୁହାଯାଏ ।

ଉପପାଦ୍ୟ – 13 :
କୌଣସି ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁରୁ ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ ।
ଅନୁସିଦ୍ଧାନ୍ତ 1 : କୌଣସି ବୃତ୍ତର ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ P ଠାରୁ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡ \(\overline{\mathrm{PQ}}\) ଓ \(\overline{\mathrm{PR}}\) ହେଲେ ଏବଂ O ବୃତ୍ତର କେନ୍ଦ୍ର ହେଲେ \(\overline{\mathrm{PO}}\), ∠QPR ଓ ∠QORକୁ ସମନ୍ଦିଖଣ୍ଡ କରେ ।

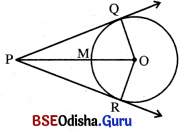
ଅନୁସିଦ୍ଧାନ୍ତ 2 : କୌଣସି ବୃତ୍ତର ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ P ଠାରୁ ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ \(\overline{\mathrm{PQ}}\) ଓ \(\overline{\mathrm{PR}}\) ହେଲେ ଏବଂ ୦ ବୃତ୍ତର କେନ୍ଦ୍ର ହେଲେ \(\overline{\mathrm{PO}}\), \(\widehat{\mathbf{Q R}}\) ଚାପକୁ ସମସ୍ଵିଖଣ୍ଡକ କରେ । ଅର୍ଥାତ୍‌ \(\widehat{\mathbf{Q M}}\) ≅ \(\widehat{\mathbf{R M}}\) ⇒ \(\overline{\mathrm{QM}}\) ≅ \(\overline{\mathrm{RM}}\) ।

→ ଏକାନ୍ତର ଚାପ (Alternate arc) :
(i) ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ABC ବୃତ୍ତର – ବିନ୍ଦୁରେ ବୃତ୍ତପ୍ରତି \(\overleftrightarrow{PQ}\) ସ୍ପର୍ଶକ ଅଙ୍କିତ ।
\(\overline{\mathrm{TA}}\) ଏକ ଜ୍ୟା ।
\(\overline{\mathrm{TA}}\) ଜ୍ୟାକୁ \(\overleftrightarrow{PQ}\) ସ୍ପର୍ଶକର ସ୍ପର୍ଶବିନ୍ଦୁଗାମୀ ଜ୍ୟା କୁହାଯାଏ ।

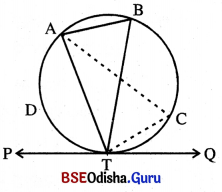
(ii) \(\overline{\mathrm{TA}}\) ଜ୍ଯା \(\overleftrightarrow{PQ}\) ସହ ∠ATP ଓ ∠ATQ ଅଙ୍କନ କରେ ।
ଜ୍ୟା \(\overline{\mathrm{TA}}\) ଦ୍ଵାରା ବୃତ୍ତ ABC ରେ ଦୁଇଟି ଚାପ \(\widehat{\mathbf{A B T}}\) ଓ \(\widehat{\mathbf{A D T}}\) ଉତ୍ପନ୍ନ ହୁଏ ।
\(\overline{\mathrm{TA}}\) ଜ୍ୟାର P ଯେଉଁ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ, B ବିନ୍ଦୁ ତା’ର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ । ଏଠାରେ \(\widehat{\mathbf{A B T}}\) କୁ ∠ATPର ଏକାନ୍ତର ଚାପ କହନ୍ତି ।
ଏହି ଚାପର ଅନ୍ତର୍ଲିଖ୍ ∠ABT କୁ ∠ATPର ଏକାନ୍ତର ଚାପାନ୍ତର୍ଲିଖ କୋଣ କୁହାଯାଏ ।
∠ACT ମଧ୍ଯ ∠ATPର ଅନ୍ୟ ଏକ ଏକାନ୍ତର ଚାପାନ୍ତର୍ଲିଖ କୋଣ ।
∠ATQ ର ଏକାନ୍ତର ଚାପ \(\widehat{\mathbf{A D T}}\) ଓ ଏକ ଏକାନ୍ତର ଚାପାନ୍ତର୍ଲିଖ କୋଣ ∠ADT ।

ପ୍ରମେୟ 3.2 :
ବୃତ୍ତର ଏକ ସ୍ପର୍ଶକ, ଏହାର ସ୍ପର୍ଶବିଦୁଗାମୀ କୌଣସି ଏକ ଜ୍ୟା ସହିତ ଯେଉଁ କୋଣ ଉତ୍ପନ୍ନ କରେ, ତା’ର ପରିମାଣ ସହ ଉକ୍ତ କୋଣର ଏକାନ୍ତର ଚାପାନ୍ତର୍ଲିଖ କୋଣର ପରିମାଣ ସମାନ ।

ପ୍ରମେୟ 3.3 : (ପ୍ରମେୟ 3.2ର ବିପରୀତ କଥନ)
ଏକ ବୃତ୍ତର କୌଣସି ଜ୍ୟା, ଏହାର ଏକ ପ୍ରାନ୍ତବିନ୍ଦୁ ଦେଇ ଅଙ୍କିତ ଏକ ସରଳରେଖା ସହ ଯେଉଁ କୋଣ ଅଙ୍କନ କରେ, ତାହା ଉକ୍ତ କୋଣର ଏକାନ୍ତର ଚାପାନ୍ତର୍ଲିଖ କୋଣ ସହ ସମପରିମାଣ ବିଶିଷ୍ଟ ହେଲେ, ସରଳରେଖାଟି ବୃତ୍ତପ୍ରତି ଏକ ସ୍ପର୍ଶକ ହେବ ।

→ ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ ଦେଇ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ଛେଦକ :

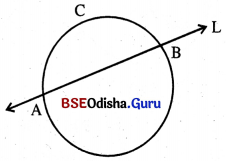
L ରେଖା ABC ବୃତ୍ତର ଏକ ଛେଦକ ରେଖା ।
L ରେଖା ABC ବୃତ୍ତକୁ ଦୁଇଟି ବିନ୍ଦୁ A ଓ Bରେ ଛେଦ କରୁଛି ।
A ଓ Bର ମଧ୍ୟବର୍ତୀ ସମସ୍ତ ବିନ୍ଦୁ ଭିନ୍ନ Lରେଖା ଉପରିସ୍ଥ ଅନ୍ୟ ସମସ୍ତ ବିନ୍ଦୁ ବୃତ୍ତ ABCର ବହିଃସ୍ଥ ।
ଏହିଭଳି ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁରୁ ABC ବୃତ୍ତପ୍ରତି ଅସଂଖ୍ୟ ଛେଦକ ରେଖାମାନ ଅଙ୍କନ କରାଯାଇ ପାରିବ ।

ଉପପାଦ୍ୟ 14 :
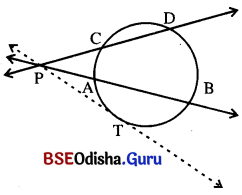
ଏକ ବୃତ୍ତର ବହିଃସ୍ଥ କୌଣସି ଏକ ବିନ୍ଦୁ P ଦେଇ ବୃତ୍ତପ୍ରତି ଏକ ସ୍ପର୍ଶକଖଣ୍ଡ \(\overline{\mathrm{PT}}\) ଏବଂ ଏକ ଛେଦକ \(\overleftrightarrow{PAB}\)
ଅଙ୍କିତ ଛେଦକ PA × PB = PT² ।
ଅନୁସିଦ୍ଧାନ୍ତ 1 :
ଏକ ବୃତ୍ତର ବହିଃସ୍ଥ କୌଣସି ଏକ ବିନ୍ଦୁ P ଦେଇ ଦୁଇଟି ଛେଦକ ଯଦି ବୃତ୍ତକୁ ଯଥାକ୍ରମେ A, B ଓ C, D ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି, ତେବେ ସ୍ପର୍ଶକ \(\overleftrightarrow{PT}\) (ସ୍ପର୍ଶ ବିନ୍ଦୁ T) ଅଙ୍କନ କରି ପ୍ରମାଣ
∴ PA × PB = PC × PD

→ ଏକାଧିକ ବୃତ୍ତ ସମ୍ବନ୍ଧୀୟ କେତେକ ତଥ୍ୟ :
ଏକ ସମତଳରେ S₁ ଓ S₂ ଦୁଇଟି ବୃତ୍ତ ।
(i) ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ର (କ) ଓ (ଖ)ରେ S₁ ଓ S₂ ଦୁଇଟି ଅଣଛେଦୀ ବୃତ୍ତ ।
(ii) ଚିତ୍ର (ଗ)ରେ S₁ ଓ S₂ ପରସ୍ପରକୁ ଦୁଇଟି ବିନ୍ଦୁରେ ଏବଂ ଚିତ୍ର (ଘ) ଓ (ଙ)ରେ ପରସ୍ପରକୁ ଗୋଟିଏ ବିନ୍ଦୁରେ ଛେଦ କରୁଛନ୍ତି ।

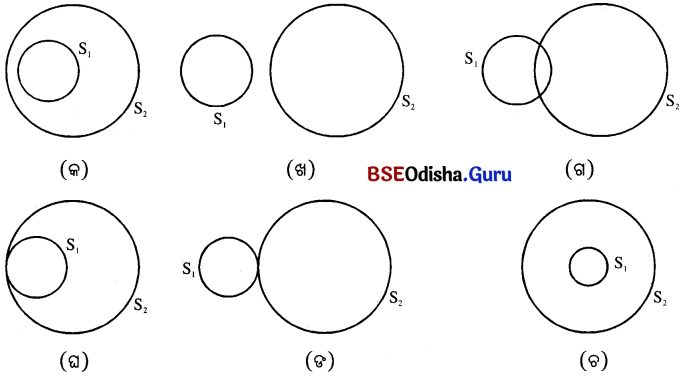
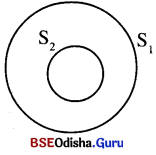
(iii) ଚିତ୍ର (ଚ)ରେ ଉଭୟ ବୃତ୍ତର କେନ୍ଦ୍ର ଅଭିନ୍ନ କିନ୍ତୁ ବ୍ୟାସାର୍ଦ୍ଧ ଭିନ୍ନ । ଏହି ବୃତ୍ତ ଦ୍ଵୟକୁ ଏକ-କେନ୍ଦ୍ରିକ (Concentric) ବୃତ୍ତ କୁହାଯାଏ । S₁ ଓ S₂ ବୃତ୍ତଦ୍ଵୟ ଏବଂ S₁ ବୃତ୍ତର ବହିର୍ଦେଶରେ ଥ‌ିବା S₂ ବୃତ୍ତର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍‌କୁ ବୃତ୍ତାକାର ବଳୟ (Circular annulus) କୁହାଯାଏ । ଏକ ବୃତ୍ତାକୃତି ବଳୟରେ ବହିଃସ୍ଥ ବୃତ୍ତର ଅନ୍ତର୍ଦେଶ ଓ ଅନ୍ତଃସ୍ଥ ବୃତ୍ତର ବହିର୍ଦ୍ଦେଶର ଛେଦଦ୍ୱାରା ଗଠିତ କ୍ଷେତ୍ରକୁ ବଳୟାକୃତି କ୍ଷେତ୍ର (Annular Region) କୁହାଯାଏ ।
(iv) ପାର୍ଶ୍ଵସ୍ଥ ଚିତ୍ରରେ S₁ ଓ S₂ ବୃତ୍ତଦ୍ଵୟ ପରସ୍ପରକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରୁଛନ୍ତି । \(\overleftrightarrow{AB}\) ସରଳରେଖାକୁ ଏହି ବୃତ୍ତଦ୍ଵୟର ରାଡ଼ିକାଲ ଅକ୍ଷ (Radical axis) କୁହାଯାଏ । \(\overline{PT}\) ରେଖାଖଣ୍ଡକୁ ବୃତ୍ତଦ୍ଵୟର ସାଧାରଣ ଜ୍ୟା (common chord) କୁହାଯାଏ ।

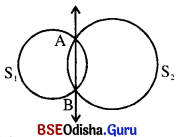
(ରାଡ଼ିକାଲ୍ ଅକ୍ଷ ଉପରିସ୍ଥ ଯେକୌଣସି ବିନ୍ଦୁରୁ ବୃତ୍ତଦ୍ଵୟ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଦ୍ଵୟର ଦୈର୍ଘ୍ୟ ସମାନ ।)

→ ସାଧାରଣ ସ୍ପର୍ଶକ (Common Tangents) :
ଏକ ସମତଳରେ ଥିବା ଦୁଇଟି ବୃତ୍ତକୁ ସେହି ସମତଳରେ ଯେଉଁ ସରଳରେଖା ବୃତ୍ତଦ୍ଵୟକୁ ସ୍ପର୍ଶକରେ ତାହାକୁ ଉକ୍ତ ବୃତ୍ତଦ୍ବୟର ଏକ ସାଧାରଣ ସ୍ପର୍ଶକ (Common tangent) କୁହାଯାଏ ।

(a) ପରସ୍ପର ଅଣଛେଦୀ ବୃତ୍ତର ସାଧାରଣ ସ୍ପର୍ଶକ :
ଚିତ୍ର (a) ଓ (b) ପ୍ରତ୍ୟେକରେ ଦୁଇଟି ଅଣଛେଦୀ ତଥା ପରସ୍ପର ବହିଃସ୍ଥ ବୃତ୍ତର ଚିତ୍ର ଦର୍ଶାଯାଇଛି । ଚିତ୍ର (a)ରେ ଥିବା S₁ ଓ S₂ ଉଭୟ ବୃତ୍ତକୁ L₁ ସରଳରେଖା ସ୍ପର୍ଶ କରୁଛି । ବୃତ୍ତ ଦ୍ବୟର କେନ୍ଦ୍ର O₁ ଓ O₂ ଉଭୟ L₁ ରେଖାରେ ଗୋଟିଏ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ । ଏପରିସ୍ଥଳେ L₁ ରେଖାକୁ ବୃତ୍ତଦ୍ଵୟର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ (direct common tangent) କୁହାଯାଏ । L₂ ରେଖା ମଧ୍ୟ ଚିତ୍ର (a)ରେ ଥ‌ିବା ବୃତ୍ତ ଦ୍ବୟର ଅନ୍ୟ ଏକ ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ । ଏଣୁ ଏକ ସମତଳରେ ଅବସ୍ଥିତ ଦୁଇଟି ଅଣଛେଦୀ ତଥା ପରସ୍ପର ବହିଃସ୍ଥ ବୃତ୍ତର ଦୁଇଗୋଟି ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ଥାଏ (ଚିତ୍ର (a)) ।

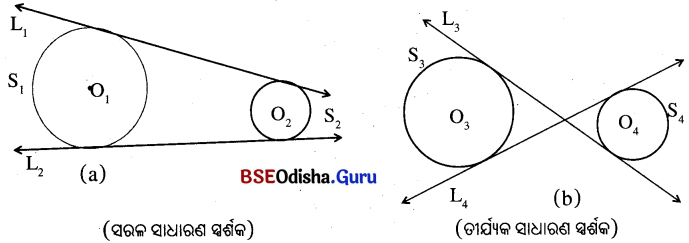
ଚିତ୍ର (b)ରେ ଥ‌ିବା S₃ ଓ S₄ ବୃତ୍ତ ଦ୍ଵୟକୁ L₃ ସରଳରେଖା ସ୍ପର୍ଶକ କରୁଛି ଏବଂ କେନ୍ଦ୍ର O₃ ଏବଂ O₄, L₃ ରେଖାର ବିପରୀତ ପାର୍ଶ୍ବରେ ଅଛନ୍ତି । ଏପରି କ୍ଷେତ୍ରରେ, ବୃତ୍ତ ଦ୍ବୟର ସାଧାରଣ ସ୍ପର୍ଶକକୁ ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ asi (transverse common tangent) |
ଦୁଇଟି ଅଣଛେଦୀ ତଥା ପରସ୍ପର ବହିଃସ୍ଥ ବୃତ୍ତ ଲାଗି ଦୁଇଟି ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକ ଥାଏ । (ଚିତ୍ର (b)

ଚିତ୍ରରେ ଦୁଇଟି ଅଣଛେଦୀ ବୃତ୍ତ Sã ଓ S, ମଧ୍ୟରୁ S, ବୃତ୍ତ S, ବୃତ୍ତର ଅନ୍ତଃସ୍ଥ । ଏଣୁ ଏପରି କ୍ଷେତ୍ରରେ କୌଣସି ସାଧାରଣ ସ୍ପର୍ଶକ ରହିବା

(b) ସ୍ପର୍ଶକ ବୃତ୍ତର ସାଧାରଣ ସ୍ପର୍ଶକ :

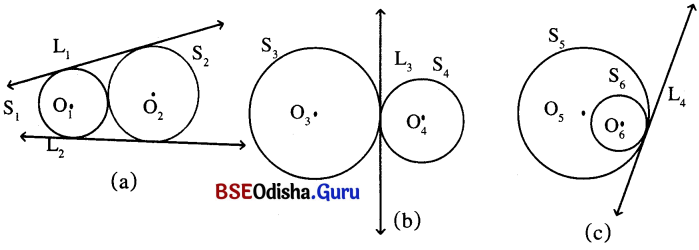
(i) ବହିଃସ୍ପର୍ଶୀ ସ୍ପର୍ଶକ ବୃତ୍ତର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ : ଚିତ୍ର (a)ରେ S₁ ଓ S₂ ବୃତ୍ତଦ୍ବୟ ସ୍ପର୍ଶକ ବୃତ୍ତ ( ବହିଃସ୍ପର୍ଶୀ) L₁ ଓ L₂ ଉଭୟ S₁ ଓ S₂ ବୃତ୍ତଦ୍ଵୟର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ।
(ii) ବହିଃସ୍ପର୍ଶୀ ସ୍ପର୍ଶକ ବୃତ୍ତର ତୀର୍ଯ୍ୟକ ସାଧାରଣ ସ୍ପର୍ଶକ : ଚିତ୍ର (b)ରେ S₃ ଓ S₄ ବହିଃସ୍ପର୍ଶୀ ସ୍ପର୍ଶକ ବୃତ୍ତ । L₃ ହେଉଛି ବୃତ୍ତଦ୍ଵୟର ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକ । ଏହା ବୃତ୍ତଦ୍ଵୟର ସ୍ପର୍ଶବିନ୍ଦୁରେ ହିଁ ବୃତ୍ତଦ୍ଵୟକୁ ସ୍ପର୍ଶ କରୁଛି ।
(iii) ଅନ୍ତଃସ୍ପର୍ଶୀ ସ୍ପର୍ଶକ ବୃତ୍ତର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ : ଚିତ୍ର (c)ରେ S₅ ଓ S₆ ବୃତ୍ତ ଦ୍ବୟ ଅନ୍ତଃସ୍ପର୍ଶୀ ସ୍ପର୍ଶକ ବୃତ୍ତ । L₄ ରେଖା ଉଭୟ ବୃତ୍ତର ସ୍ପର୍ଶ ବିନ୍ଦୁରେ ବୃତ୍ତଦ୍ଵୟକୁ ସ୍ପର୍ଶ କରୁଛି । ଏହା ହେଉଛି ବୃତ୍ତ ଦ୍ଵୟର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ।

(c) ପରସ୍ପରଛେଦୀ ଦୁଇଟି ଛେଦବିନ୍ଦୁ ଥ‌ିବା ବୃତ୍ତର ସାଧାରଣ ସ୍ପର୍ଶକ :

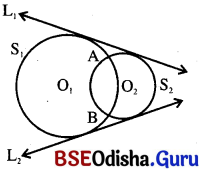
ଚିତ୍ରରେ S₁ ଓ S₂ ବୃତ୍ତଦ୍ଵୟ ପରସ୍ପରକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । ଏଠାରେ L₁ ଓ L₂ ରେଖାଦ୍ବୟ ପ୍ରତ୍ୟେକ S₁ ଓ S₂ ବୃତ୍ତଦ୍ଵୟକୁ ସ୍ପର୍ଶ କରନ୍ତି । ବୃତ୍ତଦ୍ଵୟର କେନ୍ଦ୍ର O₁ ଏବଂ O₂ ଉଭୟ L₁ ର ଗୋଟିଏ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ । O₁ ଏବଂ O₂ ଉଭୟ L₂ର ମଧ୍ୟ ଗୋଟିଏ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ । ଏଣୁ L₁ ଓ L₂ ପ୍ରତ୍ୟେକ, S₁ ଓ S₂ ବୃତ୍ତଦ୍ଵୟର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ।

ଉପପାଦ୍ୟ 15 :
ଦୁଇଟି ସ୍ପର୍ଶକ ବୃତ୍ତର କେନ୍ଦ୍ରଦ୍ଵୟ ଓ ସ୍ପର୍ଶବିନ୍ଦୁ ଏକ ସରଳରେଖାର ଅବସ୍ଥିତ ।
ଅନୁସିଦ୍ଧାନ୍ତ 1 : ଦୁଇଟି ବହିଃସ୍ପର୍ଶୀ ବୃତ୍ତର କେନ୍ଦ୍ରଦ୍ଵୟର ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା, ଉକ୍ତ ବୃତ୍ତଦ୍ବୟର ବ୍ୟାସାର୍ଦ୍ଧର ସମଷ୍ଟି ସହ ସମାନ ।
ଅନୁସିଦ୍ଧାନ୍ତ 2 : ଦୁଇଟି ଅନ୍ତଃସ୍ପର୍ଶୀ ବୃତ୍ତର କେନ୍ଦ୍ରତ୍ୱୟର ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା ଉକ୍ତ ବୃତ୍ତଦ୍ଵୟର ବ୍ୟାସାର୍ଦ୍ଧର ଅନ୍ତର ସହ ସମାନ ।