BSE Odisha 10th Class Maths Solutions Algebra Chapter 3 ସମାନ୍ତର ପ୍ରଗତି Ex 3(a)

Odisha State Board BSE Odisha 10th Class Maths Solutions Chapter 3 ସମାନ୍ତର ପ୍ରଗତି Ex 3(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Algebra Chapter 3 ସମାନ୍ତର ପ୍ରଗତି Ex 3(a)

Question 1.
ନିମ୍ନଲିଖତ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ସଠିକ୍ ଉତ୍ତରଟି ବାଛ ।
(i) 1, 2, 3, 4, …….. ଅନୁକ୍ରମରେ t₈ = …………..
(a) 6
(b) 7
(c) 8
(d) 9
ଉ-
(c) 8

(ii) 2, 4, 6, 8, …….. ଅନୁକ୍ରମରେ t₇ = …………..
(a) 12
(b) 14
(c) 16
(d) 18
ଉ-
(b) 14

(iii) – 5, – 3, – 1, 1, ……. ଅନୁକ୍ରମରେ t₁₁ = …………..
(a) 13
(b) 15
(c) 17
(d) 19
ଉ-
(b) 15

(iv) 3, 6, 9, ……… ରେ ସାଧାରଣ ଅନ୍ତର d = …………..
(a) 3
(b) 4
(c) 5
(d) 6
ଉ-
(a) 3

(v) -4, -2, 0, 2, A.P. ରେ ସାଧାରଣ ଅନ୍ତର d = …………..
(a) – 2
(b) -3
(c) 2
(d) 3
ଉ-
(c) 2

(vi) 10.2, 10.4, 10.6, 10.8, …. ରେ ସାଧାରଣ ଅନ୍ତର t₅ = …………..
(a) 11.0
(b) 11.2
(c) 11.4
(d) 11.6
ଉ-
(a) 11.0

(vii) 2.5, 2.9, 3.3, 3.7, ….. A.P. ରେ ସାଧାରଣ ଅନ୍ତର d = …………..
(a) 1.5
(b) 1.4
(c) 0.5
(d) 0.4
ଉ-
(d) 0.4

(viii) 3, x, 9, ଏକ A.P. ହେଲେ x = …………
(a) 4
(b) 5
(c) 6
(d) 7
ଉ-
(c) 6

(ix) 1.01, 1.51, 2.01, 2.51, ……. A.P. ରେ ସାଧାରଣ ଅନ୍ତର d = …………..
(a) 1
(b) 0.5
(c) 1.5
(d) 1.05
ଉ-
(b) 0.5

(x) 5, 0, -5, 10, ………. A.P. ରେ ସାଧାରଣ ଅନ୍ତର d = …………..
(a) – 5
(b) 5
(c) – 10
(d) 10
ଉ-
(a) – 5

ବ୍ୟାଖ୍ୟା ସହ ଉତ୍ତର:
(i) 1, 2, 3, 4, …….. ଅନୁକ୍ରମର t₈ = 8
(କାରଣ ଏଠାରେ t₁ = 1, t₂ = 2, t₃ = 3, t₈ = 8)

(ii) 2, 4, 6, 8 ……. ଅନୁକ୍ରମର t = 14
(କାରଣ t₁ = 2 × 1, t₂ = 2 × 2, t₃ = 2 × 3, t₇ = 2 × 7 = 14)

(iii) -5, -3, – 1, 1 ଅନୁକ୍ରମର t₁₁ = 15
(t₁₁ = 5 + (11 – 1) 2 = -5 + 20= 15).

(iv) 3,6,9, 60 ରେ ସାଧାରଣ ଅନ୍ତର d = 3
(କାରଣ 6 – 3 = 9 – 6 = 3)

(v) -4, -2, 0, 2 ……. A.P. ରେ ସାଧାରଣ ଅନ୍ତର d = 2
(କାରଣ -2 – (-4) = 0 -(-2) = 2)

(vi) 10.2, 10.4, 10.6, 10.8…… ରେ t₂ = 11
(କାରଣ 10.2 + (5 – 1) × 0.2 = 10.2 + 0.8 = 11)

(vii) 2.5, 2.9, 3.3, 3.7 …….. A.P. ରେ ସାଧାରଣ ଅନ୍ତର d = 0.4
(କାରଣ 2.9 – 2.5 = 3.3 – 2.9 = 0.4)

(viii) 3, x, 9 ….. A.P. ହେଲେ x = 6
(କାରଣ x = \(\frac{3+9}{2}\) = \(\frac{12}{2}\) =6)

(ix) 1.01, 1.51, 2.01, 2.51, ……. A.P. ରେ ସାଧାରଣ ଅନ୍ତର d = …………..
(କାରଣ 1.51 – 1.01 = 2.01 – 1.51 = 0.50)

(x) 5, 0, -5, 10, ………. A.P. ରେ ସାଧାରଣ ଅନ୍ତର d = …………..
(କାରଣ 0 – 5 = -5 – 0 = -5)

Question 2.
ନିମ୍ନଲିଖୂତ ଅନୁକ୍ରମ ମଧ୍ୟରୁ କେଉଁଗୁଡ଼ିକ A.P, ସେଗୁଡ଼ିକୁ ଚିହ୍ନଟ କର :
(i) 1, 4, 7, 10, 15, 16, 19, 22
(ii) 1, 8, 15, 22, 29, 36, 43, 50
(iii) 1, 6, 11, 15, 22, 28, 34, 40
(iv) 1, 4, 7, 9, 11, 14, 17, 20
(v) – 5, -3, -1, 0, 2, 4, 6, 8
(vi) a, a + d, a + 2d, a + 3d, a + 4d, a + 5d, a + 6d, a + 7d
(vii) 0.6, 0.8, 1.0, 1.5, 1.7, 1.8, 1.9, 2.0
(viii) -7,-4,- 1, 2, 5, 8, 11, 14
ଉ –
ନିମ୍ନଲିଖୂତ ଅନୁକ୍ରମ ମଧ୍ୟରୁ (ii), (vi) ଏବଂ (viii) ଗୁଡ଼ିକ A.P. ଅଟନ୍ତି ।

ବ୍ୟାଖ୍ୟା ସହ ଉତ୍ତର:
(i) 1, 4, 7, 10, 15, 16, 19, 22 ଅନୁକ୍ରମଟି A.P. ନୁହେଁ ।
(କାରଣ 4 – 1 ≠ 16 – 15, ଏଠାରେ ଯେକୌଣସି ପଦରୁ ତା’ର ପୂର୍ବ ପଦକୁ ବିୟୋଗ କଲେ ବିୟୋଗଫଳ ସମାନ ରହୁନାହିଁ ।)

(ii) 1, 8, 15, 22, 29, 36, 43, 50 ଅନୁକ୍ରମଟି A.P. ଅଟେ ।
(କାରଣ ଏଠାରେ ସାଧାରଣ ଅନ୍ତର (d) = 7 ଅଟେ ।)

(iii) 1, 6, 11, 15, 22, 28, 34, 40 ଅନୁକ୍ରମଟି A.P. ନୁହେଁ ।
(କାରଣ 6 – 1 ≠ 15 – 11, ଏଠାରେ d ସମାନ ନୁହେଁ ।)

(iv) 1, 4, 7, 9, 11, 14, 17, 20 ଅନୁକ୍ରମଟି A.P. ନୁହେଁ ।
(କାରଣ 4 – 1 ≠ 11 – ୨ ଏଠାରେ d ସମାନ ନୁହେଁ ।)

(v) -5, -3, -1, 0, 2, 4, 6, 8 ଅନୁକ୍ରମଟି A.P. ନୁହେଁ ।
(କାରଣ – 3 – (- 5) = 2 କିନ୍ତୁ 0 – (- 1) = 1, ଏଠାରେ d ସମାନ ନୁହେଁ ।)

(vi) a, a + d, a + 2d, a + 3d, a + 4d, a + 5d, a + 6d, a + 7d ଅନୁକ୍ରମଟି A.P. ଅଟେ ।
ଅନୁକ୍ରମର t₁ = a ଏବଂ ସାଧାରଣ ଅନ୍ତର = d)

(vii) 0.6, 0.8, 1.0, 1.5, 1.7, 1.8, 1.9, 2.0 ଅନୁକ୍ରମଟି A.P. ନୁହେଁ ।
(କାରଣ d ସବୁ କ୍ଷେତ୍ରରେ ସମାନ ନୁହେଁ ।)

(viii) -7,-4,-1, 2, 5, 8, 11, 14 ଅନୁକ୍ରମଟି A.P. ନୁହେଁ ।
(କାରଣ d = -4 – (-7) = -1 – (-4) = 2 – (-1) = 8 – 5 = 11 – 8 = 14 – 11 = 3)

Question 3.
ପ୍ରଶ୍ନ 2ରେ ଯେଉଁଗୁଡ଼ିକ A.P. ସେମାନଙ୍କ କ୍ଷେତ୍ରରେ ସାଧାରଣ ଅନ୍ତର ନିରୂପଣ କର ।
ସମାଧାନ :
(ii) 1, 8, 15, 22, 29, 36, 43, 50 ଅନୁକ୍ରମଟି A.P. ଅଟେ ।
ଏହି ଅନୁକ୍ରମର ସାଧାରଣ ଅନ୍ତର (d) = 8 – 1 = 15 – 8 = 7

(vi) , a + d, a + 2d, a + 3d, a + 4d, a + 5d, a + 6d, a + 7d ଅନୁକ୍ରମଟି A.P. ଅଟେ ।
ଏଠାରେ ସାଧାରଣ ଅନ୍ତର (d) = a + 4d – a – 3d = d

(viii) -7,-4,-1, 2, 5, 8, 11, 14 ଅନୁକ୍ରମଟି A.P. ଅଟେ ।
ଅନୁକ୍ରମଟିର ସାଧାରଣ ଅନ୍ତର (d) = – 4 – (- 7) = 3

Question 4.
ପ୍ରଥମ ପଦ a = 5 ନେଇ A.P.ର ପ୍ରଥମ ଚାରିଗୋଟି ପଦ ଲେଖ ଯେପରିକି ସାଧାରଣ ଅନ୍ତର
(i) d = 5
(ii) d = 4
(iii) d = 2
(iv) d =-2
(v) d=-3 ହେବ |
ସମାଧାନ :
(i) ପ୍ରଥମ ପଦ a = 5, d = 5 ହେଲେ,
t₁ = a = 5, t₂ = a + d = 5 + 5 = 10, t₃ = a + 2d = 5 + 2 × 5 = 15
t₄ = a + 3d = 5 + 3 × 5 = 20
∴ A.P.ର ପ୍ରଥମ ଚାରିଗୋଟି ପଦ 5, 10, 15 ଓ 20 1

(ii) a = 5, d = 4 ହେଲେ,
t₁ = a = 5, t₂ = a + d = 5 + 4 = 9, t₃ = a + 2d = 5 + 2 × 4 = 13
t₄ = a + 3d = 5 + 3×4 = 17
∴ A.P.ର ପ୍ରଥମ ଚାରିଗୋଟି ପଦ 5, 9, 13 ଓ 17 !

(iii) a = 5, d = 2 ହେଲେ,
t₁ = a = 5, t₂ = a + d = 5 + 2 = 7, t₃ = a + 2d = 5 + 2 × 2=9
t₄ = a + 3d = 5 + 3 × 2 = 11
∴ A.P.ର ପ୍ରଥମ ଚାରିଗୋଟି ପଦ 5, 7, 9 ଓ 11 1

(iv) a = 5, d= – 2 ହେଲେ,
t₁ = a = 5, t₂ = a + d = 5 + (- 2) = 3, t₃ = a + 2d = 5 + 2 (- 2) = 1
t₄ = a + 3d = 5 + 3 (- 2) = – 1
∴ A.P.ର ପ୍ରଥମ ଚାରିଗୋଟି ପଦ 5, 2, – 1 ଓ – 4 ।

(v) a = 5, d = -3 ହେଲେ,
t₁ = a = 5, t₂ = a + d = 5 + (- 3) = 2, t₃ = a + 2d = 5 + 2 (- 3) = – 1
t₄ = a + 3d = 5 + 3 (- 3) = – 4
∴ A.P.ର ପ୍ରଥମ ଚାରିଗୋଟି ପଦ 5, 2, – 1 ଓ – 4 ।

Question 5.
ଏକ A.P.ର n ତମ ପଦ । ନିମ୍ନରେ ପ୍ରଦତ୍ତ ହୋଇଛି । ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ t₅, t₈ ଓ t₁₀ କେତେ ନିରୂପଣ କର।
(i) t_n = \(\frac{n+1}{2}\)
(ii) t_n = -10 + 2n
(iii) t_n = 10n + 5
(iv) t_n = 4n – 6
ସମାଧାନ :
(i) ଏକ A.P. ର t_n = \(\frac{n+1}{2}\)
t₅ = \(\frac{6+1}{2}=\frac{6}{2}=3\)

t₈ = \(\frac{8+1}{2}=\frac{9}{2}=4.5\)

t₁₀ = \(\frac{10+1}{2}=\frac{11}{2}=5.5\)

(ii) t_n = -10 + 2n
t₅ = -10 +2 × 5
= – 10 + 10 = 0,

t₈ = -10 + 2 × 8
= -10 + 16 = 6

t₁₀ = -10 + 2 × 10
= 10 + 20= 10

(iii) t_n = 10n + 5
t₅ = 10 × 5 + 5 = 55,
t₈ = 10 × 8+ 5 = 85,
t₁₀ = 10 x 10 + 5 = 105

(iv) t_n = 4n – 6,
t₅ = 4 × 5 – 6
= 20 – 6 = 14

t₈ = 4 × 8 – 6
= 32 – 6 = 26

t₁₀ = 4 × 10 – 6
= 40 – 6 = 34

Question 6.
ନିମ୍ନଲିଖୂ A.P. ଗଠନ କର (କେବଳ ଦ୍ବିତୀୟ, ତୃତୀୟ ଓ ଚତୁର୍ଥ ପଦ ତ୍ରୟ ଆବଶ୍ୟକ) ଯେଉଁଠାରେ :
(i) ପ୍ରଥମ ପଦ a = 4, ସାଧାରଣ ଅନ୍ତର d =3
(ii) ପ୍ରଥମ ପଦ a = -8, ସାଧାରଣ ଅନ୍ତର d = – 2
(iii) ପ୍ରଥମ ପଦ a = 7, ସାଧାରଣ ଅନ୍ତର d = – 4
(iv) ପ୍ରଥମ ପଦ a = 10, ସାଧାରଣ ଅନ୍ତର d = 5
(v) ପ୍ରଥମ ପଦ a = \(\frac{1}{2}\), ସାଧାରଣ ଅନ୍ତର d = \(\frac{3}{2}\)
(vi) ପ୍ରଥମ ପଦ a = \(\frac{1}{2}\), ସାଧାରଣ ଅନ୍ତର d = -1
ସମାଧାନ :
(i) ଏକ A.P.ର ପ୍ରଥମ ପଦ a = 4, ସାଧାରଣ ଅନ୍ତର d = 3
t₂ = a + d = 4 + 3 = 7,
t₃ = a + 2d = 4 + 2 × 3 = 10
t₄= a + 3d = 4 + 3 × 3 = 13

(ii) a = -8, d = -2
t₂ = a + d = -8 + (- 2) = – 10
t₃ = a + 2d = – 8 + 2 × (- 2) = – 8 – 4 = – 12
t₄ = a + 3d = -8 + 3 (- 2) = – 8 – 6=-14

(iii) a = 7, d=-4
t₂ = a + d = 7+ (- 4) = 3,
t₃ = a + 2d = 7 + 2 (- 4) = 7 – 8 = -1
t₄ = a + 3d = 7+ 3 (- 4) = 7 – 12 = – 5

(iv) a = 10, d = 5
t₂ = a + d = 10 + 5 = 15,
t₃ = a + 2d = 10 + 2 × 5 = 20
t₄ = a + 3d = 10 + 3 × 5 = 10 + 15 = 25

(v) a = \(\frac{1}{2}\), d = \(\frac{3}{2}\)
t₂ = a + d = \(\frac{1}{2}+\frac{3}{2}=\frac{4}{2}=2\)
t₃ = a + 2d = \(\frac{1}{2}+2 × \frac{3}{2}=\frac{1}{2}+3=\frac{7}{2}\)
t₄ = a + 3d = \(\frac{1}{2}+3 × \frac{3}{2}=\frac{1}{2}+\frac{9}{2}=\frac{10}{2}=5\)

(vi) a = \(\frac{1}{2}\), d = -1
t₂ = a + d = \(\frac{1}{2}-1=-\frac{1}{2}\)
t₃ = a + 2d = \(\frac{1}{2}+2(-1)=\frac{1}{2}-2=\frac{1-4}{2}=\frac{-3}{2}\)
t₄ = a + 3d = \(\frac{1}{2}+3(-1)=\frac{1}{2}-3=\frac{1-6}{2}=\frac{-5}{2}\)

Question 7.
ନିମ୍ନରେ ପ୍ରଦତ୍ତ ଉକ୍ତିଗୁଡ଼ିକ ଭୁଲ୍ ବା ଠିକ୍ ଲେଖ ।
(a) 1, 2, 3, 4 ……. ସମାନ୍ତର ପ୍ରଗତି ସୃଷ୍ଟି କରନ୍ତି ।
(b) 1, – 1, 1, -1, -1, ……. ଅନୁକ୍ରମଟି ସମାନ୍ତର ପ୍ରଗତି ଅଟେ ।
(c) 2, 1, – 1, – 2 ସଂଖ୍ୟା ଚାରିଗୋଟି ସମାନ୍ତର ପ୍ରଗତିରେ ବିଦ୍ୟମାନ ।
(d) ଯେଉଁ ଅନୁକ୍ରମର t = n – 1, ତାହା ଏକ A.P. ଅଟେ ।
(e) ଯେଉଁ ଅନୁକ୍ରମର S_n = \(\frac{n(n-1)}{2}\) ତାହା A.P. ଅଟେ ।
(f) ଯଦି କୌଣସି ତ୍ରିଭୁଜର କୋଣ ତ୍ରୟର ପରିମାଣର ଅନୁପାତ 2 : 3 : 4 ହୁଏ, ତେବେ କୋଣତ୍ରୟର ପରିମାଣ ଗୋଟିଏ A.P. ଗଠନ କରିବେ ।
(g) ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ ଗୋଟିଏ A.P.ରେ ରହିପାରିବେ ।
(h) ଅଯୁଗ୍ମ ସଂଖ୍ୟାମାନେ A.P. ଗଠନ କରନ୍ତି ନାହିଁ ।
(i) 5 ଦ୍ବାରା ବିଭାଜ୍ୟ ସମସ୍ତ ଗଣନ ସଂଖ୍ୟା ଏକ A.P. ଅଟନ୍ତି ।
(j)5, x, ୨ ସଂଖ୍ୟାତ୍ରୟ ସମାନ୍ତର ପ୍ରଗତିରେ ରହିଲେ x = 6 I
ଉ –
(a) ଠିକ୍, (b) ଭୁଲ୍, (c) ଭୁଲ୍, (d) ଠିକ୍, (e) ଠିକ୍, (f) ଭୁଲ୍, (g) ଭୁଲ୍, (h) ଭୁଲ୍, (i) ଠିକ୍, (j) ଭୁଲ

ବ୍ୟାଖ୍ୟା ସହ ଉତ୍ତର :
(a) 1, 2, 3, 4 ………. ସମାନ୍ତର ପ୍ରଗତି ସୃଷ୍ଟି କରନ୍ତି । (ଠିକ୍)
(କାରଣ ଏହି ଅନୁକ୍ରମର ସାଧାରଣ ଅନ୍ତର (d) = 1)
(b) 1, – 1, 1, – 1, ……. ଅନୁକ୍ରମଟି ସମାନ୍ତର ପ୍ରଗତି ଅଟେ । (ଭୁଲ୍)
(କାରଣ ଏହି ଅନୁକ୍ରମର ଓଁ ସମାନ ନୁହେଁ ।)
(c) 2, 1, – 1, – 2 ସଂଖ୍ୟାଟି ଚାରିଗୋଟି ସମାନ୍ତର ପ୍ରଗତିରେ ବିଦ୍ୟମାନ । (ଭୁଲ୍)
(କାରଣ 1 – 2 = -1, -1 – 1 = -2 ଏଠାରେ d ଅସମୀନ)
(d) t = n – 1 ଏକ A.P. ଅଟେ । (ଠିକ୍)
(କାରଣ ଅନୁକ୍ରମର ସାଧାରଣ ପଦ t_n = n – 1)
(e) ଯେଉଁ ଅନୁକ୍ରମର S_n = \(\frac{n(n-1)}{2}\) ତାହା A.P. ଅଟେ । (ଠିକ୍)
(f) ଯଦି କୌଣସି ତ୍ରିଭୁଜର କୋଣ ତ୍ରୟର ପରିମାଣର ଅନୁପାତ 2 : 3 : 4 ହୁଏ, ତେବେ କୋଣତ୍ରୟର ପରିମାଣ ଗୋଟିଏ A.P. ଗଠନ କରିବେ । (ଠିକ୍)
(କାରଣ କୋଣତ୍ରୟ 40°, 60°, 80° ଏହା A.P. ଅଟେ ।)
(g) ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ ଗୋଟିଏ A.P.ରେ ରହିପାରିବେ । (ଭୁଲ୍)
(କାରଣ 3, 4, 5; 6, 8, 10 ଇତ୍ୟାଦି ସମକୋଣୀ ତ୍ରିଭୁଜର ବାହୁ; କିନ୍ତୁ ଯେକୌଣସି ସମକୋଣୀ ତ୍ରିଭୁଜ ପାଇଁ ଠିକ୍ ନୁହେଁ ।)
(h) ଅଯୁଗ୍ମ ସଂଖ୍ୟାମାନେ A.P. ଗଠନ କରନ୍ତି ନାହିଁ । (ଭୁଲ୍)
(3, 5, 7, 9 A.P. ଗଠନ କରନ୍ତି ।)
(i) 5 ଦ୍ବାରା ବିଭାଜ୍ୟ ସମସ୍ତ ଗଣନ ସଂଖ୍ୟା ଏକ A.P. ଅଟନ୍ତି । (ଠିକ୍)
(କାରଣ 5, 10, 15, 20 A.P. ଅଟନ୍ତି ।)
(j) 5, x, ୨ A.P. ରେ ରହିଲେ x = 6 । (ଭୁଲ୍) ( କାରଣ x = \(\frac{9+5}{2}=\frac{14}{2}=7\)

‘ଖ’ ବିଭାଗ

Question 8.
(a) 1 + 2 + 3 + ….. ରେ S₃₀ କେତେ ?
(b) 1 + 3 + 5 + …….. ରେ S₁₀ କେତେ ?
(c) 2 + 4 + 6 + …….ରେ S₁₅ କେତେ ?
(d) 1 – 2 + 3 – 4 + ….. ରେ S₃₀ କେତେ ?
(e) 1 – 2 + 3 – 4 + …….. ରେ S₄₁ କେତେ ?
(f) 1 + 1 + 2 + 2 + 3 + 3 ……… ରେ S₁₇ କେତେ ?
(g) 1 + 2 + 3 + 2 + 3 + 4 + 3 + 4 + 5 ….. ରେ S₃₉ କେତେ ?
(h) -7 – 10 – 13 – ……… ରେ S₂₁ କେତେ ?
(i) 10 + 6 + 2 + ……. ରେ S₁₅ କେତେ ?
(j) 20 + 9 – 2 + …….. ରେ S₂₅ କେତେ ?
(k) n + (n – 1) + (n – 2) + ……… ରେ S_n କେତେ ?
(l) \(5+4 \frac{1}{3}+3 \frac{2}{3}\) + ……… ରେ S₂₀ କେତେ ?
ସମାଧାନ :
(a) S_n = \(\frac{n}{2}\) {2a + (n – 1) d}
ଏଠାରେ a = 1, d= 3 – 2 = 2 – 1 = 18 ଓ n = 30
S_n = \(\frac{n}{2}\) {2a + (n – 1) d}
S₃₀ = \(\frac{30}{2}\) {2.1 + (30 – 1) .1} = 15(2 + 29) = 15 × 31 = 465

(b) ଏଠାରେ a = 1, d= 3 – 1 = 5 – 3 = 2, n = 10
S_n = \(\frac{n}{2}\) {2a + (n – 1) d}
⇒ S₁₀ = \(\frac{10}{2}\) {2.1 + (10 – 1) 2} = 15(2 + 29) = 5 × 20 = 100

(c) ଏଠାରେ a = 2, d= 4 – 2 = 6 – 4 = 2, n = 15
S₁₅ = \(\frac{15}{2}\) {2 × 2 + (15 – 1) 2} = \(\frac{15}{2}\)(4 + 28) = 15 × 16 = 240

(d) 1 – 2 + 3 – 4 + ……… S₃₀
ଦତ୍ତ ଅନୁକ୍ରମଟି A.P.ରେ ନାହିଁ ।
ଦୁଇଟି ପଦକୁ ଗୋଟିଏ ପଦରେ ପରିଣତ କଲେ ଏହା ଅନୁକ୍ରମ ହେବ ଓଏହା S₁₅ ହେବ ।
= (1 – 2) + (3 – 4) + (5 – 6) + ……… (29 – 30)
= (- 1) + (- 1) + (- 1) + ………. = -1 × 15 = -15

(e) 1 – 2 + 3 – 4 + ……… ରେ S₄₁
ପଦସଂଖା 41 ହେତୁ ଅନୁକ୍ରମଟି
(1 – 2) + (3 – 4) + ……. (39 – 40) + 41
= ( – 1 ) + ( – 1) + (- 1) + ……. S₂₀ + 41 = -20 + 41 = 21

(f) 1 + 1 + 2 + 2 + 3 + 3 ……… ରେ S₁₇ ନିର୍ଣ୍ଣୟ କରାଯିବ ।
= (1 + 2 + 3 + ……. + 9) + (1 + 2 + 3 + ……. + 8)
= \(\frac{9×10}{2}+\frac{8×9}{2}\) (∵ Sn = \(\frac{n(n-1)}{2}\))
= 9 × 5 + 4 × 9 = 45 + 36 = 81

(g) 1 + 2 + 3 + 2 + 3 + 4 + 3 + 4 + 5 ….. ରେ S₃₉ କେତେ ?
ତିନୋଟି ପଦକୁ ଗୋଟିଏ ପଦରେ ପରିଣତ କଲେ, 39ଟି ପଦ \(\frac{39}{3}\) = 13ଟି ପଦ ହେବ ।
(1 + 2 + 3) + (2 + 3 + 4) + (3 + 4 +5) ………. ରେ S₁₃
6 + 9 + 12 + ……. ରେ S₁₃
= \(\frac{13}{2}\) {2 × 6 + (13 – 1) 3} = \(\frac{13}{2}\) {12 + 36} = \(\frac{13}{2}\) × 48 = 13 × 24 = 312

(h) S_n = \(\frac{n}{2}\) {2a + (n – 1) d}
ଏଠାରେ a = – 7, d = -10 – (-7) = – 10 + 7 = – 3, n = 21
S₂₁ = \(\frac{21}{2}\) {2 · (- 7) + (21 – 1) (- 3)}
= \(\frac{21}{2}\) { – 14 – 60} = = \(\frac{21}{2}\) { -74) = 21 × (-37) =-777

(i) ଏଠାରେ a = 10, d = 6 – 10 = 2 – 6 = – 4, n = 15
S₁₅ = \(\frac{15}{2}\) {2 × 10 + (15 – 1) (- 4)}
= \(\frac{15}{2}\) {20+ (-56)} = \(\frac{15}{2}\) × -36 = 15 × (-18) = -270

(j) S_n = \(\frac{n}{2}\) {2a + (n – 1) d}
ଏଠାରେ a = 20, d = 9 – 20 = -2 – 9 = – 11, n = 25
S₂₅ = \(\frac{25}{2}\) {2 × 20+ (25 – 1) (- 11)}
= \(\frac{25}{2}\) {40 + 24 × (-11)} = \(\frac{25}{2}\) (40 – 264)
= \(\frac{25}{2}\) × – 224 = 25 × (- 112) = – 2800

(k) ଏଠାରେ a = n, d = (n – 1) – n = -1, n = n
S_n = \(\frac{n}{2}\) {2a + (n – 1) d} = \(\frac{n}{2}\) {2n + (n – 1)(-1)}
=\(\frac{n}{2}\) (2n – n + 1) = \(\frac{n}{2}\) (n + 1)

(l) ଏଠାରେ a = 5, d = \(4 \frac{1}{3}-5=\frac{13}{3}-5=\frac{13-15}{3}=-\frac{2}{3}\), n = 20
S₂₀ = \(\frac{20}{2}\) {2 × 5 + (20 – 1) (-3)} [∵ S_n = \(\frac{n}{2}\) {2a + (n – 1) d}]
= 10 {10 – \(\frac{38}{3}\)} = 10 (\(\frac{30-38}{3}\)) = 10 × \(\frac{-8}{3}\) = \(\frac{-80}{3}\) = \(-26 \frac{2}{3}\)

Question 9.
(a) ଯଦି a = 3, d = 4, n = 10, ତେବେ S_n କେତେ ?
(b) ଯଦି a = – 5, d = – 3, ତେବେ S₁₇ କେତେ ?
(c) ଯଦି t_n = 2n – 1, ତେବେ ପ୍ରଥମ 5ଟି ପଦ ଲେଖ ।
(d) ଯଦି t_n = 3n + 2, S₆₁ ନିର୍ଣ୍ଣୟ କର ।
(e) ଯଦି t_n = 3n – 5, ତେବେ S₅₀ ନିର୍ଣ୍ଣୟ କର ।
(f) ଯଦି t_n = 2 – 3n, ତେବେ S_n ନିର୍ଣ୍ଣୟ କର ।
(g) ଯଦି S_n = n², ତେବେ t₁₅ କେତେ ?
(h) ଏକ A.P.ର a = 3, d = 4, S_n = 903, ତେବେ n କେତେ?
(i) ଏକ A.P. ର d = 2, S₁₅ = 285, ତେବେ a କେତେ?
(j) ଏକ A.P. ର t₁₅ = 30, t₂₀ = 50, ତେବେ S₁₇ କେତେ?
ସମାଧାନ :
MBD
(a) S_n = \(\frac{n}{2}\) {2a + (n – 1) d}
ଏଠାରେ a = 5, d = 4, n = 10
S₁₀ = \(\frac{10}{2}\) {2 × 3 + (10 – 1) 4} = 5 {6 + 36} = 5 × 42 = 210

(b) S_n = \(\frac{n}{2}\) {2a + (n – 1) d}
ଏଠାରେ a = -5, d = -3, n = 17
S₁₇ = \(\frac{17}{2}\) {2 × (-5) + (17 – 1) (-3)} = \(\frac{17}{2}\) {-10 – 48} = \(\frac{17}{2}\) × (-58) = 17 × (-29) = – 493

(c) t_n = 2n – 1,
t₁ = a = 2 × 1 – 1 = 2 – 1 = 1
t₂ = a = 2 × 2 – 1 = 4 – 1 = 3,
t₃ = a = 2 × 3 – 1 = 6 – 1 = 5,
t₄ = a = 2 × 4 – 1 = 8 – 1 = 7,
t₅ = a = 2 × 5 – 1 = 10 – 1 = 9,

(d) t_n = 3n + 2
t₁ = a = 3 × 1 + 2 = 5
t₂ = a = 3 × 2 + 2 = 8
t₃ = a = 3 × 3 + 2 = 11
ଏଠାରେ a = 5, d = 8 – 5 = 11 – 8 = 3, n = 61
S_n = \(\frac{n}{2}\) {2a + (n – 1) d}
S₆₁ = \(\frac{61}{2}\) {2 × 5+ (61 – 1) 3} = \(\frac{61}{2}\) {10 + 180} = 61 × 95 = 5795

(e) t_n = 3n – 5
t₁ = 3 × 1 – 5 = -2
t₂ = 3 × 2 – 5 = 1
t₂ = 3 × 3 – 5 = 4
a = -2, d = 1 – (- 2) = 4 – 1 = 3, n = 50
S₅₀ = \(\frac{50}{2}\) {2 × (-2) + (50 – 1) 3} = 25 × (- 4 + 147) = 25 × 143 = 3575

(f) t_n = 2 – 3n
t₁ = 2 – 3 × 1 = – 1
t₂ = 2 – 3 × 2 = -4
t₃ = 2 – 3 × 3 = -7 ଇତ୍ୟାଦି
ଏଠାରେ a = -1, d= – 4 – (- 1) = -7 – (- 4) = -3
S_n = \(\frac{n}{2}\) {2a + (n – 1) d} = \(\frac{n}{2}\) (2 × (- 1) + (n – 1) (- 3)}
= \(\frac{n}{2}\) (-2 – 3n + 3} = \(\frac{n}{2}\) (1 – 3n)

(g) t_n = S_n – S_n-1
S_n = n², S₁₅ = 15², S₁₄ = 14²
t₁₅ = S₁₅ – S₁₄ = 15² – 14² = 225 – 196 = 29

(h) ଏକ A.P.ର a = 3, d = 4, S_n = 903

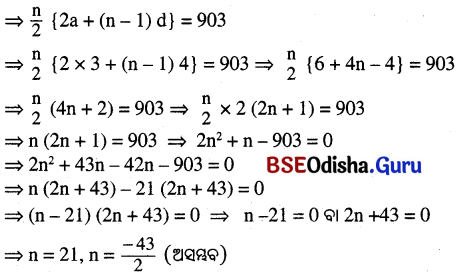
∴ n = 2

(i) A.P.ର d = 2, S₁₅ = 285, n = 15

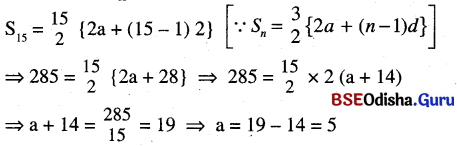
(j) ମନେକର A.P.ର ପ୍ରଥମ ପଦ = a ଓ ସାଧାରଣ ଅନ୍ତର = d
t₁₅ = 30 ⇒ a + (15 – 1) d = 30 ⇒ a + 14d = 30 …(i)
t₂₀ = 50 ⇒ a + (20 – 1) d = 50 ⇒ a + 19d = 50 …(ii)
ସମୀକରଣ (i)ରୁ (ii)କୁ ବିୟୋଗ କଲେ

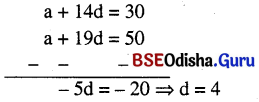
d ର ମାନ ସମୀକରଣ (i)ରେ ପ୍ରୟୋଗ କଲେ
a + 14d = 30 = a + 14 × 4 = 30
= a + 56 = 30 = a = 30 – 56 = -26
S₁₇ = \(\frac{17}{2}\) {-52 + (17 – 1)4} = \(\frac{17}{2}\) {-52 + 64}= \(\frac{17}{2}\) × 12 = 17 × 6 = 102

Question 10.
(i) ‘ଓଲଟାଇ ମିଶାଇବା କୌଶଳରେ’ ଯୋଗଫଳ ନିର୍ଣ୍ଣୟ କର ।
(a) 1 ଠାରୁ 105 ପର୍ଯ୍ୟନ୍ତ ସମସ୍ତ ଗଣନ ସଂଖ୍ୟା ।
(b) 25 ଠାରୁ 93 ପର୍ଯ୍ୟନ୍ତ ସମସ୍ତ ଗଣନ ସଂଖ୍ୟା ।
(c) 111 ଠାରୁ 222 ପର୍ଯ୍ୟନ୍ତ ସମସ୍ତ ଗଣନ ସଂଖ୍ୟା ।

(ii) 1, 2, 3, …….. ଅନୁକ୍ରମର।
(a) S₂₀ ନିଶ୍ଚୟ କର (b) S₅₀ ନିର୍ଣ୍ଣୟ କର ।
(iii) 32 ଠାରୁ 85 ପର୍ଯ୍ୟନ୍ତ ସମସ୍ତ ଗଣନ ସଂଖ୍ୟାର ସମଷ୍ଟି ନିର୍ଣ୍ଣୟ କର ।
(iv) 100 ଠାରୁ କ୍ଷୁଦ୍ରତର ସମସ୍ତ ଧନାତ୍ମକ ଯୁଗ୍ମ ସଂଖ୍ୟାର ସମଷ୍ଟି ନିର୍ଣ୍ଣୟ କର ।
(v) 150 ଠାରୁ କ୍ଷୁଦ୍ରତର ସମସ୍ତ ଧନାତ୍ମକ ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ସମଷ୍ଟି ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
(i) (a) 1 ଠାରୁ 105 ପର୍ଯ୍ୟନ୍ତ ଗଣନ ସଂଖ୍ୟାମାନଙ୍କର ମୋଟ ସଂଖ୍ୟା = 105
ମନେକର 1 ଠାରୁ 105 ପର୍ଯ୍ୟନ୍ତ ଗଣନ ସଂଖ୍ୟାମାନଙ୍କର ଯୋଗଫଳ = S

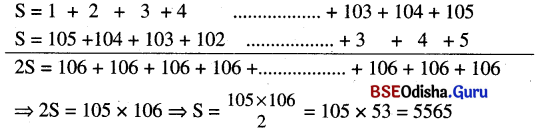
∴ 1 ଠାରୁ 105 ପର୍ଯ୍ୟନ୍ତ ଗଣନ ସଂଖ୍ୟାର ଯୋଗଫଳ = 5565

(b) 25 ଠାରୁ 93 ପର୍ଯ୍ୟନ୍ତ ଗଣନ ସଂଖ୍ୟାମାନଙ୍କର ମୋଟ ସଂଖ୍ୟା = 93 – 24 = 69
ମନେକର 25 ଠାରୁ 93 ପର୍ଯ୍ୟନ୍ତ ଗଣନ ସଂଖ୍ୟାମାନଙ୍କର ଯୋଗଫଳ = S

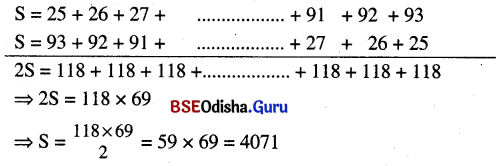
∴ 25 ଠାରୁ 93 ପର୍ଯ୍ୟନ୍ତ ଗଣନ ସଂଖ୍ୟାର ସମଷ୍ଟି = 4071

(c) 111 ଠାରୁ 222 ପର୍ଯ୍ୟନ୍ତ ଗଣନ ସଂଖ୍ୟାମାନଙ୍କର ସଂଖ୍ୟା = 222 – 110 = 112
ମନେକର 111 ଠାରୁ 222 ପର୍ଯ୍ୟନ୍ତ ଗଣନ ସଂଖ୍ୟାମାନଙ୍କର ଯୋଗଫଳ = S

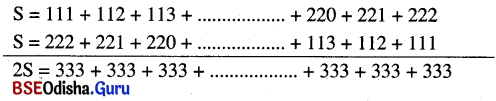
⇒ 2S = 333 × 112 ⇒ S = \(\frac{333×112}{2}\) = 333 × 56 = 18648
∴ ମନେକର 111 ଠାରୁ 222 ପର୍ଯ୍ୟନ୍ତ ଗଣନ ସଂଖ୍ୟାର ସମଷ୍ଟି = 18648

(ii) S_n = \(\frac{n(n-1)}{2}\)

(a) 1, 2, 3 ଅନୁକ୍ରମର S₂₀ = \(\frac{20×21}{2}\) = 10 × 21 = 210

(b) S₅₀ = \(\frac{50×51}{2}\) = 25 × 51 = 1275

(iii) S = 32 +33 +34 …….. + 85
ଏଠାରେ a = 32, d = 33 – 32 = 1, n = 85 – 31 = 54
S_n = \(\frac{n}{2}\) {2a + (n – 1) d} = \(\frac{54}{2}\) {2 × 32 + (54 – 1) × 1}
= 27 × {64 +53} = 27 × 117 = 3159
∴ ମନେକର 111 ଠାରୁ 222 ପର୍ଯ୍ୟନ୍ତ ଗଣନ ସଂଖ୍ୟାର ସମଷ୍ଟି 3159।

(iv) S_n = \(\frac{n(n-1)}{2}\)
100 ଠାରୁ କ୍ଷୁଦ୍ରତର ସମସ୍ତ ଧନାତ୍ମକ ଯୁଗ୍ମ ସଂଖ୍ୟାମାନଙ୍କର ସମଷ୍ଟି
S = 2 + 4 + 6 + 8 …… + 98
= 2 (1 + 2 + 3 + 4 ……. + 49)
= 2 × \(\frac{49 (49 + 1)}{2}\) = \(\frac{49×50}{2}\) = 49 × 50 = 2450
∴ 100 ଠାରୁ କ୍ଷୁଦ୍ରତର ସମସ୍ତ ଧନାତ୍ମକ ସଂଖ୍ୟାମାନଙ୍କର ସମଷ୍ଟି = 2450

(v) 150 ଠାରୁ କ୍ଷୁଦ୍ରତର ସମସ୍ତ ଅଯୁଗ୍ମ ସଂଖ୍ୟାମାନଙ୍କର ସମଷ୍ଟି
S = 1 + 3 + 5 + 7 ……. + 149
ଏଠାରେ a = 1, d = 3 – 1 = 5 – 3 = 2
t_n = 149
⇒ a + (n – 1) d = 149 ⇒ 1 + (n – 1) 2 = 149
⇒ n – 1 = \(\frac{149 – 1}{2}=\frac{148}{2}=74\) ⇒ n = 74 + 1 = 75
S_n = \(\frac{n}{2}\) {2a + (n – 1) d} = \(\frac{75}{2}\) {2 × 1 + (75 – 1) 2}
= \(\frac{75}{2}\) {2 + 148} = \(\frac{75×150}{2}\)
= 75 × 75 = 5625
∴ 150 ଠାରୁ କ୍ଷୁଦ୍ରତର ସମସ୍ତ ଧନାତ୍ମକ ଅଯୁଗ୍ମ ସଂଖ୍ୟାମାନଙ୍କର ସମଷ୍ଟି 5625 ।

Question 11.
ଯେଉଁ ସମାନ୍ତର ଅନୁକ୍ରମର ପ୍ରଥମ ପଦ 17 ଓ ସାଧାରଣ ଅନ୍ତର – 2 ତାହାର କେତୋଟି ପଦର ସମଷ୍ଟି 72 ହେବ ? ଏହାର ଦୁଇଟି ଉତ୍ତର ମିଳିବାର କାରଣ ଲେଖ ।
ସମାଧାନ :
ଏକ ଅନୁକ୍ରମର ପ୍ରଥମ ପଦ (a) = 17, ସାଧାରଣ ଅନ୍ତର (d) = – 2
ମନେକର nଟି ପଦର ସମଷ୍ଟି 72 ।
⇒ S_n = 72 ⇒ \(\frac{n}{2}\) {2a + (n – 1) d} = 72
⇒ \(\frac{n}{2}\) {2 × 17 + (n – 1) × (- 2)} = 72 ⇒ \(\frac{n}{2}\) {34 – 2n + 2} = 72
⇒ \(\frac{n}{2}\) {36 – 2n } = 72 ⇒ \(\frac{n}{2}\) × 2 (18 – 2n) = 72
⇒ 18n – 2n² – 72 = 0 ⇒ -2 (n² – 18n + 72) = 0
⇒ n² – 18n + 72 = 0 ⇒ n² – 12n – 6n + 72 = 0
⇒ n (n – 12) – 6 (n – 12) = 0 ⇒ (n – 6) (n – 12) = 0
n = 6 ବା n = 12
t₇ = a + (7 – 1) d = 17 + 6 (- 2) = 17 – 12 = 5
t₈ = a + (8 – 1) d = 17 + 7 (- 2) = 17 – 14 = 3
t₉ = a + (9 – 1) d = 17 + 8 (- 2) = 17 – 16 = 1
t₁₀ = a + (10 – 1) d = 17 + 9 (- 2) = 17 – 18 = – 1
t₁₁ = a + (11 – 1) d = 17 + 10 (- 2) = 17 – 20 = -3
t₁₂ = a + (12 – 1) d = 17 + 11 (- 2) = 17 – 22 = -5
∴ t₇ + t₁₁ ………. + t₁₂ = (5 + 3 + 1) – (1 + 3 + 5) = 0
∴ ସପ୍ତମ ପଦରୁ ଦ୍ଵାଦଶ ତମ ପଦ ପର୍ଯ୍ୟନ୍ତ ସଂଖ୍ୟାଗୁଡ଼ିକର ଯୋଗଫଳ 0 ହୋଇଥିବାରୁ
ପ୍ରଥମ 6ଟି ପଦର ସମଷ୍ଟି = ପ୍ରଥମ 12 ଟି ପଦର ସମଷ୍ଟି
ତେଣୁ ଆମେ ଦୁଇଟି ଉତ୍ତର ପାଇଲୁ ।

Question 12.
(i) ଏକ ସମାନ୍ତର ଅନୁକ୍ରମରେ ଅବସ୍ଥିତ ତିନୋଟି ରାଶିର ଯୋଗଫଳ 18 ଏବଂ ଗୁଣଫଳ 192 ହେଲେ, ସଂଖ୍ୟାଗୁଡ଼ିକ ସ୍ଥିର କର ।
(ii) ଏକ ସମାନ୍ତର ଅନୁକ୍ରମରେ ଅବସ୍ଥିତ ଛଅଟି ପଦ ମଧ୍ୟରୁ ପ୍ରାନ୍ତ ପଦଦ୍ୱୟର ଯୋଗଫଳ 16 ଏବଂ ମଧ୍ୟ ପଦଦ୍ୱୟର ଗୁଣଫଳ 63 ହେଲେ, ପଦଗୁଡ଼ିକ ସ୍ଥିର କର ।
ସମାଧାନ :
(i) ମନେକର ସମାନ୍ତର ଅନୁକ୍ରମର ଥ‌ିବା ପଦତ୍ରୟ a – d, a, a + d ।
ପ୍ରଶ୍ନନୁସାରେ ପଦତ୍ରୟର ଯୋଗଫଳ = 18
⇒ a – d + a + a + d = 18 ⇒ 3a = 18 ⇒ a = \(\frac{18}{3}\) ⇒ a = 6.
ପୁନଶ୍ଚ (a – d) × a (a + d) = 192 ⇒ a (a² – d²) = 192
⇒ 6 {(6)² – d²} = 192 ⇒ 36 – d² = \(\frac{192}{6}\) = 32
⇒ d² = 32 – 36 = -4 ⇒ d² = 4 ⇒ d= ±√4⇒ d = ±2
a = 6 ଓ d = 2 ହେଲେ A.P. ର ପଦତ୍ରୟ a – d = 6 – 2 = 4
a = 6 ଏବଂ a + d = 6 + 2 = 8
a = 6 ଓ d = – 2 ହେଲେ A.P.ର ପଦତ୍ରୟ a – d = 6 – (-2) = 6 + 2 = 8
a = 6, a – d = 6 + (- 2) = 6 – 2 = 4
∴ A.P.ର ପଦତ୍ରୟ 4, 6, 8 ବା 8, 6, 4 ।

(ii) ମନେକର ସମାନ୍ତର ଅନୁକ୍ରମର ଥ‌ିବା ଛଅଟି ପଦ a – 5d, a – 3d, a – d, a + d, a + 3d, a + 5d ।
ପ୍ରଶ୍ନନୁସାରେ, a – 5d + a + 5d = 16 ⇒ a = \(\frac{16}{2}\) = 8
ପୁନଶ୍ଚ (a – d) × (a + d) = 63
⇒ (a² – d²) = 63 ⇒ 64 – d² = 63
⇒ d² = 1 ⇒ d = ± √1 = ±1
a = 8 ଓ d = 1 ହେଲେ ପଦଗୁଡ଼ିକ a – 5d = 8 – 5 = 3, a – 3d = 8 – 3 = 5,
a – d = 8 – 1 = 7, a + d = 8 + 1 = 9, a + 3d = 8 + 3 = 11, a + 5d = 8+ 5 = 13,
a = 8 ଓ d = -1 ହେଲେ ପଦଗୁଡ଼ିକ a – 5d = 8 – 5 (-1) = 8 + 5 = 13, a – 3d = 8 – 3 (- 1)
= 8 + 3 = 11, a – d = 8 – (- 1) = 9
a + d = 8+ (-1) = 7, a + 3d = 8 + 3 (- 1) = 8 – 3 = 5
a + 5d = 8 +5(-1) = 8 – 5 = 3
∴ A.P.ର ପଦତ୍ରୟ 3, 5, 7, 9, 11, 13 ବା 13, 11, 9, 7, 5, 3 ।

Question 13.
ଏକ ସମାନ୍ତର ଅନୁକ୍ରମରେ ଅବସ୍ଥିତ ତିନୋଟି ପଦର ଯୋଗଫଳ 21 ଏବଂ ସେମାନଙ୍କ ବର୍ଗର ଯୋଗଫଳ 155; ପଦଗୁଡ଼ିକ କେତେ ?
ସମାଧାନ :
ମନେକର ସମାନ୍ତର ଅନୁକ୍ରମର ଥ‌ିବା ତିନୋଟି ପଦ a + d, a, a + 3d ।
ପ୍ରଶ୍ନନୁସାରେ, a – d + a + a + d = 21 ⇒ 3a = 21 ⇒ a = \(\frac{21}{3}\) = 7
ପୁନଶ୍ଚ a (a – d)² + a² + (a + d)² = 155 ⇒ a² + (a – d)² + (a + d)² = 155
⇒ a² + 2 (a² + d²) = 155 ⇒ 7² + 2 (7² + d²) = 155
⇒ 2 (49 + d²) = 155 – 49 = 106 ⇒ 98 + 2d² = 106
⇒2d² = 106 – 98 ⇒ d² = \(\frac{8}{2}\) = 4 ⇒ d = = ±√4 = ±2
a = 7 ଓ d = 2 ହେଲେ ପଦଗୁଡ଼ିକ a – d = 7 – 2 = 5, a = 7, a + d = 7 + 2 = 9
a = 7 ଓ d = -2 ହେଲେ ପଦଗୁଡ଼ିକ a – d = 7 – (- 2) = 7 + 2 = 9,
a = 7, a + d = 7 + (- 2) = 7 – 2 = 5
∴ ସମାନ୍ତର ଅନୁକ୍ରମର ପଦତ୍ରୟ 5, 7, 9 ବା 9, 7, 5 ।

Question 14.
ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜର ବାହୁଗୁଡ଼ିକର ଦୈର୍ଘ୍ୟ ଏକ ସମାନ୍ତର ଅନୁକ୍ରମରେ ଥିଲେ ପ୍ରମାଣ କର ଯେ, ସେମାନଙ୍କର ଅନୁପାତ 3 : 4 : 5 ହେବ ।
ସମାଧାନ :
ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜର ବାହୁତ୍ରୟ ସମାନ୍ତର ଅନୁକ୍ରମରେ ଅବସ୍ଥିତ ।
ମନେକର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ a – d, a, a + d ।
ପ୍ରଶ୍ନନୁସାରେ, (a – d)² + a² = (a + d)² ⇒ (a + d)² – (a – d)² = a²
⇒ (a + d + a + d) (a + d – a + d) = a² ⇒ 2 × 2d = a² ⇒ a = 4d
⇒ ସମକୋଣୀ ତ୍ରିଭୁଜର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ, a – d = 4d – d = 3d, a = 4d,
a + d = 4d + d = 5d
ବାହୁଗୁଡ଼ିକର ଦୈର୍ଘ୍ୟ ଅନୁପାତ = 3d : 4d : 5d = 3 : 4 : 5 (ପ୍ରମାଣିତ)

Question 15.
100 ରୁ କ୍ଷୁଦ୍ରତର ଏବଂ 5 ଦ୍ୱାରା ବିଭାଜ୍ୟ ସମସ୍ତ ଧନାତ୍ମକ ପୂର୍ଣ୍ଣସଂଖ୍ୟାମାନଙ୍କର ଯୋଗଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ମନେକର 100 ଠାରୁ କ୍ଷୁଦ୍ରତର ଏବଂ 5 ଦ୍ବାରା ବିଭାଜ୍ୟ ସମସ୍ତ ଧନାତ୍ମକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟାର ଯୋଗଫଳ = S
S = 5 + 10 + 15 ……… + 95
ଏଠାରେ a = 5, d = 5, n = \(\frac{95}{5}\) = 19
S_n = \(\frac{n}{2}\) {2a + (n – 1) d}
= \(\frac{19}{2}\) {2 × 5+ (19 – 1) 5} = \(\frac{19}{2}\) (10 + 90) = \(\frac{19}{2}\) × 100 = 19 × 50 = 950
∴ ନିର୍ଦେୟ ଯୋଗଫଳ = 950

Question 16.
200 ରୁ କ୍ଷୁଦ୍ରତର ଓ 3 ଦ୍ଵାରା ଅବିଭାଜ୍ୟ ସମସ୍ତ ଧନାତ୍ମକ ପୂର୍ବସଂଖ୍ୟାମାନଙ୍କର ଯୋଗଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ମନେକର 1 ଠାରୁ ଆରମ୍ଭ କରି 200ରୁ କ୍ଷୁଦ୍ରତର ସମସ୍ତ ଧନାତ୍ମକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟାର ଯୋଗଫଳ = S₁
S₁ = 1 + 2 + 3 + 4 ……. + 199 = \(\frac{199×200}{2}\) = 199 × 100 = 19900
ପୁନଶ୍ଚ 200 ଠାରୁ କ୍ଷୁଦ୍ରତର 3 ଦ୍ଵାରା ବିଭାଜ୍ୟ ସମସ୍ତ ଧନାତ୍ମକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟାର ଯୋଗଫଳ
S₂ = 3 + 6 + 9 ………. + 198
ଏଠାରେ a = 3, d = 6-3 = 3, n = \(\frac{198}{3}\) = 66
S₂ = \(\frac{n}{2}\) {2a + (n – 1) d} = \(\frac{66}{2}\) {2 × 3 + (66 – 1) × 3}
= 33 {6 + 65 × 3) = 33 × (6 + 195) = 33 × 201 = 6633
200 ଠାରୁ କ୍ଷୁଦ୍ରତର 3 ଦ୍ଵାରା ଅବିଭାଜ୍ୟ ସମସ୍ତ ଧନାତ୍ମକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟାର ଯୋଗଫଳ
= S = S₁ – S₂ = 19900 – 6633 = 13267

Question 17.
15 କୁ ଏପରି 3 ଭାଗରେ ବିଭକ୍ତ କର ଯେପରିକି ସେମାନେ ଏକ ସମାନ୍ତର ଅନୁକ୍ରମରେ ରହିବେ ଓ ସେମାନଙ୍କର ଗୁଣଫଳ 120 ହେବ ।
ସମାଧାନ :
15କୁ ଏପରି ତିନି ଭାଗରେ ବିଭକ୍ତ କରାଯିବ ଯେପରି ସେମାନେ A.P.ରେ ରହିବେ ।
ମନେକର ସଂଖ୍ୟା ତ୍ରୟ a – d, a, a + d ।
ପ୍ରଶାନୁସାରେ, a – d + a + a + d = 15 ⇒ 3a = 15 ⇒ a = 5
ପୁନଶ୍ଚ (a – d) a (a + d) = 120
⇒ 5 (5² – d²) = 120 ⇒ 25 – d² = \(\frac{120}{5}\) ⇒ d² = 25 – 24
⇒ d² = 1 = d = +1
a=5 ଓ d = 1 ହେଲେ a – d = 5 – 1 = 4, a = 5, a + d = 5 + 1 = 6
a = 5 ଓ d = -1 ହେଲେ a – d = 5 – (- 1) = 5 + 1 = 6, a= 5,
a + d = 5 + (- 1) = 5 – 1= 4
∴ ସଂଖ୍ୟାତ୍ରୟ 4, 5, 6 ବା 6, 5,4 ।

Question 18.
A.P. ରେ ଥ‌ିବା ତିନୋଟି ପଦର ଯୋଗଫଳ 15 ଏବଂ ପ୍ରାନ୍ତ ପଦଦ୍ୱୟର ବର୍ଗର ଯୋଗଫଳ 58 ହେଲେ ପଦତ୍ରୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ମନେକର A.P. ରେ ଥ‌ିବା ପଦ ତିନୋଟି a – d, a, a + d ।
ପ୍ରଶ୍ନନୁସାରେ, a – d + a + a + d = 15 ⇒ 3a = 15 ⇒ a = \(\frac{15}{3}\) = 5
ପୁନଶ୍ଚ (a – d)² + (a + d)² = 58 ⇒ 2 (a² + d²) = 58
⇒ 5²+ d² = \(\frac{58}{2}\) ⇒ d² = 29 – 25 = 4 ⇒ d = ± √4 = ±2
a = 5 ଓ d = 2 ହେଲେ ପଦତ୍ରିୟ a – d = 5 – 2 = 3, a = 5, a + d = 5 + 2 = 7 ̧
a = 5 ଓ d = -2 ହେଲେ ପଦତ୍ରିୟ a – d = 5 – (- 2) = 5 + 2 = 7, a = 5,
a + d = 5 + (-2) = 3 ।
∴ A.P.ର ପଦତ୍ରୟ 3, 5, 7 ବା 7, 5, 3 ।

Question 19.
A.P. ରେ ଥିବା ଚାରୋଟି ପଦ ମଧ୍ୟରୁ ପ୍ରାନ୍ତ ପଦ ଦ୍ଵୟର ଯୋଗଫଳ 8 ଏବଂ ମଧ୍ୟ ପଦ ଦ୍ଵୟର ଗୁଣଫଳ 15 ହେଲେ ପଦଗୁଡ଼ିକ ସ୍ଥିର କର ।
ସମାଧାନ :
ମନେକର A.P.ରେ ଥ‌ିବା ଚାରୋଟି ପଦ a – 3d, a – d, a + d ଓ a + 3d ।
ପ୍ରଶ୍ନନୁସାରେ, a – 3d + a + 3d = 8⇒ 2a = 8 ⇒ a = \(\frac{8}{2}\) = 4
ପୁନଶ୍ଚ (a – d) (a + d) = 15 ⇒ a² – d² = 15 ⇒ 4² – 15 = d²
⇒ d² = 16 – 15 = 1 ⇒ d = ±√1 = ±1
a = 4 ଓ d = 1 ହେଲେ ପଦତ୍ରିୟ a – 3d = 4 – 3 (1) = 4 – 3 = 1
a – d = 4 – 1 = 3, a + d = 4 + 1 = 5
a + 3d = 4 + 3 · 1 = 4 + 3 = 7
a =4 ଓ d = 1 ହେଲେ ପଦତ୍ରିୟ a – 3d = 4 – 3 (-1) = 4 + 3 = 7,
a – d = 4 – (-1) = 4 + 1 = 5,
a + d = 4 + (-1) = 3 ଏବଂ a + 3d = 4 + 3 (- 1) = 4 – 3 = 1
∴ A.P.ର ଥ‌ିବା ପଦତ୍ରୟ 1, 3, 5, 7 ବା 7, 5, 3, 1 ।

Question 20.
A.P. ରେ ଥ‌ିବା ତିନୋଟି ରାଶିମାଳାର n ସଂଖ୍ୟକ ପଦମାନଙ୍କର ସମଷ୍ଟି S₁ S₂ ଏବଂ S₃ । ପ୍ରତ୍ୟେକ ରାଶିମାଳାର ପ୍ରଥମ ପଦ 1 ଏବଂ ସାଧାରଣ ଅନ୍ତର ଯଥାକ୍ରମେ 1, 2, 3 ହେଲେ ପ୍ରମାଣ କର ଯେ, S₁ + S₃ = 2S₂ ।
ସମାଧାନ :
A.P. ରେ ଥିବା ତିନୋଟି ରାଶିମାଳାର n ସଂଖ୍ୟକ ପଦମାନଙ୍କର ସମଷ୍ଟି S₁ S₂ ଏବଂ S₃ ।
ପ୍ରତ୍ୟେକ ରାଶିମାଳାର ପ୍ରଥମ ପଦ = a
ପ୍ରଥମ ରାଶିମାଳାର d = 1, ଦ୍ୱିତୀୟ ରାଶିମାଳାର d = 2, ତୃତୀୟ ରାଶିମାଳାର d = 3
S₁ = \(\frac{n}{2}\) {2 ×1 + (n – 1) 1} = \(\frac{n}{2}\) (n + 1)
S₂ = \(\frac{n}{2}\) {2 ×1 + (n – 1) 2} = n²
ଏବଂ S₃ = \(\frac{n}{2}\) {2 ×1 + (n – 1) 3} = \(\frac{n}{2}\) (3n – 1)
L.H.S. = S₁ + S₃ = \(\frac{n}{2}\) (n + 1) + \(\frac{n}{2}\) (3n – 1)
= \(\frac{n}{2}\) {n + 1 + 3n – 1}
R.H.S. = 2S₂ = 2 × n² = 2n²
∴ L.H.S = R.H.S. (ପ୍ରମାଣିତ)

Question 21.
ଏକ A.P. ର p-ତମ, ୟୁ-ତମ ଏବଂ r-ତମ ପଦଗୁଡ଼ିକର ମାନ ଯଥାକ୍ରମେ a, b ଏବଂ c ହେଲେ ପ୍ରମାଣ 6, a (q – r) + b (r -p) + c (p – q) = 0 |
ସମାଧାନ :
ମନେକର A.P. ର ପ୍ରଥମ ପଦ = x, ସାଧାରଣ ଅନ୍ତର = d
t = x + (p – 1) d = a ……… (i)
t = x + (q – 1) d = b ……… (ii)
t = x + (r – 1) d = c …….(iii)
ସମୀକରଣ (i)ରୁ (ii)କୁ ବିୟୋଗ କଲେ,

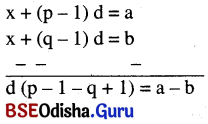
⇒ d (p – q) = a – b ⇒ d = \(\frac{a – b}{p – q}\) …… (iv)
ସେହିପରି (ii)ରୁ (iii)କୁ ବିୟୋଗ କଲେ ଆମେ ପାଇବା d = \(\frac{b – c}{q – r}\) …… (v)
ସମୀକରଣ (iv) ଓ (v) ରୁ ⇒ \(\frac{a – b}{p – q}=\frac{b – c}{q – r}\) ⇒ (a – b) (q- r) = (b -c) (p – q)
⇒ a (q – r) – b(q – r) = b(p – q) – c (p – q)
⇒ a (q – r) – b(q – r) = b (p – q) + c (p – q) = 0
⇒ a (q – r) – b(q – r + p – q) + c (p – q) = 0
⇒ a (q – r) – b(p – r) + c (p – q) = 0
⇒ a (q – r) – b(r – p) + c (p – q) = 0 (ପ୍ରମାଣିତ)
ବି.ଦ୍ର. : (i) ରୁ a = x + (p – 1)d
∴ a(q – r) = x (q – r) + (p – 1) (q – r)d
ସେହିପରି b(r- p) = x (r – p) + (q – 1) (r – p)d ଏବଂ
c (p – q) = x (p – q) + (r – 1) (p – q) d
ଯୋଗକଲେ a (q – r) + b (r- p) + c (p -q) = 0 ପାଇବା

Question 22.
ତିନୋଟି ସଂଖ୍ୟା a, b, ୯ ସମାନ୍ତର ପ୍ରଗତିରେ ରହିଲେ ପ୍ରମାଣ କର ଯେ ନିମ୍ନରେ ପ୍ରଦତ୍ତ ସଂଖ୍ୟା ତ୍ରୟ ମଧ୍ୟ ସମାନ୍ତର ପ୍ରଗତିରେ ରହିବେ ।
(i) \(\frac{1}{bc},\frac{1}{ca},\frac{1}{ab}\)
(ii) b+c, c + a, a + b
(iii) b+c-a, c + a-b, a + b-c
(iv) \(\frac{1}{a}(\frac{1}{b}+\frac{1}{c}),\frac{1}{b}(\frac{1}{c}+\frac{1}{a}),\frac{1}{c}(\frac{1}{a}+\frac{1}{b})\)
(v) a² (b+c), b² (c + a), c²(a + b)
ସମାଧାନ :
(i) a, b, c ସମାନ୍ତର ପ୍ରଗତିରେ ଅବସ୍ଥିତ ।
ପ୍ରତ୍ୟେକ ପଦକୁ abc ଦ୍ବାରା ଭାଗକଲେ \(\frac{1}{abc},\frac{1}{abc},\frac{1}{abc}\) ସମାନ୍ତର ପ୍ରଗତିରେ ରହିବେ ।
⇒ \(\frac{1}{bc},\frac{1}{ca},\frac{1}{ab}\) (ପ୍ରମାଣିତ)

(ii) a, b, c ସମାନ୍ତର ପ୍ରଗତିରେ ଅବସ୍ଥିତ ।
(a + b + c) ବିୟୋଗ କଲେ ବିୟୋଗଫଳ A.P.ରେ ରହିବ ।
ଅର୍ଥାତ୍ (a+b+c), b – (a + b + c), c (a + b + c) A.P.ରେ ରହିବ ।
⇒ – (b + c), -(c + a), -(a + b) A.P.ରେ ରହିବ ।
⇒ b + c, c + a, a + b ସମାନ୍ତର ପ୍ରଗତିରେ ରହିବେ । (ପ୍ରତ୍ୟେକ ପଦକୁ –1 ଦ୍ଵାରା ଗୁଣିଲେ)

(iii) a, b, c A.P.ରେ ଅବସ୍ଥିତ ।
⇒ 2a, 2b, 2c ମଧ୍ଯ A.P. ରେ ରହିବେ (ପ୍ରତ୍ୟେକ ପଦରେ 2 ଗୁଣନ କଲେ ।)
ପ୍ରତ୍ୟେକରୁ (a + b + c) ପଦକୁ ବିୟୋଗ କଲେ ବିୟୋଗଫଳ A.P ରେ ରହିବ ।
⇒ 2a – (a+b+c), 2b – (a + b + c), 2c – (a + b + c) A.P.ରେ ରହିବ ।
⇒ (b + c – a), (c + a – b), (a + b – c) A.P.ରେ ରହିବ ।
⇒ b+c-a, c+a-b, a+b-c A.P.ରେ ରହିବ ।

(iv) a, b, c A.P.ରେ ଅବସ୍ଥିତ ।
A.P.ର ପ୍ରତ୍ୟେକ ପଦରେ (-1) ଗୁଣନ କଲେ, -a, -b, -c A.P.ରେ ରହିବ ।
A.P.ର ପ୍ରତ୍ୟେକ ପଦରେ a + b + c ଯୋଗକଲେ
a + b + c – a, a + b + c – b, a + b + c – c A.P.ରେ ରହିବ ।
∴ b + c, c + a, a + b A.P.ରେ ରହିବ ।
A.P.ର ପ୍ରତ୍ୟେକ ପଦକୁ abc ଦ୍ଵାରା ଭାଗକଲେ \(\frac{b + c}{abc},\frac{c + a}{abc},\frac{a + b}{abc}\) A.P.ରେ ରହିବ ।
⇒ \(\frac{1}{a}(\frac{b + c}{bc}),\frac{1}{b}(\frac{c + a}{ac}),\frac{1}{c}(\frac{a + b}{ab})\) A.P.ରେ ରହିବ ।
⇒ \(\frac{1}{a}(\frac{1}{b}+\frac{1}{c}),\frac{1}{b}(\frac{1}{c}+\frac{1}{a}),\frac{1}{c}(\frac{1}{a}+\frac{1}{b})\) A.P.ରେ ରହିବ ।

(v) a, b, c A.P.ରେ ଅବସ୍ଥିତ ।
A.P.ର ପ୍ରତ୍ୟେକ ପଦରେ ab + bc + ca ଗୁଣନ କଲେ ଗୁଣଫଳ A.P.ରେ ରହିବ ।
a (ab + bc + ca), b (ab + bc + ca), c (ab + bc + ca) A.P.ରେ ରହିବେ ।
a²b+ abc + ca², ab²+ b²c + abc, abc + bc² + c²a A.P.ରେ ରହିବ ।
= A.P.ର ପ୍ରତ୍ୟେକ ପଦରୁ abc ବିୟୋଗ କଲେ ଲବ୍‌ଧ ଅନୁକ୍ରମ A.P.ରେ ରହିବ ।
a²b + ca², ab² + b²c, bc² + c²a A.P.ରେ ରହିବ ।
a²(b+c), b²(c + a), c²(a + b), A.P.ରେ ରହିବ ।

Question 23.
(i) \(\frac{1}{a},\frac{1}{b},\frac{1}{c}\) ରେ ରହିଲେ ଏବଂ a + b + c ≠ 0 ହେଲେ, ପ୍ରମାଣ କର ଯେ \(\frac{b + c}{a},\frac{c + a}{b},\frac{a + b}{c}\) ମଧ୍ୟ A.P. ରେ ରହିବେ ।
(ii) \(\frac{a}{b + c},\frac{b}{c + a},\frac{c}{a + b}\) ଅନୁକ୍ରମ A.P.ରେ ରହିଲେ ଏବଂ a + b + c ≠ 0 ହେଲେ ପ୍ରମାଣ କର ଯେ, \(\frac{1}{b + c},\frac{1}{c + a},\frac{1}{a + b}\) A.P.ରେ ରହିବେ ।
ସମାଧାନ :
(i) \(\frac{1}{a},\frac{1}{b},\frac{1}{c}\) A.P.ରେ ଅବସ୍ଥିତ । (a + b + c ≠ 0)
⇒ A.P. ର ପ୍ରତ୍ୟେକ ପଦରେ a + b + c ଗୁଣନ କଲେ,
\(\frac{a+b+c}{a},\frac{a+b+c}{b},\frac{a+b+c}{c}\) A.P.ରେ ରହିବ ।
⇒ \(\frac{a}{a}+\frac{b+c}{a}, \frac{c+a}{b}+\frac{b}{b}, \frac{a+b}{c}+\frac{c}{c}\)
⇒ \(1+\frac{b+c}{a}, \frac{c+a}{b}+1, \frac{a+b}{c}+1\) A.P.ରେ ରହିବ ।
⇒ \(\frac{b+c}{a}, \frac{c+a}{b}, \frac{a+b}{c}\) A.P.ରେ ରହିବ । (ପ୍ରତ୍ୟେକ ପଦରୁ 1 ବିୟୋଗ କଲେ ।) (ପ୍ରମାଣିତ)

Question 24.
ଯଦି କୌଣସି A.P.ର ପ୍ରଥମ ପଦ a ଏବଂ ଶେଷ ପଦ l ହୁଏ ପ୍ରମାଣ କର ଯେ, ଅନୁକ୍ରମର ପ୍ରଥମରୁ r ତମ ପଦ ଏବଂ ଶେଷରୁ r ତମ ପଦର ସମଷ୍ଟି, ପ୍ରଥମ ଓ ଶେଷ ପଦର ସମଷ୍ଟି ସହିତ ସମାନ ।
ସମାଧାନ :
A.P.ର ପ୍ରଥମପଦ = a, ଶେଷ ପଦ = l
ମନେକର ସାଧାରଣ ଅନ୍ତର = d ।
∴ A.P. ଟି a, a + d, a + 2d, a + 3d, …….. l + 2d, l + d, l
ପ୍ରଥମରୁ rତମ ପଦ = a + (r – 1) d
ଶେଷ r ତମ ପଦର a = l, d = -d
t_r = l + (r – 1 ) (-d)
∴ ପ୍ରଥମରୁ r ତମ ପଦ + ଶେଷରୁ r ତମ ପଦ = [a + (r – 1) d] + [l + (r – 1) (- d)]
= a + (r – 1) d + l – (r – 1) d = a + l
∴ ପ୍ରଥମ ଓ ଶେଷ ପଦର ସମଷ୍ଟି = a + l
∴ ପ୍ରଥମରୁ r ତମ ପଦ ଓ ଶେଷରୁ 1 ତମ ପଦର ସମଷ୍ଟି = ପ୍ରଥମ ଓ ଶେଷ ପଦର ସମଷ୍ଟି ।
ବିକଳ୍ପ ପ୍ରଣାଳୀ : ପ୍ରଥମରୁ 1 ତମ ପଦ (t) = a + (r – 1)d
ଶେଷରୁ r ତମ ପଦ = ପ୍ରଥମରୁ (n – r + 1) ତମ ପଦ
= t_n-r+1 = a + {(n – r+1) – 1}d = a + (n – r)d
∴ t_r + _n-r + 1 = a = (r – 1 )d + a + (n – r) d = 2a + (n – 1)d = a + {a + (n – 1)d} = a + 1

Question 25.
ଗୋଟିଏ ସମାନ୍ତର ପ୍ରଗତିର ପ୍ରଥମ p ସଂଖ୍ୟକ ପଦର ସମଷ୍ଟି r, ପ୍ରଥମ q ସଂଖ୍ୟକ ପଦର ସମଷ୍ଟି s ଏବଂ ସାଧାରଣ ଅନ୍ତର । ହେଲେ ପ୍ରମାଣ କର ଯେ, \(\frac{r}{p}-\frac{s}{q}\) = (p – q) \(\frac{d}{2}\) ହେବ ।
ସମାଧାନ :
ଗୋଟିଏ ସମାନ୍ତର ପ୍ରଗତିର S_p = x ଏବଂ S_q = s
ସାଧାରଣ ଅନ୍ତର = d । ମନେକର ପ୍ରଥମ ପଦ = a
.. ପ୍ରଥମ p-ସଂଖ୍ୟକ ପଦର ସମଷ୍ଟି = S_p = \(\frac{p}{2}\) {2a + (p – 1) d}
ପ୍ରଶାନୁସାରେ, \(\frac{p}{2}\) {2a + (p – 1) d} = r ⇒ 2a + (p – 1) d = \(\frac{2r}{p}\) …….(i)
.. ପ୍ରଥମ q-ସଂଖ୍ୟକ ପଦର ସମଷ୍ଟି = S_q = \(\frac{q}{2}\) {2a + (q – 1) d}
ପୁନଶ୍ଚ, \(\frac{q}{2}\) {2a + (q – 1) d} = s ⇒ 2a + (q – 1) d = \(\frac{2s}{q}\) …….(ii)
ସମୀକରଣ (i)ରୁ (ii)କୁ ବିୟୋଗ କଲେ,

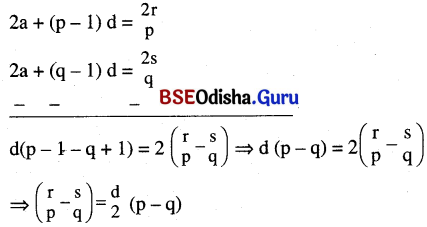
Question 26.
ଗୋଟିଏ ସମାନ୍ତର ଶ୍ରେଣୀର ପ୍ରଥମ p, q, r ସଂଖ୍ୟକ ପଦର ସମଷ୍ଟି a, b, c ହେଲେ ପ୍ରମାଣ କର ଯେ, \(\frac{a}{p}\) (q – r) + \(\frac{b}{q}\) (r – p) + \(\frac{c}{r}\) (p – q) = 0 ହେବ ।
ସମାଧାନ :
ଗୋଟିଏ ସମାନ୍ତର ଶ୍ରେଣୀର ପ୍ରଥମ p, q, r ସଂଖ୍ୟକ ପଦର ସମଷ୍ଟି a, b, c ।
ମନେକର A.P.ର ପ୍ରଥମ ପଦ = x ଓ ସାଧାରଣ ଅନ୍ତର = d
S_p = \(\frac{p}{2}\) {2a + (p – 1) d} = a ⇒ 2x + (p – 1) d = \(\frac{2a}{p}\) ……(i)
S_q = \(\frac{q}{2}\) {2a + (q – 1) d} = b ⇒ 2x + (q – 1) d = \(\frac{2b}{q}\) ……(ii)
S_r = \(\frac{r}{2}\) {2a + (r – 1) d} = c ⇒ 2x + (r – 1) d = \(\frac{2c}{r}\) ……(iii)
ସମୀକରଣ (i)ରୁ (ii)କୁ ବିୟୋଗ କଲେ,


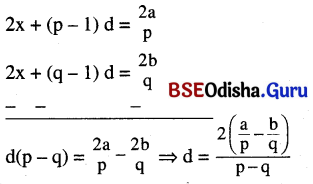
ବି.ଦ୍ର. : (i) ରୁ 2 =x + \(\frac{1}{2}\)(p – 1)d ⇒ \(\frac{a}{p}\) (q – r) = x(q – r) + \(\frac{1}{2}\) (p – 1)(q – r)d
ସେହିପର \(\frac{b}{q}\)(r – p) = x(r – p) + \(\frac{1}{2}\) (q – 1)(r – p)d
c(p – q) = x(p – q) + 2(r – 1)(p – q)d
ଯୋଗକଲେ \(\frac{a}{p}\) (q – r) + \(\frac{b}{q}\) (r – p) + \(\frac{c}{r}\) (p – q) = 0 ହେବ ।

Question 27.
କୌଣସି A.P.ର t = q, t = p ହେଲେ ପ୍ରମାଣ କର ଯେ t = p + q – m ।
ସମାଧାନ :
ମନେକର A.P.ର ପ୍ରଥମ ପଦ = a ଓ ସାଧାରଣ ଅନ୍ତର = d
ଏକ A.P.ର t_p = q ⇒ a + (p – 1)d = q … (i)
⇒ t_q = p ⇒ a + (q – 1)d = p … (ii)
t_p – t_q = q – p ⇒ a + (p – 1)d – a + (q – 1)d = q – p
⇒ d(p – 1 – q + 1) = q – p ⇒ d(p – q) = q – p
⇒ d = \(\frac{q-p}{p-q}=\frac{-(p-q)}{p-q}=-1\)
‘d’ର ମାନ (i) ରେ ବସାଇଲେ a + (p – 1) d = q
⇒ a + (p – 1) (-1) = q ⇒ a – p + 1 = q
⇒ a = p + q – 1
:. t = a + (m – 1)d = p + q – 1 +(m – 1)(-1)
= p + q – 1 – m + 1 = p + q – m

Question 28.
କୌଣସି A.P.ର S_m = n, S_n = m ହେଲେ, ପ୍ରମାଣ କର ଯେ S_m+n = -(m + n) ହେବ ।
ସମାଧାନ :
ମନେକର A.P.ର ପ୍ରଥମ ପଦ = a, ସାଧାରଣ ଅନ୍ତର = d
S_m = n ⇒ \(\frac{m}{2}\) {2a + (m – 1) d} = n ⇒ am + (m² – m) \(\frac{d}{2}\) = n ……(i)
S_n = m ⇒ \(\frac{n}{2}\) {2a + (n – 1) d} = m ⇒ an + (n² – n) \(\frac{d}{2}\) = m ……(ii)
ସମୀକରଣ (i)ରୁ (ii)କୁ ବିୟୋଗ କଲେ