BSE Odisha 10th Class Maths Solutions Algebra Chapter 3 ସମାନ୍ତର ପ୍ରଗତି Ex 3(b)

Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 3 ସମାନ୍ତର ପ୍ରଗତି Ex 3(b) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Algebra Chapter 3 ସମାନ୍ତର ପ୍ରଗତି Ex 3(b)

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(a) \(\frac{1}{15×16}=…..- \frac{1}{16}\)
(b) \(\frac{1}{12×11}=- \frac{1}{11}\) – …….
(c) \(\frac{1}{n(n+1)}=…..- \frac{1}{n+1}\)
(d) \(\frac{1}{(n+1)n}=- \frac{1}{n}\) – …….
(e) 5 ଓ 9 ମଧ୍ୟରେ ଥ‌ିବା ସମାନ୍ତର ମଧ୍ଯକଟି …..
(f) x ଓ 7 ମଧ୍ଯସ୍ଥ ସମାନ୍ତର ମଧ୍ୟକଟି 5 ହେଲେ x = …..
(g) (a + b) 8 (a – b) ମଧ୍ୟରେ ଥ‌ିବା ସମାନ୍ତର ମଧ୍ଯକଟି ………
(h) ଦୁଇଟି ରାଶିର A.M. 11, ଯଦି ଗୋଟିଏ ରାଶି 7 ହୁଏ, ତେବେ ଅନ୍ୟଟି ……….
ଉ-
(a) \(\frac{1}{15}\)
(b) \(\frac{1}{12}\)
(c) \(\frac{1}{n}\)
(d) \(\frac{1}{n+1}\)
(e) 7
(f) 3
(g) a
(h) 15

ବ୍ୟାଖ୍ୟା ସହ ଉତ୍ତର:
(a) \(\frac{1}{15 \times 16}=\frac{1}{15}-\frac{1}{16}\left[\text { R.H.S. }=\frac{1}{15}-\frac{1}{16}=\frac{16-15}{15 \times 16}=\frac{1}{15 \times 16}=\text { L.H.S. }\right]\)
(b) \(\frac{1}{12×11}=\frac{1}{11}-\frac{1}{12}\)
(c) \(\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}\)
(d) \(\frac{1}{(n+1)n}=\frac{1}{n}-\frac{1}{n+1}\)
(e) 5 ଓ 9 ମଧ୍ୟରେ ଥ‌ିବା ସମାନ୍ତର ମଧ୍ଯକଟି = \(\frac{5+9}{2}=\frac{14}{2}=7\)
(f) x ଓ 7 ମଧ୍ଯସ୍ଥ ସମାନ୍ତର ମଧ୍ୟକଟି 5 ହେଲେ x = \(\frac{x+7}{2}\) = 5 ⇒ x = 10 – 7 = 3
(g) (a + b) 8 (a – b) ମଧ୍ୟରେ ଥ‌ିବା ସମାନ୍ତର ମଧ୍ଯକଟି \(\frac{a+b+a-b}{2}=\frac{2a}{2}\) = a
(h) ଦୁଇଟି ରାଶିର A.M. 11, ଯଦି ଗୋଟିଏ ରାଶି 7 ହୁଏ, ତେବେ ଅନ୍ୟଟି x
∴ \(\frac{x+7}{2}\) = 11 ⇒ x = 22 – 7 = 15

Question 2.
ନିମ୍ନଲିଖୂତ ଅନୁକ୍ରମଗୁଡ଼ିକର ସମଷ୍ଟି ନିଶ୍ଚୟ କର ।
(a) \(\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}\) ……..20ଟି ପଦ ପର୍ଯ୍ୟନ୍ତ;
(b) \(\frac{1}{5×6}+\frac{1}{6×7}+\frac{1}{7×8}\) ……..16ଟି ପଦ ପର୍ଯ୍ୟନ୍ତ
ସମାଧାନ :
(a) \(\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}\) ……..20ଟି ପଦ ପର୍ଯ୍ୟନ୍ତ;

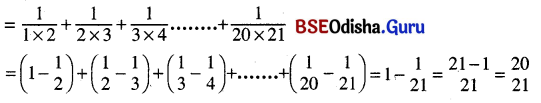
(b) \(\frac{1}{5×6}+\frac{1}{6×7}+\frac{1}{7×8}\) …….16ଟି ପଦ ପର୍ଯ୍ୟନ୍ତ ସମଷ୍ଟି।

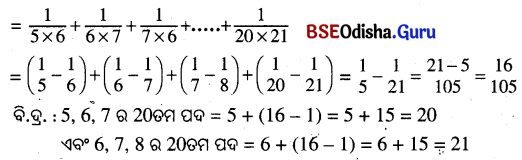
Question 3.
(a) 7 × 15 + 8 × 20 + 9 × 25 + …..ର t_n ନିର୍ଣ୍ଣୟ କର ।
(b) 6Σn²+4Σn³ ର ସରଳୀକୃତ ମାନ ନିର୍ଣ୍ଣୟ କର ।
(c) 1 × 2 + 2 × 3 + 3 × 4 ….. + n (n + 1) ପାଇଁ S_n ଓ S₂₀ ନିର୍ଣ୍ଣୟ କର ।
(d) 1 × 3 + 2 × 4 + 3 × 5 …… t_n, S_n ଓ S₁₀ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
(a) 7 × 15 + 8 × 20 + 9 × 25 …….ର t_n
ରାଶିମାଳାର ପ୍ରଥମ ଗୁଣନୀୟକଗୁଡ଼ିକ 7,8, 9, A.P.ରେ ଅଛନ୍ତି ।
a = 7, d = 8 – 7 = 9 – 8 = 1
∴ t_n = a + (n – 1) d = 7 + (n – 1 ) 1 = 7 + n – 1 = n + 6
ରାଶିମାଳାଟିର ଦ୍ଵିତୀୟ ଗୁଣନୀୟକଗୁଡ଼ିକ 15, 20, 25 ……. A.P. ଅଛନ୍ତି ।
a = 15, d = 5, t_n = a + (n – 1)d = 15 + (n – 1)5 = 15 + 5n – 5 = 5n + 10
∴ 7 × 15 + 8 × 20 + 9 × 25 + …..ର t_n = (n + 6)(5n + 10)
= 5(n + 6)(n + 2) = 5(n² + 8n + 12)

(b) 6Σn²+4Σn³ = \(\frac{6 \times n(n+1)(2 n+1)}{6}+4\left\{\frac{n(n+1)}{2}\right\}^2\)
= n(n + 1)(2n + 1) + n²(n + 1)²
= n(n + 1){(2n+ I + n(n + 1)} = n(n + 1)(n² + 3n + 1)

(c) 1 × 2 + 2 × 3 + 3 × 4 ….. + n (n + 1)
ଏଠାରେ t_n = n(n + 1)= n² + n
S_n = Σn² + Σn = \(\frac{n(n+1)(2 n+1)}{6}+\frac{n(n+1)}{2}\)
= n(n+1){\(\frac{2 n +1}{6}+\frac{1}{2}\)}
= (n² + n){\(\frac{2 n +1+3}{6}\)} = \(\frac{(n² + n)(2 n +4)}{6}\)
= \(\frac{n (n+1)(n+2)}{3}\)
S₂₀ = \(\frac{20×21×22}{3}\) = 3080

(d) 1 × 3 + 2 × 4 + 3 × 5 ……
ପ୍ରତ୍ୟେକ ପଦର ପ୍ରଥମ ଗୁଣନୀୟକ 1, 2, 3, 4 ……. । ଏହାର t = n
ପ୍ରତ୍ୟେକ ପଦର ଦ୍ଵିତୀୟ ଗୁଣନୀୟକଗୁଡ଼ିକ ହେଲେ 3, 4, 5, …
0166 a = 3, d=4-35-4=1
t =
= a + (n – 1 ) d = 3 + (n – 1) 1 = n + 2
∴ ରାଶିଟିର t = n(n + 2) = n² + 2n
S_n = Σn² + 2Σn = \(\frac{n(n+1)(2 n+1)}{6}+\frac{2 n(n+1)}{2}\)
= n(n+1)(\(\frac{2 n +1}{6}+1\)) = \(\frac{n(n+1)(2 n +7)}{6}\)
S_n = \(\frac{n(n+1)(2 n +7)}{6}\)
S₁₀ = \(\frac{n(n+1)(2 n +7)}{6}\) = \(\frac{10×(10+1)(2×10 +7)}{6}\) = \(\frac{10×11×27}{6}\) \(\frac{2970}{6}\) = 495

Question 4.
ନିମ୍ନଲିଖତ ଶ୍ରେଣୀଗୁଡ଼ିକର n ସଂଖ୍ୟକ ପଦ ପର୍ଯ୍ୟନ୍ତ ଯୋଗଫଳ ନିର୍ଣ୍ଣୟ କର ।
(a) 1.1 + 2.3 + 3.5 +4.7 + …….
(b) 1.3 +3.5 + 5.7 + 7.9 + …….
(c) 3.8 +6.11 + 9.14 + …….
(d) 1+ (1 + 3) + (1 + 3 + 5) +
(e) 1² + 4² + 7² + 10² + …….
(f) 2² + 4² +6² + 8² + …….
(g) 1 + 5 + 12 +22 + 35+…….
(h) 1² + (1² + 2²) + (1² + 2² + 3²) + (1² + 2² + 3² + 4²) + ……….
ସମାଧାନ :
(a) 1.1 + 2.3 + 3.5 + 4.7 + …..
ଦତ୍ତ ଶ୍ରେଣୀର ପ୍ରଥମ ଗୁଣନୀୟକଗୁଡ଼ିକ 1, 2, 3, 4 …….
ଏହାର t_n = n
ସେହିପରି ଦ୍ୱିତୀୟ ଶ୍ରେଣୀର ଗୁଣନୀୟକଗୁଡ଼ିକ 1, 3, 5, 7 ……. । ଏହାର a = 1, d = 3 − 1 = 2
ଏହାର t_n = 1 + (n – 1) × 2 = 2n – 1
ଦତ୍ତ ଶ୍ରେଣୀର t_n = n(2n – 1) = 2n² – n
S_n = 2Σn² – Σn = \(\frac{2n (n + 1)(2n + 1)}{6}-\frac{n(n+1)}{2}\)
= n(n+1)(\(\frac{4 n +2}{6}-\frac{1}{2}\)) = \(\frac{n(n+1)(4 n +2-3)}{6}\) = \(\frac{n(n+1)(4 n -1)}{6}\)
S_n = \(\frac{n(n+1)(4 n -1)}{6}\)

(b) 1.3 + 3.5 + 5.7 + 7.9 + …….
ଦତ୍ତ ଶ୍ରେଣୀର ପ୍ରତ୍ୟେକ ପଦର ପ୍ରଥମ ଗୁଣନୀୟକ 1, 3, 5, 7 ……. A.P. ଅଟନ୍ତି ।
t_n = 1 + (n – 1) 2 = 2n – 1
ଦତ୍ତ ଶ୍ରେଣୀର ପ୍ରତ୍ୟେକ ପଦର ଦ୍ୱିତୀୟ ଗୁଣନୀୟକ 3, 5, 7, 9,
ଏଠାରେ a = 3, d = 5 – 3 = 2
t_n = 3 + (n – 1) × 2 = 3 + 2n – 2 = 2n + 1

(c) 3.8 +6.11 + 9.14 + …….
ଶ୍ରେଣୀର ପ୍ରତ୍ୟେକ ପଦର ପ୍ରଥମ ଗୁଣନୀୟକଗୁଡ଼ିକ 3, 6, 9, ……. A.P. ଅଟନ୍ତି ।
a = 3, d = 6 – 3 = 9 – 6 = 3, t = 3 + (n – 1 ) × 3 = 3n
ଦତ୍ତ ଶ୍ରେଣୀର ପ୍ରତ୍ୟେକ ପଦର ଦ୍ବିତୀୟ ଗୁଣନୀୟକଗୁଡ଼ିକ 8, 11, 14, …….
a = 8, d = 11-8 = 14 – 11 = 3
t_n = a + (n – 1) d = 8 + (n – 1) 3 = 8 + 3n – 3 = 3n + 5

(d) S_n = 1 + (1 + 3) + (1 + 3 + 5) + …….. + t_n
= 1 + (1 + 3) + (1 + 3 + 5) + …… +(1 + 3 + 5 + 7) …….
ଦତ୍ତ ଶ୍ରେଣୀର t_n = 1 + 3 + 5 + 7 +……. + n-ତମ ପଦ ପର୍ଯ୍ୟନ୍ତ
⇒ t_n = \(\frac{n}{2}\) {2·1 + (n – 1) 2} = \(\frac{n}{2}\) (2 + 2n – 2) = n²
⇒ S_n = Σn² = \(\frac{2n (n + 1)(2n + 1)}{6}\) = \(\frac{1}{6}\)n (n² + 3n + 1)

(e) 1² + 4² + 7² + 10² + …….
1, 4, 7, 10 ……… A.P.
a = 1, d= 4 – 1 = 7 – 4 = 3, t_n = 1 + (n – 1) × 3 = 1 + 3n – 3 = 3n – 2
ଦତ୍ତ ଶ୍ରେଣୀର t_n = (3n – 2)² = 9n² – 12n + 4
⇒ S_n = 9Σn² – 12Σn + 4Σ1 = \(\frac{9n (n + 1)(2n + 1)}{6}-12 \frac{n(n+1)}{2}+4n\)
= \(\frac{(9n²+9n) (2n+1)-36n²-36n+24n}{6}\)
= \(\frac{1}{6}\) (18n³ + 9n² + 18n² + 9n – 36n² – 36n + 24n)
= \(\frac{1}{6}\) (18n³ – 9n² – 3n)
= \(\frac{3}{6}\) (6n³ – 3n² – n)
= \(\frac{n}{2}\) (6n³ – 3n² – n)

(f) S_n = 2² + 4² +6² + 8² + ……. = 2²(1² + 2² +3² + 4² + ….. + t_n)
= \(\frac{4n(n + 1)(2n + 1)}{6}\) (∵ 1² + 2² +3² + 4² + ….. + n² = \(\frac{4n(n + 1)(2n + 1)}{6}\))
⇒ S_n = \(\frac{2}{3}\) n(n + 1)(2n + 1)

(g)

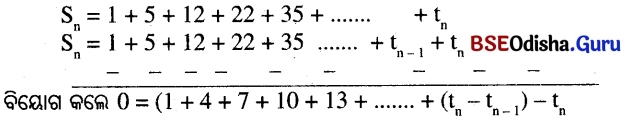
⇒ t_n = 1 + 4 +7 + 10 + 13 + ….. n ତମ ପଦ ପର୍ଯ୍ୟନ୍ତ
= \(\frac{n}{2}\) {2 + (n – 1) × 3}
= \(\frac{n}{2}\) {2 + 3n – 3}
= \(\frac{n}{2}\) {3n – 1}
= \(\frac{3}{2}\) n² – \(\frac{1}{2}\)n
S_n = \(\frac{3}{2}\) Σn² – \(\frac{1}{2}\) Σn
= \(\frac{3}{2}\) \(\frac{4n(n + 1)(2n + 1)}{6}\) – \(\frac{1}{2}\) \(\frac{n(n + 1)}{3}\)
= \(\frac{n(n + 1)(2n + 1)}{4}\) – \(\frac{n(n + 1)}{4}\)
= \(\frac{n(n + 1)}{4}\) (2n + 1 – 1) = \(\frac{n(n + 1)×2n}{4}\) = \(\frac{1}{2}\)n² (n+1)

(h) S_n = 1² + (1² + 2²) + (1² + 2² + 3²) + (1² + 2² + 3² + 4²) + ……….
t_n = (1²+ 2²+ 3² + ………. + n²)

Question 5.
15 ଓ 27 ମଧ୍ଯରେ (i) ଗୋଟିଏ ଓ (ii) ଦୁଇଗୋଟି ସମାନ୍ତର ମଧ୍ଯକ ସ୍ଥାପନ କର ।
ସମାଧାନ :
(i) 15 ଓ 27 ମଧ୍ଯରେ ଗୋଟିଏ ସମାନ୍ତର ମଧ୍ୟକ x = \(\frac{a+b}{2}=\frac{15+27}{2}=\frac{42}{2}=21\)

(ii) ମନେକର 15 ଓ 27 ମଧ୍ୟରେ ଅବସ୍ଥିତ ଥ‌ିବା ଦୁଇଟି ସମାନ୍ତର ମଧ୍ୟକ x₁ ଓ x₂।
ଏଠାରେ a = 15, b = 27, d = \(\frac{b-a}{3}=\frac{27-15}{3}=\frac{12}{3}=4\)
x₁ = a + d = 15 + 4 = 19, x₂ = a + 2d = 15 + 2 × 4 = 23
∴ 15 ଓ 27 ମଧ୍ୟରେ ଅବସ୍ଥିତ ଦୁଇଟି A.M. 19 ଓ 23।

ବିକଳ୍ପ ସମାଧାନ :
(i) 15 ଓ 27 ମଧ୍ଯସ୍ଥ ଗୋଟିଏ ସମାନ୍ତର ମଧ୍ୟକ = \(\frac{15+27}{2}=\frac{42}{2}=21\)
(ii) ମନେକର 15 ଓ 27 ମଧ୍ୟସ୍ଥ ଦୁଇଟି ସମାନ୍ତର ମଧ୍ଯକ x, y ।
∴ 15, x, y, 27 A.P. ରେ ଆବସ୍ଥିତ ।
a = 15, a + d = x, a + 2d = y, a + 3d = 27
⇒ 15 + 3d = 27 ⇒ 3d = 27 – 15 = 12 ⇒ d = 4
x = a + d = 15 + 4 = 19, y = a + 2d = 15 + 2 × 4 = 23
∴ 15 ଓ 27 ମଧ୍ୟସ୍ଥ ଦୁଇଟି ସମାନ୍ତର ମଧ୍ଯକ 19 ଏବଂ 23 ।

ବିକଳ୍ପ ପ୍ରଣାଳୀ :
ଏଠାରେ d = \(\frac{27-15}{3}=\frac{12}{3}=4\)
x₁ = a + d = 15 + 4 = 19 ଏବଂ x₂ = a + 2d = 15 + 2 × 4 = 23

Question 6.
12 ଓ 36 ମଧ୍ଯରେ (i) ଦୁଇଗୋଟି ଓ (ii) ତିନିଗୋଟି ସମାନ୍ତର ମଧ୍ଯକ ସ୍ଥାପନ କର ।
ସମାଧାନ :
(i) ମନେକର 12 ଓ 36 ମଧ୍ଯରେ ଅବସ୍ଥିତ ଦୁଇଟି ସମାନ୍ତର ମଧ୍ଯକ p₁ ଓ p₂।
ଏଠାରେ a = 12, b = 36, d = \(\frac{b-a}{3}=\frac{36-12}{3}=\frac{24}{3}=8\)
P₁ = a + d = 12 + 8 = 20, p₂ = 12 + 2d = 12 + 2 × 8 = 28
∴ 12 ଓ 36 ମଧ୍ୟରେ ଅବସ୍ଥିତ ଦୁଇଟି ସମାନ୍ତର ମଧ୍ଯକ 20 ଓ 28 ।

(ii) ମନେକର 12 ଓ 36 ମଧ୍ଯରେ ଅବସ୍ଥିତ ଦୁଇଟି ସମାନ୍ତର ମଧ୍ଯକ x₁,x₂ ଓ x₃।
ଏଠାରେ a = 12, b = 36, d = \(\frac{b-a}{4}=\frac{36-12}{4}=\frac{24}{4}=6\)
x₁ = a + d = 12 + 6 = 18, x₂ = a + 2d = 12 + 2 × 6 = 24.
x₃ = a + 3d = 12 + 3 × 6 = 12 + 18 = 30
∴ 12 ଓ 36 ମଧ୍ୟରେ ଅବସ୍ଥିତ ଦୁଇଟି ସମାନ୍ତର ମଧ୍ଯକ 18, 24 ଓ 30 ।

ବିକଳ୍ପ ସମାଧାନ :
(i) ମନେକର 12 ଓ 36 ମଧ୍ଯସ୍ଥ ଗୋଟି ସମାନ୍ତର ମଧ୍ୟକ x ଏବଂ y ।
∴ 12, x, y, 36 A.P. ରେ ଆସ୍ଥିତ ।
ଏଠାରେ a = 12 ଓ t₄ = 36 ⇒ a + (4 – 1) d = 36
⇒ 12 + 3d = 36 ⇒ 3d = 36 – 12 = 24 ⇒ d = \(\frac{24}{3}=8\)
x = a + d = 12 + 8 = 20, y = a + 2d = 12 + 2 × 8 = 28

(ii) ମନେକର 12 ଓ 36 ମଧ୍ୟସ୍ଥ ଦୁଇଟି ସମାନ୍ତର ମଧ୍ଯକ x, y, z । 12, x, y, z, 36 A.P. ରେ ଆସ୍ଥିତ ।
ଏଠାରେ a = 12 ଓ t₅ = 36 ⇒ a + (5 – 1) d = 36
⇒ a + 4d = 36 ⇒ 4d = 36 – 12 = 24 ⇒ d = 6
x = a + d = 12 + 6 = 18, y = a + 2d = 12 + 2 × 6 = 12 + 12 = 24
z = a + 23d = 12 + 3 × 6 = 12 + 18 = 30

Question 7.
6 ଓ 46 ମଧ୍ଯରେ (i) ଦୁଇଗୋଟି ଓ (ii) ତିନିଗୋଟି ସମାନ୍ତର ମଧ୍ଯକ ସ୍ଥାପନ କର ।
ସମାଧାନ :
(i) ମନେକର 6 ଓ 46 ମଧ୍ୟରେ ଅବସ୍ଥିତ ଦୁଇଟି ସମାନ୍ତର ମଧ୍ୟକ x₁ ଓ x₂।
ଏଠାରେ a = 6, b = 46, d = \(\frac{46-6}{3}=\frac{40}{3}\)
x₁ = a + d = 6 + \(\frac{40}{3}\) = \(\frac{18+40}{3}=\frac{58}{3}\)
x₂ = a + 2d = 6 + 2 × \(\frac{40}{3}\) = \(6+\frac{80}{3}=\frac{18+80}{3}=\frac{98}{3}\)
∴ 6 ଓ 46 ମଧ୍ୟରେ ଦୁଇଟି ସମାନ୍ତର ମଧ୍ୟକ \(\frac{58}{3}\) ଓ \(\frac{58}{3}\) ।

(ii) ମନେକର 6 ଓ 46 ମଧ୍ୟରେ 4ଟି ସମାନ୍ତର ମଧ୍ୟକ x₁,x₂,x₃ ଓ x₄।
ଏଠାରେ a = 6, b = 46,
d = \(\frac{b-a}{5}=\frac{46-6}{5}=\frac{40}{5}=8\)
x₁ = a + d = 6 + 8 = 14
x₂ = a + 2d = 6 + 2 × 8 = 22
x₃ = a + 3d = 6 + 3 × 8 = 30
x₄ = a + 4d = 6 + 4 × 8 = 38
∴ 6 ଓ 46 ମଧ୍ୟସ୍ଥ ଚାରିଗୋଟି ସମାନ୍ତର ମଧ୍ୟକ 14, 22, 30 ଓ 38 ।

Question 8.
5 ଓ 65 ମଧ୍ଯରେ (i) ତିନିଗୋଟି ଓ (ii) ପାଞ୍ଚଗୋଟି ସମାନ୍ତର ମଧ୍ଯକ ସ୍ଥାପନ କର ।
ସମାଧାନ :
(i) ମନେକର 5 ଓ 65 ମଧ୍ୟରେ ଅବସ୍ଥିତ ତିନିଗୋଟି ସମାନ୍ତର ମଧ୍ୟକ x₁, x₂ ଓ x₃ ।
ଏଠାରେ a = 5, b = 65
d = \(\frac{b-a}{4}=\frac{65-5}{4}=\frac{60}{5}=15\)
x₁ = a + d = 5 + 15 = 20
x₂ = a + 2d = 5 + 2 × 15 = 35
x₃ = a + 3d = 5 + 3 × 15 = 50
∴ 5 ଓ 65 ମଧ୍ଯସ୍ଥ ତିନୋଟି ସମାନ୍ତର ମଧ୍ଯକ 20, 35, 50 ।

(ii) ମନେକର 5 ଓ 65 ମଧ୍ୟସ୍ଥ ପାଞ୍ଚାଗୋଟି ସମାନ୍ତର ମଧ୍ୟକ x₁, x₂, x₃, x₄ ଓ x₅ ।
ଏଠାରେ a = 5, b = 65
d = \(\frac{b-a}{6}=\frac{65-5}{6}=\frac{60}{6}=10\)
x₁ = a + d = 5 + 10 = 15
x₂ = a + 2d = 5 + 2 × 10 = 25
x₃ = a + 3d = 5 + 3 × 10 = 35
x₄ = a + 2d = 5 + 4 × 10 = 45
x₅ = a + 3d = 5 + 5 × 10 = 55
∴ 5 ଓ 65 ମଧ୍ଯସ୍ଥ ପାଞ୍ଚଗୋଟି ସମାନ୍ତର ମଧ୍ଯକ 15, 25, 35, 45 ଓ 55 ।

Question 9.
11 ଓ 71 ମଧ୍ୟରେ ପାଞ୍ଚଗୋଟି ସମାନ୍ତର ମଧ୍ଯକ ସ୍ଥାପନ କର ।
ସମାଧାନ :
ମନେକର 11 ଓ 71 ମଧ୍ୟସ୍ଥ ପାଞ୍ଚଗୋଟି ସମାନ୍ତର ମଧ୍ଯକ x₁, x₂, x₃, x₄ ଓ x₅ ।
ଏଠାରେ a = : 11, b = 71, d = \(\frac{b-a}{6}=\frac{71-11}{6}=\frac{60}{6}=10\)
x₁ = a + d = 11 + 10 = 21
x₂ = a + 2d = 11 + 2 × 10 = 31
x₃ = a + 3d = 11 + 3 × 10 = 41
x₄ = a + 2d = 11 + 4 × 10 = 51
x₅ = a + 3d = 11 + 5 × 10 = 11 + 50 = 61
∴ 11 ଓ 71 ମଧ୍ୟସ୍ଥ ପାଞ୍ଚଗୋଟି ସମାନ୍ତର ମଧ୍ୟକ 21, 31, 41, 51 ଓ 61 ।

ବିକଳ୍ପ ସମାଧାନ :
ମନେକର 11 ଓ 71 ମଧ୍ୟସ୍ଥ ପାଞ୍ଚଟି ସମାନ୍ତର ମଧ୍ଯକ p, q, r, s ଓ t ।
∴ 11, p, g, r, s, t, 71 A.P.ରେ ଅବସ୍ଥିତ ।
ଏଠାରେ a = 11, t, = 71
t₇ = 71 ⇒ a + (7 – 1)= 71 ⇒ 11 + 6d = 71
⇒ 6d = 71 – 11 = 60 ⇒ d = \(\frac{60}{6}=10\)
p = a + d = 11 + 10 = 21
q = a + 2d = 11 + 2 × 10 = 31
r = a + 3d = 11 + 3 × 10 = 41
s = a + 4d = 11 + 4 × 10 = 51
t = a + 5d = 11 + 5 × 10 = 61
∴ 11 ଓ 71 ମଧ୍ୟସ୍ଥ ପାଞ୍ଚଟି ସମାନ୍ତର ମଧ୍ୟକ 21, 31, 41, 51 ଓ 61 ।

Question 10.
20 ଓ 80 ମଧ୍ୟରେ n ସଂଖ୍ୟକ A.M. ଅଛି । ଯଦି ପ୍ରଥମ ମଧ୍ୟକ : ଶେଷ ମଧ୍ଯକ = 1 : 3 ହୁଏ ତେବେ, nର ମାନ ସ୍ଥିର କର ।
ସମାଧାନ :
20 ଓ 80 ମଧ୍ୟରେ n ସଂଖ୍ୟକ A.M. ଅଛି । ଏଠାରେ a = 20
t_n+2 = 80 ⇒ a + (n + 2 – 1) d = 80
⇒ 20 + (n+1)d = 80 ⇒ (n + 1) d = 80 – 20 ⇒ (n + 1) d = 60 …….(i)
ପ୍ରଥମ ମଧ୍ୟକ = 20 + d ଓ ଶେଷ ମଧ୍ଯକ = 80 – d
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{20+d}{80-d}=\frac{1}{3}\) ⇒ 60 + 3d = 80 – d ⇒ 80 – 60 = 20 ⇒ d = 5
∴ (i)ରୁ (n + 1) d = 60 ⇒ (n + 1) 5 = 60
⇒ n + 1 = \(\frac{60}{5}\) = 12 ⇒ n = 12 -1 = 11
∴ nର ମାନ 11 ଅଟେ ।

Question 11.
A.P.ରେ ଥିବା ଚାରିଗୋଟି ସଂଖ୍ୟା ନିର୍ଣ୍ଣୟ କର ଯାହାର ଯୋଗଫଳ 2 ଏବଂ ଆଦ୍ୟ ଓ ପ୍ରାନ୍ତ ରାଶିଦ୍ଧୟର ଗୁଣଫଳ ମଧ୍ଯକ ଦ୍ଵୟର ଗୁଣଫଳର 10 ଗୁଣ ସହ ସମାନ ହେବ ।
ସମାଧାନ :
ମନେକର A.P. ରେ ଥ‌ିବା ଚାରୋଟି ସଂଖ୍ୟା ଯଥାକ୍ରମେ a – 3d, a – d, a + d, a + 3d ।
ପ୍ରଶ୍ନନୁସାରେ, a – 3d + a – d + a + d + a + 3d = 2
⇒ 4a = 2 ⇒ a = \(\frac{2}{4}=\frac{1}{2}\)
ପୁନଶ୍ଚ, (a – 3d) (a + 3d) = 10 (a – d) (a + d)
⇒ a² – 9d² = 10(a² – d²) ⇒ 10a² – 10d² = a² – 9d²
⇒ 10a² – a² = 10² – 9d² ⇒ 9a² = d²
⇒ 9 × (\(\frac{1}{2}\))² = d² = \(\frac{9}{4}\) = d = ±\(\sqrt{\frac{9}{4}}\)
d = ±\(\frac{3}{2}\)
a = \(\frac{1}{2}\) ଓ d = \(\frac{3}{2}\) ହେଲେ
a – 3d = \(\frac{1}{2}\) – 3 × \(\frac{3}{2}\) = \(\frac{1}{2}-\frac{9}{2}=\frac{-8}{2}=-4\)
a – d = \(\frac{1}{2}\) – \(\frac{3}{2}\) = \(\frac{-2}{2}\) = -1
a + d = \(\frac{1}{2}\) + \(\frac{3}{2}\) = \(\frac{4}{2}\) = 2
a + 3d = \(\frac{1}{2}\) + 3 × \(\frac{3}{2}\) = \(\frac{10}{2}\) = 5
a = \(\frac{1}{2}\) ଓ d = \(\frac{-3}{2}\) ହେଲେ A.P. ଚାରୋଟି ପଦ 5, 2, – 1, – 4 ହେବ ।
∴ A.P.ରେ ଥ‌ିବା ଚାରୋଟି ସଂଖ୍ୟା ଯଥାକ୍ରମେ -4, -1, 2, 5 ବା 5, 2, -1, -4 ।