BSE Odisha 10th Class Maths Solutions Algebra Chapter 5 ପରିସଂଖ୍ୟାନ Ex 5(a)

Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 5 ପରିସଂଖ୍ୟାନ Ex 5(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Algebra Chapter 5 ପରିସଂଖ୍ୟାନ Ex 5(a)

(କ – ବିଭାଗ )

Question 1.
ନିମ୍ନ ଉକ୍ତିମାନଙ୍କ ମଧ୍ୟରୁ ଯେଉଁଟି ଠିକ୍ ତା’ ପାଖରେ T ଓ ଯେଉଁଟି ଭୁଲ ତା’ ପାଖରେ F ଲେଖ ।
(i) ଦୁଇଟି କ୍ରମିକ ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ମାଧ୍ୟମାନ ସେ ଦ୍ଵୟ ମଧ୍ୟବର୍ତ୍ତୀ ଯୁଗ୍ମସଂଖ୍ୟା ସଙ୍ଗେ ସମାନ ।
(ii) ଏକ ସମାନ୍ତର ପ୍ରଗତିରେ ଥିବା ତିନୋଟି କ୍ରମିକ ପଦର ମାଧ୍ଯମାନ ସେମାନଙ୍କର ମଧ୍ଯମପଦ ସଙ୍ଗେ ସମାନ ।
(iv) ଭିନ୍ନ ଭିନ୍ନ ଆରମ୍ଭ ବିନ୍ଦୁ ନେଇ ଦତ୍ତ ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ ନିର୍ଣ୍ଣୟ କଲେ ଭିନ୍ନ ଭିନ୍ନ ଉତ୍ତର ମିଳିବ ।
(v) କୌଣସି ତଥ୍ୟାବଳୀର ଆରମ୍ଭ ବିନ୍ଦୁ 20 ହେଲେ ଅନ୍ତର୍ଭୁକ୍ତ ଲବ୍‌ଧାଙ୍କ 15ର ବିଚ୍ୟୁତି 5 ।
(vi) ପ୍ରଥମ n ସଂଖ୍ୟକ ଗଣନ ସଂଖ୍ୟାର ମାଧ୍ୟମାନ \(\frac{n+2}{2}\)।
(vii) ପ୍ରଥମ n ସଂଖ୍ୟକ ଯୁଗ୍ମ ସଂଖ୍ୟାର ମାଧ୍ୟମାନ 2n + 2 ।
(viii) ପ୍ରଥମ ଦଶଗୋଟି ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ମାଧ୍ୟମାନ 10 ।
(ix) 15 ଗୋଟି ସଂଖ୍ୟାର ମାଧ୍ୟମାନ 17 । ପ୍ରତ୍ୟେକ ସଂଖ୍ୟାକୁ 2 ଦ୍ୱାରା ଗୁଣି ସେମାନଙ୍କର ମାଧ୍ଯମାନ ସ୍ଥିର କଲେ ମାଧ୍ୟମାନ 8.5 ହେବ ।
(x) ପ୍ରଥମ 20ଟି ଯୁଗ୍ମ ଗଣନ ସଂଖ୍ୟାର ମାଧ୍ୟମାନ, ପ୍ରଥମ 20ଟି ଗଣନ ସଂଖ୍ୟାର ମାଧମାନର ଦୁଇ ଗୁଣ ।
ଉ :
(i) ଦୁଇଟି କ୍ରମିକ ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ମାଧ୍ୟମାନ ସେ ଦ୍ଵୟ ମଧ୍ୟବର୍ତ୍ତୀ ଯୁଗ୍ମସଂଖ୍ୟା ସଙ୍ଗେ ସମାନ । (T)
(ii) ଏକ ସମାନ୍ତର ପ୍ରଗତିରେ ଥିବା ତିନୋଟି କ୍ରମିକ ପଦର ମାଧ୍ଯମାନ ସେମାନଙ୍କର ମଧ୍ଯମପଦ ସଙ୍ଗେ ସମାନ । (T)
(iv) ଭିନ୍ନ ଭିନ୍ନ ଆରମ୍ଭ ବିନ୍ଦୁ ନେଇ ଦତ୍ତ ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ ନିର୍ଣ୍ଣୟ କଲେ ଭିନ୍ନ ଭିନ୍ନ ଉତ୍ତର ମିଳିବ । (T)
(v) କୌଣସି ତଥ୍ୟାବଳୀର ଆରମ୍ଭ ବିନ୍ଦୁ 20 ହେଲେ ଅନ୍ତର୍ଭୁକ୍ତ ଲବ୍‌ଧାଙ୍କ 15ର ବିଚ୍ୟୁତି 5 । (F)
(vi) ପ୍ରଥମ n ସଂଖ୍ୟକ ଗଣନ ସଂଖ୍ୟାର ମାଧ୍ୟମାନ \(\frac{n+1}{2}\)। (T)
(vii) ପ୍ରଥମ n ସଂଖ୍ୟକ ଯୁଗ୍ମ ସଂଖ୍ୟାର ମାଧ୍ୟମାନ 2n + 2 । (F)
(viii) ପ୍ରଥମ ଦଶଗୋଟି ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ମାଧ୍ୟମାନ 10 । (T)
(ix) 15 ଗୋଟି ସଂଖ୍ୟାର ମାଧ୍ୟମାନ 17 । ପ୍ରତ୍ୟେକ ସଂଖ୍ୟାକୁ 2 ଦ୍ୱାରା ଗୁଣି ସେମାନଙ୍କର ମାଧ୍ଯମାନ ସ୍ଥିର କଲେ ମାଧ୍ୟମାନ 8.5 ହେବ । (F)
(x) ପ୍ରଥମ 20ଟି ଯୁଗ୍ମ ଗଣନ ସଂଖ୍ୟାର ମାଧ୍ୟମାନ, ପ୍ରଥମ 20ଟି ଗଣନ ସଂଖ୍ୟାର ମାଧମାନର ଦୁଇ ଗୁଣ । (F)

ବ୍ୟାଖ୍ୟା ସହ ଉତ୍ତର:
(i) (T) (କାରଣ 3 ଓ 5ର ମାଧ୍ୟମାନ \(\frac{3+5}{2}=4\))
(ii) (T) (କାରଣ AM \(\frac{a+b}{2}\))
(iii) (T) (କାରଣ ମାଧ୍ଯମାନର ପ୍ରତିଶବ୍ଦ ହାରାହାରି ଅଟେ ।)
(iv) (F) (ସର୍ବଦା ବିଚ୍ୟୁତିର ମାଧ୍ଯମାନ ସହିତ ଆରମ୍ଭ ବିନ୍ଦୁ ଯୋଗ କରାଯାଏ, ତେଣୁ ଉତ୍ତର ସର୍ବଦା ସମାନ ହେବ ।)
(v) (F) (କାରଣ ବିଚ୍ୟୁତି = ଲବ୍‌ଧାଙ୍କ – ଆରମ୍ଭ ବିନ୍ଦୁ = 15 – 20 = – 5)
(vi) (T) (କାରଣ ପ୍ରଥମ n ସଂଖ୍ୟକ ସଂଖ୍ୟାର ସମଷ୍ଟି = \(\frac{n(n+1)}{2}\)
∴ ମାଧ୍ୟମାନ = \(\frac{n(n+1)}{2n}=\frac{n+1}{2}\))
(vii) (F) (ସୂତ୍ର ଅନୁସାରେ n + 1 ହେବ ।)
(viii) (T) (କାରଣ ପ୍ରଥମ ଦଶଟି ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ସମଷ୍ଟି = 10², ମାଧ୍ୟମାନ = \(\frac{10²}{10}\) = 10)
(ix) (F) (କାରଣ ମାଧମାନ 2 ଗୁଣ ହେବ ।)
(x) (F) (କାରଣ, ପ୍ରତ୍ୟେକ ସଂଖ୍ୟାରେ 2 ଗୁଣିଲେ ତା 20ଟି ଯୁଗ୍ମ ଗଣନ ସଂଖ୍ୟା ହେବ ।)

Question 2.
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନ ପାଇଁ ପ୍ରଦତ୍ତ ସମ୍ଭାବ୍ୟ ଉତ୍ତରମାନଙ୍କ ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛ ।
(i) 61, 62, 68, 56, 64, 72, 69, 51, 71, 67, 70, 55, 63 ଏହି ଲବ୍ଧାଙ୍କମାନଙ୍କର ମାଧ୍ୟମାନ ନିରୂପଣ ଲାଗି ନିମ୍ନସ୍ଥ ସଂଖ୍ୟାମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁଟି ଉପଯୁକ୍ତ ଆରମ୍ଭ ବିନ୍ଦୁ ହେବ ?
(A) 55
(B) 60
(C) 70
(D) 72

(ii) ପ୍ରଥମ 20ଟି ଗଣନ ସଂଖ୍ୟାର ମାଧ୍ୟମାନ କେତେ ?
(A) 10
(B) 10½
(C) \(\frac{21}{20}\)
(D) 210

(iii) ପ୍ରଥମ ‘n’ ସଂଖ୍ୟକ ସଂପ୍ରସାରିତ ସ୍ଵାଭାବିକ ସଂଖ୍ୟା (Whole number)ର ମାଧ୍ଯମାନ କେତେ ?
(A) \(\frac{n-1)}{2}\)
(B) \(\frac{n}{2}\)
(C) \(\frac{n+1}{2}\)
(D) n

(iv) ପ୍ରଥମ ‘n’ ସଂଖ୍ୟକ ଯୁଗ୍ମ ସଂଖ୍ୟାର ମାଧ୍ଯମାନ କେତେ ?
(A) (n – 1)
(B) n
(C) n + 1
(D) n + 2

(v) ପ୍ରଥମ n ସଂଖ୍ୟକ ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ମାଧ୍ଯମାନ କେତେ ?
(A) (n – 11)
(B) n
(C) n + 1
(D) n + 2

(vi) ‘m’ ମାଧମାନ ବିଶିଷ୍ଟ 10ଟି ଲବ୍‌ଧାଙ୍କ ମଧ୍ୟରୁ ପ୍ରତ୍ୟେକକୁ 2 ବଢ଼ାଇଲେ ନୂତନ ଲବ୍‌ଧାଙ୍କ 10ଟିର ମାଧ୍ଯମାନ କେତେ ହେବ ?
(A) (n – 11)
(B) n
(C) n + 1
(D) n + 2

(vii) ‘M’ ମାଧ୍ୟମାନ ବିଶିଷ୍ଟ n ସଂଖ୍ୟକ ଲବ୍‌ଧାଙ୍କମାନଙ୍କ ମଧ୍ୟରୁ ପ୍ରତ୍ୟେକକୁ 4 ଗୁଣ କରିଦେଲେ ନୂତନ ଲବ୍‌ଧାଙ୍କମାନଙ୍କର ମାଧ୍ଯମାନ କେତେ ହେବ ?
(A) \(\frac{M)}{4}\)
(B) M
(C) 4M
(D) \(\frac{4}{M}\)

(viii) ‘M’ ମାଧ୍ଯମାନ ବିଶିଷ୍ଟ n ସଂଖ୍ୟକ ଲବ୍‌ଧାଙ୍କମାନଙ୍କ ମଧ୍ୟରୁ ପ୍ରତ୍ୟେକରୁ x ବିୟୋଗ କଲେ ନୂତନ ଲବ୍‌ଧାଙ୍କମାନଙ୍କର ମାଧ୍ଯମାନ କେତେ ହେବ ?
(A) M
(B) (M + x)
(C) Mx
(D) (M – x)

(ix) ‘M’ ମାଧ୍ଯମାନ ବିଶିଷ୍ଟ n ସଂଖ୍ୟକ ଲବ୍‌ଧାଙ୍କମାନଙ୍କ ମଧ୍ୟରୁ ପ୍ରତ୍ୟେକକୁ 5 ଦ୍ଵାରା ଭାଗକଲେ ନୂତନ ଲବ୍‌ଧାଙ୍କମାନଙ୍କର ମାଧ୍ଯମାନ କେତେ ହେବ ?
(A) M
(B) \(\frac{M}{5}\)
(C) 5M
(D) M – 5

(x) ଯଦି à ସଂଖ୍ୟକ ବାଳକମାନଙ୍କର ମାଧ୍ଯମାନ ବୟସ 12 ବର୍ଷ ଓ b ସଂଖ୍ୟକ ବାଳିକାଙ୍କର ମାଧ୍ଯମାନ ବୟସ 10 ବର୍ଷ ହୁଏ, ତେବେ ଉପରୋକ୍ତ ସମସ୍ତ ବାଳକ ବାଳିକାଙ୍କର ମାଧ୍ଯମାନ ବୟସ କେତେ ବର୍ଷ ହେବ ?
(A) \(\frac{10a+12b}{a+b}\)
(B) \(\frac{12a+10b}{a+b}\)
(C) \(\frac{10a+12b}{10+12}\)
(D) \(\frac{12a+10b}{10+12}\)

(xi) 998.9, 999.1, 1000-3, 1000-6, 1000.1 ର ମାଧ୍ୟମାନ କେତେ?
(A) 998
(B) 999
(C) 1000
(D) 1001

(xii) 6,8, 5, 7, x ଏବଂ 4 ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକର ମାଧ୍ଯମାନ 7 ହେଲେ xର ମାନ କେତେ ହେବ ?
(A) 10
(B) 11
(C) 12
(D) 13

(xiii) E₁, E₂, E₃, E₄, E₅, E₆ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକର ମାଧ୍ଯମାନ M ହେଲେ ⁶Σ_i=1(x₁ – M)ର ମାନ କେତେ ହେବ ?
(A) 0
(B) 6
(C) 36
(D) -6

(xiv) x, x + 2, x + 4, x + 6, x + 8ର ମାଧ୍ୟମାନ କେତେ ?
(A) x+2
(B) x + 4
(C) x+6
(D) x

(xv) 18ର ସମସ୍ତ୍ର ଗୁଣନୀୟକମାନଙ୍କର ମାଧ୍ୟମାନ କେତେ
(A) 5
(B) 6
(C) 6.5
(D) 7

ଉତ୍ତର:
(i) 69
(ii) 10½
(iii) \(\frac{n-1}{2}\)
(iv) n + 1
(v) n
(vi) m + 2
(vii) 4M
(viii) (M – x)
(ix) \(\frac{M}{5}\)
(x) \(\frac{12a+10b}{a+b}\)
(xi) 1000
(xi) 1000
(xii) 12
(xiii) 0
(xiv) x + 4
(xv) 6.5

(ଖ – ବିଭାଗ )

Question 3.
ଦଶଥର ଖେଳି ଜଣେ କ୍ରିକେଟ୍ ଖେଳାଳୀ ସଂଗ୍ରହ କରିଥିବା ରଗୁଡ଼ିକ ହେଲା – 47, 41, 50, 39, 45, 48,
42, 32, 60 ଏବଂ 20 । ତାଙ୍କଦ୍ୱାରା ସଂଗୃହୀତ ରନ୍‌ର ମାଧ୍ଯମାନ ସଂକ୍ଷିପ୍ତ ପ୍ରଣାଳୀରେ (ଉପଯୁକ୍ତ ଆରମ୍ଭ ବିନ୍ଦୁ ନେଇ) ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ମନେକର ଆରମ୍ଭ ବିନ୍ଦୁ 45 1 ( ∵ ସର୍ବନିମ୍ନ ଏବଂ ସର୍ବାଧ‌ିକ ରନ୍ ଯଥାକ୍ରମେ 20 ଏବଂ 60) ।
∴ ଲବ୍ଧାଙ୍କମାନଙ୍କର ବିଚ୍ୟୁତିମାନ 2, − 4, 5, 6, 0, 3, – 3, −13, 15, – 25
ବିଚ୍ୟୁତିମାନଙ୍କର ସମଷ୍ଟି = – 26

∴ ଦଶଥର ଖେଳି ସଂଗୃହୀତ ରନ୍‌ର ମାଧ୍ୟମାନ = 42.4

Question 4.
କିଲୋଗ୍ରାମ୍ ଓଜନରେ 30 ଜଣ ପିଲାଙ୍କର ଓଜନ ହେଲା 21, 30, 40, 25, 26, 22, 26, 31, 22, 36, 30, 25, 25, 33, 30, 25, 27, 27, 25, 31, 33, 22, 21, 36, 40, 31, 33, 30, 37, 36 | ଏହି ତଥ୍ୟାବଳୀକୁ ବାରମ୍ବାରତା ବଣ୍ଟନରେ ସଜ୍ଜିତ କରି ମାଧ୍ଯମାନ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ଓଜନ କିଲୋଗ୍ରାମ୍ ମାପରେ ଥ‌ିବା ଲବ୍‌ଧାଙ୍କମାନଙ୍କୁ ବାରମ୍ବାରତା ବଣ୍ଟନ ସାରଣୀରେ ରଖିଲେ –

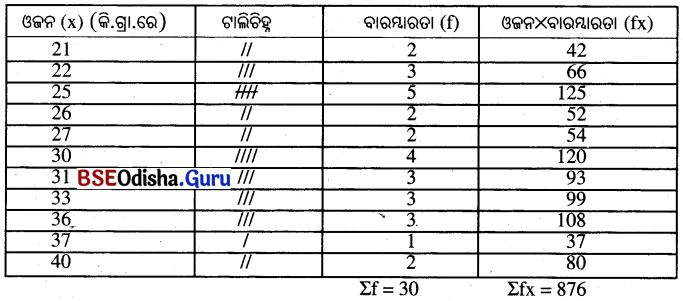
ଉକ୍ତ ସାରଣୀରୁ 2f = 30 ଏବଂ Efx = 876.. ମାଧ୍ୟମାନ = \(\frac{Σf_x}{Σf}\)

Question 5.
କିଛି ରାସାୟନିକ ପଦାର୍ଥର ଓଜନ 30 ଥର ନିଆଯାଇ ଫଳାଫଳକୁ ନିମ୍ନ ସାରଣୀରେ ସଜାଯାଇଛି । ମାଧ୍ଯମାନ ଓଜନ ନିର୍ଣ୍ଣୟ କର ।

ଓଜନ (ଗ୍ରାମ୍‌ରେ)	3.8	3.9	4.0	4.1	4.2	4.3	4.4	4.5	4.6
ବାରମ୍ବାରତା	1	1	6	6	7	5	2	1	1

ସମାଧାନ :

ଓଜନ (ଗ୍ରାମ୍‌ରେ) (x)	ବାରମ୍ବାରତା (f)	ଓଜନ × ବାରମ୍ବାରତା (fx)
3.8	1	3.8
3.9	1	3.9
4.0	6	24.0
4.1	6	24.6
4.2	7	29.4
4.3	5	21.5
4.4	2	8.8
4.5	1	4.5
4.6	1	4.6
	Σf=30	Σfx=125.1

∴ ମାଧ୍ଯମାନ = \(\frac{Σf_x}{Σf}=\frac{125.1}{30}=4.17\)
∴ ମାଧ୍ୟମାନ ଓଜନ 4.17 ଗ୍ରାମ୍ ।

Question 6.
ଏକ ଶ୍ରେଣୀରେ 30 ଜଣ ଛାତ୍ରଙ୍କର ହାରାହାରି ବୟସ 12 ବର୍ଷ । ଶ୍ରେଣୀ ଶିକ୍ଷକଙ୍କ ସହିତ ସେମାନଙ୍କର ହାରାହାରି ବୟସ 13 ବର୍ଷ ହେଲେ, ଶ୍ରେଣୀ ଶିକ୍ଷକଙ୍କ ବୟସ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ଏକ ଶ୍ରେଣୀରେ 30 ଜଣ ଛାତ୍ରଙ୍କର ହାରାହାରି ବୟସ 12 ବର୍ଷ ।
30 ଜଣ ଛାତ୍ରଙ୍କର ମୋଟ ବୟସ = 30 × 12 = 360 ବର୍ଷ ।
ଛାତ୍ରମାନଙ୍କ ସହ ତାଙ୍କର ଶ୍ରେଣୀଶିକ୍ଷକ ମିଶିବାରୁ ହାରାହାରି ବୟସ 13 ବର୍ଷ ହେଲା ।
∴ 31 ଜଣ ଅର୍ଥାତ୍ 30 ଜଣ ଛାତ୍ର ଓ ଜଣେ ଶ୍ରେଣୀ ଶିକ୍ଷକଙ୍କ ମୋଟ ବୟସ = 31 × 13 = 403 ବର୍ଷ ।
ଶ୍ରେଣୀ ଶିକ୍ଷକଙ୍କ ବୟସ = 403 – 360 = 43 ବର୍ଷ ।
∴ ଶ୍ରେଣୀ ଶିକ୍ଷକଙ୍କ ବୟସ 43 ବର୍ଷ ।

Question 7.
x₁, x₂, x₃ …… ପ୍ରଭୃତି n ସଂଖ୍ୟକ ଲବ୍‌ଧାଙ୍କର ମାଧ୍ଯମାନ m । ଯଦି ପ୍ରତ୍ୟେକ ଲବ୍‌ଧାଙ୍କରେ (a + b) ଯୋଗ କରାଯାଏ ଦର୍ଶାଅ ଯେ, ନୂତନ ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକର ମାଧମାନ (m + a + b) ହେବ ।
ସମାଧାନ :
ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକ ହେଲେ x₁, x₂, x₃ ……… x_n
ଉକ୍ତ n-ସଂଖ୍ୟକ ଲବ୍‌ଧାଙ୍କମାନଙ୍କର ମାଧ୍ଯମାନ (m) = \(\frac{x_1+x_2+x_3+…..x_n}{n}\)

(ଗ – ବିଭାଗ )

Question 8.

ସମାଧାନ :

ଉଚ୍ଚତା (x)	ବାରମ୍ବାରତା (f)	ଫଭାଗର ମଧ୍ୟବିନ୍ଦୁ	ମଧ୍ୟବିନ୍ଦୁ × ବାରମ୍ବାରତା (fy)
70-65	4	67.5	270.0
65-60	7	62.5	437.5
60-55	8	57.5	460.0
55-50	10	52.5	525.0
50-45	5	47.5	237.5
45-40	6	42.5	255.0
40-35	3	37.5	112.5
35-30	7	32.5	227.5
30-25	2	27.5	55.0
	Σf = 52		Σfy = 2580.00

∴ ମାଧ୍ଯମାନ = \(\frac{Σfy}{Σf}=\frac{2580}{52}=49.6\)
ବିକଳ୍ପ ପ୍ରଣାଳୀ : (ସଂକ୍ଷିପ୍ତ ପ୍ରଣାଳୀ)

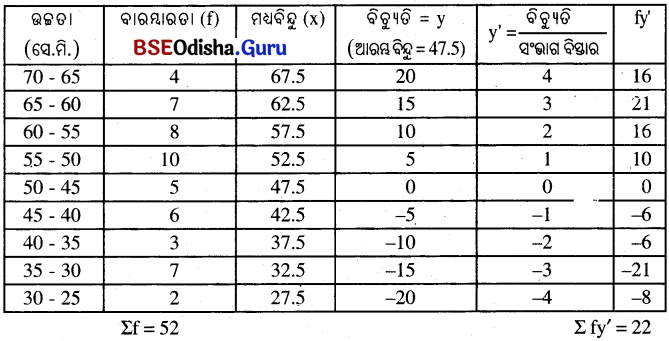
ଆରମ୍ଭ ବିନ୍ଦୁ = 47.5, ସଂଭାଗ ବିସ୍ତାର (i) = 5
ମାଧ୍ୟମାନ = ଆରମ୍ଭ ବିନ୍ଦୁ + \(\frac{Σfy’}{Σf}\) × i = 47.5 + \(\frac{22×5}{52}\) (y’ = ବିଚ୍ୟୁତି) = 47.5 + \(\frac{110}{52}\) = 47.5+2.1 = 49.6
ମଧ୍ୟବିନ୍ଦୁ = \(\frac{\text { ସଂଭାଗର ନିମ୍ନସୀମା + ସଂଭାଗର ଉଚ୍ଚସୀମା }}{2}\)
ଅନ୍ତର୍ଭୁକ୍ତ ସଂଭାଗୀକରଣରେ ସଂଭାଗ ବିସ୍ତାର = ସଂଭାଗର ଉଚ୍ଚସୀମା – ସଂଭାଗର ନିମ୍ନସୀମା

Question 9.
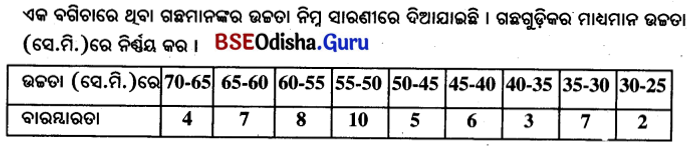
ସଂକ୍ଷିପ୍ତ ପ୍ରଣାଳୀର ନିମ୍ନ ସାରଣୀ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ ନିରୂପଣ କର ।

ସଂଭାଗ	84-90	90-96	96-102	102-108	108-114	114-120
ବାରମ୍ବାରତା	8	10	16	23	12	11

ସମାଧାନ :

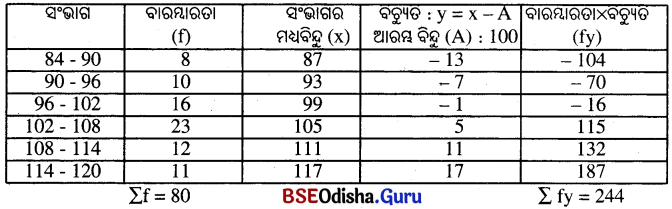
∴ ମାଧ୍ଯମାନ = A + \(\frac{Σfy}{Σf}=100+\frac{244}{80}\) = 100 + 3.05 = 103.05

Question 10.
ନିମ୍ନ ଭାଗ-ବିଭକ୍ତ ବାରମ୍ବାରତା ବିତରଣ ସାରଣୀରେ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ ସୋପାନ-ବିଦ୍ୟୁତ ପ୍ରଣାଳୀରେ ସ୍ଥିର କର ।

ସଂଭାଗ	0-4	4-8	8-12	12-16	16-20	20-24
ବାରମ୍ବାରତା	5	7	10	15	9	4

ସମାଧାନ :

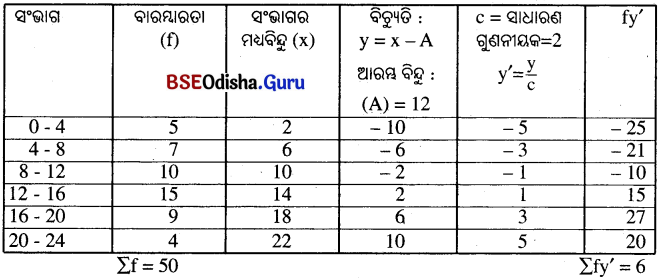
∴ ମାଧ୍ୟମାନ = ଆରମ୍ଭ ବିନ୍ଦୁ + \(\frac{Σfy’}{Σf}\) × c = 12 + \(\frac{6}{50}\) × 2 = 12 + 0.24 = 12.24
ବିକଳ୍ପ ପ୍ରଣାଳୀ : ମାଧମାନ (M) = A + \(\frac{Σfy}{Σf}\) × i
ସୂତ୍ରର ପ୍ରୟୋଗ କରି ସମାଧାନ କରାଯାଇପାରିବ । ଯେଉଁଠାରେ i = ସଂଭାଗବିସ୍ତାର ହେବ ।

Question 11.
ନିମ୍ନ ସାରଣୀରେ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ ଉଭୟ ସଂକ୍ଷିପ୍ତ ପ୍ରଣାଳୀ ଓ ସୋପାନ-ବିଦ୍ୟୁତ ପ୍ରଣାଳୀ ଅବକମୂଳରେ ସ୍ଥିର କର ।

ସଂଭାଗ (C.I.)	0-50	50-100	100-150	150-200	200-250	250-300
ବାରମ୍ବାରତା (f)	4	10	12	10	8	8

ସମାଧାନ :

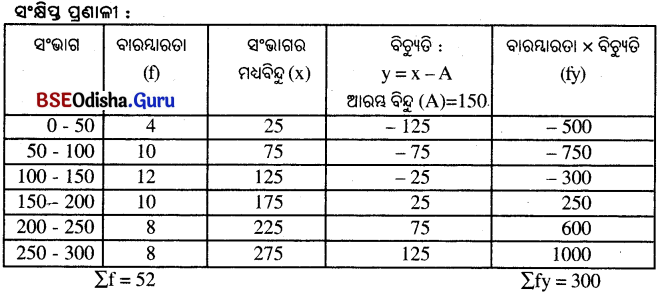
∴ ମାଧ୍ଯମାନ = A + \(\frac{Σfy}{Σf}=150+\frac{300}{52}\) = 150 + 5.77 = 155.77

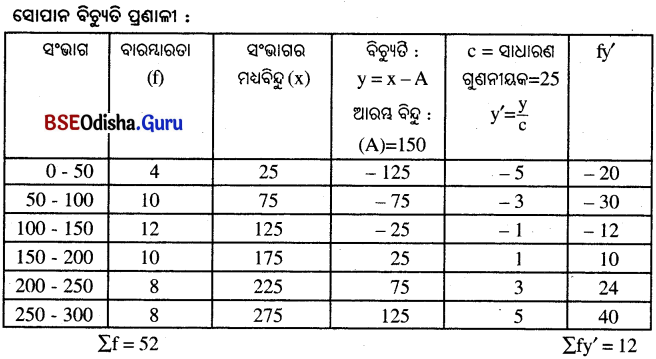
∴ ମାଧ୍ୟମାନ (M)= A + \(\frac{Σfy’}{Σf}\) × c = 150 + \(\frac{12}{52}\) × 25 = 150 + 5.77 = 155.77

Question 12.
ସୋପାନ ବିଚ୍ୟୁତି ପ୍ରଣାଳୀ ନିମ୍ନ ସାରଣୀ ଅନ୍ତର୍ଭୁକ୍ତ, ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ ସ୍ଥିର କର ।

ସଂଭାଗ	20-30	30-40	40-50	50-60	60-70	70-80
ବାରମ୍ବାରତା	10	6	8	12	5	9

ସମାଧାନ :

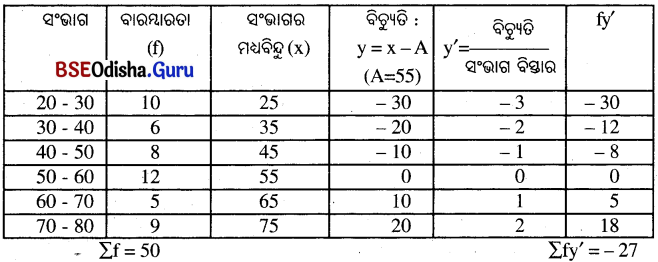
ଏଠାରେ A = 55, i = 60 – 50 = 10
∴ ମାଧ୍ୟମାନ (M)= A + \(\frac{Σfy’}{Σf}\) × i = 55 + \(\frac{-27}{50}\) × 10 = 55 + (-5.4) = 49.6

Question 13.
(i) ନିମ୍ନ ସାରଣୀ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ 7.5 ହେଲେ ‘f” ର ନିରୂପଣ କର ।

ସଂଭାଗ	5	6	7	8	9	10	11	12
ବାରମ୍ବାରତା	20	17	f	10	8	6	7	6

(ii) ମୂଲ୍ୟ ନିମ୍ନ ସାରଣୀ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ 6 ହେଲେ ‘P’ ର ମୂଲ୍ୟ ନିରୂପଣ କର ।

ସଂଭାଗ	3	6	7	4	P+3	8
ବାରମ୍ବାରତା	5	2	3	2	4	6

ସମାଧାନ :
(i) ବଡ ତଥ୍ୟାବଳୀର ମାଧ୍ୟମାନ = 7.5

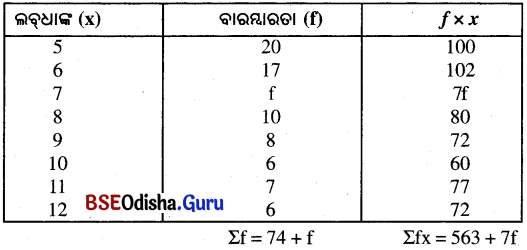
ମାଧ୍ୟମାନ (M) = \(\frac{Σfy}{Σf}\) ⇒ 7.5 = \(\frac{563+7f}{74+f}\)
⇒ 555 + 7.5f = 563 + 7f ⇒ 7.5f – 7f = 563 – 555
⇒ 0.5f = 8 ⇒ f = 8 ⇒ \(\frac{1}{2}\)f = 8 × 2 = 16

(ii) ବଡ ତଥ୍ୟାବଳୀର ମାଧ୍ୟମାନ = 6

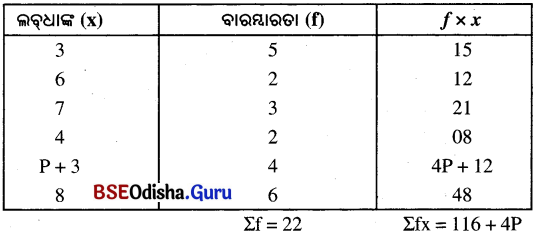
ମାଧ୍ୟମାନ (M) = \(\frac{Σfy}{Σf}\) ⇒ 6 = \(\frac{116+4p}{22}\)
⇒ 4p + 116 = 132 ⇒ 4p = 16
⇒ p = \(\frac{16}{4}\) = 4

Question 14.
ନିମ୍ନ ସାରଣୀ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀର ମାଧମାନ 50 ଏବଂ ବାରମ୍ବାରତାଗୁଡ଼ିକର ସମଷ୍ଟି 120 ହେଲେ f₁ ଓ f₂ ନିର୍ଣ୍ଣୟ କର ।

ସଂଭାଗ	0-20	20-40	40-60	60-80	80-100
ବାରମ୍ବାରତା	17	f1	32	F2	19

ସମାଧାନ :
ବଡ ସାରଣୀ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀର ମାଧମାନ = 50, ବାରମ୍ବାରତାଗୁଡ଼ିକର ସମଷ୍ଟି = 120

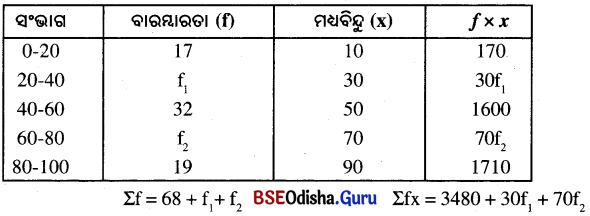
ପ୍ରଶ୍ନନୁସାରେ, 68 + f₁ + f₂ = 120
f₁ + f₂ = 52
Σfx = 3480 + 30f₁ + 70f₂ = 3480 + 30(f₁ + f₂) + 40f₂
=3480 + 30 × 52 ÷ 40f₂ = 3480+ 1560 + 40f₂ = 5040 + 40f₂
∴ ମାଧ୍ୟମାନ (m) = \(\frac{Σfx}{Σf}=\frac{5040+4f_2}{120}\)
⇒ 50= \(\frac{5040+4f_2}{120}\) ⇒ 40f₂ = 6000 – 5040 ⇒ f₂ = \(\frac{960}{40}\) = 24

ଆଗରୁ ପ୍ରମାଣିତ f₁ + f₂ =52 f₁ = 52 – 24 = 28
∴ f₁ = 28 ଏବଂ f₂ = 24

Question 15.
ସୋପାନ-ବିଚ୍ୟୁତି ପ୍ରଣାଳୀ ଅବଲମ୍ବନରେ ନିମ୍ନ ସାରଣୀ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ ସ୍ଥିର କର ।

ସଂଭାଗ	10-19	20-29	30-39	40-49	50-59	60-69	70-79
ବାରମ୍ବାରତା	5	65	222	112	53	40	3

ସମାଧାନ :

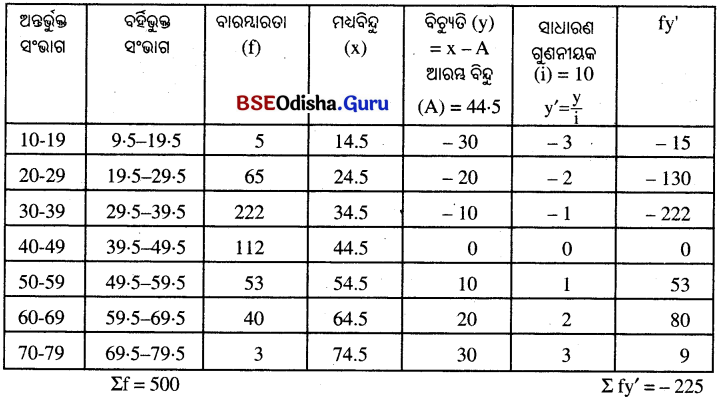
∴ ମାଧ୍ୟମାନ = A + \(\frac{Σfy’}{Σf}\) × i = 44.5 + \(\frac{-225}{500}\) × 10 = 44.5 + \(\frac{-450}{100}\) = 44.5 – 4.5 = 40

Question 16.
x₁, x₂, x₃ ……. ପ୍ରଭୃତି n ସଂଖ୍ୟକ ଲବ୍‌ଧାଙ୍କର ମାଧ୍ଯମାନ M । ଯଦି \(\sum_{i=1}^n\left(x_i-5\right)=60\) ଏବଂ \(\sum_{i=1}^n\left(x_i-8\right)\) = 24 ହୁଏ ତେବେ ‘n’ ଓ M ସ୍ଥିର କର ।
ସମାଧାନ :
x₁, x₂, x₃ ………. ପ୍ରଭୃତି n ସଂଖ୍ୟକ ଲବ୍‌ଧାଙ୍କର ମାଧମାନ M ।
⇒ \(\frac{x_1+x_2+x_3+…..x_n}{n}=M\)
⇒ x₁ + x₂ + x₃ ……. + x_n = nM
\(\sum_{i=1}^n\left(x_i-5\right)=60\)
⇒ (x₁ – 5) + (x₂ – 5) + (x₃ – 5) ……. + (x_n – 5) = 60
⇒ (x₁ + x₂ + x₃ ……. + x_n) – 5n = 60
⇒ nM – 5n = 60 ………(i)
⇒ \(\sum_{i=1}^n\left(x_i-8\right)\) = 24 ⇒ nM – 8n = 24 ………(ii)
ସମୀକରଣ (i)ରୁ (ii)କୁ ବିୟୋଗ କଲେ

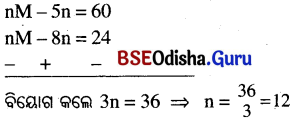
‘n’ ର ମାନ ସମୀକରଣ (i)ରେ ପ୍ରୟୋଗ କଲେ nM – 5n = 60
⇒ 12M – 60 = 60 ⇒ 12M = 120
⇒ M = \(\frac{120}{12}\) = 10
∴ n = 12 ଓ M = 10