BSE Odisha 10th Class Maths Solutions Geometry Chapter 1 ଜ୍ୟାମିତିରେ ସାଦୃଶ୍ୟ Ex 1(d)

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 1 ଜ୍ୟାମିତିରେ ସାଦୃଶ୍ୟ Ex 1(d) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 1 ଜ୍ୟାମିତିରେ ସାଦୃଶ୍ୟ Ex 1(d)

Question 1.
ବନ୍ଧନୀ ମଧ୍ଯରୁ ଠିକ୍ ଉତ୍ତର ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

(i) ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ଥିବା △ABC ରେ ∠ABC = 90°
ଏବଂ \(\overline{\mathrm{BD}}\) ⊥ \(\overline{\mathrm{AC}}\), m∠ABD = ………
[m∠BAD, m∠DBC, m∠DCB, 2m∠BAD]

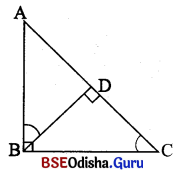
Solution:
m∠DCB

(ii) ଉପ6ର।କ୍ତ ରିତ୍ର6ର ଥିବା △ABC ରେ ∠ABC ସମ6କାଶ ଏବଂ BD AC ହେଲେ,
(a) AB2 = AD × ……….. [BC, CD, AC, BD]
(b) BC2 = AC × ……….. [DC, AD, BD, AB]
(c) BD2 = DC × ………. [AC, BC, AB, AD]
Solution:
(a) AC
(b) DC
(c) AD

Question 2.
ବମ୍ନ ଟିତ୍ର6ର ଥିର୍। △PQR ର m∠PQR = 90° ଏର୍ବ \(\overline{\mathbf{QM}}\) ⊥ \(\overline{\mathbf{PR}}\)
(i) QM = 12 6ସ.ମି. ଏବଂ PM = 6 6ସ.ମି. 6ଦ୍ର6କ , PR ନିଣ୍ଟଯ କର |
(ii) PQ = 6 6ସ.ମି. ଏବଂ PM = 3 6ସ.ମି. 6ଦ୍ର6କ , PR ନିଣ୍ଟଯ କର |
(iii) QR = 12 6ସ.ମି. ଏବଂ MR = 3 6ସ.ମି. 6ଦ୍ର6କ , PM ନିଣ୍ଟଯ କର |
(iv) PQ = 12 6ସ.ମି. ଓ RM = 3 6ସ.ମି. 6ଦ୍ର6କ , PM ନିଣ୍ଟଯ କର |
(v) PQ = 8 6ସ.ମି. ଓ QR = 15 6ସ.ମି. 6ଦ୍ର6କ , QM ଓ MR ନିଣ୍ଟଯ କର |

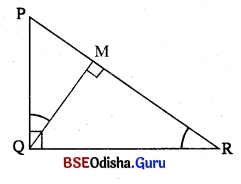
Solution:
(i) QM² = PM × RM ⇒ 12² = 6 × RM
⇒ RM = \(\frac{12^2}{6}\) 6ସ.ମି. = 24 6ସ.ମି.
PR = PM + RM = 6 6ସ.ମି. + 24 6ସ.ମି. = 30 6ସ.ମି.

(ii) PQ² = PM × PR
⇒ PR = \(\frac{\mathrm{PQ}^2}{\mathrm{PM}}\) = \(\frac{6^2}{3}\) 6ସ.ମି. = 12 6ସ.ମି.

(iii) QR² = MR × PR
⇒ PR = \(\frac{\mathrm{QR}^2}{\mathrm{MR}}\) = \(\frac{12^2}{9}\) 6ସ.ମି. = 16 6ସ.ମି.
PM = PR – MR = 16 6ସ.ମି. – 9 6ସ.ମି. = 7 6ସ.ମି. |

(iv) ମ6ନଜର PM = x 6ସ.ମି.
∴ PR = PM + MR = (x + 7) 6ସ.ମି. |
PQ² = PM . PR ⇒ 12² = x(x + 7)
⇒ x² + 7x – 144 = 0 ⇒ x² + 16x – 9x – 144 = 0
⇒ x(x + 16) -9(x + 16) = 0 ⇒ (x – 9) (x + 16) = 0
⇒ x = 9 ବ।, x = -16 (ଅସମ୍ମତ)
∴ PM = x 6ସ.ମି. = 9 6ସ.ମି.

(v) PR = \(\sqrt{\mathrm{PQ}^2+\mathrm{QR}^2}\) = \(\sqrt{8^2+15^2}\) = \(\sqrt{64+225}\) = \(\sqrt{289}\) = 17 6ସ.ମି.
QR² = MR × PR
⇒ MR = \(\frac{\mathrm{QR}^2}{\mathrm{PR}}\) = \(\frac{15 \times 15}{17}\) = \(\frac { 225 }{ 17 }\) = 13\(\frac { 4 }{ 17 }\) 6ସ.ମି.
QM² = PM × MR = (PR – MR) × MR
= (17 – \(\frac { 225 }{ 17 }\)) × \(\frac { 225 }{ 17 }\) = \(\frac { 64 }{ 17 }\) × \(\frac { 225 }{ 17 }\) ଦଙ୍ଗ6ସ.ମି.
∴ QM = \(\sqrt{\frac{64 \times 225}{17 \times 17}}\) = \(\frac{8 \times 15}{17}\) = \(\frac { 120 }{ 17 }\) = 7\(\frac { 1 }{ 17 }\) 6ସ.ମି. |

Question 3.
ବମ୍ନ ଟିତ୍ର6ର m∠ABC = m∠DCB = 90°, \(\overline{\mathbf{AC}}\) ଓ \(\overline{\mathbf{BD}}\) ର ଛେଦଦିନ୍ଦୁ O ଏବଂ \(\overline{\mathbf{AC}}\) ⊥ \(\overline{\mathbf{BD}}\) | OC = 6 6ସ.ମି. ଦଙ୍ଗ6ସ.ମି.
(i) BO ନିଶ୍ଚୟ କର;
(ii) OA ନିର୍ଣ୍ଣୟ କର;
(iii) BC ନିର୍ଣ୍ଣୟ କର;
(iv) AB ନିର୍ଣ୍ଣୟ କର; ଏବଂ
(v) CD ନିର୍ଣ୍ଣୟ କର ।

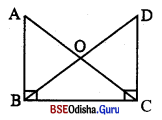
Solution:

Question 4.
△ABC ଭେ ∠ABC ସପ6କାଣ ଏବଂ \(\overline{\mathbf{B D}}\) ⊥ \(\overline{\mathbf{AC}}\) | AD = p ଏକକ ପ୍ରତେକ, ପ୍ତମାଣ କର : BC = \(\frac{q \sqrt{\mathbf{p}^2+q^2}}{p}\)
Solution:

Question 5.
△ABC ଭେ, m∠ABC = 90° ଏବଂ BD ⊥ AC ଦ୍ରେଲେ , ପ୍ରତମାଣ କର ଯେ , AB² : BC² = AD : DC |
Solution:

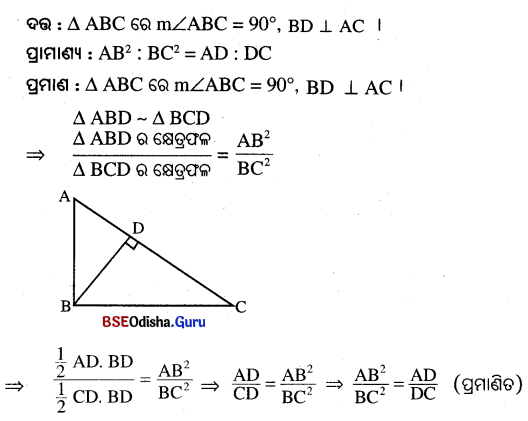
Question 6.
△ABC ଭେ, ∠ABC ସପ6କାଶ , \(\overline{\mathrm{BD}}\) ⊥ \(\overline{\mathrm{AC}}\) ଏବଂ BC² = AC.BD କ୍ତେଲେ , ପ୍ରମାଣ ଦର ଯେ \(\overline{\mathrm{BD}}\) 6ହର୍ଛି ∠ABC ତ ସପଦ୍ଦିଖଣ୍ଡକ |
Solution:

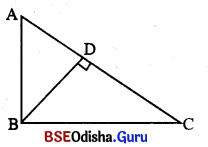
ଦର : △ABC ରେ , ∠B = 90° | \(\overline{\mathrm{BD}}\) ⊥ \(\overline{\mathrm{AC}}\) ଏବଂ BC² = AC.BD
ପ୍ରମ।ଣu : \(\overline{\mathrm{BD}}\) , ∠ABC ର ସମଦ୍ୱିଖଣ୍ଡକ |
ପ୍ରମ।ଣ : △BDC ~ △ABC ⇒ BC² = AC . AD ….(i)
କକୁ ଦଣ BC² = AC . AD ….(ii)
(i) ଓ (ii) ରୁ AC . AD = AC . BD ⇒ CD = BD ⇒ m∠DBC = m∠DCB … (iii)
କନ୍ତି △ABD ~ △BCD ⇒ m∠ABD = m∠DCB …(iv)
(iii) ଓ (iv) ର m∠DBC = m∠ABD ⇒ \(\overline{\mathrm{BD}}\) , ∠ABC ର ସମଦ୍ୱିଖଣ୍ଡ କ | (ପ୍ରମାଣିତ)

Question 7.
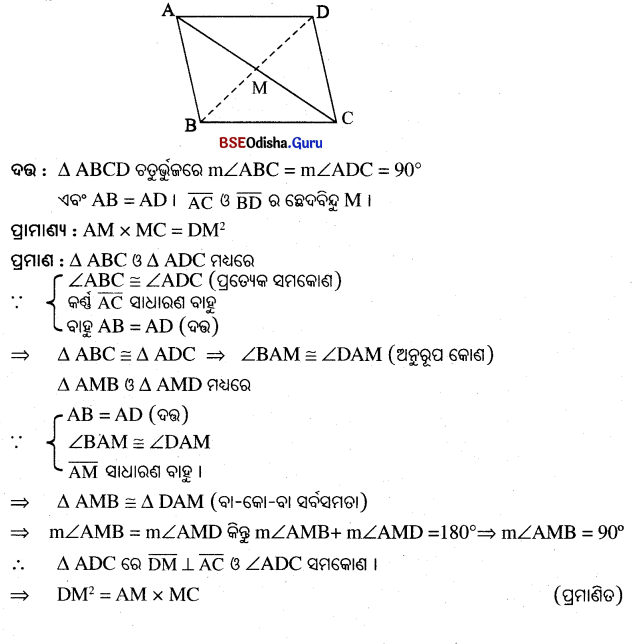
ପାଣ୍ଡଣ୍ ଚିତ୍ରରେ ଥ୍ରନା ରହୁକ୍ତିଙ ABCD ରେ m∠ABC = m∠ADC = 90° ଏବଂ AB = AD | କଣ୍ତଦ୍ରଯତ 6ଛଦଦିନ୍ଦୁ M ଦ୍ତେକେ , ପ୍ରମାଣ କର ଯେ AM × MC = DM | (ପ୍ରମେଯ 1.4 ର ସ୍ତ ଯୋଗ କରି ପ୍ରମାଣ କମା | )
Solution:

Question 8.
△ABC ରେ m∠ABC = 90°, \(\overline{\mathrm{BD}}\) ⊥ \(\overline{\mathrm{AC}}\) ଏବଂ ∠ABC ର ସମଦ୍ୱିଖଣ୍ଡ \(\overline{\mathrm{AC}}\) କ୍ E ଦିନ୍ଦୁରେ 6ଛଦ କଲୋ ପ୍ରମାଣ କର ଯେ AE² : EC² = AD : DC |
Solution:
ଦର : △ABC ରେ m∠ABC = 90° , \(\overline{\mathrm{BD}}\) ⊥ \(\overline{\mathrm{AC}}\) ଏବଂ ∠ABC ର ସମଦ୍ୱିଖଣ୍ଡ \(\overline{\mathrm{AC}}\) କ୍ E ଦିନ୍ଦୁରେ 6ଛଦ କଲୋ

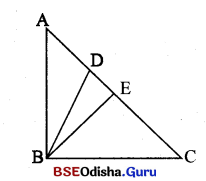
ପ୍ତାମାଣଧ୍ୟ : \(\frac{\mathrm{AE}^2}{\mathrm{EC}^2}\) = \(\frac { AD }{ DC }\)
ପ୍ତମାଣ : △ABC ରେ ∠ABC ର ସମଦ୍ୱିଖଣ୍ଡ \(\overline{\mathrm{AC}}\) କ୍ E ଦିନ୍ଦୁରେ 6ଛଦ କଲୋ
⇒ \(\frac { AB }{ BC }\) = \(\frac { AE }{ EC }\) ⇒ \(\frac{\mathrm{AE}^2}{\mathrm{EC}^2}\) = \(\frac{\mathrm{AB}^2}{\mathrm{BC}^2}\)
△ABC ରେ m∠ABC = 90° ଓ \(\overline{\mathrm{BD}}\) ⊥ \(\overline{\mathrm{AC}}\)
⇒ AB² = AD . AC ଓ BC² = CD . AC
∴ \(\frac{\mathrm{AE}^2}{\mathrm{EC}^2}\) = \(\frac{\mathrm{AB}^2}{\mathrm{BC}^2}\) = \(\frac{\mathrm{AD} \times \mathrm{AC}}{\mathrm{CD} \times \mathrm{AC}}\) = \(\frac { AD }{ CD }\) (ପ୍ରମାଣିତ)

Question 9.
△ABC ରେ , m∠BAC = 90° ଏବଂ \(\overline{\mathrm{AD}}\) ⊥ \(\overline{\mathrm{BC}}\) | ପ୍ରମାଣ କର ଯେ △ADC ର ଷ୍ଟ୍ରେତୃଫକ = \(\frac{\mathbf{A B} \times \mathbf{A C} \mathbf{C}^3}{2 \mathbf{B C} C^2}\) |

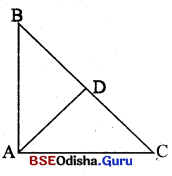
Solution:
ଦଉ : △ABC 6ର m∠BCA = 90° ଏବଂ \(\overline{\mathrm{AD}}\) | \(\overline{\mathrm{BC}}\) |
ପ୍ର।ମାଣ୍ୟ : △ADC ର ଷ୍ଟେର୍ଫଳ = \(\frac{\mathrm{AB} \times \mathrm{AC}^3}{2 \mathrm{BC}^2}\) |
ପ୍ରମାଣ : ABC ରେ m∠BAC = 90° ଓ \(\overline{\mathrm{AD}}\) ⊥ \(\overline{\mathrm{BC}}\)
⇒ AC² = CD . BC
△ABC ର ଷ୍ଟେର୍ଫଳ = \(\frac { 1 }{ 2 }\) AC × AB = \(\frac { 1 }{ 2 }\) BC × AD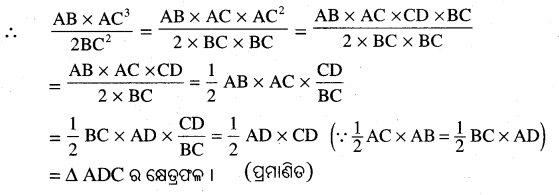 

Question 10.
△ABC ର m∠ABC ସମକୋଣ,, \(\overline{\mathrm{BD}}\) ⊥ \(\overline{\mathrm{AC}}\) ଏବଂ ∠BAC ର ଛେଦକରେ \(\overline{\mathrm{BD}}\) କୁ E ଦିନ୍ଦୁରେ ଛେଦକରେ | ପ୍ତପାଣ କର ଯେ BE² : DE² = AC : AD |
Solution:
ଦତ୍ତ : △ABC ରେ ∠ABC ସମକୋଣ, \(\overline{\mathrm{BD}}\) ⊥ \(\overline{\mathrm{AC}}\) ଏବଂ ∠BAC ର ସମଦ୍ବିଖଣ୍ଡକ \(\overline{\mathrm{BD}}\) କୁ E ବିନ୍ଦୁରେ ଛେଦକରେ ।
ପ୍ରାମାଣ୍ୟ : \(\frac{\mathrm{BE}^2}{\mathrm{DE}^2}\) : \(\frac{\mathrm{AC}}{\mathrm{AD}}\)
ପ୍ରମାଣ : △ABC ରେ ∠B ସମକୋଣ ଓ \(\overline{\mathrm{BD}}\) ⊥ \(\overline{\mathrm{AC}}\) |
⇒ AB² = AD × AC
△ABD ରେ ∠BAD ର ସମଦ୍ଦିଖଣ୍ଡକ ରଶ୍ମି \(\overline{\mathrm{BD}}\) କୁ E ରେ ଛେଦକରେ ।
⇒ \(\frac { AB }{ AD }\) = \(\frac { BE }{ DE }\)
∴ \(\frac{\mathrm{BE}^2}{\mathrm{DE}^2}\) = \(\frac{\mathrm{AB}^2}{\mathrm{AD}^2}\) = \(\frac { AD × AC }{ AD × AD }\) = \(\frac { AC }{ AD }\) (∵ AB² = AD × AC) (ପ୍ରମାଣିତ)