BSE Odisha 10th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(e)

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(e) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(e)

Question 1.
ନିମ୍ନରେ କୋଡ୍ ଆକୃତିର କେତେକ ଟୋପିର ଉଚ୍ଚତା h ଓ ବକ୍ର ଉଚ୍ଚତା l ଦତ୍ତ ଅଛି । ପ୍ରତି ଟୋପିରେ ଲାଗିଥିବା କପଡ଼ାର ପରିମାଣ ଏବଂ ତା’ର ଭୂମିର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
(i) h = 3.5 ସେ.ମି.. l = 9.1 ସେ.ମି.
(ii) h = 5.6 ସେ.ମି. l = 11.9 ସେ.ମି.
(iii) h = 3.5 ସେ.ମି. l = 12.5 ସେ.ମି.
Solution:
(i) h = 3.5 ସେ.ମି. ଓ l = 9.1 ସେ.ମି. |
r = \(\sqrt{l^2-\mathrm{h}^2}\) = \(\sqrt{(9.1)^2-(3.5)^2}\) = \(\sqrt{82.81-12.25}\) = \(\sqrt{70.56}\) = 8.4 ସେ.ମି.
∴ ଟୋପିରେ ଲାଗିଥିବା କପଡ଼ାର ପରିମାଣ = πrl
= \(\frac { 22 }{ 7 }\) × 8.4 × 9.1 ବାଗ ସେ.ମି. = 240.24 ବାଗ ସେ.ମି.
∴ ଭୂମିର କ୍ଷେତ୍ରଫଳ = πr² = \(\frac { 22 }{ 7 }\) × 8.4 × 8.4 ବାଗ ସେ.ମି. = 221.76 ବାଗ ସେ.ମି.

(ii) h = 5.6 ସେ.ମି. ଓ l = 11.9 ସେ.ମି.
r = \(\sqrt{l^2-\mathrm{h}^2}\) = \(\sqrt{(11.9)^2-(5.6)^2}\)
= \(\sqrt{141.61-31.36}\) = \(\sqrt{110.25}\) = 10.5 ସେ.ମି.
∴ କପଡାର ପରିମାଣ = πrl = \(\frac { 22 }{ 7 }\) × 10.5 × 11.9 = 392.70 ବାଗ ସେ.ମି.
∴ ଭୂମିର କ୍ଷେତ୍ରଫଳ = πr² = \(\frac { 22 }{ 7 }\) × 10.5 × 10.5 = 346.50 ବାଗ ସେ.ମି.

(iii) h = 3.5 ସେ.ମି. ଓ l = 12.5 ସେ.ମି.
r = \(\sqrt{l^2-\mathrm{h}^2}\) = \(\sqrt{(12.5)^2-(3.5)^2}\) ସେ.ମି.
= \(\sqrt{(12.5+3.5)(12.5-3.5)}\) ସେ.ମି. = \(\sqrt{16 \times 9}\) ସେ.ମି. = 12 ସେ.ମି.
∴ କପଡାର ପରିମାଣ = πrl = \(\frac { 22 }{ 7 }\) × 12 × 12.5 ବାଗ ସେ.ମି. = 471.43 ବାଗ ସେ.ମି.
∴ ଭୂମିର କ୍ଷେତ୍ରଫଳ = πr² = \(\frac { 22 }{ 7 }\) × 12 × 12 = 452.57 ବାଗ ସେ.ମି.

Question 2.
ନିମ୍ନରେ କୋଡ୍ ଆକୃତିର ତିନୋଟି ତମ୍ବୁର ବକ୍ର ଉଚ୍ଚତା l ଓ ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ ଦତ୍ତ ଅଛି । ପ୍ରତି ତନ୍ତୁର ଭିତରର ଆୟତନ ଓ ତମ୍ବୁରେ ଲାଗିଥିବା କପଡ଼ାର ପରିମାଣ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
(i) r = 10.5 ମି. ଓ l = 14.5 ମି.
(ii) h = 24 ମି. l = 25 ମି.
Solution:
(i) r = 10.5 ମି. ଓ l = 14.5 ମି.
h = \(\sqrt{l^2-\mathrm{r}^2}\) = \(\sqrt{(14.5)^2-(10.5)^2}\) ମି.
= \(\sqrt{(14.5+10.5)(14.5-10.5)}\) ମି. = \(\sqrt{25 \times 4}\) ମି. = 10 ମି.
∴ ଆୟତନ = \(\frac { 1 }{ 3 }\) πr²h = \(\frac { 1 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × 10.5 × 10.5 × 10 ପନ.ମି. = 1155 ପନ.ମି.
∴ ଉପରେ ଲାଗିଥିବା କପରାଇ ପରିମାଣ = πrl = \(\frac { 22 }{ 7 }\) × 10.5 × 14.5 = 478.5 ବାଗ ମି.

(ii) h = 24 ମି. l = 25 ମି.
r = \(\sqrt{l^2-\mathrm{h}^2}\) = \(\sqrt{25^2-24^2}\) ମି. = \(\sqrt{625-576}\) ମି. = √49 ମି. = 7 ମି
∴ ଆୟତନ = \(\frac { 1 }{ 3 }\) πr²h = \(\frac { 1 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × 7 × 7 × 24 = 1232 ଶଳା.ମି.
∴ ଉପରେ ଲାଗିଥିବା କପରାଇ ପରିମାଣ = πrl = \(\frac { 22 }{ 7 }\) × 7 × 25 = 550 ବାଗ ମି.

Question 3.
ଗୋଟିଏ କୋନ୍‌ର ଆୟତନ 12936 ଘନ ମିଟର । ଏହାର ଉଚ୍ଚତା 28 ମିଟର ହେଲେ ଭୂମିର କ୍ଷେତ୍ରଫଳ ଓ ବକ୍ରତଳର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
ଗୋଟିଏ କୋନ୍‌ର ଆୟତନ 9240 ଘନ ଏକକ । ଏହାର ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ 21 ଏକକ ହେଲେ କୋନ୍‌ର ବକ୍ରତଳର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ମନେକର କୋନ୍‌ର ବ୍ୟାସାର୍ଦ୍ଧ = r ମି. । ∴ ଆୟତନ = \(\frac { 1 }{ 3 }\)πr²h ପ.ମି.
ପ୍ରଣାଳୀବାରେ \(\frac { 1 }{ 3 }\)πr²h = 12936 ଗନମିଟର, ⇒ \(\frac { 1 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × r² × 28 = 12936
⇒ r² = \(\frac{12936 \times 21}{22 \times 28}\) = 441 ⇒ r = √441 = 21
∴ ଭୂମିର କ୍ଷେତ୍ରଫଳ = πr² = \(\frac { 22 }{ 7 }\) × 21 × 21 ବର୍ଗମିଟର = 1386 ବର୍ଗମିଟର
ଦକ୍ତ ଭଳତା (l) = l = \(\sqrt{h^2+r^2}\) = \(\sqrt{28^2+21^2}\) = 35 ମି.
∴ ମନେକର କ୍ଷେତ୍ରଫଳ = πrl = \(\frac { 22 }{ 7 }\) × 21 × 35 = 2310 ବର୍ଗମିଟର

(ii) କୋନ୍‌ର ଆୟତନ = 9240 ଘନ ଏକକ, ବ୍ୟାସାର୍ଦ୍ଧ (r) = 21 ଏକକ
ମନେକର କୋନ୍‌ର ଉଚ୍ଚତା = h ଏକକ । କୋନ୍‌ର ଆୟତନ = \(\frac { 1 }{ 3 }\)πr²h ଘନ ଏକକ ।
ପ୍ରଶ୍ନନୁସାରେ \(\frac { 1 }{ 3 }\)πr²h = 9240 ଘନ ଏକକ ⇒ \(\frac { 1 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × 21 × 21 × h = 9240
⇒ h = \(\frac{9240}{22 \times 21}\) ଏକକ = 20 ଏକକ
∴ ଦକ୍ତ ଭଳତା (l) = \(\sqrt{h^2+r^2}\) = \(\sqrt{20^2+21^2}\) ଏକକ = \(\sqrt{400+441}\) ଏକକ = 29 ଏକକ
∴ ମନେକର କ୍ଷେତ୍ରଫଳ = πrl = \(\frac { 22 }{ 7 }\) × 21 × 29 ବର୍ଗମିଟର = 1914 ବର୍ଗ ଏକକ |

Question 4.
(i) ଗୋଟିଏ କୋନ୍‌ର ବଜ୍ରତଳର କ୍ଷେତ୍ରଫଳ 550 ବର୍ଗ ସେ.ମି. ଏବଂ ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ 7 ସେ.ମି. ହେଲେ କୋଟିର ଆୟତନ ଏବଂ ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
(ii) ଗୋଟିଏ କୋନ୍‌ର ବକ୍ରତଳର କ୍ଷେତ୍ରଫଳ 4070 ବର୍ଗ ସେ.ମି. ଏବଂ ବକ୍ର ଉଚ୍ଚତା 17 ସେ.ମି. ହେଲେ ତାହାର ଭୂମିର କ୍ଷେତ୍ରଫଳ ଓ ଆୟତନ ନିରୂପଣ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
(i) କୋନ୍‌ର ବକ୍ରତଳର କ୍ଷେତ୍ରଫଳ = 550 ବର୍ଗ ସେ.ମି., ବ୍ୟାସାର୍ଦ୍ଧ (r) = 7 ସେ.ମି.
ମନେକର କୋନ୍‌ର ଉଚ୍ଚତା = l ସେ.ମି. ଓ କୋନ୍‌ର ବଜ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = πrl ବର୍ଗ ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ πrl = 550 ବର୍ଗ ସେ.ମି. ⇒ \(\frac { 22 }{ 7 }\) × 7 × l = 550 ⇒ l = \(\frac { 550 }{ 22 }\) = 25 ସେ.ମି.
∴ କୋନ୍‌ର ଉଚ୍ଚତା (h) = \(\sqrt{l^2-\mathrm{r}^2}\) = \(\sqrt{25^2-7^2}\) = \(\sqrt{625-49}\) = \(\sqrt{576}\) = 24 ସେ.ମି.
∴ କୋନ୍‌ର ଆୟତନ = \(\frac { 1 }{ 3 }\) πr²h = \(\frac { 1 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × 7² × 24 = 22 × 7 × 8 = 1232 ମନ ସେ.ମି.
ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = πr (l + r) = \(\frac { 22 }{ 7 }\) × 7 (25 + 7) ଦଗ ସେ.ମି.
= 22 × 32 = 704 ଦଗ ସେ.ମି.

(ii) କୋନ୍‌ର ବକ୍ରତଳର କ୍ଷେତ୍ରଫଳ = 4070 ଦଗ ସେ.ମି. ଜନ୍ତୁ ଭଳତା (l) = 37 ସେ.ମି. |
ମନେକର କୃମିର ବ୍ୟାଗାଦ = r ସେ.ମି. ସେ.ମି. ଓ କୋନ୍‌ର ବକ୍ରତଳର କ୍ଷେତ୍ରଫଳ = πrl ବର୍ଗ ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ πrl = 4070 ବର୍ଗ ସେ.ମି.. ⇒ \(\frac { 22 }{ 7 }\) × r × 37 = 4070
⇒ r = \(\frac{4070 \times 7}{22 \times 37}\) ସେ.ମି. = 35 ସେ.ମି.
କୋନ୍‌ର ଉଚ୍ଚତା (h) = \(\sqrt{l^2-\mathrm{r}^2}\) = \(\sqrt{37^2-35^2}\)
= \(\sqrt{(37+35)(37-35)}\) = \(\sqrt{72 \times 2}\) = 12 ସେ.ମି.
∴ ଦୃମିର କ୍ଷେତ୍ରଫଳ = πr² = \(\frac { 22 }{ 7 }\) × (35)² ବର୍ଗ ସେ.ମି. = 3850 ବର୍ଗ ସେ.ମି..
∴ ଆୟତନ = \(\frac { 1 }{ 3 }\) πr²h = \(\frac { 1 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × (35)² × 12 ମନ ସେ.ମି. = 15400 ମନ ସେ.ମି.

Question 5.
ଯେଉଁ କୋନ୍‌ର ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 2816 ବର୍ଗ ସେ.ମି. ଏବଂ ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ 14 ସେ.ମି. ତାହାର ଆୟତନ ଏବଂ ବଜ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ସ୍ଥିର କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
କୋନ୍‌ର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2816 ବର୍ଗ ସେ.ମି., ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ (r) = 14 ସେ.ମି. ।
ମନେକର ବକ୍ରଉଚ୍ଚତା = l ସେ.ମି. ଓ କୋନ୍‌ର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = πr(l + r) ବର୍ଗ ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, πr (l + r) = 2816 ବର୍ଗ ସେ.ମି. ⇒ \(\frac { 22 }{ 7 }\) × 14 (l + 14) = 2816
⇒ l + 14 = \(\frac{2816 \times 7}{22 \times 14}\) = 64 ⇒ l = 64 – 14 = 50 ସେ.ମି.
କୋନ୍‌ର ଉଚ୍ଚତା (h) = \(\sqrt{l^2-\mathrm{r}^2}\) = \(\sqrt{50^2-14^2}\) = \(\sqrt{64 \times 36}\) = 48 ସେ.ମି.
∴ ଆୟତନ = \(\frac { 1 }{ 3 }\) πr²h = \(\frac { 1 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × 14 × 14 × 48 = 9856 ମନ ସେ.ମି.
∴ ବକ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = πrl = \(\frac { 22 }{ 7 }\) × 14 × 50 ବର୍ଗ ମି. = 2200 ବର୍ଗ ମି.

Question 6.
ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 1386 ବର୍ଗ ସେ.ମି. ଏବଂ ବକ୍ରତଳର କ୍ଷେତ୍ରଫଳ 770) ବର୍ଗ ସେ.ମି. ହୋଇଥିବା କୋଟିର ଆୟତନ ନିରୂପଣ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ମନେକର କୋନ୍‌ର ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ = r ସେ.ମି. ଓ ବକ୍ର ଉଚ୍ଚତା = h ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, πr (l + r) = 1386 ଦଗ ସେ.ମି. πrl = 770 ଦଗ ସେ.ମି.
∴ πr² = πr (l + r) = (1386 – 770) ଦଗ ସେ.ମି. = 616 ଦଗ ସେ.ମି.
⇒ \(\frac { 22 }{ 7 }\) × r² = 616 ⇒ r² = \(\frac{616 \times 7}{22}\) = 28 × 7 = 196 ⇒ r = √196 = 14
ଦଇ ଅଛି πrl = 770 ⇒ \(\frac { 22 }{ 7 }\) × 14 × l = 770
⇒ l = \(\frac { 770 }{ 44 }\) = 17.5 ସେ.ମି.
କୋନ୍‌ର ଉଚ୍ଚତା (h) = \(\sqrt{l^2-\mathrm{r}^2}\) = \(\sqrt{(17.5)^2-(14)^2}\) = \(\sqrt{(17 \cdot 5+14)(17 \cdot 5-14)}\) = \(\sqrt{31.5 \times 3.5}\) = 10.5 ସେ.ମି.
∴ କୋନ୍‌ର ଆୟତନ = \(\frac { 1 }{ 3 }\) πr²h = \(\frac { 1 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × 14 × 14 × 10.5 = 2156 ମନ ସେ.ମି.

Question 7.
(i) ଆୟତନ 12936 ଶନ ସେ.ମି. ଏବଂ r : h = 3 : 4 ହୋଇଥିବା ଏକ କୋଳର ବିକ୍ତତଳଭ ଯେତ୍ରଫଳ ମିଳ କର | (π ≃ \(\frac { 22 }{ 7 }\))
(ii) ଆୟତନ 17248 ଶନ ସେ.ମି. ଏବଂ r : l = 4 : 5 ଥିବା କୋଟିଏ କୋଳର ବିକ୍ତତଳଭ ଯେତ୍ରଫଳ ନିଶ୍ରଣ କର | (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
(i) r : h = 3 : 4 | ମନେକର r = 3x ସେ.ମି. ଓ h = 4x ସେ.ମି.
ଦନ୍ତ ଚଳତା (l) = \(\sqrt{\mathrm{r}^2+\mathrm{h}^2}\) = \(\sqrt{(3 x)^2+(4 x)^2}\) = \(\sqrt{25 x^2}\) = 5x ସେ.ମି.
ଆୟତନ = \(\frac { 1 }{ 3 }\) πr²h = \(\frac { 1 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × 3x × 3x × 4x = \(\frac { 264 }{ 7 }\) x³ ମନ ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, \(\frac { 264 }{ 7 }\) x³ = 12936 ⇒ x³ = \(\frac{12936 \times 7}{264}\) = 343 ⇒ x = \(\sqrt[3]{343}\) = 7
∴ କୋନ୍‌ର ବିକ୍ତତଳଭ ଯେତ୍ରଫଳ = πrl = \(\frac { 22 }{ 7 }\) × 3x × 5x
= \(\frac { 22 }{ 7 }\) × 3 × 7 × 5 × 7 = 2310 ଦଗ ସେ.ମି.

(ii) r : l = 4 : 5 | ମନେକର r = 4x ମି. ଦ୍ରେଲେ l = 5x ମି.
କୋନ୍‌ର ଚଳତା (h) = \(\sqrt{l^2-\mathrm{r}^2}\) = \(\sqrt{(5 x)^2-(4 x)^2}\) = \(\sqrt{9 x^2}\) = 3x ମି.
ଆୟତନ = \(\frac { 1 }{ 3 }\) πr²h = \(\frac { 1 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × 4x × 4x × 3x ଶନ.ମି. = \(\frac { 352 }{ 7 }\) x³ ପନ. ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, \(\frac { 352 }{ 7 }\) x³ = 17248 ⇒ x³ = \(\frac{17248 \times 7}{352}\) = 343 ⇒ x = \(\sqrt[3]{343}\) = 7
∴ କୋନ୍‌ର ବିକ୍ତତଳଭ ଯେତ୍ରଫଳ = πrl = \(\frac { 22 }{ 7 }\) × 3x × 5x ଦଗ ମି.
= \(\frac { 22 }{ 7 }\) × 4 × 7 × 5 × 7 ଦଗ ମି. = 3080 ଦଗ ମି.

Question 8.
(i) (i) ଦୁଇଟି କୋନ୍‌ର ବ୍ୟାସାର୍ଦ୍ଧ ଅନୁପାତ 3 : 5 ଓ ଉଚ୍ଚତାର ଅନୁପାତ 1 : 3 ହେଲେ ସେ ଦୁଇଟିର ଆୟତନର ଅନୁପାତ ସ୍ଥିର କର ।
(ii) ଦୁଇଟି କୋନ୍‌ର ବ୍ୟାସାର୍ଦ୍ଧ ଅନୁପାତ 2 : 7 ଓ ବକ୍ରଉଚ୍ଚତାର ଅନୁପାତ 3 : 8 ହେଲେ ଉକ୍ତ କୋୟର ବକ୍ରତଳର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ ଦୁଇଟି କର ।
(iii) ଦୁଇଟି କୋନ୍‌ର ଭୂମିର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ 1 : 9 ଏବଂ ହେଲେ ସେ ଦୁଇଟିର ବକ୍ରଉଚ୍ଚତାର ଅନୁପାତ 5 : 21 ହେଲେ ପେ ଦୁକ୍ମଣକ୍ନତାର ଅନୁପାତ ନିର କର |
Solution:
ମନେକର ପ୍ରଥମ ଓ ଦ୍ୱିତୀୟ କୋନ୍‌ର ବ୍ୟାସାର୍ଷ, ଉଚ୍ଚତା ଓ ବକ୍ର ଉଚ୍ଚତା ଯଥାକ୍ରମେ r, h₁, l₁ ଏବଂ r₂, h₂, l₂ |
(i) \(\frac{r_1}{r_2}\) = \(\frac { 3 }{ 5 }\) ଓ \(\frac{h_1}{h_2}\) = \(\frac { 1 }{ 3 }\)
∴ \(\frac{V_1}{V_2}\) = \(\frac{\frac{1}{3} \pi r_1^2 h_1}{\frac{1}{3} \pi r_2^2 h_2}\) = \(\frac{r_1 \times r_1 \times h_1}{r_2 \times r_2 \times h_2}\) = \(\frac{3}{5}\) × \(\frac{3}{5}\) × \(\frac{1}{3}\) 3 : 25
∴ କୋନ୍ ଦ୍ବୟର ଆୟତନର ଅନୁପାତ 3 : 25 |

(ii) \(\frac{r_1}{r_2}\) = \(\frac { 2 }{ 7 }\) ଓ \(\frac{l_1}{l_2}\) = \(\frac { 3 }{ 8 }\)
∴ \(\frac{S_1}{S_2}\) = \(\frac{\pi \mathrm{r}_1 l_1}{\pi \mathrm{r}_2 l_2}\) = \(\frac{r_1}{r_2}\) × \(\frac{l_1}{l_2}\) = \(\frac { 2 }{ 7 }\) × \(\frac { 3 }{ 8 }\) = 3 : 28
∴ କୋନ୍ ଦୁଇଟିର ବକ୍ରତଳର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ 3 : 28 |

(iii) \(\frac{\pi r_1^2}{\pi r_2{ }^2}\) = \(\frac { 1 }{ 9 }\) ⇒ \(\frac{r_1}{r_2}\) = \(\frac { 1 }{ 9 }\) ⇒ \(\frac{r_1}{r_2}\) = \(\frac { 1 }{ 3 }\)
\(\frac{\pi r_1 l_1}{\pi r_2 l_2}\) = \(\frac{r_1}{r_2}\) × \(\frac{l_1}{l_2}\) = \(\frac { 1 }{ 3 }\) × \(\frac{l_1}{l_2}\)
ପ୍ରଶ୍ନନୁସାରେ, \(\frac { 1 }{ 3 }\) × \(\frac{l_1}{l_2}\) = \(\frac { 5 }{ 21 }\) ⇒ \(\frac{l_1}{l_2}\) = \(\frac { 5 }{ 7 }\)
∴ କୋନ୍‌ଦ୍ବୟର ବକ୍ରଉଚ୍ଚତାର ଅନୁପାତ 5 : 7 |

Question 9.
(i) ଏକ କୋନ୍‌ର ଉଚ୍ଚତା ଏହାର ବକ୍ରଉଚ୍ଚତାର ଅଧା । କୋନ୍‌ର ବ୍ୟାସାର୍କ୍ 5√3 ସେ.ମି. ହେଲେ ଏହାର ଘନଫଳ ନିଶ୍ଚୟ କର । (π ≃ 3.14)
(ii) ଏକ କୋନ୍‌ର ଉଚ୍ଚତା ଏହାର ବ୍ୟାସାର୍ଦ୍ଧର ଅଧା । କୋନ୍‌ର ବକ୍ରଉଚ୍ଚତା 50 ସେ.ମି. ହେଲେ ଏହାର ଘନଫଳ ନିର୍ଣ୍ଣୟ କର । (π ≃ 3.14)
(iii) ଏକ କୋନ୍‌ର ଉଚ୍ଚତା ଓ ଏହାର ଭୂମିର ବ୍ୟାସର ଅନୁପାତ 2 : 3 ଏବଂ ଏହାର ବକ୍ରଉଚ୍ଚତା 20 ସେ.ମି. ହେଲେ ଏହାର ଘନଫଳ ନିର୍ଣ୍ଣୟ କର । (n ≃ √10 )
Solution:
(i) ମନେକର କୋନ୍‌ର ଉଚ୍ଚତା (h) = x ସେ.ମି., ବକ୍ର ଉଚ୍ଚତା (l) = 2x ସେ.ମି.
ଦ୍ୟାପାଦ (r) = \(\sqrt{l^2-\mathrm{h}^2}\) = \(\sqrt{(2 x)^2-(x)^2}\) = √3 x ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, √3x = 5√3 ⇒ x = 5
∴ କୋନ୍‌ର ଘନଫଳ = \(\frac { 1 }{ 3 }\) πr²h = \(\frac { 1 }{ 3 }\) × 3.14 × (√3x)² × x ପନ. ସେ.ମି.
= \(\frac { 3.14 }{ 3 }\) × 5√3 × 5√3 × 5 ପନ. ସେ.ମି. = 392.5 ପନ. ସେ.ମି.

(ii) ମନେକର କୋନ୍‌ର ଉଚ୍ଚତା (h) = x ସେ.ମି. ।
ବ୍ୟାସାର୍ଦ୍ଧ (r) = 2x ସେ.ମି.
ବକ୍ତ ଭଳତା (l) = \(\sqrt{\mathrm{r}^2+\mathrm{h}^2}\) = \(\sqrt{(2 x)^2+(x)^2}\) ସେ.ମି. = √5x ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, √5x = 50 ⇒ x = \(\frac{50}{\sqrt{5}}\) = 10√5
r = 2x ସେ.ମି. = 20 √5 ସେ.ମି. h = x ସେ.ମି. = 10 √5 ସେ.ମି.
∴ କୋନ୍‌ର ଘନଫଳ = \(\frac { 1 }{ 3 }\) πr²h = \(\frac { 1 }{ 3 }\) × 3.14 × 20√5 × 20√5 × 10√5
= \(\frac{62800 \sqrt{5}}{3}\) = 20933.33√5 ପନ. ସେ.ମି.

(iii) ମନେକର କୋନ୍‌ର ଉଚ୍ଚତା (h) = 2x ସେ.ମି. ଭୂମିର ବ୍ୟାପ = 3x ସେ.ମି.
ଭୂମିର ବ୍ୟାପ।ଘ = \(\frac { 3x }{ 2 }\) ସେ.ମି.

Question 10.
ଏକ ସମଘନାକାର କାଠଖଣ୍ଡର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ 21 ସେ.ମି. । ଏଥୁରୁ କଟାଯାଇ ମିଳିଥିବା ବୃହତ୍ତମ ଆୟତନ ବିଶିଷ୍ଟ କୋନ୍‌ର ଘନଫଳ ଓ ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ସମଘନାକାର କାଠଖଣ୍ଡର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ = 21 ସେ.ମି. ଏଥୁରୁ କଟାଯାଇ ମିଳିଥିବା ବୃହତ୍ତମ ଆୟତନ ବିଶିଷ୍ଟ କୋନ୍‌ର ଭୂମିର ବ୍ୟାପ = 21 ସେ.ମି.
∴ଦୈର୍ଘ୍ୟ (r) = \(\frac { 21 }{ 2 }\) ସେ.ମି.
କୋନ୍‌ର ଘନଫଳ (h) = 21 ସେ.ମି.
∴ ଘନଫଳ = \(\frac { 1 }{ 3 }\) πr²h = \(\frac { 1 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × \(\frac { 21 }{ 2 }\) × \(\frac { 21 }{ 2 }\) × 21 ପନ. ସେ.ମି. = 2425.5 ପନ. ସେ.ମି.

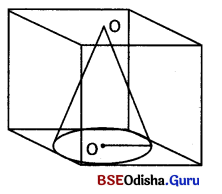
ଦକୁ ଭଲଭା (l) = \(\sqrt{r^2+h^2}\) = \(\sqrt{\left(\frac{21}{2}\right)^2+21^2}\) ସେ.ମି.
= \(\sqrt{\frac{21^2}{4}+21^2}\) ସେ.ମି. = 21 × \(\frac{\sqrt{5}}{2}\) ସେ.ମି.
∴ ସମଘନାକାର କ୍ଷେତ୍ରଫଳ = πr (l + r) = \(\frac { 22 }{ 7 }\) × \(\frac { 21 }{ 2 }\) × \(\left(\frac{21 \sqrt{5}}{2}+\frac{21}{2}\right)\)
= 33 × \(\frac { 21 }{ 2 }\) (√5 + 1) = 693 \(\frac{\sqrt{5}+1}{2}\) = 346.5 (√5 + 1) ଦଗ ସେ.ମି.

Question 11.
ବୃତ୍ତକଳା ଆକୃତିର ଗୋଟିଏ ଟିଣପତ୍ରକୁ ମୋଡ଼ି ତା’ର ଦୁଇ ପାଖର ବ୍ୟାସାର୍ଷକୁ ଯୋଡ଼ି ଝଳାଇ କରି କୋନ୍ ଆକାର ବିଶିଷ୍ଟ ଏକ ପାତ୍ର ପ୍ରସ୍ତୁତ କରାଗଲା । ଟିଣପତ୍ରଟିର ବ୍ୟାସାର୍ଦ୍ଧ 12 ସେ.ମି. ଏବଂ ବ୍ୟାସାର୍ଦ୍ଧଦ୍ଵୟର ମଧ୍ୟବର୍ତୀ କୋଣ ପରିମାଣ 120° ହେଲେ ପ୍ରସ୍ତୁତ ପାତ୍ରଟିରେ କେତେ ପାଣି ରହିପାରିବ ?
ସମାଧାନ :
ଟିଣପତ୍ରର ବ୍ୟାସାର୍ଦ୍ଧ (1) = 12 ସେ.ମି.
ବକ୍ର ଉଚ୍ଚତା (l) = 12 ସେ.ମି.
କେନ୍ଦ୍ରସ୍ଥ କୋଣର ପରିମାଣ (θ) =120°
∴ବୃତ୍ତକଳାର ଚାପର ଦୈର୍ଘ୍ୟ (L) = \(\frac{\theta \pi r}{180}\)
= \(\frac{120 \pi \times 12}{180}\) = 8π ସେ.ମି.

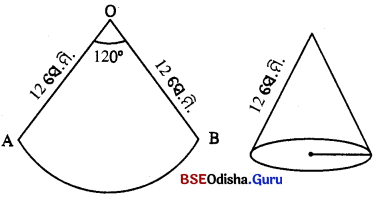
∴ କୋନ୍‌ର ଭୂମିର ପରିଧୂ = 8π ସେ.ମି.
ମନେକର କୋନ୍‌ର ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ r ସେ.ମି.
∴ 2πr = 8π = 2 × π × r = 8π ⇒ r = 4
କୋଣର (h) = \(\sqrt{l^2-\mathrm{r}^2}\) = \(\sqrt{12^2-4^2}\) = \(\sqrt{144-16}\) = \(\sqrt{128}\) = 8√2 ସେ.ମି.
∴ କୋନ୍‌ର ଣପତ୍ରକୁ = \(\frac { 1 }{ 3 }\)πr²h = \(\frac { 1 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × 4 × 4 × 8√2
= \(\frac{2816 \sqrt{2}}{21}\) ଦଗ ସେ.ମି.
∴ ପ୍ରସ୍ତୁତ ପାତ୍ରରେ \(\frac{2816 \sqrt{2}}{21}\) ଘନ ସେ.ମି. ପାଣି ରହିପାରିବ ।

Question 12.
ଗୋଟିଏ ନିଦା କୋନ୍‌ର ଭୂମିର ବ୍ୟାସ 6 ସେ.ମି. ଓ ଉଚ୍ଚତା 8 ସେ.ମି. । ଏହାକୁ ଆଂଶିକ ଜଳପୂର୍ଣ୍ଣ ଏକ ସିଲିଣ୍ଡର ଆକାରର ପାତ୍ର ମଧ୍ୟରେ ସମ୍ପୂର୍ଣ୍ଣ ରୂପେ ବୁଡ଼ାଇ ଦିଆଗଲା । ସିଲିଣ୍ଡରର ଭିତରର ବ୍ୟାସ 8 ସେ.ମି. ହେଲେ କୋନ୍‌ର ଥିବା କଳାସ୍ତର କେତେ ଦାନ୍ତି ପାଳିତ ?
Solution:
କୋନ୍‌ର ବ୍ୟାସାର୍ଦ୍ଧ (r) = \(\frac { ବ୍ୟାସ }{ 3 }\) = \(\frac { 6 }{ 2 }\) = 3 ସେ.ମି. ଓ ଉଚ୍ଚତା (h) = 8 ସେ.ମି.
∴ କୋନ୍‌ର ଘନଫଳ = \(\frac { 1 }{ 3 }\) πr²h = \(\frac { 1 }{ 3 }\) × π × 3² × 8 ପନ. ସେ.ମି. = 24π ପନ. ସେ.ମି.
ସିଲିଣ୍ଡରର ଭୂମିର କ୍ଷେତ୍ରଫଳ = πr² = π(\(\frac { 8 }{ 2 }\))² = 16π ଦଗ ସେ.ମି.
କୋନ୍‌ର ଆୟତନ = ବୃଦ୍ଧି ପାଇଥିବା ଭଲଭ ଆୟତନ = 16π × କଲ ପ୍ତରର ପ୍ରତିର ଭଳତା |
∴ କଳସ୍ତରର ଉଲତା ହନିସାର = \(\frac { 24π }{ 16π }\) ସେ.ମି. = 1.5 ସେ.ମି.

Question 13.
ଗୋଟିଏ ତମ୍ବୁର ନିମ୍ନ ଅଂଶ ସିଲିଣ୍ଡର ଆକୃତି ବିଶିଷ୍ଟ ଯାହାର ବ୍ୟାସାର୍ଦ୍ଧ 35 ମି. ଓ ଉଚ୍ଚତା 8 ମି. ଏବଂ ଊର୍ଥାଂଶ 35 ମି. ବ୍ୟାସାର୍ଦ୍ଧ ଏବଂ 12 ମି. ଉଚ୍ଚତା ବିଶିଷ୍ଟ ଏକ କୋଡ୍ ଆକାରର । ତମ୍ବୁଟିକୁ ପ୍ରସ୍ତୁତ କରିବାପାଇଁ କେତେ ବର୍ଗମିଟର କପଡ଼ା ଲାଗିଥ୍ ସ୍ଥିର କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ସିଲିଣ୍ଡରର ବ୍ୟାସାର୍ଦ୍ଧ (r) = 35 ମି. ଉଚ୍ଚତା (h) = 8 ମି.
ସିଲିଣ୍ଡରର ବଜ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πrh
= 2 × \(\frac { 22 }{ 7 }\) × 35 × 8 = 1760 ଦଗ.ମି.

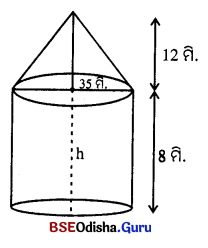
କୋନ୍‌ର ବ୍ୟାସାର୍ଦ୍ଧ (r) = 35 ମି. ଓ ଉଚ୍ଚତା (h) = 12 ମି.
ବକ୍ତ ଭଳତା (l) = \(\sqrt{r^2+h^2}\) = \(\sqrt{35^2+12^2}\) ମି. = \(\sqrt{1225+144}\) ମି. = \(\sqrt{1369}\) ମି. = 37 ମି.
∴ କୋନ୍‌ର ବକ୍ରତଳର କ୍ଷେତ୍ରଫଳ = πrl

Question 14.
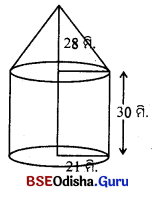
ଏକ ତମ୍ବୁର ନିମ୍ନ ଅଂଶ 30 ମି. ଉଚ୍ଚତା ବିଶିଷ୍ଟ ସରଳ ବୃତ୍ତ ଭୂମିକ ସିଲିଣ୍ଡର ଓ ଉପର ଅଂଶ କୋଡ୍ ଆକାର ବିଶିଷ୍ଟ । ଏହାର ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ 21 ମି. ଏବଂ ଭୂପୃଷ୍ଠରୁ ତମ୍ବୁଶୀର୍ଷର ଉଚ୍ଚତା 58 ମି. ହେଲେ ତମ୍ବୁରେ ବ୍ୟବହୃତ କ୍ୟାନ୍‌ସ୍‌ର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ପିଲିଣ୍ଡରର ବ୍ୟାସାଦି (r) = 21 ମି., h = 30 ମି.
ସିଲିଣ୍ଡରର ବଜ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πrh
= 2 × \(\frac { 22 }{ 7 }\) × 21 × 30 = 3960 ଦଗ.ମି.

Question 15.
ଗୋଟିଏ ଜଳପୂର୍ଣ୍ଣ କୋନ୍ ଆକାର ବିଶିଷ୍ଟ ଏକ ପାତ୍ରର ଉପର ବୃତ୍ତାକାର ଧାରର ବ୍ୟାସାର୍ଦ୍ଧ 2.5 ସେ.ମି. ଏବଂ ଗଭୀରତା 11 ସେ.ମି. | 0.25 ସେ.ମି. ବ୍ୟାସାର୍କ ବିଶିଷ୍ଟ କେତେଗୋଟି ସୀସା ଗୋଲି ଏହା ମଧ୍ୟକୁ ପକାଇଲେ ଏଥ‌ିରେ ଥିବା ଜଳର \(\frac { 2 }{ 5 }\) ଅଂଶ ବାହାରକୁ ଅପସାରିତ ହୋଇଯିବ, ସ୍ଥିର କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ଜଳପୂର୍ଣ କୋନ୍ ଆକାର ବିଶିଷ୍ଟ ପାତ୍ରର ବ୍ୟାସାର୍ଦ୍ଧ (r) = 2.5 ସେ.ମି.
ଏବଂ ଗଭୀରତା ବା ଉଚ୍ଚତା (h) = 11 ସେ.ମି.
କୋନ୍‌ରେ ଥ‌ିବା ଜଳର ଆୟତନ = \(\frac { 1 }{ 3 }\) πr²h = \(\frac { 1 }{ 3 }\) π × (2.5)² × 11 ଣନ ସେ.ମି.
ଅପସାରିତ ଜଳର ପରିମାଣ = \(\frac { 1 }{ 3 }\) π × (2.5)² × 11 × \(\frac { 2 }{ 5 }\) ଣନ ସେ.ମି.
ସୀସାଗୋଲିର ବ୍ୟାସାର୍ଦ୍ଧ (r₁) = 0.25 ସେ.ମି.
ସୀସାଗୋଲିର ଆୟତନ = \(\frac { 4 }{ 3 }\) π × (0.25)³ ଣନ ସେ.ମି.

Question 16.
ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜର ସମକୋଣ ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 12ସେ.ମି. ଓ 5 ସେ.ମି. । ଏହାର ବୃହତ୍ତମ ବାହୁକୁ ସ୍ଥିର ରଖ୍ ତା’ର ଚାରିପାଖରେ ତ୍ରିଭୁଜଟିକୁ ଘୂରାଇଲେ ଯେଉଁ କୋନ୍ ସୃଷ୍ଟି ହେବ, ଘନଫଳ ଏବଂ ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ‘π’ମାଧ୍ୟମରେ ପ୍ରକାଶ କର ।
Solution:
ମନେକର ABC ସମକୋଣୀ ତ୍ରିଭୁଜର AB = 12 ସେ.ମି. ଓ BC = 5 ସେ.ମି. |
∴ AC = \(\sqrt{\mathrm{AB}^2+\mathrm{BC}^2}\) = \(\sqrt{12^2+5^2}\)
= \(\sqrt{25+144}\) = \(\sqrt{169}\) = 13 ସେ.ମି.

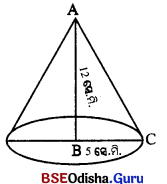
କ୍ଷୁଦ୍ରତମ ବାହୁ \(\overline{\mathrm{AB}}\) ର ଚତୁର୍ଦ୍ଦିଗରେ ଘୂରାଇଲେ ଯେଉଁ କୋଟି ଉତ୍ପନ୍ନ ହେବ ତାହାର ଆଧାରର ବ୍ୟାସାର୍ଦ୍ଧ BC ହେବ ।
∴ ଏହାର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ଆଧାରର କ୍ଷେତ୍ରଫଳ + ବକ୍ରତଳର କ୍ଷେତ୍ରଫଳ
= π (BC)² + π. BC . AC = π. BC (BC + AC) = π × 5 × 18 = 90π ଦଗ ସେ.ମି.|
ଆୟତନ = \(\frac { 1 }{ 3 }\) π (BC)² × AB = \(\frac { 1 }{ 3 }\) π. 5² . 12 = 100π ଦଗ ସେ.ମି.|