Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 6 ଅଙ୍କନ Ex 6(a) Textbook Exercise Questions and Answers.
BSE Odisha Class 10 Maths Solutions Geometry Chapter 6 ଅଙ୍କନ Ex 6(a)
Question 1.
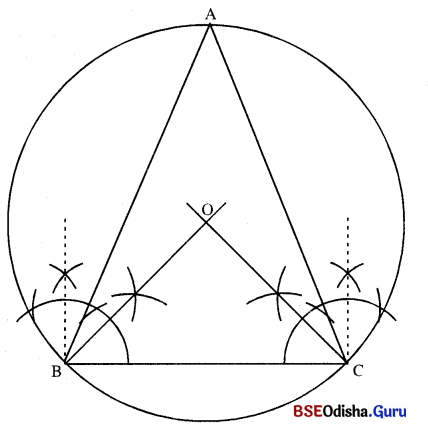
△ABC ରେ BC = 6 ସେ.ମି., m∠A = 45°, ତ୍ରକୁକର ପରିବର ଅନନ କର |
Solution:
(i) BC = 6 ସେ.ମି. ଏବଂ m∠OBC = m∠OCB = 90° – 45° = 45° ନେଇ AOBC ଅଙ୍କନ କର ।
(ii) ଠିକୁ କେନ୍ଦ୍ର ଏବଂ OB (କିମ୍ବା OC)କୁ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ବୃତ୍ତ ଅଙ୍କନ କର ।
(iii) ବୃତ୍ତ ଉପରିସ୍ଥ A ଯେକୌଣସି ଏକ ବିନ୍ଦୁ ନିଅ ଯେପରିକି BC ର ଏକ ପାର୍ଶ୍ଵ ରେ O ଏବଂ A ବିନ୍ଦୁ ମାନ ଅବସ୍ଥାନ କରିବେ ।
Question 2.
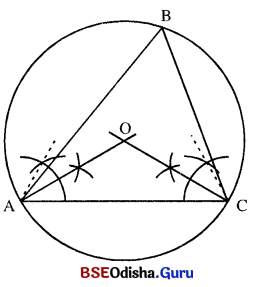
△ABC ରେ AC = 7 ସେ.ମି., m∠B = 60°, ତ୍ରକୁକର ପରିବର ଅନନ କର |
Solution:
(i) AC = 7 ସେ.ମି. ଏବଂ m∠OAC = m∠OCA = 90° – 60° = 30° ନେଇ △OAC ଅଙ୍କନ କର ।
(ii) O କୁ କେନ୍ଦ୍ର ଏବଂ \(\overline{\mathrm{OA}})\) (କିମ୍ବା \(\overline{\mathrm{OC}})\)) କୁ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ବୃତ୍ତ ଅଙ୍କନ କର ।
(iii) ବୃତ୍ତ ଉପରିସ୍ଥ B ଏପରି ଏକ ବିନ୍ଦୁ ନିଅ ଯେପରିକି \(\overline{\mathrm{AC}})\) ର ଏକ ପାର୍ଶ୍ଵରେ O ଏବଂ B ଅବସ୍ଥାନ କରିବ । △ABC ସମ୍ପୂର୍ଣ୍ଣ କର ।
![]()
Question 3.
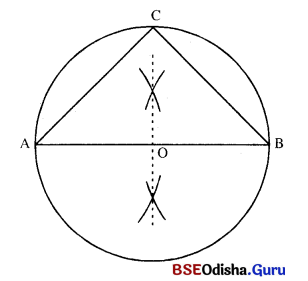
△ABC ରେ AB = 6.5 ସେ.ମି., m∠C= 90°, ତ୍ରକୁକର ପରିବର ଅନନ କର |
Solution:
(i) AB ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 6-5 ସେ.ମି. ।
(ii) AB ର ମଧ୍ୟବିନ୍ଦୁ O ନିର୍ଣ୍ଣୟ କର ।
(iii) Oକୁ କେନ୍ଦ୍ର ଏବଂ \(\overline{\mathrm{OA}})\) ବା \(\overline{\mathrm{OB}})\) କୁ ବ୍ୟାସାର୍ବନେଇ ଗୋଟିଏ ବୃତ୍ତ ଅଙ୍କନ କର ।
(iv) ବୃତ୍ତ ଉପରିସ୍ଥ ଯେକୌଣସି ଏକ ବିନ୍ଦୁ C ନେଇ △ABC ସମ୍ପୂର୍ଣ୍ଣ କର ।
Question 4.
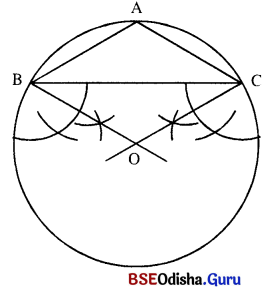
△ABC ରେ m∠A = 120°, BC = 4.5 ସେ.ମି. | ତ୍ରକୁକର ପରିବର ଅନନ କର |
(i) BC= 4.5 ସେ.ମି. ଏବଂ ∠OBC = ∠OCB = 120° – 90° = 30° ନେଇ △OBC ଅଙ୍କନ କର ।
(ii) O କୁ କେନ୍ଦ୍ର ଏବଂ OB (କିମ୍ବା OC)କୁ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ପରିବୃତ୍ତ ଅଙ୍କନ କର ।
(iii) ବୃତ୍ତ ଉପରିସ୍ଥ A ଏପରି ଏକ ବିନ୍ଦୁ ନିଅ ଯେପରିକି BC ର ବିପରୀତ ପାର୍ଶ୍ବରେ O ଏବଂ A ବିନ୍ଦୁମାନ ଅବସ୍ଥାନ କରିବେ ।
(iv) △ABC ସମ୍ପୂର୍ଣ କର ।
Question 5.
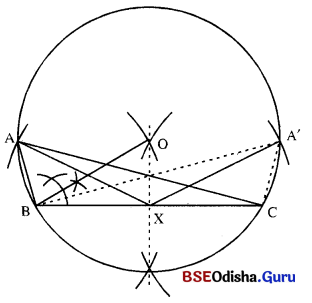
△ABC ରେ BC = 7 ସେ.ମି., m∠A = 60, AX ମଧ୍ୟମା = 4.5 68. ., ସେ.ମି., ପରିବର ଅନନ କର |
Solution:
(i) BC ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 7 ସେ.ମି. ।
(ii) B ବିନ୍ଦୁରେ 90° – m∠A = 30° ପରିମାଣ ବିଶିଷ୍ଟ ∠OBC ଅଙ୍କନ କର ।
(iii) \(\overline{\mathrm{BC}})\) ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ ଅଙ୍କନ କର, ଯାହାର \(\overrightarrow{\mathrm{BO}}\) କୁ O ବିନ୍ଦୁରେ ଛେଦକରୁ |
(iv) O କୁ କେନ୍ଦ୍ରକରି ଏବଂ OB ପରିମିତ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଏକ ବୃତ୍ତ ଅଙ୍କନ କର ।
(v) ‘X’ କୁ କେନ୍ଦ୍ର କରି XA ( = 4.5 ସେ.ମି.)ପରିମିତ ବ୍ୟାସାର୍ଥବିଶିଷ୍ଟ ଚାପ ବୃତ୍ତକୁ A ଓ A’ ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(vi) \(\overline{\mathrm{AB}})\) ଓ \(\overline{\mathrm{AC}})\) ଅଙ୍କନ କରି △ABC ବା A’BC ସମ୍ପୂର୍ଣ୍ଣ କର ।
Question 6.
△ABC ରେ ∠B ସମକୋଣ । AC = 7 ସେ.ମି., B ବିନ୍ଦୁରୁ \(\overline{\mathrm{AC}})\) ପ୍ରତିଲମ୍ବ । \(\overline{\mathrm{BD}})\) ର ଦୈର୍ଘ୍ୟ 3 ସେ.ମି. । ତ୍ରିଭୁଜଟି ଅଙ୍କନ କର । ଏ କ୍ଷେତ୍ରରେ \(\overline{\mathrm{AC}})\) ର ଏକ ପାର୍ଶ୍ବରେ B ବିନ୍ଦୁର କେତେ ଗୋଟି ଅବସ୍ଥିତି ପାଇଲ ?
Solution:
(i) \(\overline{\mathrm{AC}})\) ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 7 ସେ.ମି. |
(ii) AC ର ମଧ୍ୟବିନ୍ଦୁ O ଚିହ୍ନଟ କର । O କୁ କେନ୍ଦ୍ର ଏବଂ \(\overline{\mathrm{OA}})\) ବା \(\overline{\mathrm{OC}})\) କୁ ବ୍ୟାସାର୍ଷ ନେଇ ଅର୍ଥବୃତ୍ତ ଅଙ୍କନ କର ।
(iii) A ବିନ୍ଦୁରେ \(\overline{\mathrm{AC}})\) ପ୍ରତି \(\overline{\mathrm{AM}})\) କତ୍ମ ଅଙ୍କନ କରି, AM = BD = 3 ସେ.ମି. ଅଂଶ ଛେଦନ କର ।
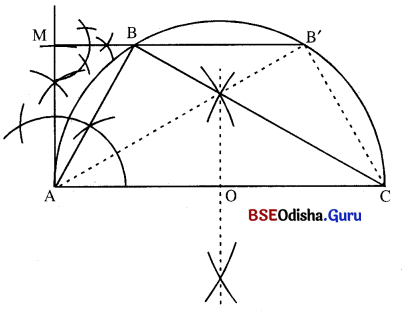
(iv) M ବିନ୍ଦୁରେ \(\overline{\mathrm{AC}})\) ସହ ସମାନ୍ତର କରି ଏକ ସରଳରେଖା ଅଙ୍କନ କର ତାହା ଅର୍ଥବୃତ୍ତକୁ B ଏବଂ B’ ବିନ୍ଦୁରେ ଛେଦକରିବ ।
(v) \(\overline{\mathrm{BA}})\) ଓ \(\overline{\mathrm{BC}})\) ଅଙ୍କନ କରି △ABC ଏବଂ B’A ଓ B’C ଅଙ୍କନ କରି △AB’C ସମ୍ପୁର୍ଣ୍ଣ କର ।
(ଏ କ୍ଷେତ୍ରରେ \(\overline{\mathrm{AC}})\) ର ଏକ ପାର୍ଶ୍ଵରେ B ବିନ୍ଦୁର ଦୁଇଗୋଟି ଅବସ୍ଥିତି ପାଇବ ।)
![]()
Question 7.
△ABC ରେ BC = 8 ସେ.ମି., m∠A = 45°, AD ଭଲତା 3 ସେ.ମି. ହେଲେ ପରିବର ଅନନ କର |
Solution:
(i) BC = 8 ସେ.ମି. ଏବଂ m∠OBC = m∠OCB =90° – 45° = 45° ନେଇ △OBC ଅଙ୍କନ କର ।
(ii) Oକୁ କେନ୍ଦ୍ର ଏବଂ \(\overline{\mathrm{OB}})\) (କିମ୍ବା \(\overline{\mathrm{OC}})\)୯କୁ) ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ବୃତ୍ତ ଅଙ୍କନ କର ।
(iii) B ବିନ୍ଦୁରେ 90° ପରିମାଣ ବିଶିଷ୍ଟ କୋଣ ଅଙ୍କନ କରି, BM = AD = 3 ସେ.ମି. ଅଂଶ ଛେଦନ କର |
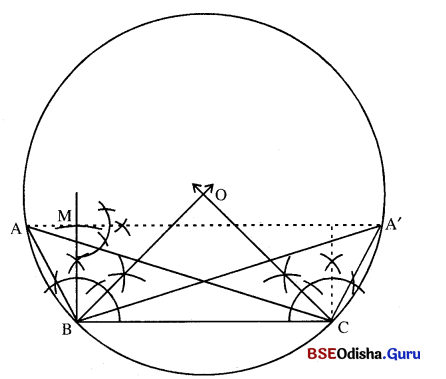
(iv) M ବିନ୍ଦୁରେ \(\overline{\mathrm{BC}})\) ସହ ସମାନ୍ତର କରି ଏକ ସରଳରେଖା ଅଙ୍କନ କର ଯାହା ବୃତ୍ତକୁ A ଓ A’ ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(v) \(\overline{\mathrm{AB}})\) ଓ \(\overline{\mathrm{AC}})\) ଅଙ୍କନ କରି △ABC ଏବଂ \(\mathrm{A}^{\prime} \mathrm{B}\) ଓ \mathrm{A}^{\prime} \mathrm{C} ଅଙ୍କନ କରି △A’BC ସମ୍ପୂର୍ଣ୍ଣ କର ।
Question 8.
△ABC ଅଙ୍କନ କର ଯାହାର m∠B = 60°, AC = 6.5 ସେ.ମି. ଏବଂ \(\overline{\mathrm{AX}})\) ମଧ୍ଯମାର ଦୈର୍ଘ୍ୟ = 5 ସେ.ମି. |
Solution:
(i) \(\overline{\mathrm{AC}})\) ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 6.5 ସେ.ମି. ।
(ii) \(\overline{\mathrm{AC}})\) ର ମଧ୍ୟବିନ୍ଦୁ D ଚିହ୍ନଟ କର ।
(iii) D ବିନ୍ଦୁରେ m∠YDC = 30° ଅଙ୍କନ କର ।
\(\overline{\mathrm{DC}})\) ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ ଅଙ୍କନ କର ଓ ତାହା \(\overrightarrow{\mathrm{DY}}\) କୁ O ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(iv) O କୁ କେନ୍ଦ୍ରକରି \(\overline{\mathrm{OD}})\) ପରିମିତ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଏକ ବୃତ୍ତ ଅଙ୍କନ କର ।
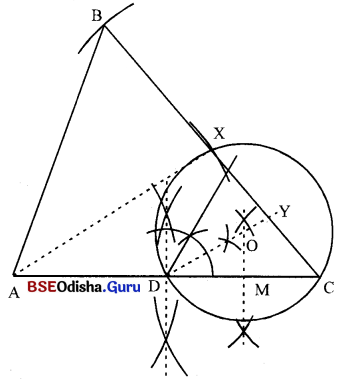
(v) Aକୁ କେନ୍ଦ୍ରକରି \(\overline{\mathrm{AX}})\) ବ୍ୟାସାର୍ଦ୍ଧ ପରିମିତ ଚାପ ପରିବୃତ୍ତକୁ X ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(vi) \(\overrightarrow{\mathrm{CX}}\) ରେଖା ଉପରେ B ଏପରି ଏକ ବିନ୍ଦୁ ନିଅ ଯୋଗକରି BX = CX ଏବଂ C – X – B ହେବ ।
(vii) B, A କୁ ଯୋଗକରି △ABC ସମ୍ପୂର୍ଣ୍ଣ କର ।
Question 9.
△ABC m∠A = 60°, BC = 7 ସେ.ମି., \(\overline{\mathrm{BE}})\) ⊥ \(\overline{\mathrm{AC}})\), BE = 6.3 ସେ.ମି. ଛେଦନ ଅନନ କର |
Solution:
(i) \(\overline{\mathrm{BC}})\) ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 7 ସେ.ମି. |
(ii) \(\overline{\mathrm{BC}})\) କୁ ଭୂମି ଏବଂ ଶୀର୍ଷକୋଣର ପରିମାଣ 60° ନେଇ ପରିବୃତ୍ତ ଅଙ୍କନ କର ।
(iii) \(\overline{\mathrm{BC}})\) କୁ ବ୍ୟାସ ନେଇ ଏକ ଅଦ୍ଧବୃତ୍ତ ଅଙ୍କନ କର ।
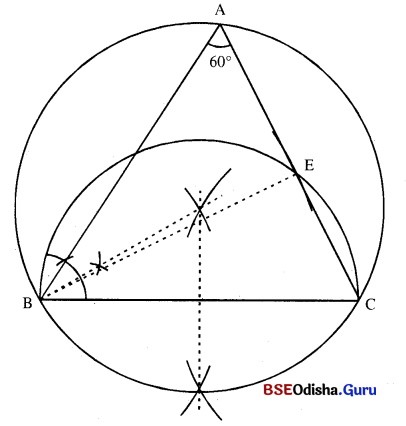
(iv) Bକୁ କେନ୍ଦ୍ରକରି \(\overline{\mathrm{BE}})\) ପରିମିତ ବ୍ୟାସାର୍କ୍ (6-3 ସେ.ମି.) ବିଶିଷ୍ଟ ଚାପ ଅର୍ଥବୃତ୍ତକୁ E ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(v) \(\overrightarrow{\mathrm{CE}}\), ଅଙ୍କନ ପରିବୃତ୍ତ A ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(vi) \(\overline{\mathrm{AB}})\) ଅଙ୍କନ କରି △ABC ସମ୍ପୂର୍ଣ୍ଣ କର ।
![]()
Question 10.
△ABC ର m∠A =150°, BC = 5 ସେ.ମି., AD ଉଳତା = 3 ସେ.ମି. ତ୍ରକୁକର ପରିବର ଅନନ କର |
Solution:
(i) BC = 5 ସେ.ମି., m∠OBC = 150°- 90° = 60° ନେଇ △OBC ଅଙ୍କନ କର ।
(ii) Oକୁ କେନ୍ଦ୍ର ଏବଂ (\(\overline{\mathrm{OB}})\) କିମ୍ବା \(\overline{\mathrm{OC}})\))କୁ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ବୃତ୍ତ ଅଙ୍କନ କର ।
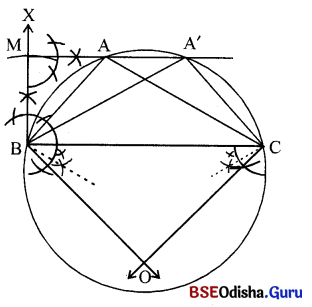
(iii) B ବିନ୍ଦୁରେ \(\overline{\mathrm{BC}})\) ପତି \(\overline{\mathrm{BX}})\) ବୃତ୍ତ ଅଙ୍କନ କର ସେଥୁରୁ BM = AD = 3 ସେ.ମି. ଅଂଶ ଛେଦନ କର ।
(iv) M ବିନ୍ଦୁରେ \(\overline{\mathrm{BC}})\) ସହ ସମାନ୍ତର କରି ଏକ ସରଳରେଖା ଅଙ୍କନ କର ଯାହା ବୃତ୍ତକୁ À ଓ A’ ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(v) AB, AC ଅଙ୍କନ କରି △ABC ଏବଂ \(\mathrm{A}^{\prime} \mathrm{B}\) ଓ \(\mathrm{A}^{\prime} \mathrm{C}\) ଅଙ୍କନ କରି △A’BC ସମ୍ପୂର୍ଣ କର ।
Question 11.
△ABC ନର m∠A = 60°, b : c = 2 : 3, BC = 7 ସେ.ମି. | ତ୍ରକୁକର ଅନନ କର |
Solution:
(i) \(\overline{\mathrm{BC}})\) ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 7 ସେ.ମି. |
(ii) \(\overline{\mathrm{BC}})\) କୁ ଭୂମି ଏବଂ ∠Aର ପରିମାଣ 60° ନେଇ ଏକ ପରିବୃତ୍ତ ଅଙ୍କନ କର ।
(iii) \(\overline{\mathrm{BC}})\) କୁ 3 : 2 ଅନୁପାତରେ P ବିନ୍ଦୁରେ ଅନ୍ତର୍ବିଭକ୍ତ କର ।
(iv) \(\overline{\mathrm{BC}})\) ର ସମଦ୍ଵିଖଣ୍ଡକ ଲମ୍ବ ବୃତ୍ତକୁ S ବିନ୍ଦୁରେ ଛେଦକରୁ ।
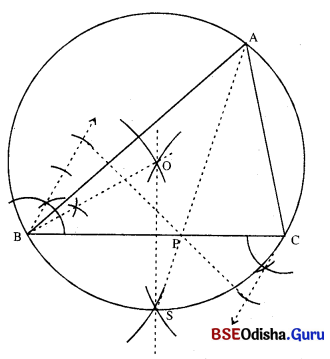
(v) \(\overrightarrow{\mathrm{SP}}\) ଅଙ୍କିତ ପରିବୃତ୍ତକୁ A ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(vi) \(\overline{\mathrm{AB}})\) ଓ \(\overline{\mathrm{AC}})\) ଅଙ୍କନ କରି △ABC ସମ୍ପୂର୍ଣ କର ।
Question 12.
ABCD ସାମାନ୍ତରିକ ଚିତ୍ର ଅଙ୍କନ କର ଯାହାର AB = 5.5 ସେ.ମି., କଣ୍ଠ \(\overline{\mathrm{BD}})\) ର ଦୈର୍ଘ୍ୟ = 8 ସେ.ମି. ଓ m∠DAC = 60° |
(i) \(\overline{\mathrm{DC}})\) ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 5-5 ସେ.ମି. ।
(ii) \(\overline{\mathrm{DC}})\) କୁ ସମଦ୍ବିଖଣ୍ଡକ କରି M ବିନ୍ଦୁ ନିର୍ଣ୍ଣୟ କର ।
(iii) \(\overline{\mathrm{MC}})\) କୁ ଭୂମି ଏବଂ 30° ଭୂମି ସଂଲଗ୍ନ କୋଣର ପରିମାଣ ନେଇ ଏକ ପରିବୃତ୍ତ ଅଙ୍କନ କର ।
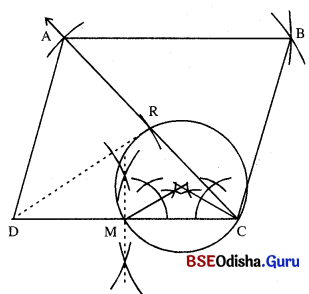
(iv) D କୁ କେନ୍ଦ୍ର କରି DR (4 ସେ.ମି. ) ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଚାପ ଅଙ୍କିତ ପରିବୃତ୍ତକୁ R ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(v) \(\overrightarrow{\mathrm{CR}}\) ଉପରିସ୍ଥ A ଏକ ବିନ୍ଦୁ ଯେପରିକି CR = AR ହେବ । \(\overline{\mathrm{AD}})\) ଅଙ୍କନ କର ।
(vi) ବର୍ତ୍ତମାନ A ଏବଂ C କୁ କେନ୍ଦ୍ରକରି ଯଥାକ୍ରମେ \(\overline{\mathrm{AB}})\) ଏବଂ \(\overline{\mathrm{AD}})\) ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଦୁଇଟି ଚାପ ଅଙ୍କନ କର ଯେପରି ସେମାନେ ପରସ୍ପରକୁ B ବିନ୍ଦୁରେ ଛେଦ କରିବେ ।
(vii) \(\overline{\mathrm{AB}})\) ଓ \(\overline{\mathrm{BC}})\) ଅଙ୍କନ କରି ABCD ସାମାନ୍ତରିକ ଚିତ୍ର ସମ୍ପୂର୍ଣ କର ।
