BSE Odisha 10th Class Maths Solutions Geometry Chapter 6 ଅଙ୍କନ Ex 6(d)

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 6 ଅଙ୍କନ Ex 6(d) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 6 ଅଙ୍କନ Ex 6(d)

Question 1.
(i) 6.5 ସେ.ମି. ଦୀର୍ଘ $\overline{\mathrm{AB}})$ ଅଙ୍କନ କରି ଏହାର ମଧ୍ୟବିନ୍ଦୁର ଅବସ୍ଥାନ ନିରୂପଣ କର ।
Solution:
(a) 6.5 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ $\overline{\mathrm{AB}})$ ଅଙ୍କନ କର ।
(b) $\overline{\mathrm{AB}})$ ର A ଓ B ଠାରେ ଯଥାକ୍ରମେ $\overrightarrow{\mathrm{AX}}$ ଓ $\overrightarrow{\mathrm{BY}}$ ରଶ୍ମି ଅଙ୍କନ କର, ଯେପରି X ଓ Y $\overline{\mathrm{AB}})$ ର ବିପରୀତ ପାର୍ଶ୍ବରେ ରହିବେ ଏବଂ m∠BAX = m∠ABY ହେବ । ଫଳରେ $\overrightarrow{\mathrm{AX}}$ || $\overrightarrow{\mathrm{BY}}$ |

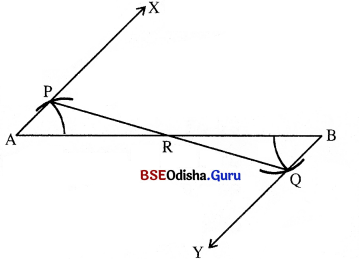
(c) କୁ କେନ୍ଦ୍ର ଓ ଏକ ସୁବିଧାଜନକ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଏକ ଚାପ ଅଙ୍କନ କର ଓ ଏହି ଚାପ ଯେଉଁ ବିନ୍ଦୁରେ $\overrightarrow{\mathrm{AX}}$ କୁ ଛେଦକରିବ ତା’ର ନାମ P ଦିଅ ।
(d) Bକୁ କେନ୍ଦ୍ର ଓ ପୂର୍ବୋକ୍ତ ପରିମିତ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଏକ ଚାପ ଅଙ୍କନ କର ଓ ଏହି ଚାପ ଯେଉଁ ବିନ୍ଦୁରେ $\overrightarrow{\mathrm{BY}}$କୁ ଛେଦ କରିବ ତା’ର ନାମ Q ଦିଅ ।

(e) $\overline{\mathrm{PQ}})$ ଅଙ୍କନ କର ଓ ତାହା ଯେଉଁ ବିନ୍ଦୁରେ $\overline{\mathrm{AB}})$ କୁ ଛେଦକରିବ ତା’ର ନାମ R ଦିଅ । ବର୍ତ୍ତମାନ R, $\overline{\mathrm{AB}})$ ର ମଧ୍ୟବିନ୍ଦୁ ।
[ବି.ଦ୍ର. $\overline{\mathrm{AB}})$ ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ ଅଙ୍କନ କରି ‘R’ ବିନ୍ଦୁ ଚିହ୍ନଟ କରାଯାଇପାରିବ ।

(ii) 76 ସେ.ମି. ଦୀର୍ଘ $\overline{\mathrm{PQ}})$ ଅଙ୍କନ କରି ଏହାକୁ 4 ସମାନ ଭାଗ କର ।
Solution:
(a) 76 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ $\overline{\mathrm{PQ}})$ ଅଙ୍କନ କର ।
(b) $\overline{\mathrm{PQ}})$ ର P ଓ Q ଠାରେ ଯଥାକ୍ରମେ $\overrightarrow{\mathrm{PX}}$ ଓ $\overrightarrow{\mathrm{QY}}$ ରଶ୍ମି ଅଙ୍କନ କର,
ଯେପରି X ଓ Y, $\overline{\mathrm{PQ}})$ ର ବିପରୀତ ପାର୍ଶ୍ଵରେ ରହିବେ ଏବଂ m∠QPX = m∠PQY ହେବ । ଫଳରେ
$\overrightarrow{\mathrm{PX}}$ || $\overrightarrow{\mathrm{QY}}$ ହେବ |
(c)P କୁ କେନ୍ଦ୍ର ଓ ଏକ ସୁବିଧାଜନକ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଏକ ଚାପ ଅଙ୍କନ କର ଓ ଏହି ଚାପ ଯେଉଁ ବିନ୍ଦୁରେ $\overrightarrow{\mathrm{PX}}$ କୁ ଛେଦକରିବ ତା’ର ନାମ A₁ ଦିଅ ।
$\overrightarrow{\mathrm{PX}}$ ଉପରେ A₂ ଓ A₃ ଚିହ୍ନଟ କର ଯେପରି PA₁ = A₁A₂ = A₂A₃ |

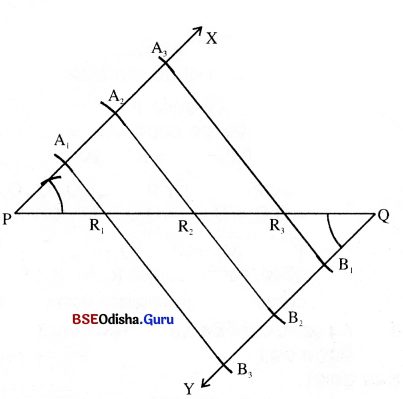
(d) ପୂର୍ବୋକ୍ତ ପ୍ରଣାଳୀ ଅବଲମ୍ବନ କରି $\overrightarrow{\mathrm{QY}}$ ଉପରେ B₁, B₂, B₃ ବିନ୍ଦୁ ତିନୋଟି ଚିହ୍ନଟ କର ଯେପରି PA₁ = QB₁ = B₁B₂ = B₂B₃ ।
(e) $\overleftrightarrow{\mathrm{A}_3 \mathrm{~B}_1}, \overleftrightarrow{\mathrm{A}_2 \mathrm{~B}_2}, \overleftrightarrow{\mathrm{A}_1 \mathrm{~B}_3}$ ଅଙ୍କନ କର ଓ ଯେଉଁ ବିନ୍ଦୁରେ ଉକ୍ତ ରେଖାମାନ $\overline{\mathrm{PQ}})$ କୁ ଛେଦ କରିବେ ସେଗୁଡ଼ିକୁ ଯଥାକ୍ରମେ R₁, R₂ ଓ R₃ ଭାବେ ନାମିତ କର ।
ବର୍ତ୍ତମାନ $\overline{\mathrm{PQ}})$ ସମାନ ଚାରିଭାଗରେ ବିଭକ୍ତ ହୋଇପାରିଲା ।
[ବି.ଦ୍ର. $\overline{\mathrm{PQ}})$ ର ସମଦ୍ଵିଖଣ୍ଡକ ଲମ୍ବ ଅଙ୍କନ ଦ୍ବାରା R₂ ଚିହ୍ନଟ କରାଯାଇ ପାରିବ । ତତ୍ପରେ $\overline{\mathrm{PR}_2}$ ଓ $\overline{\mathrm{R}_2 \mathrm{Q}}$ ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ ଅଙ୍କନ କରାଇ ଯଥାକ୍ରମେ R₁ ଓ R₃ ଚିହ୍ନଟ କରାଯାଇ ପାରିବ, ଯାହାଦ୍ଵାରା $\overline{\mathrm{PQ}})$ ସମାନ ଚାରିଭାଗରେ ବିଭକ୍ତ ହୋ ଆରିବ ।]

Question 2.
7-2 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଏକ ରେଖାକୁ ସମାନ 6 ଭାଗ କର ।
Solution:
(a) 7.2 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ $\overline{\mathrm{AB}})$ ଅଙ୍କନ କର ।
(b) $\overline{\mathrm{AB}})$ ର A ଓ B ଠାରେ ଯଥାକ୍ରମେ $\overrightarrow{\mathrm{AX}}$ ଓ $\overrightarrow{\mathrm{BY}}$ ରଶ୍ମି ଅଙ୍କନ କର, ଯେପରି X ଓ Y, $\overline{\mathrm{AB}})$ର ବିପରୀତ ପାର୍ଶ୍ବରେ ରହିବେ ଏବଂ m∠BAX = m∠ABY ହେବ ।
ଫଳରେ $\overrightarrow{\mathrm{AX}}$ || $\overrightarrow{\mathrm{BY}}$ |
(c) A କୁ କେନ୍ଦ୍ର ଓ ଏକ ସୁବିଧାଜନକ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଏକ ଚାପ ଅଙ୍କନ କର ଓ ଏହି ଚାପ ଯେଉଁ ବିନ୍ଦୁରେ $\overrightarrow{\mathrm{AX}}$ କୁ ଛେଦକରିବ ତାର ନାମ P₁ ଦିଅ । ଏହିପରି ଚାପ ଅଙ୍କନ ପ୍ରଣାଳୀରେ $\overrightarrow{\mathrm{AX}}$ ଉପରେ P₂, P₃, P₄ ବିନ୍ଦୁମାନ ଚିହ୍ନିତକର ସେପରି AP₁ = P₁P₂ = P₂P₃ = P₃P₄ = P₄P₅ ହେବ ।

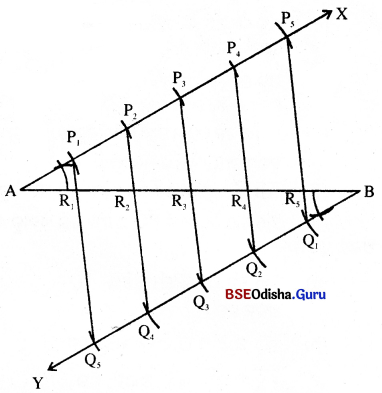
(d) ସୋପାନ (iii)ପରି BY ଉପରେ Q₁, Q₂, Q₃, Q₄ ଓ Q₅ ବିନ୍ଦୁମାନ ଚିହ୍ନଟ କର, ଯେପରି BQ₁ = Q₁Q₂ = Q₃Q₄ = Q₄Q₅ = AP₁ ହେବ ।
(e) $\stackrel{\leftrightarrow}{\mathrm{P}_5 \mathrm{Q}_1}, \stackrel{\leftarrow}{\mathrm{P}_4 \mathrm{Q}_2}, \stackrel{\leftarrow}{\mathrm{P}_3 \mathrm{Q}_3}, \stackrel{\leftarrow}{\mathrm{P}_2 \mathrm{Q}_4}, \stackrel{\leftarrow}{\mathrm{P}_1 \mathrm{Q}_5}$ ଅଙ୍କନ କର ଓ ଯେଉଁ ବିନ୍ଦୁରେ ଉକ୍ତ ରେଖାମାନ $\overline{\mathrm{AB}})$ କୁ ଛେଦ କରିବେ, ସେଗୁଡ଼ିକୁ ଯଥାକ୍ରମେ R₁, R₂, R₃, R₄, ଓ R₅ ଭାବେ ନାମିତ କର । ବର୍ତ୍ତମାନ $\overline{\mathrm{AB}})$ ସମାନ ଛଅଭାଗରେ ବିଭକ୍ତ ହୋଇପାରିଲା ।

Question 3.
64 ସେ.ମି. ଦୀର୍ଘ ବିଶିଷ୍ଟ $\overline{\mathrm{AB}})$ ଅଙ୍କନ କରି ଏହାକୁ 3 : 2 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭାଜନ କରୁଥ‌ିବା ବିନ୍ଦୁର ଅବସ୍ଥାନ ନିରୂପଣ କର ।
Solution:
(a) 64 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ରେଖାଖଣ୍ଡ $\overline{\mathrm{AB}})$ ଅଙ୍କନ କର ।
(b) $\overline{\mathrm{AB}})$ ର A ଓ B ବିନ୍ଦୁଠାରେ ଯଥାକ୍ରମେ $\overrightarrow{\mathrm{AX}}$ ଓ $\overrightarrow{\mathrm{BY}}$ ରଶ୍ମି ଅଙ୍କନ କର ଯେପରି X ଓ Y, $\overline{\mathrm{AB}})$ ର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥାନ କରିବେ ଓ m∠XAB m∠ABY ହେବ ।

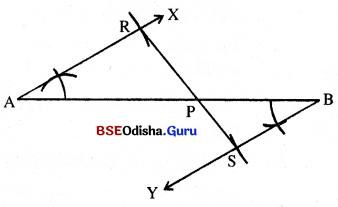
ଫଳରେ $\overrightarrow{\mathrm{AX}}$ || $\overrightarrow{\mathrm{BY}}$ |
(c) $\overrightarrow{\mathrm{AX}}$ ଉପରେ R ଓ $\overrightarrow{\mathrm{BY}}$ ଉପରେ S ଚିହ୍ନଟ କର, ଯେପରି AR = 3 ସେ.ମି. ଓ BS = 2 ସେ.ମି. ହେବ ।
(d) $\overleftrightarrow{\mathrm{RS}}$ ଅଙ୍କନ କର ।
(e) $\overleftrightarrow{\mathrm{RS}}$ ଓ $\overline{\mathrm{AB}})$ର ଛେଦବିନ୍ଦୁକୁ P ନାମ ଦିଅ । ବର୍ତ୍ତମାନ $\overline{\mathrm{AB}})$ ରେଖାଖଣ୍ଡ P ବିନ୍ଦୁରେ ଅନ୍ତର୍ବିଭାଜିତ ହେଲା ।

Question 4.
65 ସେ.ମି. ଦୀର୍ଘ $\overline{\mathrm{BC}})$ ଅଙ୍କନ କରି ଏହାକୁ 5 : 3 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭାଜନ ଓ ବହିର୍ବିଭାଜନ କରୁଥିବା ବିନ୍ଦୁଦ୍ଵୟ ନିରୁପଣ କର ।
Solution:

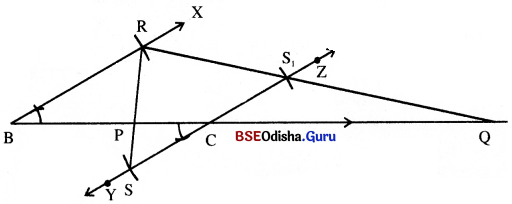
(a) 6.5 ସେ.ମି. ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ $\overline{\mathrm{BC}})$ ଅଙ୍କନ କର ।
(b) $\overline{\mathrm{BC}})$ ର B ଓ C ବିନ୍ଦୁଠାରେ ଯଥାକ୍ରମେ $\overrightarrow{\mathrm{BX}}$ ଓ $\overrightarrow{\mathrm{CY}}$ ରଶ୍ମି ଅଙ୍କନ କର ଯେପରି, X ଓ Y $\stackrel{\leftrightarrow}{\mathrm{BC}}$ ର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥାନ କରିବେ ଓ m∠XBC = m∠BCY ହେବ ।
(c) $\overrightarrow{\mathrm{BX}}$ ଉପରେ R ଓ $\overrightarrow{\mathrm{CY}}$ ଉପରେ S ଚିହ୍ନଟ କର, ଯେପରି BR = 5 ସେ.ମି. ଓ CS = 3 ସେ.ମି. ହେବ ।
(d) $\overleftrightarrow{\mathrm{RS}}$ ଅଙ୍କନ କର ତାହା $\overline{\mathrm{BC}})$ କୁ P ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(e) $\overrightarrow{\mathrm{CY}}$ ର ବିପରୀତ ରଶ୍ମି $\overrightarrow{\mathrm{CZ}}$ ଅଙ୍କନ କର ।
(f) $\overrightarrow{\mathrm{CZ}}$ ଉପରେ S₁ ବିନ୍ଦୁ ଚିହ୍ନଟ କର, ଯେପରି CS₁ = 3 ସେ.ମି. ହେବ ।
(g) $\overleftrightarrow{\mathrm{RS}}_1$ ଅଙ୍କନ କର ତାହା $\overline{\mathrm{BC}})$ କୁ Q ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
(h) ବରମାନ P ଓ Q, $\overline{\mathrm{BC}})$ ର ଯଥାକ୍ରମେ ଅନ୍ତେଜିଉନ୍ତ ଦନ୍ଦ୍ର ଏବଂ ବସ୍ତିବରକ୍ତ ବୁଦ୍ |
(i) ଏଠାରେ BP : PC : 5 : 3 ଏବଂ BQ : CQ = 5 : 3 |

Question 5.
7.5 ସେ.ମି. ଦୀର୍ଘ $\overline{\mathrm{PQ}})$ ଅଙ୍କନ କରି ଏହାକୁ ଦୁଇଟି ଅଂଶରେ ଭାଗ କର, ଯେପରିକି ସେମାନଙ୍କର ଦୈର୍ଘ୍ୟର ଅନୁପାତ 4 : 3 ହେବ । ଏକ ଆୟତଚିତ୍ର ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ଯଥାକ୍ରମେ $\overline{\mathrm{PQ}})$ ର ଦୁଇ ଅଂଶର ଦୈର୍ଘ୍ୟ ସହ ସମାନ ।
Solution:
(a) 7.5 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ $\overline{\mathrm{PQ}})$ ଅଙ୍କନ କର ।
(b) $\overline{\mathrm{PQ}})$ ର P ଓ Q ବିନ୍ଦୁଠାରେ ଯଥାକ୍ରମେ $\overrightarrow{\mathrm{PX}}$ ଓ $\overrightarrow{\mathrm{QY}}$ ରଶ୍ମି ଅଙ୍କନ କର
ଯେପରି X, Y ଓ $\stackrel{\leftrightarrow}{\mathrm{PQ}}$ ର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥାନ କରିବେ ଓ m∠XPQ = m∠PQY ହେବ ।
(c) $\overrightarrow{\mathrm{PX}}$ ଉପରେ R ଓ $\overrightarrow{\mathrm{QY}}$ ଉପରେ S ଚିହ୍ନଟ କର, ଯେପରି PR = 4 ସେ.ମି. ଓ QS = 3 ସେ.ମି. ହେବ ।

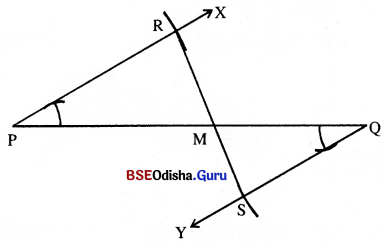
(d) $\overleftrightarrow{\mathrm{RS}}$ ଅଙ୍କନ କର ତାହା $\overleftrightarrow{\mathrm{PQ}}$ କୁ M ବିନ୍ଦୁରେ ଛେଦକରୁ । ବର୍ତ୍ତମାନ $\overline{\mathrm{PQ}}$ ରେଖାଖଣ୍ଡ M ବିନ୍ଦୁରେ ଅଳ୍ପବିକାକତ ହେଲା |

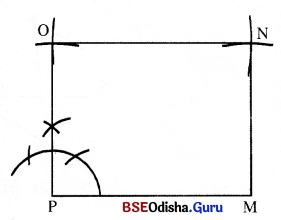
(e) PM କୁ ଦୈର୍ଘ୍ୟରୂପେ ଅଙ୍କନ କର ।
(f) P ବିନ୍ଦୁରେ ଲମ୍ବ ଅଙ୍କନ କରି $\overline{\mathrm{PO}})$ ଅଂଶ ଛେଦନ କର ଯେପରି PO = MQ |
(g) P କେନ୍ଦ୍ର ଓ PM ବ୍ୟାସାର୍ଦ୍ଧ ପରିମିତ ଚାପ ଏବଂ M କେନ୍ଦ୍ର ଓ OP ବ୍ୟାସାର୍ଦ୍ଧ ପରିମିତ ଚାପ ପରସ୍ପରକୁ N ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(h) ବର୍ତ୍ତମାନ PONM ଆବଶ୍ୟକୀୟ ଆୟତଚିତ୍ର ।

Question 6.
△ABCରେ BC = 6.5 ସେ.ମି., $\overline{\mathrm{BY}})$ ମଧ୍ଯମାର ଦୈର୍ଘ୍ୟ 6 ସେ.ମି. ଓ $\overline{\mathrm{CZ}})$ ମଧ୍ଯମାର ଦୈର୍ଘ୍ୟ 5.5 ସେ.ମି. । ତ୍ରିଭୁଜଟି ଅଙ୍କନ କର ।
Solution:
(a) $\overline{\mathrm{BC}})$ ରେଖାଖଣ୍ଡ ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 6.5 ସେ.ମି. ହେବ ।
(b) $\overline{\mathrm{BC}})$ ର ମଧ୍ୟବିନ୍ଦୁ D ନିରୂପଣ କର ଏବଂ $\overline{\mathrm{BC}})$ ରେଖା ଉପରେ X ଏପରି ଏକ ବିନ୍ଦୁ ନିଅ ଯେପରିକି CD = CX ହେବ ।

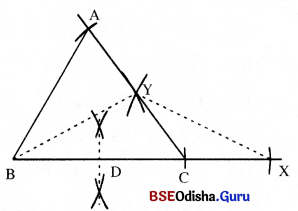
(c) B ଓ X କୁ କେନ୍ଦ୍ରକରି ଯଥାକ୍ରମେ 6 ସେ.ମି. ଓ 6.5 ସେ.ମି. ବ୍ୟାସାର୍କକୁ ନେଇ ଦୁଇଟି ଚାପ ଅଙ୍କନ କର ଯେପରିକି ସେମାନେ ପରସ୍ପରକୁ Y ବିନ୍ଦୁରେ ଛେଦ କରିବେ ।
(d) $\overrightarrow{\mathrm{CY}}$ ରେଖାଖଣ୍ଡ ଉପରେ A ଏପରି ଏକ ବିନ୍ଦୁ ଯେପରିକି CY = AY ହେବ ।
(e) A, B କୁ ଯୋଗକରି △ABC ସମ୍ପୂର୍ଣ୍ଣ କର ।