Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 6 ଅଙ୍କନ Ex 6(e) Textbook Exercise Questions and Answers.
BSE Odisha Class 10 Maths Solutions Geometry Chapter 6 ଅଙ୍କନ Ex 6(e)
Question 1.
△ABC ଅଙ୍କନ କର ଯାହାର BC = 6 ସେ.ମି., m∠BAC = 60 ଏବଂ \(\overline{\mathrm{AD}})\) ମଧ୍ଯମାର ଦୈର୍ଘ୍ୟ 4.5 ସେ.ମି. । △ABCର ଏକ ସଦୃଶ ତ୍ରିଭୁଜ 3.5 ସେ.ମି. ବ୍ୟାସାର୍କ ବିଶିଷ୍ଟ ବୃତ୍ତରେ ଅନ୍ତର୍ଲିଖନ କର ।
Solution:
(i) \(\overline{\mathrm{BC}})\) ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 6 ସେ.ମି. ।
(ii) \(\overline{\mathrm{BC}})\) ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ L ଅଙ୍କନ କର ଓ \(\overline{\mathrm{BC}})\) ର ମଧ୍ୟବିନ୍ଦୁର ନାମ D ଦିଅ ।
(iii) ∠PBC ଅଙ୍କନ କର ଯାହାର ପରିମାଣ 30° |
(iv) \( \overrightarrow{\mathrm{BP}}\) ଓ L ର ଛେଦବିନ୍ଦୁର ନାମ O ନିଅ ।
(v) Oକୁ କେନ୍ଦ୍ରକରି OB ପରିମିତ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଏକ ବୃତ୍ତ ଅଙ୍କନ କର ।
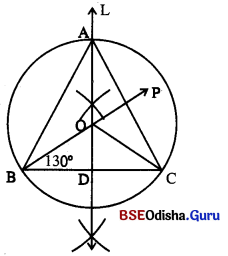
(vi) D ବିନ୍ଦୁରୁ 4.5 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଏକ ଚାପ ଅଙ୍କନ କର ଯାହା ଅଙ୍କିତ ବୃତ୍ତକୁ A ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
(vii) \(\overline{\mathrm{AB}})\) ଓ \(\overline{\mathrm{AC}})\) ଅଙ୍କନ କରି △ABCର ଅଙ୍କନ ଶେଷ କର ।
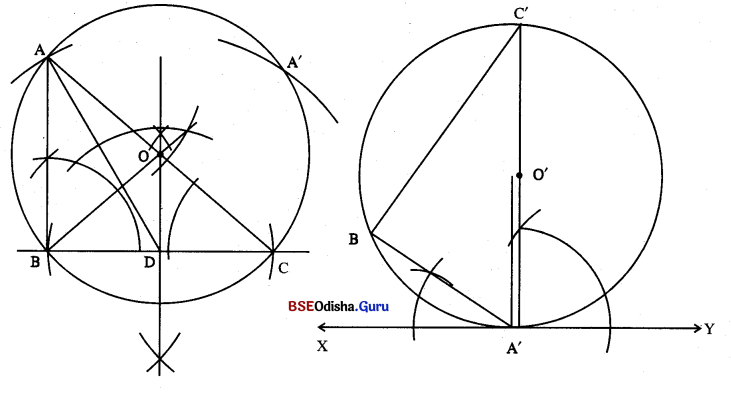
(viii) 3.5 ସେ.ମି. ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ଆଉ ଏକ ବୃତ୍ତ ଅଙ୍କନ କରି ବୃତ୍ତରେ ଏକ ବିନ୍ଦୁ A’ ନିଅ ଓ ଉକ୍ତ ବୃତ୍ତର କେନ୍ଦ୍ର O’ ନିଅ । \(\overline{\mathrm{O}^{\prime} \mathrm{A}^{\prime}}\) ଅଙ୍କନ କର ।
(ix) \(\overline{\mathrm{O}^{\prime} \mathrm{A}^{\prime}}\) ପ୍ରତି A’ ବିନ୍ଦୁରେ ଏକ ଲମ୍ବ ଅଙ୍କନ କରି ଏହାର ନାମ \(\stackrel{\leftrightarrow}{XY}\) ନିଅ ।
(x) ∠A’B’ ଅଙ୍କନ କର ଯାହାର ପରିମାଣ ∠ACBର ପରିମାଣ ସହ ସମାନ ହେବ ଓ B’ ବୃତ୍ତ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ ହେବ । ସେହିପରି ∠YA’C’ ଅଙ୍କନ କର ଯାହାର ପରିମାଣ ∠ABCର ପରିମାଣ ସହ ସମାନ ହେବ ଓ C’ ବୃତ୍ତ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ ହେବ ।
(xi) A’B’C’ ବିନ୍ଦୁରେ ଏକ ଲମ୍ବ ଅଙ୍କନ କରି ଏହାର ନାମ △ABC ~ △A’B’C’ |
![]()
Question 2.
△ABC ଅଙ୍କନ କର ଯାହାର BC = 6 ସେ.ମି., m∠B = 60 ଏବଂ \(\overline{\mathrm{AD}})\) ଲମ୍ବର ଦୈର୍ଘ୍ୟ 4.5 ସେ.ମି. । △ABCର ଏକ ସଦୃଶ ତ୍ରିଭୁଜ 2.5 ସେ.ମି. ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ବୃତ୍ତରେ ପରିଲିଖନ କର ।
Solution:
(i) L ରେଖା ଅଙ୍କନ କରି ଏହା ଉପରେ D ବିନ୍ଦୁ ଚିହ୍ନଟ କର ଏବଂ L ପ୍ରତି D ବିନ୍ଦୁରେ ଏକ ଲମ୍ବ \( \overrightarrow{\mathrm{DX}}\) ଅଙ୍କନ କର । \( \overrightarrow{\mathrm{DX}}\) ଉପରେ A ଏକ ବିନ୍ଦୁ ନିଅ ଯେପରି AD = 4.5 ସେ.ମି. ହେବ ।
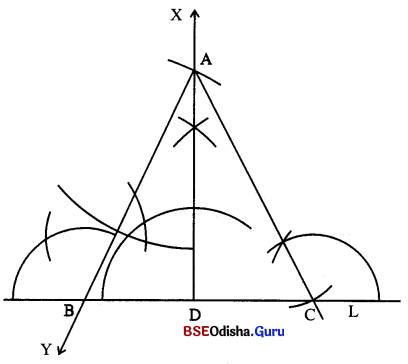
(ii) ∠DAY ଅଙ୍କନ କର ଯେପରି m∠DAY = 30°, \( \overrightarrow{\mathrm{AY}}\) ଓ L ରେଖାର ଛେଦବିନ୍ଦୁର ନାମ B ଦିଅ । B ବିନ୍ଦୁରୁ 6 ସେ.ମି. କର ଯାହା L କୁ C ବିନ୍ଦୁରେ ଛେଦ କରିବ । \(\overline{\mathrm{AC}})\) ଅଙ୍କନ କର ।
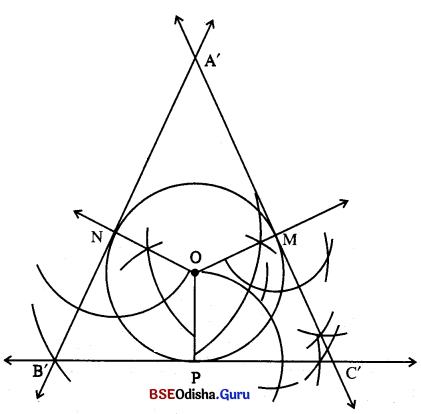
(iii) 2.5 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଆଉ O ନିଅ । \(\overline{\mathrm{OP}})\) ଏକ ବ୍ୟାସାର୍ଷ ଅଙ୍କନ କର ।
(iv) \(\overline{\mathrm{OM}})\) ଓ \(\overline{\mathrm{ON}})\) ବ୍ୟାସାର୍ଦ୍ଧ ଦ୍ଵୟ ଅଙ୍କନ କର ଯେପରି m∠MOP = ∠ACBର ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ଓ m∠PON = ∠ABCର ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ସହ ସମାନ ।
(v) M, N ଓ P ବିନ୍ଦୁରେ ବୃତ୍ତପ୍ରତି ସ୍ପର୍ଶକମାନ ଅଙ୍କନ କର ।
(vi) M ଓ N ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ ଦ୍ବୟର ଛେଦବିନ୍ଦୁ, N ଓ P ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକଦ୍ବୟର ଛେଦବିନ୍ଦୁ P ଓ M ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକଦ୍ବୟର ଛେଦବିନ୍ଦୁ ଯଥାକ୍ରମେ A’, B’ ଓ C’ ହେଉ ।
(vii) △ABC ~ △A’B’C’
Question 3.
କୌଣସି △XYZ ଅଙ୍କନ କର । △XYZ ର ସଦୃଶ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ଯାହାର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ, ଦତ୍ତ ତ୍ରିଭୁଜର ଅନୁରୂପ ବାହୁର ଦୁଇ-ତୃତୀୟାଂଶ ହେବ ।
Solution:
(i) ଯେକୌଣସି △XYZ ଅଙ୍କନ କର ।
(ii) △XYZର \(\overline{\mathrm{YZ}})\) କୁ 2 : 1 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରି Y’ ବିନ୍ଦୁ ଚିହ୍ନଟ କର ଯେପରି YY’ : Y’Z = 2 : 1 ହେବ ।
(iii) \(\overline{\mathrm{XZ}})\) ସହ ସମାନ୍ତର କରି Y’ ବିନ୍ଦୁରେ ଅଙ୍କିତ ରେଖା \(\overline{\mathrm{XY}})\) କୁ ଯେଉଁ ବିନ୍ଦୁରେ ଛେଦ କରିବ ତାହାର ନାମ X’ ଦିଅ ।
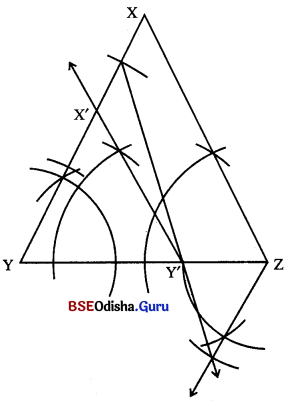
(iv) △X’YZ ~ △XYZ
Question 4.
△ABC ଅଙ୍କନ କର ଯାହାର BC = 5.7 ସେ.ମି., m∠B = 60 ଏବଂ \(\overline{\mathrm{BE}})\) ମଧ୍ଯମାର ଦୈର୍ଘ୍ୟ 4.8 ସେ.ମି. । ତ୍ରିଭୁଜଟି ଅଙ୍କନ କରି 2.3 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତରେ ପରିଲିଖନ କର । ବିଶ୍ଳେଷଣ ଚିତ୍ର :
Solution:
(i) \(\overline{\mathrm{BC}})\) ଅଙ୍କନ କର ଯେପରି BC = 5.7 ସେ.ମି. । \(\overline{\mathrm{BC}})\) ର ସମଦ୍ଵିଖଣ୍ଡକ ଲମ୍ବ ଅଙ୍କନକରି \(\overline{\mathrm{BC}})\) ର ମଧ୍ୟବିନ୍ଦୁ D ଚିହ୍ନଟ କର ।
(ii) BC ର D ବୃତ୍ତରେ ∠EDC ଅଜନ୍ କର ଯେପରି m∠EDC = 60° |
(iii) B କୁ କେନ୍ଦ୍ରକରି 4.8 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ଚାପ ଅଙ୍କନ କର ଓ ଚାପଟି \( \overrightarrow{\mathrm{DF}}\) କୁ ଯେଉଁ ବିନ୍ଦୁରେ ଛେଦ କରିବ ତା’ର ନାମ E ଦିଅ ।
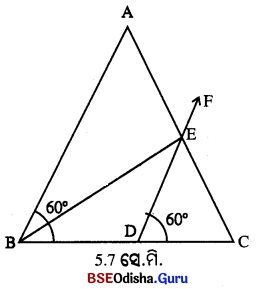
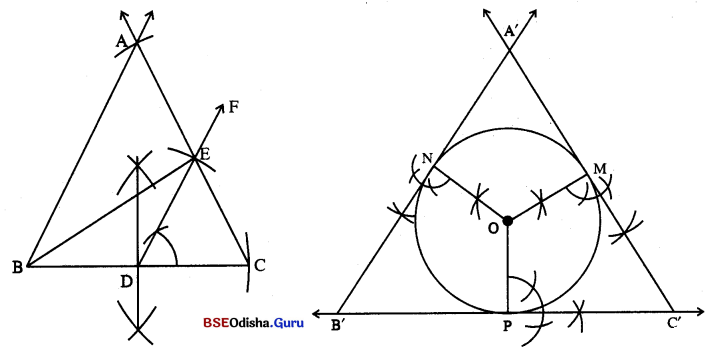
(iv) \( \overrightarrow{\mathrm{CE}}\) ଅଙ୍କନ କର ଓ \( \overrightarrow{\mathrm{CE}}\) ଉପରେ A ବିନ୍ଦୁ ଚିହ୍ନଟ କର ଯେପରି CE = EA ହେବ । \(\overline{\mathrm{AB}})\) ଅଙ୍କନ କର । △ABC ଆବଶ୍ୟକୀୟ ତ୍ରିଭୁଜ ।
(v) 2.3 ସେ.ମି. ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ବୃତ୍ତ ଅଙ୍କନ କରି 2 ନମ୍ବର ପରି ତ୍ରିଭୁଜ A’B’C’ ପରିଲିଖନ କର ।
![]()
Question 5.
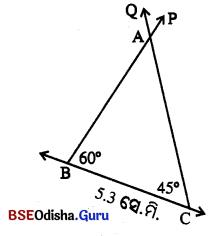
△ABC ଅଙ୍କନ କର ଯାହାର BC = 5.3 ସେ.ମି., m∠B = 60° ଏବଂ m∠C = 45° । 2.5 ସେ.ମି. ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତରେ △ABCର ଏକ ସଦୃଶ ତ୍ରିଭୁଜ ଅନ୍ତର୍ଲିଖନ କର ।
ବିଶ୍ଳେଷଣ ଚିତ୍ର :
Solution:
(i) \(\overline{\mathrm{BC}})\) ଅଙ୍କନ କର ଯେପରି BC = 5.3 ସେ.ମି. ।
(ii) ∠PBC ଅଙ୍କନ କର ଯେପରି m∠PBC = 60° |
(iii) \(\overline{\mathrm{BC}})\) ର ଯେଉଁ ପାର୍ଶ୍ବରେ P ଅବସ୍ଥିତ, ସେହି ପାର୍ଶ୍ବରେ ∠QCB ଅବସ୍ଥିତ, ସେହି ପାର୍ଶ୍ବରେ m∠QCB = 45° |
(iv) \( \overrightarrow{\mathrm{CQ}}\) ଓ \( \overrightarrow{\mathrm{BP}}\) ର ଛେଦବିନ୍ଦୁର ନାମ A ଦିଅ ।
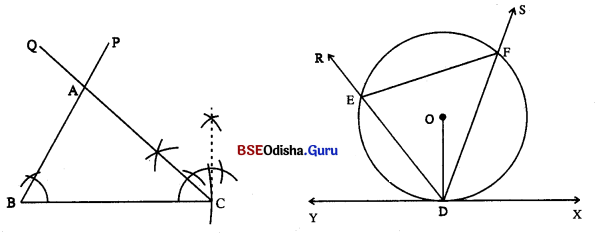
(v) 2.5 ସେ.ମି. ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତ ଅଙ୍କନ କରି କେନ୍ଦ୍ରର ନାମ O ଦିଅ । ଏକ ବ୍ୟାସାର୍ଦ୍ଧ \(\overline{\mathrm{OD}})\) ନିଅ ।
(vi) \(\overline{\mathrm{OD}})\) ପ୍ରତି D ବିନ୍ଦୁରେ \( \overrightarrow{\mathrm{DX}}\) ଲମ୍ବ ଅଙ୍କନ କରି \( \overrightarrow{\mathrm{XD}}\) ଉପରେ Y ଏକ ବିନ୍ଦୁ ନିଅ ।
(vii) \(\overline{\mathrm{YD}})\) ଉପରେ ∠YDR ଅଙ୍କନ କର ଯେପରି m∠YDR = m∠C = 45° ବୃତ୍ତକୁ E ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(viii) ସେହିପରି ∠XDS ଅଙ୍କନ କର ଯେପରି m∠XDS = m∠B = 60° ଓ \( \overrightarrow{\mathrm{DS}}\) ବୃତ୍ତକୁ F ବିନ୍ଦୁରେ ଛେଦକରୁ । \(\overline{\mathrm{YD}})\) ଅଙ୍କନ କର । △ABC ~ △DEF ।
Question 6.
△ABC ଅଙ୍କନ କର ଯାହାର BC = 7 ସେ.ମି., m∠B = 60° ଏବଂ b + c = 11.2 ସେ.ମି. । ତ୍ରିଭୁଜଟି ଅଙ୍କନ କରି ଏହାର ସଦୃଶକୋଣୀ ଏକ ତ୍ରିଭୁଜ 1.5 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତରେ ପରିଲିଖନ କର ।
Solution:
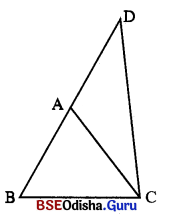
(i) △DBC ଅଙ୍କନ କର ଯାହାର BC = 7 ସେ.ମି., m∠DBC = 60° ଓ BD = 11.2 ସେ.ମି. ।
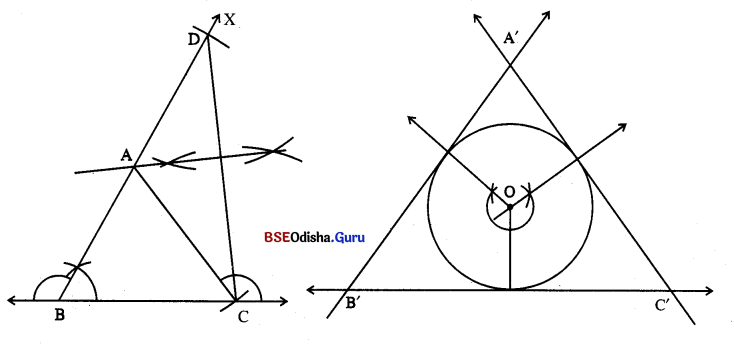
(ii) 1.5 ସେ.ମି. ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ବୃତ୍ତ ଅଙ୍କନ କରି Q. No. 2 ର ଅଙ୍କନ ପରି ବୃତ୍ତରେ △A’B’C’ ପରିଲିଖନ କର, ଯେପରି ABC ~ △A’B’C’ ହେବ ।
Question 7.
△ABC ଅଙ୍କନ କର ଯାହାର m∠A = 75°, AC = 9 ସେ.ମି., AB = 6 ସେ.ମି. । ତ୍ରିଭୁଜଟି ଅଙ୍କନ କରି ଏହାର ଏକ ସଦୃଶକୋଣୀ ତ୍ରିଭୁଜ 2 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତରେ ଅନ୍ତର୍ଲିଖନ କର ।
Solution:
(i) AC ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 9 ସେ.ମି. ।
(ii) ∠XAC ଅଙ୍କନ କର ଯେପରି M∠XAC = 75° |
(iii) A ବିନ୍ଦୁକୁ କେନ୍ଦ୍ରକରି 6 ସେ.ମି. ପରିମିତ ଏକ ଚାପ ଅଙ୍କନ କର ଯେପରି ଚାପଟି \( \overrightarrow{\mathrm{AX}}\) କୁ B ବିନ୍ଦୁରେ ଛେଦ କରିବ । \(\overline{\mathrm{BC}})\) ଅଙ୍କନ କର ।
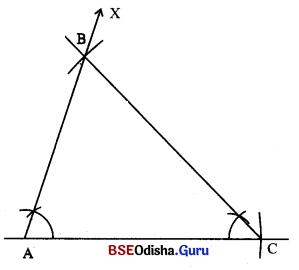
(iv) 2 ସେ.ମି. ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ବୃତ୍ତ ଅଙ୍କନ କରି Q.1 ର ଅଙ୍କନ ପରି ଏହାର ସଦୃଶ କୋଣୀ ତ୍ରିଭୁଜ A’B’C’ ଅଙ୍କନ କର ।