Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 11 ପରିମିତି Ex 11.1 Textbook Exercise Questions and Answers.
BSE Odisha Class 6 Maths Solutions Chapter 11 ପରିମିତି Ex 11.1
Question 1.
ତୁମ ଶ୍ରେଣୀରେ ପଡ଼ିଥିବା ଟେବୁଲର ଉପରି ଭାଗର ଚାରୋଟି ଯାକ ଧାରର ଦୈର୍ଘ୍ୟ ମାପ ଓ ତୁମେ ପାଇଥବା ମାପଗୁଡ଼ିକୁ ତଳେ ଦିଆଯାଇଥିବା ଭଳି ଲେଖ । (ପ୍ରଶ୍ନ ସହ ଉତ୍ତର)

ପ୍ରଥମ ଧାରର ଦୈର୍ଘ୍ୟ = _______ ସେ.ମି.,
ଦ୍ଵିତୀୟ ଧାରର ଦୈର୍ଘ୍ୟ = _______ ସେ.ମି.
ତୃତୀୟ ଧାରର ଦୈର୍ଘ୍ୟ = _______ ସେ.ମି.,
ଚତୁର୍ଥ ଧାରର ଦୈର୍ଘ୍ୟ = _______ ସେ.ମି.
ଏହାର ଚାରୋଟି ଧାରର ସମଷ୍ଟି = _______ ସେ.ମି. + _______ ସେ.ମି. + _______ ସେ.ମି. + _______ ସେ.ମି.
ଟେବୁଲ ଉପରିଭାଗର ପରିସାମା କେତେ ?
ସମାଧାନ:
ପ୍ରଥମ ଧାରର ଦୈର୍ଘ୍ୟ = 100 ସେ.ମି., ଦ୍ଵିତୀୟ ଧାରର ଦୈର୍ଘ୍ୟ = 60 ସେ.ମି.
ତୃତୀୟ ଧାରର ଦୈର୍ଘ୍ୟ = 100 ସେ.ମି., ଚତୁର୍ଥ ଧାରର ଦୈର୍ଘ୍ୟ = 60 ସେ.ମି.
ଏହାର ଚାରୋଟି ଧାରର ସମଷ୍ଟି = 100 ସେ.ମି. + 60 ସେ.ମି. + 100 ସେ.ମି. + 60 ସେ.ମି.
ଟେବୁଲ ଉପରି ଭାଗର ପରିସୀମା = 320 ସେ.ମି.
![]()
Question 2.
ତଳେ ଦିଆଯାଇଥିବା ଚିତ୍ର ମାନଙ୍କର ପରିସୀମା ନିର୍ଣ୍ଣୟ କର।
(କ)
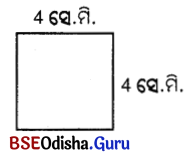
ସମାଧାନ:
ପରିସାମା = 4 × ଦୈର୍ଘ୍ୟ =4 × 4= 16 ସେ.ମି.
(ଖ)

ସମାଧାନ:
ପରିସୀମା = 2 (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ) = 2 (3 + 1) ସେ.ମି. = 8 ସେ.ମି.
(ଗ)
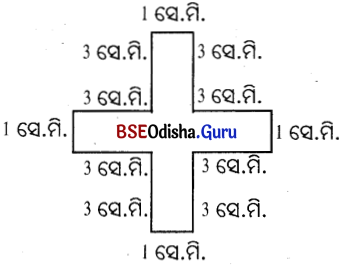
ସମାଧାନ:
ପରିସୀମା = 3 + 3 + 1 + 3 + 3 + 1 + 3 + 3 + 1 + 3 + 3 + 1 = 28 ସେ.ମି.
(ଘ)
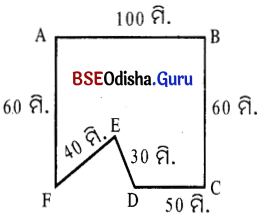
ସମାଧାନ:
ପରିସୀମା = AB + BC + CD + DE + EF + AF
= (100 + 60 + 50 + 30 + 40 + 60) ସେ.ମି. = 340 ସେ.ମି.
Question 3.
ଗୋଟିଏ ଆୟତାକୃତି ବିଶିଷ୍ଟ ପାର୍କର ଦୈର୍ଘ୍ୟ 50 ମିଟର ଓ ପ୍ରସ୍ଥ 35 ମିଟର । ଜଣେ ଖେଳାଳୀ ଏହି ପାର୍କର ଚାରିପାଖରେ 10 ଥର ଦଉଡ଼ିଲେ ସେ ମୋଟ କେତେ ବାଟ ଦୌଡ଼ିବେ ?
ସମାଧାନ:
ଆୟତାକୃତି ପାର୍କର ଦୈର୍ଘ୍ୟ = 50 ମି. ଓ ପ୍ରସ୍ଥ = 35 ମି. ।
∴ ପାର୍କର ପରିସୀମା = 2 (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ) = 2(50 + 35) ମି. = 2 × 85 ମି. = 170 ମି.
ଜଣେ ଖେଳାଳି 1 ଥର ଦୌଡ଼ିଲେ 170 ମି. ବାଟ ଯିବ
10 ଥର ଦୌଡ଼ିଲେ (170 × 10) ମି. = 1700 ମି.
∴ ଖେଳାଳୀ ଜଣକ ପାର୍କର ଚାରିପାଖରେ 10 ଥର ଦଉଡ଼ିଲେ ମୋଟ 1700 ମିଟର ବାଟ ଦୌଡ଼ିବ ।
Question 4.
ଗୋଟିଏ ଚତୁର୍ଭୁଜାକୃତି ବିଶିଷ୍ଟ ଜମିର ଚାରୋଟି ଯାକ ପାଖର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 15 ମିଟର, 12 ମିଟର, 17 ମିଟର ଓ 11 ମିଟର । ଏହାର ଚାରିପଟେ ବାଡ଼ ବୁଜିବାପାଇଁ ମିଟରପିଛା 6 ଟଙ୍କା ହିସାବରେ କେତେ ଖର୍ଚ୍ଚ ହେବ ?
ସମାଧାନ:
ଚତୁର୍ଭୁଜାକୃତି ଜମିର ପରିସୀମା = 15 ମି. + 12 ମି. + 17 ମି. + 11 ମି. = 55 ମି.
1 ମିଟର ବାଡ଼ବୁଜିବା ପାଇଁ ଖର୍ଚ୍ଚ ହୁଏ 6 ଟଙ୍କା ।
55 ମିଟର ବାଡ଼ବୁଜିବା ପାଇଁ ଖର୍ଚ୍ଚ ହେବ = (55 × 6) ଟଙ୍କା = 330 ଟଙ୍କା
∴ ଚତୁର୍ଭୁଜାକୃତି ବିଶିଷ୍ଟ ଜମିର ଚାରିପଟେ ବାଡ଼ବୁଜିବା ପାଇଁ 330 ଟଙ୍କା ଖର୍ଚ୍ଚ ହେବ ।
![]()
Question 5.
3 ମିଟର ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଗୋଟିଏ ଆୟତାକୃତି ବିଶିଷ୍ଟ ଟେବୁଲର ଉପରିଭାଗର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ଯଥାକ୍ରମେ 3 ମି. ଓ 1 ମି. 50 ସେ.ମି. । ଏହାର ଚାରି ଧାରରେ ସରୁ ରଙ୍ଗୀନ ଝାଲେରି ଲଗାଯିବ । କେତେ ମିଟର ଦୈର୍ଘ୍ୟର ରଙ୍ଗୀନ ଝାଲେରି ଆବଶ୍ୟକ ?
ସମାଧାନ:
ଟେବୁଲର ଦୈର୍ଘ୍ୟ = 3 ମି. ଓ ପ୍ରସ୍ଥ = 1 ମି. 50 ସେ.ମି.
ଟେବୁଲର ଚାରିଧାରର ପରିସୀମା = 2 (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ) = 2 (3 ମି. + 1 ମି. 50 ସେ.ମି.)
= 2 × 4 ମି. 50 ସେ.ମି. = 9 ମିଟର
∴ 9 ମିଟର ରଙ୍ଗୀନ ଝାଲେରି ଆବଶ୍ୟକ ।
Question 6.
ଗୋଟିଏ ବର୍ଗାକୃତି ବିଶିଷ୍ଟ ଟେବୁଲର ପରିସୀମା 3 ମି. 20 ସେ.ମି. । ଏହାର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ?
ସମାଧାନ:
ବର୍ଗାକୃତି ବିଶିଷ୍ଟ ଟେବୁଲର ସମସ୍ତ ବାହୁର ଦୈର୍ଘ୍ୟ ସମାନ ।
ବର୍ଗାକୃତି ବିଶିଷ୍ଟ ଟେବୁଲର ପରିସୀମା = 3 ମି. 20 ସେ.ମି. = 320 ସେ.ମି.
∴ ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ = ପରିସୀମା ÷ 4 = 320 ସେ.ମି. ÷ 4 = 80 ସେ.ମି.
Question 7.
ନିମ୍ନୋକ୍ତ କେଉଁ କେଉଁ କ୍ଷେତ୍ରରେ ପରିସୀମା ବାହାର କରିବା ଆବଶ୍ୟକ ପଡ଼ିବ ?

(କ) ଗୋଟିଏ ଋଷ ଜମିର ଋଷ କରାଯାଉଥିବା ସ୍ଥାନର ପରିମାଣ ନିର୍ଣ୍ଣୟ କରିବା।
ସମାଧାନ:
ପରିସୀମା ବାହାର କରିବା ଆବଶ୍ୟକ ପଡ଼ିବ ନାହିଁ ।
(ଖ) ଗୋଟିଏ ଖେଳପଡ଼ିଆର ଚାରିପଟେ ସାଇକେଲରେ ବୁଲିଆସିବା ।
ସମାଧାନ:
ପରିସୀମା ବାହାର କରିବା ଆବଶ୍ୟକ ପଡ଼ିବ ।
(ଗ) ଗୋଟିଏ କୋଠରିର ଚଟାଣରେ ମାର୍ବଲ ବିଛାଇବା।
ସମାଧାନ:
ପରିସୀମା ବାହାର କରିବା ଆବଶ୍ୟକ ପଡ଼ିବ ନାହିଁ ।
(ଘ) ଗୋଟିଏ ଫଟୋକୁ ବନ୍ଧାଇବା ପାଇଁ ଆବଶ୍ୟକ ପଡୁଥିବା କାଠର ଦୈର୍ଘ୍ୟ ଜାଣିବା।
ସମାଧାନ:
ପରିସୀମା ବାହାର କରିବା ଆବଶ୍ୟକ ପଡ଼ିବ ।
![]()
Question 8.
ଯଦି 30 ମିଟର ଦୀର୍ଘ ସରୁ ଲୁହା ତାର ଖଣ୍ଡେ ଆଣି ତାକୁ ଆବଶ୍ୟକମତେ ବଙ୍କାଇ ନିମ୍ନଲିଖୂତ ଆକୃତି କରାଯାଏ । ତେବେ ସେହି ଆକୃତିର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ହେବ ?
(କ) ବର୍ଗକ୍ଷେତ୍ର
ସମାଧାନ:
ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = ପରିସୀମା ÷ 4 = 30 ମି. ÷ 4 = 7 ମି. 50 ସେ.ମି.
(ଖ) ସୁଷମ ଷଡ଼ଭୁଜ
ସମାଧାନ:
ସୁଷମ ଷଡ଼ଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ = ପରିସୀମା ÷ 6 = 30 ମି. ÷ 6 = 5 ମି.
(ଗ) ସମବାହୁ ତ୍ରିଭୁଜ

ସମାଧାନ:
ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ = ପରିସୀମା ÷ 3 = 30 ମି. ÷ 3 = 10 ମି.
