BSE Odisha 6th Class Maths Solutions Chapter 3 ଜ୍ୟାମିତିରେ ମୌଳିକ ଧାରଣା Ex 3.2

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 3 ଜ୍ୟାମିତିରେ ମୌଳିକ ଧାରଣା Ex 3.2 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 3 ଜ୍ୟାମିତିରେ ମୌଳିକ ଧାରଣା Ex 3.2

Question 1. 
ଖାତାରେ ତିନୋଟି ବିନ୍ଦୁ ଚିହ୍ନିତ କରି ସେଗୁଡ଼ିକର ନାମ ଦିଅ ।
ସମାଧାନ:
A•  B•  •C

Question 2. 
ଦୁଇଟି ସରଳରେଖା ଅଙ୍କନ କରି ସେମାନଙ୍କର ନାମ ଦିଅ।
ସମାଧାନ:

\(\stackrel{\leftrightarrow}{\mathrm{AB}}\) ଓ \(\stackrel{\leftrightarrow}{\mathrm{CD}}\) ଦୁଇଟି ସରଳରେଖା।

Question 3. 
ତୁମ ପାଖଆଖରେ ଦେଖୁଥୁବା ତିନୋଟି ସରଳରେଖା, ତିନୋଟି ବକ୍ରତଳ ଓ ତିନୋଟି ସମତଳର ଉଦାହରଣ ଦିଅ ।
ସମାଧାନ:
ସରଳରେଖା – ସ୍କେଲର ଧାର, ଟେବୁଲର ଧାର, ବହିପୃଷ୍ଠାର ଧାର
ବକ୍ରତଳ – କାଚଗୋଲିର ପୃଷ୍ଠ, ପେଣ୍ଡୁର ପୃଷ୍ଠ, ରୁଲବାଡ଼ିର ପୃଷ୍ଠ ।
ସମତଳ – କାଗଜ ପୃଷ୍ଠ, ଟେବୁଲର ପୃଷ୍ଠ, ଛାତ

Question 4.
ନିମ୍ନ ଚିତ୍ରରେ ଥ‌ିବା ଗାରମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁଗୁଡ଼ିକ ସରଳରେଖା ଓ କେଉଁଗୁଡ଼ିକ ବକ୍ରରେଖା ଚିହ୍ନାଅ ।

ଲକ୍ଷ୍ୟ କର : ଚିତ୍ର ‘ଙ’ ରେ ଥ‌ିବା ରେଖାଟି ବହିର ପୃଷ୍ଠାକୁ ଦୁଇଟି ଭାଗରେ ପରିଣତ କରିଛି ଓ ଭାଗ ଦୁଇଟିକୁ ‘ପ’ ଓ ‘ଫ’ ଦ୍ଵାରା ଚିହ୍ନିତ କରାଯାଇଛି । ପ୍ରତ୍ୟେକ ଭାଗକୁ ରେଖାର ଗୋଟିଏ ପାର୍ଶ୍ବ ବୋଲି କୁହାଯାଏ।
ସମାଧାନ:
ଦତ୍ତ ଚିତ୍ର ମଧ୍ୟରୁ କ ଓ ଘ – ବକ୍ରରେଖା ଖ, ଗ ଓ ଙ – ସରଳରେଖା

Question 5.
ତୁମ ଖାତାରେ ଗୋଟିଏ ବିନ୍ଦୁ ଚିହ୍ନିତ କର ଓ ତା’ ମଧ୍ୟଦେଇ ସାତଟି ସରଳରେଖା ଅଙ୍କନ କର । ସେହି ବିନ୍ଦୁ ମଧ୍ୟ ଦେଇ ଆଉ କେତୋଟି ସରଳରେଖା ଅଙ୍କନ କରିପାରିବ ?
ସମାଧାନ:

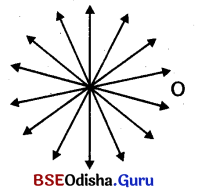
(i) ଖାତା ଉପରେ ଠ ବିନ୍ଦୁଦେଇ ସାତଟି ସରଳରେଖା ଅଙ୍କନ କର ।
(ii) ସେହି ବିନ୍ଦୁମଧ୍ୟଦେଇ ଅସଂଖ୍ୟ ସରଳରେଖା ଅଙ୍କନ କରାଯାଇପାରିବ ।

Question 6.
ତୁମ ଖାତାରେ A ଓ B ନାମକ ଦୁଇଟି ବିନ୍ଦୁ ନିଅ ଓ ଉଭୟ ବିନ୍ଦୁକୁ ଧାରଣ କରୁଥିବା ସରଳରେଖା ଅଙ୍କନ କର। ଏପରି କେତୋଟି ସରଳରେଖା ଅଙ୍କନ କରିପାରିବ?
ସମାଧାନ:
A ଓ B ଦୁଇଟି ବିନ୍ଦୁ ନିଆଗଲା । A ଓ B ବିନ୍ଦୁରେ \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) ଅଙ୍କନ କରାଗଲା । ଏହିପରି ଗୋଟିଏ ସରଳରେଖା ଅଙ୍କନ ହୋଇପାରିବ ।
A ଓ B ମଧ୍ୟଦେଇ \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) ଭିନ୍ନ ଅନ୍ୟ ସରଳରେଖା ଅଙ୍କନ ସମ୍ଭବ ନୁହେଁ ।

Question 7.
(କ) ସାଧାରଣ ବିନ୍ଦୁ ଥବା ଦୁଇଟି ସରଳ ରେଖା ଅଙ୍କନ କର ସେହି ଦୁଇ ସରଳରେଖାକୁ ନାମକରଣ କର। ସାଧାରଣ ବିନ୍ଦୁର ନାମ P ଦିଅ ।
ସମାଧାନ:

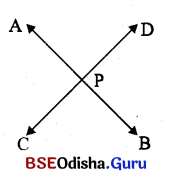
\(\stackrel{\leftrightarrow}{\mathrm{AB}}\) ଓ \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) ଦୁଇଟି ପରସ୍ପର ଛେଦୀ ସରଳରେଖା । ସରଳରେଖାଦ୍ବୟର ସାଧାରଣ ବିନ୍ଦୁ P ।

(ଖ) ତୁମ ଖାତା ଉପରେ ଯେ କୌଣସି ସାତଟି ବିନ୍ଦୁ ନିଅ। ସେଗୁଡ଼ିକର ନାମ ଦିଅ। ସେଗୁଡିକ ଏକରେଖୀ ହେଉଛନ୍ତି କି? କିପରି ଜାଣିଲ?
ସମାଧାନ:

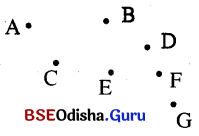
ଏହି ବିନ୍ଦୁମାନ ଏକରେଖା ଉପରିସ୍ଥ ନୁହଁନ୍ତି । ଏମାନେ ଅଣରେଖୀୟ ବିନ୍ଦୁ ।

Question 8.
ଗୋଟିଏ ସମତଳରେ ଥିବା ତିନୋଟି ସରଳରେଖା ପରସ୍ପରକୁ ଅତି କମ୍‌ରେ କେତୋଟି ବିନ୍ଦୁରେ ଛେଦ କରିବେ? ଅତି ବେଶିରେ କେତୋଟି ବିନ୍ଦୁରେ ଛେଦ କରିବେ?
ସମାଧାନ:
(i) ଗୋଟିଏ ସମତଳରେ ଥ‌ିବା ତିନୋଟି ସରଳରେଖା ପରସ୍ପରକୁ ଅତିକମ୍‌ରେ ଗୋଟିଏ ବିନ୍ଦୁରେ ଛେଦ କରିବେ । (ଚିତ୍ର ‘କ’ ଓ ଚିତ୍ର ‘ଖ’)

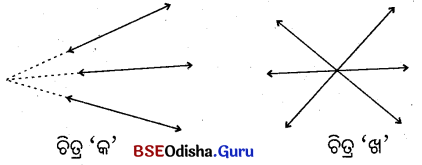
(ii)

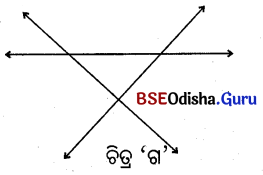
ଗୋଟିଏ ସମତଳରେ ଥ‌ିବା ତିନୋଟି ସରଳରେଖା ପରସ୍ପରକୁ ଅତିବେଶିରେ ତିନୋଟି ବିନ୍ଦୁରେ ଛେଦ କରିବେ । (ଚିତ୍ର ‘ଗ’)

Question 9.
ସ୍କେଲ୍ ବ୍ୟବହାର କରି ଦୁଇଟି ସରଳରେଖା ଅଙ୍କନ କର, ଯେପରି ସରଳରେଖା ଦ୍ଵୟ ସମାନ୍ତର ହେବେ ।
ସମାଧାନ:

\(\overleftrightarrow{\mathrm{AB}}\) ଓ \(\overleftrightarrow{\mathrm{CD}}\) ପରସ୍ପର ସମାନ୍ତର ।

Question 10. 
ନିମ୍ନସ୍ଥ ବାକ୍ୟମାନଙ୍କ ମଧ୍ୟରୁ ଠିକ୍ ବାକ୍ୟଗୁଡ଼ିକୁ ବାଛି ଲେଖ ।
(କ) ‘ରେଖା’ କହିଲେ ଆମେ କେବଳ ‘ସରଳରେଖା’କୁ ବୁଝୁ ।
(ଖ) ଗୋଟିଏ ବିନ୍ଦୁ ମଧ୍ୟ ଦେଇ ଅସଂଖ୍ୟ ସରଳରେଖା ଅଙ୍କନ କରାଯାଇପାରିବ ।
(ଗ) ଏକ ସମତଳରେ ଅବସ୍ଥିତ ଦୁଇଟି ବିନ୍ଦୁ ମଧ୍ୟଦେଇ ଅସଂଖ୍ୟ ସରଳରେଖା ଅଙ୍କନ କରାଯାଇପାରିବ । 
(ଘ) ଏକ ସମତଳ ଉପରିସ୍ଥ ଗୋଟିଏ ବିନ୍ଦୁଦେଇ ମାତ୍ର ଗୋଟିଏ ସରଳରେଖା ଅଙ୍କନ କରାଯାଇପାରିବ । 
(ଙ) ଏକ ସମତଳରେ ଥ‌ିବା ଦୁଇଟି ବିନ୍ଦୁକୁ ଧାରଣ କରୁଥିବା ଗୋଟିଏ ମାତ୍ର ସରଳରେଖା ଅଙ୍କନ ସମ୍ଭବ । 
(ଚ) ଏକ ସମତଳ ଉପରିସ୍ଥ ଦୁଇଟି ଅସମାନ୍ତର ସରଳରେଖା ପରସ୍ପରକୁ ଗୋଟିଏ ମାତ୍ର ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । 
(ଛ) ଦୁଇଟି ସମାନ୍ତର ସରଳରେଖାର କୌଣସି ଛେଦବିନ୍ଦୁ ନାହିଁ ।
ସମାଧାନ:
(କ), (ଖ), (ଙ), (ଚ), (ଛ) ବାକ୍ୟଗୁଡ଼ିକ ଠିକ୍ ।