Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 3 ଜ୍ୟାମିତିରେ ମୌଳିକ ଧାରଣା Ex 3.6 Textbook Exercise Questions and Answers.
BSE Odisha Class 6 Maths Solutions Chapter 3 ଜ୍ୟାମିତିରେ ମୌଳିକ ଧାରଣା Ex 3.6
Question 1.
(କ) ନିମ୍ନଲିଖିତ ମାପବିଶିଷ୍ଟ କୋଣମାନଙ୍କର ଅନୁପୂରକ କୋଣର ମାପ ନିର୍ଣ୍ଣୟ କର ।
6°, 15°, 29°, 30°, 45°, 75°
ସମାଧାନ:
(i) 6° ର ଅନୁପୂରକ କୋଣର ମାପ = (90° – 6°) = 84°
(ii) 15° ର ଅନୁପୂରକ କୋଣର ମାପ = (90° – 15°) = 75°
(iii) 29° ର ଅନୁପୂରକ କୋଣର ମାପ = (90° – 29°) = 61°
(iv) 30° ର ଅନୁପୂରକ କୋଣର ମାପ = (90° – 30°) = 60°
(v) 45° ର ଅନୁପୂରକ କୋଣର ମାପ = (90° – 45°) = 45°
(vi) 75° ର ଅନୁପୂରକ କୋଣର ମାପ = (90° – 75°) = 15°
(ଖ) ନିମ୍ନଲିଖତ ମାପବିଶିଷ୍ଟ କୋଣମାନଙ୍କର ପରିପୂରକ କୋଣର ମାପ ନିର୍ଣ୍ଣୟ କର ।
27°, 52°, 70°, 110°, 145°, 150°
ସମାଧାନ:
(i) 27° ର ପରିପୂରକ କୋଣର ମାପ = (180° – 27°) = 153°
(ii) 52° ର ପରିପୂରକ କୋଣର ମାପ = (180° – 52°) = 128°
(iii) 70° ର ପରିପୂରକ କୋଣର ମାପ = (180° – 70°) = 110°
(iv) 110° ର ପରିପୂରକ କୋଣର ମାପ = (180° – 110°) = 70°
(v) 145° ର ପରିପୂରକ କୋଣର ମାପ = (180° – 145°) = 35°
(vi) 150° ର ପରିପୂରକ କୋଣର ମାପ = (180° – 150°) = 30°
Question 2.
(କ) 45° 45′ ମାପ ବିଶିଷ୍ଟ କୋଣର ଅନୁପୂରକ ଓ ପରିପୂରକ କୋଣର ମାପ ନିର୍ଣ୍ଣୟ କର । (1° = 60′)।
ସମାଧାନ:
45° 45′ ମାପ ବିଶିଷ୍ଟ କୋଣର ଅନୁପୂରକ କୋଣର ମାପ = (90° – 45° 45′) = 44° 15′
45° 45′ ମାପ ବିଶିଷ୍ଟ କୋଣର ଅନୁପୂରକ କୋଣର ମାପ = (180° – 45° 45′) = 134° 15′
(ଖ) 48° ମାପବିଶିଷ୍ଟ କୋଣର ଅନୁପୂରକ କୋଣର ପରିପୂରକ କୋଣର ପରିମାଣ କେତେ?
ସମାଧାନ:
48° ମାପବିଶିଷ୍ଟ କୋଣର ଅନୁପୂରକ କୋଣର ପରିମାଣ = (90° – 48°) = 42°
42° ମାପବିଶିଷ୍ଟ କୋଣର ପରିପୂରକ କୋଣର ପରିମାଣ = (180° – 42°) = 138°
∴ 48° ମାପବିଶିଷ୍ଟ କୋଣର ଅନୁପୂରକ କୋଣର ପରିପୂରକ କୋଣର ପରିମାଣ 138° ।
![]()
Question 3.
ନିମ୍ନ ମାପବିଶିଷ୍ଟ ଯୋଡ଼ିମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁ ଯୋଡ଼ି ପରସ୍ପର ଅନୁପୂରକ ଓ କେଉଁ ଯୋଡ଼ି ପରସ୍ପର ପରିପୂରକ ଚିହ୍ନଟ କର ।
(କ) 68°, 22°
ସମାଧାନ:
68°, 22° → 68° + 22° = 90° (ଅନୁପୂରକ)
(ଖ) 163°, 17°
ସମାଧାନ:
163°, 17° → 163° + 17° = 180° (ପରିପୂରକ)
(ଗ) 73°, 17°
ସମାଧାନ:
73°, 17° → 73° + 17° = 90° (ଅନୁପୂରକ)
(ଘ) 80°, 10°
ସମାଧାନ:
80°, 10° → 80° + 10° = 90° (ଅନୁପୂରକ)
(ଙ) 42°, 138°
ସମାଧାନ:
42°, 138° → 42° + 138° = 180° (ପରିପୂରକ)
(ଚ) 90°, 90°
ସମାଧାନ:
90°, 90° → 90° + 90° = 180° (ପରିପୂରକ)
Question 4.
ଚିତ୍ର ଅଙ୍କନକରି ଅନୁପୂରକ କୋଣ ଓ ପରିପୂରକ କୋଣ ଯୋଡ଼ିମାନଙ୍କର ଉଦାହରଣ ଦିଅ ।
ସମାଧାନ:
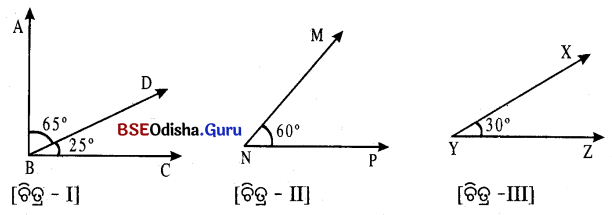
ଚିତ୍ର-I ରେ ∠ABD ଓ ∠CBD ଯୋଡ଼ି ପରସ୍ପର ଅନୁପୂରକ ।
ଚିତ୍ର – II ଓ ଚିତ୍ର – III ର ∠MNP ଓ ∠XYZ ପରସ୍ପର ଅନୁପୂରକ ।
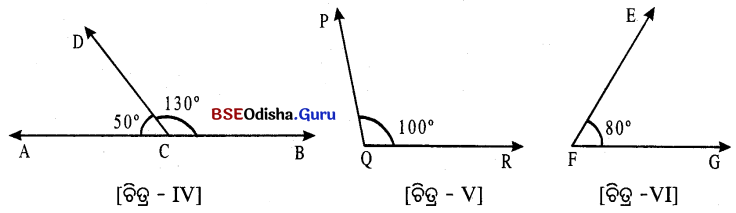
ଚିତ୍ର-IV ରେ ∠ACD ଓ ∠BCD ଯୋଡ଼ି ପରସ୍ପର ପରିପୂରକ ।
ଚିତ୍ର – V ଓ ଚିତ୍ର – VI ର ∠POR ଓ ∠EFG ଯୋଡ଼ି ପରସ୍ପର ପରିପୂରକ ।
Question 5.
ତୁମ ଆଖପାଖରେ ଥିବା ବସ୍ତୁମାନଙ୍କ ମଧ୍ୟରୁ ପରସ୍ପର ପ୍ରତି ସମକୋଣରେ ରହୁଥିବା ବସ୍ତୁମାନଙ୍କର ତିନୋଟି ଉଦାହରଣ ଦିଅ।
ସମାଧାନ:
ଆମ ଆଖପାଖରେ ଥିବା ବସ୍ତୁମାନଙ୍କ ମଧ୍ୟରୁ ପରସ୍ପର ପ୍ରତି ସମକୋଣରେ ରହୁଥିବା ବସ୍ତୁଗୁଡ଼ିକ ହେଲା –
(i) ଫଟୋଫ୍ରେମ୍ (ii) ଦୁଆର ବନ୍ଧ (iii) ଟେବୁଲ୍ ଗୋଡ଼
![]()
Question 6.
ଗୋଟିଏ ଟ୍ରାଫିକ୍ ପୋଲିସ୍ ପୂର୍ବକୁ ମୁହଁ କରି ଠିଆ ହୋଇଛି। ଯଦି ସେ ତା’ର ବାମକୁ କ୍ରମାନ୍ୱୟରେ

ସମାଧାନ:
(କ) ଏକ ସମକୋଣ
ସମାଧାନ:
ପୂର୍ବରୁ ଏକ ସମକୋଣ ବାମକୁ ଘୂରିଲେ ମୁହଁ ଉତ୍ତର ଦିଗକୁ ରହିବ ।
(ଖ) ଦୁଇ ସମକୋଣ
ସମାଧାନ:
ପୂର୍ବରୁ ଦୁଇ ସମକୋଣ ବାମକୁ ଘୂରିଲେ ମୁହଁ ପଶ୍ଚିମ ଦିଗକୁ ରହିବ ।
(ଗ) ତିନି ସମକୋଣ
ସମାଧାନ:
ପୂର୍ବରୁ ତିନି ସମକୋଣ ବାମକୁ ଘୂରିଲେ ମୁହଁ ଦକ୍ଷିଣ ଦିଗକୁ ରହିବ ।
(ଘ) ଚାରି ସମକୋଣ ଘୂରେ, ତେବେ ପ୍ରତି ଥର ଘୂରିବା ପରେ ତା’ର ମୁହଁ କେଉଁ ଦିଗକୁ ରହିବ?
ସମାଧାନ:
ପୂର୍ବରୁ ଚାରି ସମକୋଣ ବାମକୁ ଘୂରିଲେ ମୁହଁ ପୁନଶ୍ଚ ପୂର୍ବ ଦିଗକୁ ରହିବ ।
Question 7.
କି ପ୍ରକାର କୋଣ ସୃଷ୍ଟି ହେବ?
ସମାଧାନ:
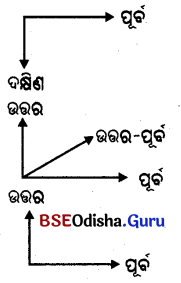
(କ) ଗୋଟିଏ ବିନ୍ଦୁରୁ ପୂର୍ବ ଓ ଦକ୍ଷିଣକୁ ଦୁଇଟି ରଶ୍ମି ଅଙ୍କନ କଲେ।
ସମାଧାନ:
ଗୋଟିଏ ବିନ୍ଦୁରୁ ପୂର୍ବ ଓ ଦକ୍ଷିଣକୁ ଦୁଇଟି ରଶ୍ମି ଅଙ୍କନ କଲେ, ସମକୋଣ (90°) ସୃଷ୍ଟି ହେବ ।
(ଖ) ଗୋଟିଏ ବିନ୍ଦୁରୁ ଉତ୍ତର ଓ ଉତ୍ତର ପୂର୍ବକୁ ଦୁଇଟି ରଶ୍ମି ଅଙ୍କନ କଲେ ।
ସମାଧାନ:
ଗୋଟିଏ ବିନ୍ଦୁରୁ ଉତ୍ତର ଓ ଉତ୍ତର ପୂର୍ବକୁ ଦୁଇଟି ରଶ୍ମି ଅଙ୍କନ କଲେ ସୂକ୍ଷ୍ମକୋଣ (45°) ସୃଷ୍ଟି ହେବ ।
(ଗ) ଗୋଟିଏ ବିନ୍ଦୁରୁ ପୂର୍ବ ଓ ଉତ୍ତରକୁ ଦୁଇଟି ରଶ୍ମି ଅଙ୍କନ କଲେ।
ସମାଧାନ:
ଗୋଟିଏ ବିନ୍ଦୁରୁ ପୂର୍ବ ଓ ଉତ୍ତରକୁ ଦୁଇଟି ରଶ୍ମି ଅଙ୍କନ କଲେ ସମକୋଣ (90°) ସୃଷ୍ଟି ହେବ ।
Question 8.
(କ) ଯେଉଁ କୋଣର ପରିମାଣ ତା’ର ଅନୁପୂରକ କୋଣର ପରିମାଣର ଦୁଇଗୁଣ, ତା’ର ପରିମାଣ କେତେ?
ସମାଧାନ:
ମନେକର ଅନୁପୂରକ କୋଣର ପରିମାଣ l ଗୁଣ ଓ କୋଣଟିର ପରିମାଣ 2 ଗୁଣ ।
1 ଗୁଣ + 2 ଗୁଣ = 3 ଗୁଣ, 3 ଗୁଣ = 90°
1 ଗୁଣ = \(\frac{90^{\circ}}{3}\) = 30°, 2 ଗୁଣ = 30° × 2 = 60°
∴ କୋଣର ପରିମାଣ 60° ।
(ଖ) ଯେଉଁ କୋଣର ପରିମାଣ ତା’ର ପରିପୂରକ କୋଣର ପରିମାଣର ଦୁଇଗୁଣ, ତା’ର ପରିମାଣ କେତେ?
ସମାଧାନ:
ମନେକର ପରିପୂରକ କୋଣର ପରିମାଣ 1 ଗୁଣ ଓ କୋଣଟିର ପରିମାଣ 3 ଗୁଣ ।
1 ଗୁଣ + 2 ଗୁଣ = 3 ଗୁଣ, 3 ଗୁଣ = 180°, 1 ଗୁଣ = \(\frac{180^{\circ}}{3}\) = 60°
2 ଗୁଣ = 60° × 2 = 120°
∴ କୋଣଟିର ପରିମାଣ 120°
