Odisha State Board BSE Odisha 7th Class Science Solutions Chapter 11 ଗତି ଓ ସମୟ Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Science Solutions Chapter 11 ଗତି ଓ ସମୟ
Question 1.
ତଳେ ଦିଆଯାଇଥିବା ପ୍ରତ୍ୟେକ ଗତି କେଉଁ ପ୍ରକାର ଗତି (ସରଳରେଖକ, ବୃତ୍ତାକାର, ଦୋଳନ, ଆବୃତ୍ତି) ବା ଏକାଧ୍ଵ ଗତିର ସମ୍ମିଶ୍ରଣ ଲେଖ ।
(କ) ତୁମେ ସିଧା ରାସ୍ତାରେ ଦୌଡ଼ିଲା ବେଳେ ତୁମ ହାତର ଗତି ।
(ଖ) ଗୋଟିଏ ବିଦ୍ୟୁତ୍ ଘଣ୍ଟିରେ ହାତୁଡ଼ିର ଗତି (ଘଣ୍ଟି ବାଜିଲାବେଳେ) ।
(ଗ) ବର୍ଷା ହେଉଥିବା ବେଳେ ସିଧା ରାସ୍ତାରେ ଯାଉଥିବା ଗୋଟିଏ କାର୍ର ସାମନା କାଚ ୱାଇପର୍ର ଗତି
(ଘ) ପବନ ସାମ୍ନାରେ ଥିବା କାଗଜ ତିଆରି ଚକ୍ରିର ଗତି ।
(ଙ) ଗୋଟିଏ ବିଦୁପତ୍ ତାଲିତ ଖେଲନା ଖାହ୍ ଦକାଲିଲା ବେଳେ ହେଲନାର ହାତର ଉଚି |
(ଚ) ଗୋଟିଏ ସିଧା ପୋଲ ଉପରେ ଯାଉଥିବା ଗୋଟିଏ ଟ୍ରେନ୍ର ଗତି ।
Solution:
(କ) ଦୋଳନ ଓ ସରଳରେଖ
(ଗ) ଦୋଳନ ଗତି
(ଙ) ଦୋଳନ ଗତି/ଆବୃତ୍ତି
(ଖ) ଦୋଳନ |ଆବୃତ୍ତି
(ଚ) ସରଳରେଖ୍ୟ ଗତି
![]()
Question 2.
ତୁମେ ଦେଖିବା ତଥା ସରଳରେଖ୍କ ଗତି କରୁଥିବା ଗୋଟିଏ ବସ୍ତୁର ନାମ ଲେଖ ।
Solution:
- ସଳଖ ଓ ସମତଳ ରାସ୍ତାରେ ଗଡ଼ିଯାଉଥିବା ପେଣ୍ଡୁର ଗତି, ସଳଖ ରାସ୍ତାରେ ଏକ ନିଦ୍ଦିଷ୍ଟ ଦିଗରେ ଗତି କରୁଥିବା ଯାନ ।
- ସଳଖ ରାସ୍ତାରେ ଏକ ନିଦିକୁ ବିଗରେ ଗତି କରୁଥିବା ଯାନ |
Question 3.
ଚିତ୍ର ୧୧.୧୧ ବ୍ୟବହାର କରି କାର୍ର ବେଗ ନିର୍ଣ୍ଣୟ କର ।
Solution:
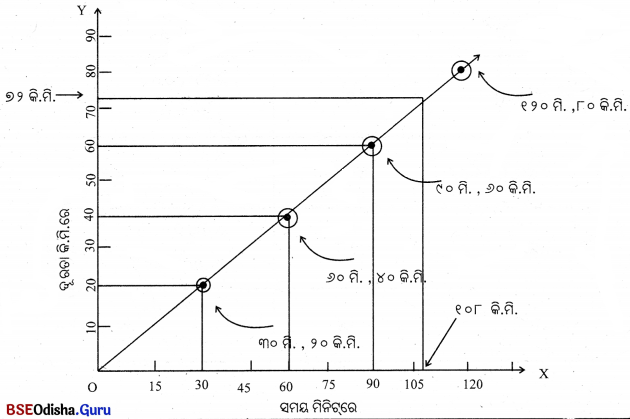
୩୦ ମିନିଟ୍ରେ କାର୍ର ଅତିକ୍ରାନ୍ତ ଦୂରତା ୨୦ କି.ମି. ।

![]()
Question 4.
ସମୟ ଅନୁସାରେ ଗୋଟିଏ କାର୍ ଗତି କରିଥିବା ଦୂରତାର ସାରଣୀ ତଳେ ଦିଆଯାଇଛି ।
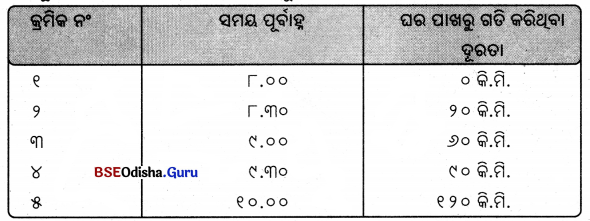
ତୁମେ ଆଗରୁ ଆଙ୍କିଥିବା ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ରେ ଏଇ ସାରଣୀ ବ୍ୟବହାର କରି ଅନ୍ୟ ଏକ ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ଅଙ୍କନ କର ।
(କ) ଦୁଇଟି ଗ୍ରାଫ୍ ମଧ୍ୟରେ କ’ଣ ପ୍ରଭେଦ ଲକ୍ଷ୍ୟ କରୁଛ ?
(ଖ) ପ୍ରତ୍ୟେକ ଗ୍ରାଫ୍ X-ଅକ୍ଷ ସହିତ ଆନତ କୋଣ କ’ଣ ସମାନ ?
(ଗ) ଏହି ଆନତ କୋଣ ସହିତ ବସ୍ତୁର ବେଗର କେଉଁ ସଂପର୍କ ଲକ୍ଷ୍ୟ କରୁଛ ଲେଖ ।
Solution:
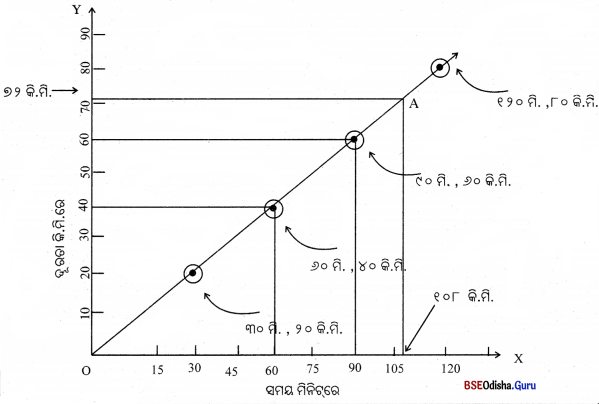
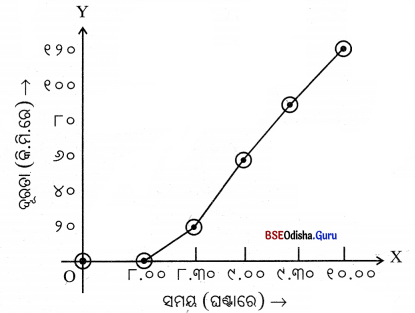
(i) ପ୍ରଥମ ଗ୍ରାଫ୍ଟି ଏକ ସରଳରେଖା, ଏବଂ ଏହା ମୂଳ ବିନ୍ଦୁ O ରୁ ବାହାରିଛି । ଏଥୁରୁ ବସ୍ତୁର ସମବେଗର ସୂଚନା ମିଳିଥାଏ ।
(ii) ଦ୍ବିତୀୟ ଗ୍ରାଫ୍ଟି ଏକ ସରଳରେଖା ନୁହେଁ ଏବଂ ଏହା ମୂଳ ବିନ୍ଦୁରୁ ନ ବାହାରି X- ଅକ୍ଷରୁ ବାହାରିଥାଏ । ଏଥୁରୁ ବସ୍ତୁର ଅସମ ବେଗର ସୂଚନା ମିଳିଥାଏ ।
(ଖ) ପ୍ରତ୍ୟେକ ଗ୍ରାଫ୍ X- ଅକ୍ଷ ସହିତ ଆନତ କୋଣ ସମାନ ନୁହେଁ ।
(ଗ) ଆନତ କୋଣ କମ୍ ହେଲେ ବେଗ କମ୍ ହୋଇଥାଏ । ଆନତ କୋଣ ଅଧିକ ହେଲେ ବେଗ ଅଧିକ ହୋଇଥାଏ ।
Question 5.
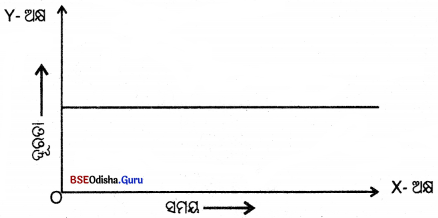
ଗୋଟିଏ ବସ୍ତୁର ସମୟ -ଦୂରତା ଗ୍ରାଫ୍ ତଳେ ଦିଆଗଲା । ବସ୍ତୁଟି କେଉଁ ପ୍ରକାର ଗତି କରୁଛି ଲେଖ ।
Solution:
ଏଠାରେ ବସ୍ତୁଟିର ଦୂରତା ସମୟ ଅନୁସାରେ ପରିବର୍ତ୍ତନ ହେଉନାହିଁ । ତେଣୁ ବସ୍ତୁଟି ସ୍ଥିର ରହିଥିବାର ସୂଚନା ମିଳୁଛି ।
Question 6.
ତୁମେ ସାଇକେଲ୍ ଚଳାଇ ଗଲାବେଳେ ତୁମର ବେଗ ୧୨ କି.ମି./ଘଣ୍ଟା । ଗୋଟିଏ ମହୁମାଛି ଉଡ଼ିଲାବେଳେ ତା’ର ବେଗ ୫ ମି./ସେ. । ତୁମର ଓ ମହୁମାଛିର ବେଗ ଭିତରେ କାହାର ବେଗ ଅଧୁକ ଅଟେ ?
Solution:

Question 7.
ଗୋଟିଏ କାର୍ ୧୫ ମିନିଟ୍ କାଳ ୪୦ କି.ମି. |ଘଣ୍ଟା ବେଗରେ ଗତି କଲା । ତା’ପରେ ୨୦ ମିନିଟ୍ କାଳ ୬୦ କି.ମି. | ଘଣ୍ଟା ବେଗରେ ଗତି କଲା । ଏଇ ଯାତ୍ରାରେ କାର୍ର ହାରାହାରି ବେଗ କେତେ ?
Solution:

![]()
Question 8.
ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ ଭୁଲ ଉକ୍ତିଗୁଡ଼ିକ ସଂଶୋଧନ କରି ତୁମ ଖାତାରେ ଲେଖ ।
(କ) ସମୟର ମୌଳିକ ଏକକ ଘଣ୍ଟା ଅଟେ ।
(ଖ) ଦୁଇଟି ସହର ମଧ୍ୟରେ ଦୂରତା କିଲୋମିଟରରେ ମପାଯାଏ ।
(ଗ) ପ୍ରତ୍ୟେକ ବସ୍ତୁ ଗତି କଲାବେଳେ ସାଧାରଣତଃ ଏକ ସମାନ ବେଗରେ ଗତି କରିଥାନ୍ତି ।
(ଘ) ଗୋଟିଏ ସରଳ ଦୋଳକର ଦୋଳନ ସମୟ ଧ୍ରୁବ ନୁହେ ।
(ଙ) ଟ୍ରେନ୍ର ବେଗ ମି./ ଘଣ୍ଟାରେ ପ୍ରକାଶ କରାଯାଏ ।
Solution:
(କ) ସମୟର ମୌଳିକ ଏକକ ସେକେଣ୍ଡ ଅଟେ ।
(ଖ) ଦୁଇଟି ସହର ମଧ୍ୟରେ ଦୂରତା କିଲୋମିଟରରେ ମପାଯାଏ ।
(ଗ) ପ୍ରତ୍ୟେକ ବସ୍ତୁ ଗତି କଲାବେଳେ ସାଧାରଣତଃ ଏକ ଅସମ ବେଗରେ ଗତି କରିଥାନ୍ତି ।
(ଘ) ଗୋଟିଏ ସରଳ ଦୋଳକର ଦୋଳନ ସମୟ ଧ୍ରୁବ ଅଟେ ।
(ଙ) ଟ୍ରେନର ବେଗ କି.ମି.|ଘ.ରେ ପ୍ରକାଶ କରାଯାଏ ।
Question 9.
ବେଗର ପୌଲିକ ଏକକ
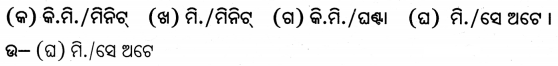
Question 10.
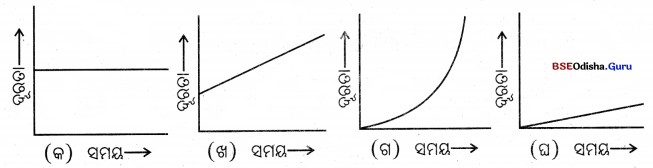
ତଳେ ଚାରୋଟି ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ଦିଆଯାଇଛି । ସେଥ୍ମଧ୍ୟରୁ କେଉଁଟି ଗୋଟିଏ କାର୍ର ଅସମ ଗତିର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ଅଟେ ?
Solution:
(ଗ) ଗ୍ରାଫ୍ଟି କାରର ଅସମ ଗତିର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ।
Question 11.
ଗୋଟିଏ ଗତିଶୀଳ କାରର ଓଡ଼ୋମିଟରର ମାପାଙ୍କ ପୂର୍ବାହ୍ନ ୦୮.୦୦ରେ ୬୩୨୧୯.୦ କି.ମି. ଓ ପୂର୍ବାହ୍ନ ୦୮.୩୫ରେ ୬୩୩୦୯.୦ କି.ମି. ଅଟେ । ଏଇ ସମୟ ଅନ୍ତରାଳରେ କାର୍ର ବେଗ କି.ମି. | ମିନିଟ୍ ତଥା କି.ମି. | ଘଣ୍ଟାରେ ପ୍ରକାଶ କର ।
Solution:
ଗତିଶୀଳ କାର୍ର ଓଡ଼ୋମିଟରର ମାପାଙ୍କ ପୂର୍ବାହ୍ନ ୮.୦୦ରେ ୬୩୨୧୯.୦ କି.ମି. ଥିଲା ଏବଂ ପୂର୍ବାହ୍ନ ୮.୩୫ରେ ୬୩୩୦୯.୦ କି.ମି. ହେଲା ।
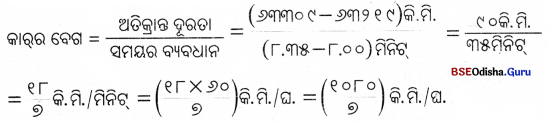
Question 12.
ମନେକର ଯେ ଚିତ୍ର ୧୧.୧ ଓ ୧୧.୨ରେ ଦର୍ଶାଯାଇଥିବା ଫଟୋ ଦୁଇଟି ୧୦ସେ. ଅନ୍ତରାଳରେ ନିଆଯାଇଛି । ଯଦି ଫଟୋ ଗୁଡ଼ିକରେ ୧୦୦ମି. ଦୂରତା ୧ ସେ.ମି. ରୂପରେ ଦର୍ଶାଯାଇଛି ତେବେ ନୀଳକାର୍ର ବେଗ ନିର୍ଣ୍ଣୟ କର ।

ବିପଯୁବସ୍ତୁ ସପୂଜାପ ପୂଚନା ଓ ବିଶେଷଣ :
→ ଗତି :
- ଦିଗ ଓ ଦୂରତା ସମୟ ଅନୁସାରେ ନ ବଦଳିଲେ ବସ୍ତୁଟି ସ୍ଥିର ଏବଂ ଏଥୁରୁ କୌଣସି ଗୋଟିଏ ବି ବଦଳିଲେ ତାହା ଗତିଶୀଳ ।
- ଗତି ସାଧାରଣତଃ ଚାରି ପ୍ରକାରର ଅଟେ ; ଯଥା – ସରଳରୈଖ୍ୟକ ଗତି, ବୃତ୍ତୀୟ ଗତି, ଆବର୍ତୀ ଗତି ଏବଂ ହୋଇନ ଗତି |
→ ସରଳରୈଖ୍ୟକ ଗତି :
ବସ୍ତୁଟି ଗୋଟିଏ ସରଳରେଖାରେ ଗତି କଲେ ତା’ର ଗତିକୁ ସରଳରେଖ୍ୟ ଗତି କୁହାଯାଏ ।
ଉଦାହରଣ ସ୍ଵରୂପ, ପେଣ୍ଡୁଟିଏ ଗଡ଼େଇଲେ ସେ ସରଳରେଖାରେ ଗତି କରିଥାଏ, ଆଲୋକ ଏକ ସରଳରେଖାରେ ଗତି କରିଥାଏ ।
→ ବୃତ୍ତୀୟ ଗତି :
ଯଦି କୌଣସି ବସ୍ତୁ ବୃତ୍ତାକାର ପଥରେ ଗତି କରୁଥାଏ, ତେବେ ତା’ର ଗତିକୁ ବୃତ୍ତୀୟ ଗତି କୁହାଯାଏ । ଉଦାହରଣ ସ୍ୱରୂପ – ଚକ୍ତିବାଣର ଗତି, ସାଇକେଲ୍ ଚକର ଗତି, ଚକ୍ରିଦୋଳିର ଗତି ଇତ୍ୟାଦି ।
→ ଆବର୍ତ୍ତୀ ଗତି :
ସୂର୍ଯ୍ୟ ଚାରିପାଖରେ ପୃଥିବୀର ଗତି, ନିଜର ଅକ୍ଷ ଚାରିପାଖରେ ବୁଲୁଥବା ପୃଥିବୀର ଗତି ଇତ୍ୟାଦି ଆବର୍ତୀ ଗଢିର ଉଦାହରଣ |
→ ଦୋଳନ ଗତି :
ତୁମେ ଦୋଳି ଖେଳୁଥିବାବେଳେ ଦୋଳିଟି ଏପଟ ସେପଟ ହୋଇ ଅର୍ଥାତ୍ ଥରେ ଆଗକୁ ଓ ପଛକୁ ଗତି କରିଥାଏ । ସେହିପରି ଭାବରେ ଘଣ୍ଟାରେ ଥିବା ଦୋଳକ ଓ ପେଣ୍ଡୁଲମ୍ ଏପଟ ଓ ସେପଟ ହୋଇ ଗତି କରିଥାଏ । ଏହି ପ୍ରକାର ଗତିକୁ ଦୋଳନ ଗତି କୁହାଯାଏ ।
![]()
→ ଧୀର ଅଥବା ଦୃତ ଗତି :
(i) କେତେକ ବସ୍ତୁ ଅନ୍ୟ କିଛି ବସ୍ତୁ ତୁଳନାରେ ଦ୍ରୁତତର ଗତିରେ ଗତି କରିଥାନ୍ତି ।
(ii) ଉଦାହରଣ ସ୍ୱରୂପ ମଟରଗାଡ଼ି, ଶଗଡ଼ଠାରୁ ଦ୍ରୁତତର ଗତିରେ ଗତି କରିଥାଏ । ଏଠାରେ ମଟରଗାଡ଼ି ଦ୍ରୁତ ଗତିରେ ଗତି କରିଥାଏ ଏବଂ ଶଗଡ଼ଗାଡ଼ି ଧୀର ଗତିରେ ଗତି କରିଥାଏ ।
(iii) ଗୋଟିଏ ବସ୍ତୁ ବିଭିନ୍ନ ସମୟରେ ଧୀର ଅଥବା ଦ୍ରୁତ ଗତିରେ ଗତି କରିଥାଏ ।
(iv) ଏକା ସମୟ ଅନ୍ତରାଳରେ ଯେଉଁ ଯାନଟି ଅଧ୍ୟା ଦୂରତା ଅତିକ୍ରମ କରେ ତାହା ଅପେକ୍ଷାକୃତ ଦ୍ରୁତତର ଗତିରେ ଯାଉଛି ବୋଲି କୁହାଯାଏ ।
→ ବେଗ :
- ଏକକ ସମୟରେ ଗୋଟିଏ ବସ୍ତୁ ଯେତିକି ଦୂରତା ଅତିକ୍ରମ କରେ, ତାହାକୁ ସେ ବସ୍ତୁର ବେଗ କୁହାଯାଏ ।

- ଯେକୌଣସି ଯାନ ଗତିଶୀଳ ଥିଲାବେଳେ ଏକ ସମାନ ବେଗରେ ଗତିକରେ ନାହିଁ । ଗତିଶୀଳ ଅବସ୍ଥାରେ ସର୍ବଦା ବେଗ କମ୍ ବା ବେଶି ହୋଇଥାଏ । ତେଣୁ ଗତିଶୀଳ ଯାନର ବେଗ ହେଉଛି ପ୍ରକୃତରେ ତାହାର ହାରାହାରି ବେଗ ।

- ଗୋଟିଏ ବସ୍ତୁ ଗତି କଲାବେଳେ ଯଦି ତାର ବେଗ ବାରମ୍ବାର ପରିବର୍ତ୍ତିତ ହୁଏ, ଏପରି ଗତିକୁ ନୈକସମାନ ବା ଅସମଗତି କୁହାଯାଏ ।
- ଯଦି କୌଣସି କ୍ଷେତ୍ରରେ ଏକ ସରଳରେଖାରେ ଗତି କରୁଥିବା ଗୋଟିଏ ବସ୍ତୁର ବେଗ ଅପରିବର୍ତ୍ତିତ ରହେ, ତେବେ ସେପରି ଗତିକୁ ସମଗତି କୁହାଯାଏ ।
- ଗୋଟିଏ ବସ୍ତୁର ବେଗ ଗଣନା କରିବା ପାଇଁ ବସ୍ତୁଟି ଗତି କରିଥିବା ମୋଟ ଦୂରତ୍ୱ ଏବଂ ସେହି ଗତି ପାଇଁ ବସ୍ତୁଟି ନେଇଥିବା ମୋଟ ସମୟ ନିର୍ଣ୍ଣୟ କରିବା ଦରକାର । `
→ ସମୟର ମାପ :
- ଗୋଟିଏ ସୂର୍ଯ୍ୟୋଦୟଠାରୁ ତା ଗୋଟିଏ ଦିନ କୁହାଯାଏ । ଗୋଟିଏ ଦିନ ଠାରୁ କମ୍ ଘଣ୍ଟା ବ୍ୟବହାର କରାଯାଏ ।
- ପୂର୍ବକାଳରେ ସମୟ ମାପିବା ଯନ୍ତ୍ର ବା ଘଡ଼ି ବ୍ୟବହାର କରାଯାଉଥିଲା ; ଯଥା – ବାଲୁକାଘଡ଼ି, ଜଳଘଡ଼ି, ସୂର୍ଯ୍ୟଘଡ଼ି ଇତ୍ୟାଦି ।

→ ସରଳ ଦୋଳକ :
- ସରଳ ଦୋଳକର୍ ସୂତାର ଦୈର୍ଘ୍ୟ ପ୍ରାୟ 1 ମିଟର । ସୂତାରୁ ଝୁଲିଥିବା ଛୋଟ, ଭାରୀ (ସାଧାରଣତଃ ଗୋଲାକାର) ବସ୍ତୁକୁ ଗୋଲକ (Bob) କୁହାଯାଏ ।
- ଦୋଳକର ବକୁ A ପାର୍ଶ୍ଵକୁ ଟାଣି ଛାଡ଼ିଦେଲେ ବର୍ଟି ଦୋଳନ କରି ମାଧ୍ୟ ଅବସ୍ଥାନ ‘O’କୁ ଅତିକ୍ରମ କରି ‘B’ ପାର୍ଶ୍ଵକୁ ଯିବ ।
- B ପାର୍ଶ୍ଵରୁ ବକ୍ଟି ଦୋଳନ କରି ମାଧ ଅବସ୍ଥାନ ଠ ଦେଇ À ପାର୍ଶ୍ଵକୁ ଫେରିବ ।
- ଏହିପରି ବବ୍ ନିରନ୍ତର ଗତିକରି ଚାଲିବ । ବତ୍ର ଏହି ଗତିକୁ ଦୋଳନ ଗତି କୁହାଯାଏ ।
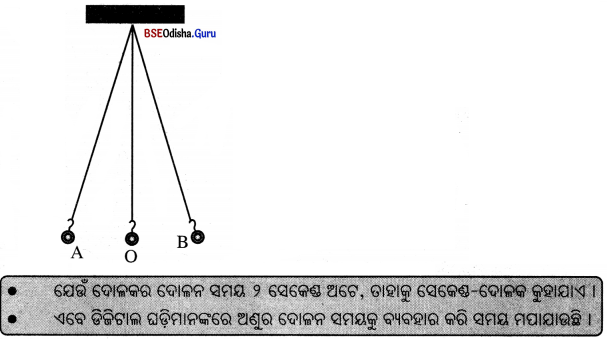
- ବଟି ସ୍ଥିତି Aରୁ ସ୍ଥିତି Bକୁ ଯାଇ ପୁଣି ସ୍ଥିତି Aକୁ ଫେରିଆସିବାକୁ ଯେତିକି ସମୟ ନିଏ ତାହା ଏହି ନିର୍ଦ୍ଦିଷ୍ଟ ସରଳ ଦୋଳକର ଦୋଳନ ସମୟ (Period of Oscillation) କୁହାଯାଏ ।
![]()
→ ସମୟର ଏକକ :
- ସମୟର ମୌଳିକ ଏକକ ସେକେଣ୍ଡ । ସମୟର ବୃହତ୍ତର ଏକକ ମିନିଟ୍ ବା ଘଣ୍ଟା ।
- ବୟସ ପ୍ରକାଶ କରିବା ପାଇଁ ବର୍ଷକୁ ଏକକ ରୂପେ ବ୍ୟବହାର କରାଯାଏ ।
→ ବେଗର ଏକକ :
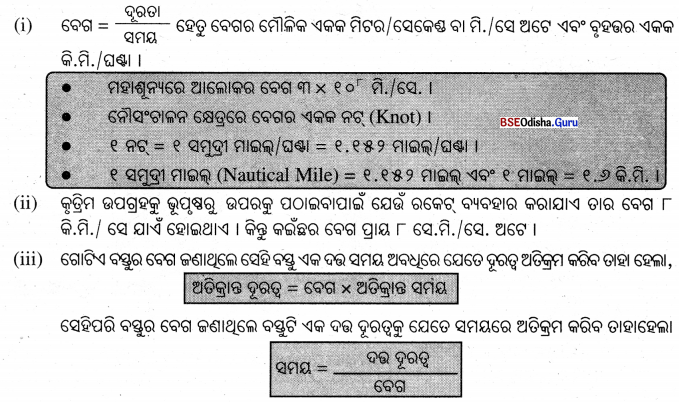
- ଗୋଟିଏ ମିଟର ଯାନର ବେଗ ଦର୍ଶାଇଥାଏ କାରଣ ସେଥିରେ କି.ମି.|ଘଣ୍ଟା ଲେଖା ହୋଇଥାଏ । ଏହି ମିଟରକୁ ବେଗ ମିଟର (Speedometer) କୁହାଯାଏ ।
- ଯାନମାନଙ୍କରେ ମିଟର ମଧ୍ୟ ଲାଗିଥାଏ ଯାହା ଯାନଟି ଯାତ୍ରା କରିଥିବା ଦୂରତ୍ୱ କିଲୋମିଟରରେ ଦର୍ଶାଇଥାଏ । ଅନେକ ସମୟରେ ବେଗ ମିଟରରେ ହିଁ ଏକ ଆୟତାକାର ଜାଗାରେ ଏହି ମିଟର ଥାଏ ଓ ତା’ ଉପରେ କି.ମି. ଲେଖା ହୋଇଥାଏ । ଏହି ମିଟରକୁ ଓଡୋମିଟର କହନ୍ତି ।
→ ଗତିଶୀଳ ବସ୍ତୁର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ :
- ଦୁଇଟି ସରଳରେଖାର ଛେଦ ବିନ୍ଦୁକୁ O ମୂଳବିନ୍ଦୁ (Origin) କୁହାଯାଏ । X’OX ଓ Y’OY କୁ ଅକ୍ଷ କୁହାଯାଏ । ମୂଳ ବିନ୍ଦୁର ଡାହାଣକୁ X- ର ମୂଲ୍ୟ ଯୁକ୍ତାତ୍ମକ ଓ ବାମକୁ ବିଯୁକ୍ତାତ୍ମକ ହୋଇଥାଏ । ସେହିପରି ମୂଳବିନ୍ଦୁରୁ ଉପରକୁ Y- ର ମୂଲ୍ୟ ଯୁକ୍ତାତ୍ମକ ଓ ତଳକୁ ବିଯୁକ୍ତାତ୍ମକ ହୋଇଥାଏ । ଗ୍ରାଫ୍ Y-ଅକ୍ଷରେ ନିଆଯାଇଥାଏ ।
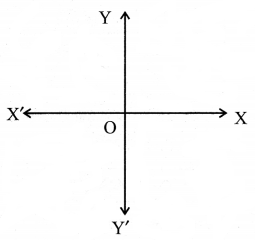
- ଗୋଟିଏ ବସ୍ତୁର ଗତିକୁ ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ଦ୍ଵାରା ଉପସ୍ଥାପନ କରାଯାଏ ।
- ଏକ ସମାନ ବେଗରେ ଗତି କରୁଥିବା ବସ୍ତୁର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ଏକ ସରଳରେଖ୍ ଗ୍ରାଫ୍ ଅଟେ ।
- ଗତିଜନିତ ଅନେକ ପ୍ରଶ୍ନ ସମାଧାନ କରିବାରେ ଗ୍ରାଫ୍ ସାହାଯ୍ୟ କରେ ।
→ ଆସ, ଜାଣିବା :
- ଏକକ ସମୟରେ ଗୋଟିଏ ବସ୍ତୁ ଗତି କରିଥିବା ଦୂରତାକୁ ବସ୍ତୁର ବେଗ କୁହାଯାଏ ଏବଂ ତାହା ମି./ସେ.ରେ ପ୍ରକାଶ କରାଯାଏ ।
- ଗୋଟିଏ ବସ୍ତୁ ଗତି କରିଥିବା ଦୂରତାକୁ ଗତି କରିଥିବା ସମୟରେ ଭାଗ କଲେ ତାହା ବସ୍ତୁର ହାରାହାରି ବେଗ ଦେଇଥାଏ । ବେଗର ମୌଳିକ ଏକକ ମି.|ସେ. ଅଟେ ।
- ବିଭିନ୍ନ ଗତିଶୀଳ ବସ୍ତୁ ମଧ୍ଯରେ କେଉଁ ଗୋଟିକ କ୍ଷିପ୍ରତର ବା କ୍ଷିପ୍ରତମ ଜାଣିବାରେ ଆମକୁ ବେଗ ସାହାଯ୍ୟ କରିଥାଏ ।
- ସମୟ ମାପିବା ପାଇଁ ଦୋଳନ ପ୍ରକ୍ରିୟା ବ୍ୟବହାର କରାଯାଏ । ସରଳ ଦୋଳକର ଦୋଳନ ଗତି ବ୍ୟବହାର କରି ଘଣ୍ଟା ସାଧାରଣତଃ ତିଆରି କରଯାଏ ।
- ଗୋଟିଏ ବସ୍ତୁର ଗତିକୁ ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ଦ୍ବାରା ଉପସ୍ଥାପନ କରାଯାଏ ।
- ଏକ ସମାନ ବେଗରେ ଗତି କରୁଥିବା ବସ୍ତୁର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ଏକ ସରଳରେଖ୍ ଗ୍ରାଫ୍ ଅଟେ ।
