Odisha State Board BSE Odisha 8th Class Maths Notes Algebra Chapter 4 ଉତ୍ପାଦକୀକରଣ will enable students to study smartly.
BSE Odisha Class 8 Maths Notes Algebra Chapter 4 ଉତ୍ପାଦକୀକରଣ
→ ଉପକ୍ରମଣିକା (Introduction) :
ଗଣନ ସଂଖ୍ୟା ବା ସ୍ଵାଭାବିକ ସଂଖ୍ୟାକୁ କେତେକ ମୌଳିକ ସଂଖ୍ୟାର ଗୁଣନୀୟକ ଭାବେ ପରିଣତ କରିବାର ପ୍ରଣାଳୀକୁ ଉତ୍ପାଦକୀକରଣ କୁହାଯାଏ ।
→ ଉତ୍ପାଦକ ଏବଂ ଉତ୍ପାଦକୀକରଣ (Factors and Factorisation):
ସହ ସମାନ ହେଲେ, ଉକ୍ତ ସଂଖ୍ୟା ଏବଂ ଉତ୍ପନ୍ନ ରାଶିମାନଙ୍କୁ ଦତ୍ତ ରାଶିର ଗୋଟିଏ ଗୋଟିଏ ଉତ୍ପାଦକ କୁହାଯାଏ ।
ଉଦାହରଣ : 3xy = 3 × x × x × y
ଏଠାରେ 3xy ର 3, x, x ଏବଂ y ଗୋଟିଏ ଗୋଟିଏ ଗୁଣନୀୟକ ବା ଉତ୍ପାଦକ ।
ଉଦାହରଣ : 30 = 1 × 30 = 2 × 15 = 3 × 10 = 5 × 6 = 2 × 3 × 5
(i) କୌଣସି ମୌଳିକ ସଂଖ୍ୟାକୁ ଅନନ୍ୟ ଭାବେ କେତେକ ମୌଳିକ ସଂଖ୍ୟାର ଗୁଣନୀୟକ ଭାବେ ପ୍ରକାଶ କରାଯାଏ; ଅର୍ଥାତ୍ 30 = 2 × 3 × 5
(ii) ଉତ୍ପାଦକୀକରଣ ଏକ ପ୍ରକ୍ରିୟା, ଯେଉଁଥରେ ଦତ୍ତ ବୀଜଗାଣିତିକ ରାଶିକୁ କେବଳ ମୌଳିକ ସଂଖ୍ୟା ବା ମୌଳିକ
→ ବଣ୍ଟନ ନିୟମ ବ୍ୟବହାର କରି ଉତ୍ପାଦକ ବିଶ୍ଳେଷଣ :
(i) ପରିମେୟ ସଂଖ୍ୟା ସେଟ୍ରେ ବଣ୍ଟନ ନିୟମଟି ହେଲା –
x (a + b) = xa + bx ବା xa + xb = x (a + b)
ଏଠାରେ x (a + b) ପରିପ୍ରକାଶର x ଏକ ଉତ୍ପାଦକ ଓ a + b ଅନ୍ୟ ଏକ ଉତ୍ପାଦକ ।
(ii) ବଣ୍ଟନ ନିୟମ ଦୁଇରୁ ଅଧୂକ ପଦବିଶିଷ୍ଟ ରାଶି ପାଇଁ ମଧ୍ୟ ପ୍ରଯୁଜ୍ୟ ।
xa + xb + xc = x(a + b + c)
![]()
ମନେରଖ :
- ପଦମାନଙ୍କର କୌଣସି ସାଧାରଣ ଗୁଣନୀୟକ ନଥିଲେ, ଏ ପ୍ରଣାଳୀ ପ୍ରଯୁଜ୍ୟ ହେବ ନାହିଁ ।
- ଦ୍ବିପଦ, ତ୍ରିପଦ ବା ବହୁପଦ ବିଶିଷ୍ଟ ରାଶି ମଧ୍ୟ ଗୁଣନୀୟକ ହୋଇପାରେ ।
- ସାଧାରଣ ଗୁଣନୀୟକ, ଗୋଟିଏ ସଂଖ୍ୟା ବା ବୀଜଗାଣିତିକ ସଂକେତ; ଯଥା – a, b, c, x, y, z ଇତ୍ୟାଦି ହୋଇପାରେ ।
ଉଦାହରଣ :
4x + 8 କୁ ଉତ୍ପାଦକରେ ବିଶ୍ଳେଷଣ କର ।
ସମାଧାନ :
4x + 8 = 4 (x + 2)
ଉଦାହରଣ :
x²yx + xy²z + xyz² କୁ ଉତ୍ପାଦକରେ ବିଶ୍ଳେଷଣ କର ।
ସମାଧାନ :
x²yx + xy²z + xyz² = x × y × z (x + y + z) = xyz (x + y + z)
→ ପଦଗୁଡ଼ିକୁ ଦୁଇ ବା ତତୋଽଧ୍ଵକ ଭାଗରେ ବିଭକ୍ତ କରି ଉତ୍ପାଦକ ନିର୍ଣ୍ଣୟ (Factorisation by grouping method) :
ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶକୁ ଏପରି ଦୁଇ ବା ତତୋଽଧ୍ଵ ଭାଗରେ ବିଭକ୍ତ କରାଯିବ, ଯେପରି ପ୍ରତ୍ୟେକ ଆବଶ୍ୟକସ୍ଥଳେ ପଦଗୁଡ଼ିକୁ ପୁନଃସଜିକରଣ କରାଯାଇ ଉତ୍ପାଦକ ନିର୍ଣ୍ଣୟ କରିବାକୁ ହେବ ।
ଉଦାହରଣ :
x² – xy – xz + yz ର ଉତ୍ପାଦକ ବିଶ୍ଳେଷଣ କର ।
ସମାଧାନ :
x² – xy – xz + yz = x(x – y) – z (x – y) = (x – y) (x – z)
→ ଦ୍ଵିଘାତ ପଲିନୋମିଆଲର ଉତ୍ପାଦକୀକରଣ ପ୍ରଣାଳୀ :
ଦ୍ଵିଘାତ ପଲିନୋମିଆଲର ସାଧାରଣ ରୂପ ହେଉଛି x² + px + q ।
ଏହାର ମଧ୍ୟମ ପଦ px କୁ ଯେଉଁଥରେ x ଚଳରାଶି ଓ p ସହଗ ଏବଂ ଉଭୟ p ଓ q ପ୍ରତ୍ୟେକ ଧ୍ରୁବକ ପଦ ।
(i) ଦ୍ବିଘାତ ପରିପ୍ରକାଶକୁ ଅଜ୍ଞାତ ରାଶିର ଘାତର ଅଧଃକ୍ରମରେ ସଜାଇ ରଖୁବାକୁ ହେବ ।
(ii) ଏପରି ଦୁଇଟି ସଂଖ୍ୟା ନିର୍ଣ୍ଣୟ କରିବାକୁ ହେବ, ଯାହାର ଯୋଗଫଳ ମଧ୍ୟମ ପଦର ସହଗ ସହ ସମାନ ଓ ଗୁଣଫଳ ତୃତୀୟ ପଦ ସହ ସମାନ ହେବ ।
(iii) ଏହାପରେ ମଧ୍ୟମ ପଦଟିକୁ ଆବଶ୍ୟକତା ଅନୁଯାୟୀ ଦୁଇଟି ପଦରେ ପ୍ରକାଶ କରିହେବ ।
(iv) ବର୍ତ୍ତମାନ ଚାରିପଦ ବିଶିଷ୍ଟ ରାଶିକୁ ଉତ୍ପାଦକରେ ବିଶ୍ଳେଷଣ କରିବା ।
ଉଦାହରଣ :
ଉତ୍ପାଦକରେ ବିଶ୍ଳେଷଣ କର ।
(i) x² + 5x + 6
(ii) x² – 5x + 6
ସମାଧାନ :
(i) x² + 5x + 6 କୁ x² + px + q ରେ ପ୍ରକାଶକଲେ p = 5 ଓ q = 6 ହେବ ।
5 କୁ ଦୁଇଟି ପଦରେ ଭାଙ୍ଗିବାକୁ ହେବ, ଯେପରି ଏହାର ଯୋଗଫଳ 5 ଓ ଗୁଣଫଳ 6 ହେବ ।
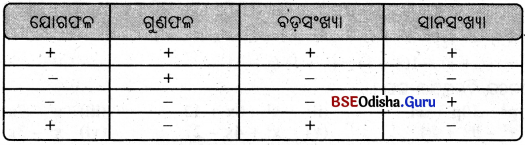
ଏଠାରେ ଗୁଣଫଳ ଧନାତ୍ମକ ହୋଇଥିବାରୁ, ଯୋଗ ବା ମିଶାଣଫଳ ମଧ୍ୟ ଧନାତ୍ମକ ।
x² + 5x + 6 = x² + (3 + 2)x + 3 × 2
= x² + 3x + 2x + 6 = x(x + 3) + 2(x + 3) = (x + 3) (x + 2)
(ii) x² – 5x + 6 ଏଠାରେ p = -5 ଓ q = 6
x² + (-5)x + 6 = x² + {(3) + (-2) }x + (-3)(-2) = x² – 3x – 2x + 6
= x(x – 3) – 2(x – 3) = (x – 3) (x – 2)
![]()
ମନେରଖ :
→ ବିଭିନ୍ନ ଅଭେଦ ସାହାଯ୍ୟରେ ଉତ୍ପାଦକ ନିର୍ଣ୍ଣୟ (Factorisation using different Identities) :
ଉତ୍ପାଦକ ବିଶ୍ଳେଷଣରେ ଆବଶ୍ୟକ ଅଭେଦାବଳୀ ନିମ୍ନରେ ଦତ୍ତ ଅଛି ।
(i) a² + 2ab + b² = (a + b)²
(ii) a² – 2ab + b² =(a – b)²
(iii) a² – b² = (a + b)(a – b)
(iv) a² + b² + c² + 2ab + 2bc + 2ca = (a + b + c)²
(v) a² + b² + c² – 2ab – 2bc + 2ca = (a – b + c)²
(vi) a² + b² + c² + 2ab – 2bc – 2ca = (a + b – c)²
(vii) a² + b² + c² – 2ab + 2bc – 2ca = (a – b – c)²
