BSE Odisha 8th Class Maths Notes Algebra Chapter 5 ସୂଚକ ତତ୍ତ୍ଵ

Odisha State Board BSE Odisha 8th Class Maths Notes Algebra Chapter 5 ସୂଚକ ତତ୍ତ୍ଵ will enable students to study smartly.

BSE Odisha Class 8 Maths Notes Algebra Chapter 5 ସୂଚକ ତତ୍ତ୍ଵ

→ ଉପକ୍ରମଣିକା (Introduction):
ଆମେ ଜାଣିଛେ 5 × 5 × 5 = 5³, ଯେଉଁଠାରେ 5 ଏକ ଘାତରାଶି ଏବଂ 5 ଓ 3 ଯଥାକ୍ରମେ ଘାତରାଶିର ଅଧାର ଏବଂ ଘାତ । ସେହିପରି (-2) × (-2) × (- 2) × (2) = (-2)⁴ । ଏଠାରେ ମଧ୍ୟ (- 2) ଏକ ଘାତରାଶି ଏବଂ -2⁴ ଓ 4 ଯଥାକ୍ରମେ ଘାତରାଶିର ଆଧାର ଓ ଘାତ ।

• a × a × a × ……. m ଥର ଗୁଣିଲେ = a^m ଲେଖାଯାଏ, ଯେଉଁଠାରେ a ଏକ ପୂର୍ଣ୍ଣସଂଖ୍ୟା ଅଥବା ପରିମେୟ ସଂଖ୍ୟା ଏବଂ m ଏକ ଗଣନ ସଂଖ୍ୟା । a^m ଏକ ଘାତରାଶି ଏବଂ a ଓ m ଯଥାକ୍ରମେ ଘାତରାଶିର ଆଧାର ଓ ଘାତାଙ୍କ ।

→ ଧନାତ୍ମକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା (ଗଣନ ସଂଖ୍ୟା) ଘାତାଙ୍କ ବିଶିଷ୍ଟ ଘାତରାଶି :
ପ୍ରତ୍ୟେକ ଘାତରାଶି (ଗଣନ ସଂଖ୍ୟା ଘାତାଙ୍କ ବିଶିଷ୍ଟ)ର ମାନ ଥାଏ ।
ଯୋପରି 2³ = 2 × 2 × 2 = 8, (-4)² = (-4) × (-4) = 16,

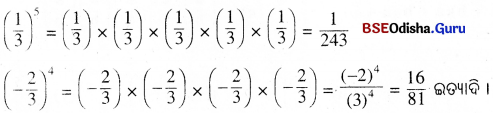
ନିଜେ କର :

Question 1.
ନିମ୍ନଲିଖ ସଂଖ୍ୟାକୁ ଘାତରାଶିରେ ପରିଣତ କର ।
(a) 625
(b) -27
(c) 243
(d) 1000
(e) \(\frac{4}{9}\)
ଉତ୍ତର –
(a) 625 = 5 × 5 × 5 × 5 = (5)⁴
(b) (-27) = (-3) × (-3) × (-3) = (-3)³
(c) 243 = 3 × 3 × 3 × 3 × 3 = (3)⁵
(d)1000 = 10 × 10 × 10 = (10)³
(e) \(\frac{4}{9}=\frac{2}{3} \times \frac{2}{3}=\left(\frac{2}{3}\right)^2\)

Question 2.
ନିମ୍ନ ଘାତ ରାଶିଗୁଡ଼ିକର ମାନ ସ୍ଥିର କର ।
(a) 6³
(b) (-8)³
(c) (12)²
(d) (-11)³
(e) \((- \frac{1}{5})^3\)
ଉତ୍ତର –
(a) 6³ = 6 × 6 × 6 = 216
(b) (-8)³ = (-8) × (-8) × (-8) = -512
(c) (12)² = 12 × 12 = 144
(d) (-11) = (-11) × (-11) × (-11) = -1331
(e) \(\left(-\frac{1}{5}\right)^3=\left(-\frac{1}{5}\right) \times\left(-\frac{1}{5}\right) \times\left(-\frac{1}{5}\right)=\frac{-1}{125}\)

→ ଘାତରାଶିମାନଙ୍କର ଗୁଣନ ଓ ଭାଗକ୍ରିୟା :
ନିୟମ 1 :
‘a’ ଏକ ଅଣଶୂନ୍ୟ ପରିମେୟ ସଂଖ୍ୟା ଏବଂ m ଓ n ଦୁଇଟି ଗଣନ ସଂଖ୍ୟା ହେଲେ, a^m × aⁿ = a^m+n

ଉଦାହରଣ – 1 :
2³ × 2⁴କୁ ଏକ ଘାତରାଶିରେ ପ୍ରକାଶ କର ।
ସମାଧାନ :
2³ × 2⁴ = 2³⁺⁴ = 2⁷ ……. ନିୟମ (1)

ଉଦାହରଣ 2 :
\(\left(\frac{2}{3}\right)^2 \times\left(\frac{2}{3}\right)^3\) କୁ ଏକ ଘାତରାଶିରେ ପ୍ରକାଶ କର ।
ସମାଧାନ :
\(\left(\frac{2}{3}\right)^2 \times\left(\frac{2}{3}\right)^3=\left(\frac{2}{3}\right)^3+2=\left(\frac{2}{3}\right)^5\) ………… ନିୟମ (1)

ନିୟମ – 2 :
(i) ‘a’ ଏକ ଅଣଶୂନ୍ୟ ପରିମେୟ ସଂଖ୍ୟା ଏବଂ m ଓ n ଦୁଇଟି ଗଣନ ସଂଖ୍ୟା (m > n) ହେଲେ,
a^m ÷ aⁿ = a^m-n

(ii) ‘a’ ଏକ ଅଣଶୂନ୍ୟ ପରିମେୟ ସଂଖ୍ୟା ଏବଂ m ଓ n ଦୁଇଟି ଗଣନ ସଂଖ୍ୟା (n > m) ହେଲେ,
a^m ÷ aⁿ = \(\frac{1}{a^n-m}\)

ଉଦାହରଣ 3 :
\(\left(\frac{4}{3}\right)^7 \div\left(\frac{4}{3}\right)^4\) କୁ ଏକ ଘାତରାଶିରେ ପ୍ରକାଶ କର ।
ସମାଧାନ :
\(\left(\frac{4}{3}\right)^7 \div\left(\frac{4}{3}\right)^4=\left(\frac{4}{3}\right)^{7-4}=\left(\frac{4}{3}\right)^3\) ………………. ନିୟମ 2(i)

ନିୟମ – 3 :
‘a’ ଏକ ଅଣଶୂନ୍ୟ ପରିମେୟ ସଂଖ୍ୟା ଏବଂ m ଓ n ଦୁଇଟି ଗଣନ ସଂଖ୍ୟା ହେଲେ, (a^m)ⁿ = a^mn ହେବ ।

ଉଦାହରଣ 4 :
\(\left(\frac{4}{3}\right)^2 \div\left(\frac{4}{3}\right)^5\)କୁ ଘାତରାଶିରେ ପ୍ରକାଶ କର ।
ସମାଧାନ :
\(\left(\frac{4}{3}\right)^2 \div\left(\frac{4}{3}\right)^5=\frac{1}{\left(\frac{4}{3}\right)^{5-2}}=\frac{1}{\left(\frac{4}{3}\right)^3}\) ………….. ନିୟମ 2(ii)

ଉଦାହରଣ 5 :
\(\left\{\left(\frac{2}{3}\right)^3\right\}^2\)କୁ ଘାତରାଶିରେ ପ୍ରକାଶ କର ।
ସମାଧାନ :
\(\left\{\left(\frac{2}{3}\right)^3\right\}^2=\left(\frac{2}{3}\right)^{3 \times 2}=\left(\frac{2}{3}\right)^6\)

ନିୟମ – 4 :
‘a’ ଓ b ଦୁଇଟି ଅଣଶୂନ୍ୟ ପରିମେୟ ସଂଖ୍ୟା ଏବଂ ‘m’ ଏକ ଗଣନ ସଂଖ୍ୟା ହେଲେ,
(a × b)^m = a^m × b^m ହେବ ।

ଉଦାହରଣ 6 :
\(\left(\frac{3}{4}\right)^2 \times\left(\frac{5}{3}\right)^2\)କୁ ଘାତରାଶିରେ ପ୍ରକାଶ କର ।
ସମାଧାନ :
\(\left(\frac{3}{4}\right)^2 \times\left(\frac{5}{3}\right)^2=\left(\frac{3}{4} \times \frac{5}{3}\right)^2=\left(\frac{5}{4}\right)^2\)

ଉଦାହରଣ 6 :
\(\left(\frac{5}{7}\right)^3 \div\left(\frac{5}{7}\right)^3=\left(\frac{5}{7} \div \frac{5}{7}\right)^2=(1)^3=1\)
ସମାଧାନ :
\(\frac{1}{2}\)

ମନେରଖ :

• m ଏକ ଯୁଗ୍ମ ଗଣନ ସଂଖ୍ୟା ହେଲେ, (- 1)^m = 1
• m ଏକ ଅଯୁଗ୍ମ ଗଣନ ସଂଖ୍ୟା ହେଲେ, (- 1)^m = – 1

→ ପୂର୍ବ ସଂଖ୍ୟା ଘାତାଙ୍କ ବିଶିଷ୍ଟ ରାଶି :
ଆମେ ଜାଣିଛେ a³, 3 ସଂଖ୍ୟକ aର ଗୁଣଫଳ ।
ସେହିପରି a°, 0 ସଂଖ୍ୟକ ଥର ଗୁଣଫଳ ଓ a^-2, – 2 ସଂଖ୍ୟକ aର ଗୁଣଫଳ ଯାହାକି ଉକ୍ତିଦ୍ବୟ ଅର୍ଥହୀନ ।
ତେଣୁ ଆମେ a ଓ a2 ଭଳି ଘାତରାଶିର ସଂଜ୍ଞା ନିମ୍ନ ମତେ ପ୍ରକରଣ କରିବା ।
ସଂଜ୍ଞା : a° = 1, a ∈ Q, a ≠ 0
a^-n = \(\frac{1}{a^n}\), a ∈ Q, a ≠ 0, n ∈ N

ମନେରଖ :
0° ସଂଜ୍ଞାକୃତ ନୁହେଁ,
ଅନୁସିଦ୍ଧାନ୍ତ – 1 :
aⁿ × a^-n = 1 (a ≠ 0, a ∈ Q, n ∈ N)

ଅନୁସିଦ୍ଧାନ୍ତ – 2 :
1 ÷ a^-n = aⁿ (a ≠ 0, a ∈ Q, n ∈ N)

→ ପରିମେୟ ଘାତାଙ୍କ ବିଶିଷ୍ଟ ରାଶି :
n ଏକ ପରିମେୟ ସଂଖ୍ୟା ହେଲେ, aର ସଂଜ୍ଞା ପ୍ରକରଣ କରାଯାଇ ପାରିବ । (ଏଠାରେ ମନେରଖୁବାକୁ ହେବ ଯେ, a ଏକ ପରିମେୟ ସଂଖ୍ୟା ।)

ମନେରଖ :
a ∈ Q ଓ a > 0 । ଯଦି n ଏକ ଗଣନ ସଂଖ୍ୟା ହୁଏ; ତେବେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମେୟ ସଂଖ୍ୟା x ଅଛି; ଯେପରିକି xⁿ = a

ଏଠାରେ xକୁ ଆମେ \(\sqrt[n]{a}\) ବା \(a^\frac{1}{n}\) ରୂପେ ଲେଖୁରିବା ଓ ଏହାକୁ ଥର n-ତମ ମୂଳ କହୁ ।

xⁿ= a ⇒ x = \(a^\frac{1}{n}\) ବା \(\sqrt[n]{a}\), (a > 0) ଫଳରେ \(a^\frac{1}{n}\) = \(\sqrt[n]{a}\)

ଏଠାରେ \(\sqrt[n]{a}\) ଏକ ପରିମେୟ ସଂଖ୍ୟା ସଦାବେଳେ ହୋଇପାରେ ।

ଉଦାହରଣସ୍ୱରୂପ : a⁵ = 32 ହେଲେ, a = \(\sqrt[5]{32}\) ବା \((32)^{\frac{1}{3}}\) ଅର୍ଥାତ୍ 32ର ପଞ୍ଚମ ମୂଳ a = 2,

• a^m × aⁿ = a^m+n a, b > 0.
• a^m ÷ aⁿ = a^m-n a, b ∈ Q.
• (a^m)ⁿ = a^mn m, n ∈ Q.
• (ab)^m = a^m × b^m ଏବଂ \(\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}\)

ଉଦାହରଣ :
\(\left(\frac{32}{243}\right)^{\frac{2}{5}}\) କୁ ପରିମେୟ ସଂଖ୍ୟାରେ ପ୍ରକାଶ କର ।
ସମାଧାନ :
\(\left(\frac{32}{243}\right)^{\frac{2}{5}}=\left\{\left(\frac{2}{3}\right)^5\right\}^{\frac{2}{3}}=\left(\frac{2}{3}\right)^{5 \times \frac{2}{3}}=\left(\frac{2}{3}\right)^2=\frac{4}{9}\)

ଉଦାହରଣ :
ସରଳ କର : (0.4)² × \((0.125)^\frac{1}{3}\) ÷ \((2 \frac{1}{2})^-3\)
ସମାଧାନ :