BSE Odisha 8th Class Maths Notes Geometry Chapter 5 ପରିମିତି

Odisha State Board BSE Odisha 8th Class Maths Notes Geometry Chapter 5 ପରିମିତି will enable students to study smartly.

BSE Odisha Class 8 Maths Notes Geometry Chapter 5 ପରିମିତି

→ ପିଥାଗୋରାସ୍‌ଙ୍କ ଉପପାଦ୍ୟ ଓ ଏହାର ପ୍ରୟୋଗ :
(A) ସମକୋଣୀ ତ୍ରିଭୁଜ ।

• △ABCର ∠B ସମକୋଣ ଓ \(\overline{\mathrm{AC}})\) କର୍ଣ୍ଣ (hypotenuse) । ∠Bର ସଂଲଗ୍ନ ବାହୁଦ୍ଵୟ AB ଓ BC ମଧ୍ୟରୁ BC କୁ ଭୂମି (base) ଓ AB କୁ ଲମ୍ବ (perpendicular) କୁହାଯାଏ । ଲମ୍ବର ଦୈର୍ଘ୍ୟକୁ ତ୍ରିଭୁଜର ଉଚ୍ଚତା (height) କୁହାଯାଏ ।
• ସମକୋଣୀ ତ୍ରିଭୁଜର ଉଚ୍ଚତା, ଭୂମିର ଦୈର୍ଘ୍ୟ ଓ କଣ୍ଠର ଦୈର୍ଘ୍ୟକୁ p, b ଓ h ଦ୍ଵାରା ସୂଚିତ କରାଯାଏ ।
  
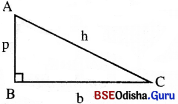
• ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟର ବର୍ଗ ଏହାର ଅନ୍ୟ ଦୁଇବାହୁର ଦୈର୍ଘ୍ୟର ବର୍ଗର ସମଷ୍ଟି ସହ | h² = p² + b²

→ ପିଥାଗୋରାଯ ତ୍ରଯି (Pythagorean Triple)
ABC ସମକୋଣୀ ଧର m∠B = 90° ହେଲେ,
AC² = AB² + BC²
h² = p² + b² କିମ୍ବା h = \(\sqrt{\mathrm{p}^2+\mathrm{b}^2}\)
p² = h² + b² କିମ୍ବା p = \(\sqrt{\mathrm{h}^2-\mathrm{b}^2}\)
b² = h² + p² କିମ୍ବା b = \(\sqrt{\mathrm{h}^2-\mathrm{p}^2}\)

ସମକୋଣୀ ତ୍ରିଭୁଜର ଦାହୁମାନକ ମଧ୍ୟରେ ଥିବା ସମକ p² + b²‍ = h², ଯେଉଁ ତିନଟିକିଆ ଗଣନ ସଂଖ୍ୟା ଗୋଷ୍ଠୀଦ୍ଵାରା ସିଦ୍ଧ ହୁଏ, ତାହାକୁ ପିଥାଗୋରୀୟ ତ୍ରୟୀ ଅଥବା ପିଥାଗୋରୀୟ ଟ୍ରିପିଲ୍ କୁହାଯାଏ ।

• ମନେରଖ : (3, 4, 5) (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41) ଏହି ତ୍ରୟୀଗୁଡ଼ିକ ପରସ୍ପର ମୌଳିକ । ତେଣୁ ଉପରୋକ୍ତ ତ୍ରୟିଗୁଡ଼ିକୁ ମୌଳିକ ପିଥାଗୋରୀୟ ତ୍ରୟୀ କୁହାଯାଏ ।

→ କ୍ଷେତ୍ର ଓ କ୍ଷେତ୍ରଫଳ (Region and Area) :

• ଗୋଟିଏ ତ୍ରି ଭୁଜ ଓ ଏହାର ଅନ୍ତର୍ଦେଶର ସପୋଗରେ ହିରୁକାକୃତି ବିଶିପ କ୍ଷେତ୍ର ଗଠିତ ହୁଏ ।
• କ୍ଷେତ୍ରର ମାପକୁ କ୍ଷେତ୍ରଫଳ (Area) କୁହାଯାଏ ।
  

→ କ୍ଷେତ୍ରଫଳ (Area) ସମ୍ବନ୍ଧୀୟ ସ୍ଵୀକାର୍ଯ୍ୟ :
ସ୍ଵୀକାର୍ଯ୍ୟ – 1 : ପ୍ରତ୍ୟେକ ବହୁଭୁଜଦ୍ୱାରା ଆବଦ୍ଧ କ୍ଷେତ୍ର (closed region)ର ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ କ୍ଷେତ୍ରଫଳ ଅଛି । ଏହା ଏକ ଧନାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା ।
ସ୍ଵୀକାର୍ଯ୍ୟ – 2 : ଗୋଟିଏ ବହୁଭୁଜଦ୍ୱାରା ବିଶିଷ୍ଟ କ୍ଷେତ୍ରମାନଙ୍କର କ୍ଷେତ୍ରଫଳର ସମଷ୍ଟିସହ ସମାନ ।

→ କ୍ଷେତ୍ରଫଳର ମାପ :

• ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ l ଏକକ ଓ ପ୍ରସ୍ଥ b ଏକକ ହେଲେ, କ୍ଷେତ୍ରଫଳ = (l × b) ବର୍ଗ ଏକକ
• ବର୍ଗକ୍ଷେତ୍ରର ବାହୁ a ଏକକ ହେଲେ, କ୍ଷେତ୍ରଫଳ = a² ବର୍ଗ ଏକକ
• ସମକୋଣ ତ୍ରିଭୁଜର ଯେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × ସମକୋଣସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ ।

→ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ :

• ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) ଭୂମିର ଦୈର୍ଘ୍ୟ × ଉଚ୍ଚତା
• ଭୂମିର ଦୈର୍ଘ୍ୟ = \(\frac { 2 × କ୍ଷେତ୍ରଫଳ }{ ଉଚ୍ଚତା }\) ଏବଂ ଉଚ୍ଚତା = \(\frac { 2 × କ୍ଷେତ୍ରଫଳ }{ ଭୂମିର ଦୈର୍ଘ୍ୟ }\)
• ସମକୋଣୀ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × ସମକୋଣଲଗ ବାହଦ୍ୱପର ଗ୍ମଣପଲ |
• ସମଦାଦୁ ତ୍ରିଭୁଜର ପ୍ରତତ୍ୟକ ଦାଦୁର ଶେଶ୍ୟ a ଏକକ ଦୈର୍ଘ୍ୟର = \(\frac{\sqrt{3}}{4}\) a² ବର୍ଗ ଏକକ ।
• ଉଚ୍ଚତା ଦତ୍ତ ଥିଲେ, ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{\sqrt{3}}\) (ଉଚ୍ଚତା)²
• ବିଷମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\sqrt{s(s-a)(s-b)(s-c)}\) ବର୍ଗ ଏକକ (s = ଅର୍ଥପରିସୀମା)

ଏହା ହେରଙ୍କ ସୂତ୍ର ଭାବରେ ପରିଚିତ ।

କ୍ଷେତ୍ରଫଳ ମାପର ପ୍ରଚଳିତ ଏକକ :

→ ସାମାନ୍ତରିକକ୍ଷେତ୍ର ଓ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ :
(କ) ସାମାନ୍ତରିକକ୍ଷେତ୍ର :

• ବିପରୀତ ବାହୁଗୁଡ଼ିକର ଦୈର୍ଘ୍ୟ ସମାନ୍ତର ଓ ସମାନ ।
• ବିପରୀତ କୋଣମାନଙ୍କର ପରିମାଣ ସମାନ ।
• କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।
• ପ୍ରତ୍ୟେକ କର୍ଣ୍ଣ ଉପରେ ଏହାର ଉଭୟ ପାର୍ଶ୍ଵରେ ଥ‌ିବା କୌଣିକ ବିଦୁ୍ୟଦ୍ୱୟରୁ ଅଙ୍କିତ ଲମ୍ବନ୍ଵୟର ଦୈର୍ଘ୍ୟ ସମାନ ।
• ପ୍ରତ୍ୟେକ କର୍ଷ ସାମାନ୍ତରିକକ୍ଷେତ୍ରକୁ ଦୁଇଟି ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ତ୍ରିଭୁଜରେ ବିଭକ୍ତ କରେ ।
• ଦୁଇଟି କଣ୍ଠଦ୍ଵାରା କ୍ଷେତ୍ରଟି ଚାରିଗୋଟି ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ତ୍ରିଭୁଜରେ ବିଭକ୍ତ ହୁଏ ।
• ବର୍ଗକ୍ଷେତ୍ର, ଆୟତକ୍ଷେତ୍ର ଓ ରମ୍ବସ୍ ଆକୃତି ବିଶିଷ୍ଟ କ୍ଷେତ୍ର ମଧ୍ୟ ଗୋଟିଏ ଗୋଟିଏ ସାମାନ୍ତରିକକ୍ଷେତ୍ର ।

ସାମାନ୍ତରିକକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ :

ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ଓ ସେଦ୍ଵି ଦାହ୍ମ ପ୍ରତି ରଲତା ଦର ଥିଲେ
ସାମାନ୍ତରିକକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଏକ ଦାଦିତ ବେଶ୍ୟ × ସେହ ଦାହସୃତି ଅନିତ କକଡା |

ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ଓ ଏହାର ସମ୍ମୁଖୀନ ଯେକୌଣସି ବିନ୍ଦୁରୁ ଏହା ପ୍ରତି ଲମ୍ବର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ,

ସାମାନ୍ତରିକକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଗୋଟିଏ କଣ୍ଠର ଦୈର୍ଘ୍ୟ × ଏହି କଣ୍ଠ ଉପରେ ଏହାର ସମ୍ମୁଖୀନ ଏକ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ ।

ଗୋଟିଏ ବାହୁ ଓ କର୍ଣ୍ଣଦ୍ଵୟର ଛେଦବିନ୍ଦୁରୁ ସେହି ବାହୁ ଉପରେ ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ,
ସାମାନ୍ତରିକକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 2 × ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ × କଣ୍ଠଦ୍ଵୟର ଛେଦବିନ୍ଦୁରୁ ସେହି ବାହୁ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ ।

ଦୁଇଟି ସନ୍ନିହିତ ବାହୁ ଓ ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ,
ସାମାନ୍ତରିକକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = \(2 \sqrt{s(s-a)(s-b)(s-c)}\) ଯେଉଁଠାରେ s = \(\frac { a + b + c }{ 2 }\)

କର୍ଣ୍ଣଦ୍ଵୟ ଓ ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ,
ABCD ସାମାନ୍ତରିକକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 4 × △OBCର କ୍ଷେତ୍ରଫଳ ।

→ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ
ଯେଉଁ ଚତୁର୍ଭୁଜର କେବଳ ଏକଯୋଡ଼ା ବିପରୀତ ବାହୁ ପରସ୍ପର ସମାନ୍ତର, ସେହି ଚତୁର୍ଭୁଜକୁ ଟ୍ରାପିଜିୟମ୍ କୁହାଯାଏ ।

ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac {1 }{ 2 }\) × ସମାନ୍ତର ଦତ୍ତଦ୍ୱୟର ଶେଷ୍ୟ ସମସ୍ତ × ଉଚ୍ଚତା
= ଅସମାନ୍ତର ବାୟୁଦ୍ଵୟର ମଧ୍ୟବିନ୍ଦୁର ସଂଯୋଜକ ରେଖାଖଣ୍ଡର ଦୈର୍ଘ୍ୟ × ଉଚ୍ଚତା

→ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ :
ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ ଏବଂ ସେହି କଣ୍ଠପ୍ରତି ତାହାର ସମ୍ମୁଖୀନ କୌଣିକ ବିଦୁ୍ୟଦ୍ୱୟରୁ ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ,
ତତ୍ରୁଭୁକର ଶେତ୍ରଫଳ = \(\frac {1 }{ 2 }\) × ଗୋଟିଏ କଣ୍ଠର ଦୈର୍ଘ୍ୟ × ଉକ୍ତ କଣ୍ଠର ସମ୍ମୁଖୀନ କୌଣିକ ବିଦୁ୍ୟଦ୍ୱୟରୁ ସେହି କଣ୍ଠପ୍ରତି ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି ।

ପରସ୍ପରପ୍ରତି ଲମ୍ବ ହୋଇଥିବା କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ,
ତତ୍ରୁଭୁକର ଶେତ୍ରଫଳ = \(\frac {1 }{ 2 }\) × କଣ୍ଠଦମ୍ନର ଦେଖ୍ୟ ଗୁଣଫଳ |

ଏକ ସ୍ଵତନ୍ତ୍ରପ୍ରକାର ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ :
ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac {1 }{ 2 }\) ବହିଃସ୍ଥ କଣ୍ଠର ଦୈର୍ଘ୍ୟ × ଉକ୍ତ କଣ୍ଠ ଉପରେ ସେହି କଣ୍ଠର ସମ୍ମୁଖୀନ ଶୀର୍ଷବିନ୍ଦୁଦ୍ଵୟରୁ ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟର ବିୟୋଗଫଳ ।

→ ଘନପଦାର୍ଥ ଏବଂ ଏହାର ଆକୃତି :

ସମଘନ, ଆୟତଘନ, ପ୍ରିଜିମ୍, ସିଲିଣ୍ଡର, କୋହ୍ଲ, ଗୋଲକ ଆଦି ବସ୍ତୁଗୁଡ଼ିକୁ ଏକ ସମତଳରେ ରଖିଲେ ଏହାର ଗୋଟିଏ ପାର୍ଶ୍ଵ ବା ଏହାର କିଛି ଅଂଶ ସମତଳରେ ରହି ଅନ୍ୟ ଅଂଶ ବା ପାର୍ଶ୍ଵଗୁଡ଼ିକ ସମତଳର ବାହାରେ ପଡ଼େ । ଏ ବସ୍ତୁଗୁଡ଼ିକୁ ତ୍ରି-ମାତ୍ରିକ (Three-Dimentional) ବା 3-D ଆକୃତିବିଶିଷ୍ଟ ବସ୍ତୁ କୁହାଯାଏ । ଉକ୍ତ ବସ୍ତୁଗୁଡ଼ିକୁ ‘ଘନପଦାର୍ଥ’ (Solid)ର ଆଖ୍ୟା ଦିଆଯାଇଥାଏ ।

→ ଦଦୁଫଲକ :

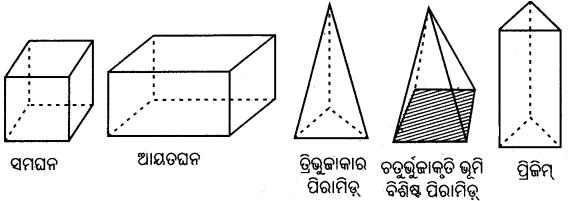
• ବସ୍ତୁଗୁଡ଼ିକର ଗୋଟିଏ ଗୋଟିଏ ପାର୍ଶ୍ଵ (Face) ବୋଲି କହୁ । ଦୁଇଟି ପାର୍ଶ୍ଵ ମିଳିତହୋଇ ଗୋଟିଏ ଗୋଟିଏ ରେଖାଖଣ୍ଡ ସୃଷ୍ଟି କରନ୍ତି । ଉକ୍ତ ରେଖାଖଣ୍ଡଗୁଡ଼ିକ ଘନବସ୍ତୁର ଧାର (Edge) ଅଟନ୍ତି । ପୁନଶ୍ଚ ଦୁଇ ବା ତତୋଽଧୂକ ଧାରଗୁଡ଼ିକ ମିଳିତହୋଇ ଘନପଦାର୍ଥର ଶୀର୍ଷ (Vertex) ସୃଷ୍ଟି କରିଥା’ନ୍ତି । ଏହିପରି ଘନବସ୍ତୁଗୁଡ଼ିକୁ ଗୋଟିଏ ଗୋଟିଏ ବହୁଫଳକ (Polyhedron) କୁହାଯାଏ ।
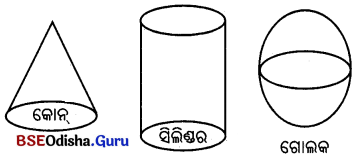
• ଯେଉଁ ଘନବସ୍ତୁଗୁଡ଼ିକର ପାର୍ଶ୍ଵଗୁଡ଼ିକ ଗୋଟିଏ ଗୋଟିଏ ବହୁଭୁଜ, ସେଗୁଡ଼ିକୁ ବହୁଫଳକ କୁହାଯାଏ; କିନ୍ତୁ ଯେଉଁ ଘନବସ୍ତୁଗୁଡ଼ିକର ପାର୍ଶ୍ଵଗୁଡ଼ିକ ବହୁଭୁଜାକାର ନୁହଁନ୍ତି ସେଗୁଡ଼ିକୁ ଅଣ-ବହୁଫଳକ ଘନବସ୍ତୁ କହନ୍ତି । ଉଦାହରଣ (1) କୋନ୍ (2) ସିଲିଣ୍ଡର (3) ଗୋଲକ ।
  

 

• ଯଦି ଏକ ବହୁଫଳକର ପାର୍ଶ୍ଵଗୁଡ଼ିକ ସୁଷମ ବହୁଭୁଜଦ୍ୱାରା ଗଠିତ ହୋଇଥାଏ ଏବଂ ସମାନସଂଖ୍ୟକ ପାର୍ଶ୍ଵ ମିଳିତହୋଇ ଘନବସ୍ତୁଟିର ଶୀର୍ଷ ସୃଷ୍ଟି କରୁଥା’ନ୍ତ; ତେବେ ଉକ୍ତ ବହୁଫଳକକୁ ସୁଷମ ବହୁଫଳକ କୁହାଯାଏ । (1) ସମଘନ, (2) ଟେଟ୍ରାହେନ୍ଦ୍ରନ୍
  ବିଭକ୍ତ କରାଯାଇଛି; ଯଥା – (1) ପ୍ରିଜିମ୍ (2) ପିରାମିଡ଼୍ ।
• ପ୍ରିଜିମ୍ ଏକ ବହୁଫଳକ, ଯାହାର ଭୂମି ଓ ଉପର ପାର୍ଶ୍ଵଦ୍ଵୟ ସର୍ବସମ (ସମକ୍ଷେତ୍ରଫଳବିଶିଷ୍ଟ) ବହୁଭୁଜ ଏବଂ ଅନ୍ୟ ପାର୍ଶ୍ଵଗୁଡ଼ିକ ସାମାନ୍ତରିକକ୍ଷେତ୍ର ବିଶିଷ୍ଟ ।
• ପିରାମିଡ଼ ଏକ ବହୁଫଳକ, ଯାହାର ଭୂମି ଏକ ବହୁଭୁଜ ଏବଂ ପାର୍ଶ୍ଵପୃଷ୍ଠଗୁଡ଼ିକ (Lateral surfaces) ତ୍ରିଭୁଜାକାର ଓ ଏକ ସାଧାରଣ ଶୀର୍ଷ (Vertex) ବିଶିଷ୍ଟ ହୋଇଥାଏ ।
• ଏକ ପ୍ରିଜିମ୍ କିମ୍ବା ଏକ ପିରାମିଡ଼ର ବିଶେଷ ନାମକରଣ ଏହାର ଭୂମିକୁ ଆଧାର କରି ହୋଇଥାଏ ।
• ବି.ଦ୍ର. : (1) ଯେଉଁ ତ୍ରିଭୁଜାକାର ପିରାମିଡ୍‌ର ପ୍ରତ୍ୟେକ ପାର୍ଶ୍ବ ଗୋଟିଏ ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜ, ତାହାକୁ ଟେଟ୍ରାହେନ୍ଦ୍ରନ୍ (Tetrahedron) ହୋଇଥାଏ |
  (2) ଯେଉଁ ବର୍ଗୀକୃତି ପ୍ରିଜିମ୍‌ର ପ୍ରତ୍ୟେକ ପାର୍ଶ୍ବ ଗୋଟିଏ ଗୋଟିଏ ବର୍ଗାକାରକ୍ଷେତ୍ର, ତାହାକୁ ସମଘନ (cube) ହୋଇଥାଏ |

→ ବହୁଫଳକର ଶୀର୍ଷ, ଧାର ଏବଂ ପାର୍ଶ୍ଵ :
ସ୍ଵିସ୍ ଗଣିତଜ୍ଞ ଲିଓନାର୍ଡ଼ ଇଉଲର୍‌ (Leonard Euler, 1707-1783) ଗୋଟିଏ ବହୁଫଳକର ଶୀର୍ଷ (V), ପାର୍ଶ୍ଵ (F), ଏବଂ ଧାର (E) ସଂଖ୍ୟାକୁ ନେଇ ପ୍ରଥମ କରି ସେମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ଏକ ସମ୍ବନ୍ଧକୁ ସୂତ୍ର ଆକାରରେ ପ୍ରଣୟନ କରିଥିଲେ । ସେ ସୂତ୍ରଟି ହେଲା V + F – E = 2 । ଏହାକୁ ଇଉଲରଙ୍କ ସୂତ୍ର କତୃନ୍ତି |

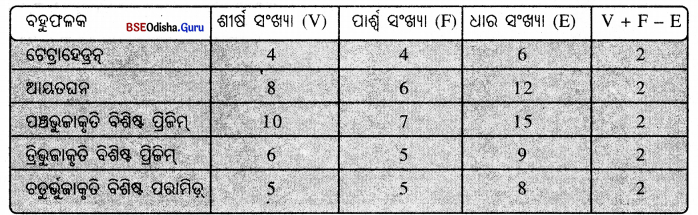
ମନେରଖ :

• ଗୋଟିଏ ପ୍ରିଜିମ୍‌ ଶୀର୍ଷସଂଖ୍ୟା, ଏହାର ଭୂମିର ବାହୁ ସଂଖ୍ୟାର ଦୁଇଗୁଣ ।
• ଗୋଟିଏ ପିରାମିଡ଼ର ଶୀର୍ଷସଂଖ୍ୟା, ଏହାର ଭୂମିର ବାହୁ ସଂଖ୍ୟାରୁ 1 ଅଧିକ ।
• ଗୋଟିଏ ପ୍ରିଜିମ୍‌ର ପାର୍ଶ୍ଵସଂଖ୍ୟା, ଏହାର ଭୂମିର ବାହୁ ସଂଖ୍ୟାଠାରୁ 2 ଅଧିକ ।
• ଗୋଟିଏ ପିରାମିଡ଼ର ପାର୍ଶ୍ଵସଂଖ୍ୟା, ଏହାର ଭୂମିର ବାହୁସଂଖ୍ୟାରୁ l ଅଧିକ ।

→ ଘନବସ୍ତୁ (ବହୁଫଳକ)ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ (Surface Area of a Polyhedron) :

• ଆୟତଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2(ଦୈର୍ଘ୍ୟ x ଉଚ୍ଚତା + ପ୍ରସ୍ଥ × ଉଚ୍ଚତା + ଦୈର୍ଘ୍ୟ x ପ୍ରସ୍ଥ)
• ଆୟତଘନର ପାର୍ଶ୍ଵ ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2 x ଉଚ୍ଚତା (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ)
• ସମଘନର ପାର୍ଶ୍ଵ ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 6(ବାହୁ)²
• ସମଘନର ପାର୍ଶ୍ଵ ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 4(ବାହୁ)²

→ ଘନବସ୍ତୁ (ବହୁଫଳକ)ର ଘନଫଳ :

• କୌଣସି ଘନବସ୍ତୁ ବାୟୁ, ଜଳ ଅଥବା ଶୂନ୍ୟରେ ଅଧ‌ିକାର କରିଥିବା ସ୍ଥାନର ପରିମାପକୁ ଉକ୍ତ ବସ୍ତୁର ଘନଫଳ ବା ଆୟତନ କୁହାଯାଏ ।
• ଆୟତଘନର ଘନଫଳ = ଦୈର୍ଘ୍ୟ × ପ୍ରସ୍ଥ × ଉଚ୍ଚତା = ଭୂମିର କ୍ଷେତ୍ରଫଳ × ଉଚ୍ଚତା
• ସମଘନର ଘନଫଳ = (ବାହୁର ଦୈର୍ଘ୍ୟ)³ ଘନ ଏକକ ।

ଘନଫଳର ଏକକ :
1000 ଘନ ମିଲିମିଟିର = 1 ଘନ ସେ.ମି.
1000 ଘନ ସେ.ମି. = 1 ଘନ ସେ.ମି.
1000 ଘନ ସେ.ମି. = 1 ଘନ ମି.
1000 ଘନ ମି. = 1 ଶନ ବେଳା.ମି.
1000 ଶନ ବେଳା.ମି. = 1 ଘନ ହେକ୍ନୋ.ମି.
1000 ଘନ ହେକ୍ନୋ.ମି. = 1 ଘନ କି.ମି.