Odisha State Board BSE Odisha 8th Class Maths Solutions Algebra Chapter 8 ବ୍ୟାବସାୟିକ ଗଣିତ Ex 8(c) Textbook Exercise Questions and Answers.
BSE Odisha Class 8 Maths Solutions Algebra Chapter 8 ବ୍ୟାବସାୟିକ ଗଣିତ Ex 8(c)
Question 1.
800 ଟଙ୍କାର ୫% ହାରରେ ଦୁଇବର୍ଷର ଚକ୍ରବୃଦ୍ଧି ସୁଧ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ମୂଳଧନ (P) = 800 ଟଙ୍କା, ସୁଧହାର (R) = 8% ଓ ସମୟ (n) = 2 ବର୍ଷ
ସମୂଳ ଚକ୍ରବୃଦ୍ଧି (A) = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{n}}=800\left(1+\frac{8}{100}\right)^2=800\left(1+\frac{2}{25}\right)^2\)
= \(800\left(\frac{27}{25}\right)^2=800 \times \frac{27}{25} \times \frac{27}{25}\) = ଟ. 933.12
ଚକ୍ରବୃଦ୍ଧି ସୁଧ = A – P = 6. 933.12 – 6. 800.00 ଟ. 133.12
∴ ନିର୍ଦେୟ ଚକ୍ରବୃଦ୍ଧି ସୁଧ ଟ.133.12 ।
![]()
Question 2.
1500 ଟଙ୍କାର 7% ହାରରେ ଦୁଇବର୍ଷର ସମୂଳ ଚକ୍ରବୃଦ୍ଧି ନିଶ୍ଚୟ କର ।
ସମାଧାନ :
ମୂଳଧନ (P) = 1500 ଟଙ୍କା, ସୁଧହାର (R) = 7% ଓ ସମୟ (n) = 2 ବର୍ଷ
ସମୂଳ ଚକ୍ରବୃଦ୍ଧି ସୁଧ (A) = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{n}}=1500\left(1+\frac{7}{100}\right)^2=1500\left(1+\frac{107}{100}\right)^2\)
= 1500 × \(\frac{107}{100}\) × \(\frac{107}{100}\) = ଟ. 1717.35
∴ ନିଶ୍ଚେୟ ସମୂଳ ଚକ୍ରବୃଦ୍ଧି ଟ. 1717.35 ।
Question 3.
5000 ଟଙ୍କାର 10% ହାରରେ 3 ବର୍ଷର ଚକ୍ରବୃଦ୍ଧି ସୁଧ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ମୂଳଧନ (P) = 5000 ଟଙ୍କା, ସୁଧହାର (R) = 10% ଓ ସମୟ (n) = 3 ବର୍ଷ
ସମୂଳ ଚକ୍ରବୃଦ୍ଧି ସୁଧ (A) = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{n}}=5000\left(1+\frac{10}{100}\right)^3=5000\left(1+\frac{1}{10}\right)^3\)
= 5000 × \((\frac{107}{100})^3\) = 5000 × \(\frac{11}{10}\) × \(\frac{11}{10}\) × \(\frac{11}{10}\) = 6655 ଟଙ୍କା
ଚକ୍ରବୃଦ୍ଧି ସୁଧ = A – P = (6655 – 5000) ଟଙ୍କା = 1655 ଟଙ୍କା
∴ ନିର୍ଦେୟ ଚକ୍ରବୃଦ୍ଧି ସୁଧ 1655 ଟଙ୍କା ।
![]()
Question 4.
8000 ଟଙ୍କାର 5% ହାରରେ 3 ବର୍ଷର ଚକ୍ରବୃଦ୍ଧି ସୁଧ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ମୂଳଧନ (P) = 8000 ଟଙ୍କା, ସୁଧହାର (R) = 5% ଓ ସମୟ (n) = 3 ବର୍ଷ
ସମୂଳ ଚକ୍ରବୃଦ୍ଧି (A) = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{n}}=8000\left(1+\frac{5}{100}\right)^3=5000\left(1+\frac{1}{20}\right)^3\)
= 8000 × \((\frac{21}{100})^3\) = 8000 × \(\frac{21}{10}\) × \(\frac{21}{10}\) × \(\frac{21}{10}\) = 9261 ଟଙ୍କା
ଚକ୍ରବୃଦ୍ଧି ସୁଧ = A – P = (9261 – 8000) ଟଙ୍କା = 1261 ଟଙ୍କା
∴ ନିଶ୍ଚେୟ ଚକ୍ରବୃଦ୍ଧି ସୁଧ 1261 ଟଙ୍କା ।
Question 5.
ଜଣେ ବ୍ୟକ୍ତି ଏକ ଧାନବୁଣା ଯନ୍ତ୍ର ପାଇଁ 10% ସୁଧ ହାରରେ ବ୍ୟାଙ୍କରୁ 5000 ଟଙ୍କା ଋଣ କଲେ । 3 ବର୍ଷ ପରେ ସେ କେତେ ଟଙ୍କା ଦେଇ ବ୍ୟାଙ୍କରୁ ଋଣମୁକ୍ତ ହେବେ ?
ସମାଧାନ :
ରଣର ପରିମାଣ (P) = 5000 ଟଙ୍କା, ସୁଧହାର (R) = 10% ଓ ସମୟ (n) = 3 ବର୍ଷ
ସମୂଳ ଚକ୍ରବୃଦ୍ଧି (A) = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{n}}=8000\left(1+\frac{10}{100}\right)^3=5000\left(1+\frac{1}{10}\right)^3\)
= 5000 × \((\frac{21}{100})^3\) = 5000 × \(\frac{11}{10}\) × \(\frac{11}{10}\) × \(\frac{11}{10}\) = 6655 ଟଙ୍କା
∴ 3 ବର୍ଷ ପରେ ସେ 6655 ଟଙ୍କା ଦେଇ ବ୍ୟାଙ୍କରୁ ଋଣମୁକ୍ତ ହେବେ ।
Question 6.
କମଳା ଗୋଟିଏ ସ୍କୁଟର କିଣିବାପାଇଁ ବ୍ୟାଙ୍କରୁ 26,400 ଟଙ୍କା 15% ବାର୍ଷିକ ଚକ୍ରବୃଦ୍ଧିରେ ଆଣିଲା । 2 ବର୍ଷ 4 ମାସ ପରେ କେତେ ଟଙ୍କା ବ୍ୟାଙ୍କକୁ ଦେଇ ଋଣମୁକ୍ତ ହେବେ ?
ସମାଧାନ :
ପ୍ରଥମେ କମଳାର ଦୁଇବର୍ଷର ସମୂଳ ଚକ୍ରବୃଦ୍ଧି ନିରୂପଣ କରିବା ।
ଏଠାରେ ଋଣର ପରିମାଣ (P) = 26400 ଟଙ୍କା, ସୁଧହାର (R) = 15%, n = 2 ବର୍ଷ ।
∴ ସମୂଳ ଚକ୍ରବୃଦ୍ଧି (A) = \(P\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{n}}=26400\left(1+\frac{15}{100}\right)^2\)
= 26400 × \(\frac{115}{10}\) × \(\frac{115}{10}\) = 34914 ଟଙ୍କା
4 ମାସର ସରଳ ସୁଧପାଇଁ ମୂଳଧନ (P) = 34914 ଟଙ୍କା,
ସୁଧହାର (R) = 15%, ସମୟ (T) = \(\frac{12}{4}\) ବର୍ଷ = \(\frac{1}{3}\) ବର୍ଷ
∴ ସୁଧ I = \(\frac{\text { PRT }}{100}=\frac{34914 \times 15 \times \frac{1}{3}}{100}=\frac{34914 \times 15 \times 1}{300}\)
ମୋଟ ଦେୟ = 34914 + 1745.70 6 = 36,659.70 ଟଙ୍କା
∴ 2 ବର୍ଷ 4 ମାସ ପରେ କମଳା 36,659.70 ଟଙ୍କା ବ୍ୟାଙ୍କକୁ ଦେଇ ଋଣମୁକ୍ତ ହେବେ ।
![]()
Question 7.
ବାର୍ଷିକ 4% ହାରରେ 6250.00 ଟଙ୍କା କେତେ ବର୍ଷପାଇଁ ବ୍ୟାଙ୍କରେ ଜମା ଦେଲେ 510 ଟଙ୍କା ସୁଧ ମିଳିବ ?
ସମାଧାନ :
ମୂଳଧନ (P) = 6250 ଟଙ୍କା, ଚକ୍ରବୃଦ୍ଧି ସୁଧ = 510 ଟଙ୍କା, ସୁଧହାର (R) = 4%
ସମୂଳ ଚକ୍ରବୃଦ୍ଧି (A) = P + ଚକ୍ରବୃଦ୍ଧି ସୁଧ = (6250 + 510) ଟଙ୍କା = 6760 ଟଙ୍କା
ମନେକର ସମୟ = n ବର୍ଷ । ଆମେ ଜାଣିଛୁ, A = \(P\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{n}}\)
⇒ \(6760=6250\left(1+\frac{4}{100}\right)^{\mathrm{n}} \Rightarrow \frac{6760}{6250}=\left(1+\frac{1}{25}\right)^{\mathrm{n}}\)
⇒ \(\frac{676}{625}=\left(\frac{26}{25}\right)^{\mathrm{n}} \Rightarrow\left(\frac{26}{25}\right)^2=\left(\frac{26}{25}\right)^{\mathrm{n}} \Rightarrow \mathrm{n}=2\)
∴ ବ୍ୟାଙ୍କରେ 6250 ଟଙ୍କା 2 ବର୍ଷ ପାଇଁ ଜମାଦେଲେ 510 ଟଙ୍କା ଚକ୍ରବୃଦ୍ଧି ସୁଧ ମିଳିବ ।
Question 8.
କୌଣସି ମୂଳଧନର 5% ହାରରେ 3 ବର୍ଷର ସରଳସୁଧ 540 ଟଙ୍କା । ସେହି ମୂଳଧନର ସମାନ ସୁଧ ହାରରେ ଓ ସମାନ ସମୟରେ ଚକ୍ରବୃଦ୍ଧି ସୁଧ କେତେ ହେବ ?
ସମାଧାନ :
ଏଠାରେ ସୁଧହାର (R) = 5, ସମୟ (T) = 3 ବର୍ଷ, ସୁଧ (1) = 540 ଟଙ୍କା
ମନେକର ମୂଳଧନ = P ଟଙ୍କା
ମୂଳଧନ (P) = \(\frac{100 I}{RT}\) ଟଙ୍କା = \(\frac{100 × 540}{5×3}\) ଟଙ୍କା = 3600 ଟଙ୍କା
ପୁନଶ୍ଚ ମୂଳଧନ (P) = 3600 ଟଙ୍କା, ସୁଧହାର (R) = 5, ସମୟ (n) = 3
∴ ସମୂଳ ଚକ୍ରବୃଦ୍ଧି ସୁଧ (A) = \(P\left(1+\frac{R}{100}\right)^n\)
= \(3600\left(1+\frac{5}{100}\right)^3=3600 \times \frac{21}{20} \times \frac{21}{20} \times \frac{21}{20}\) ଟଙ୍କା = ଟ. 4167.45
∴ ଚକ୍ରବୃଦ୍ଧି ସୁଧ = ଟ. 4167.45 – ଟ. 3600.00 = ଟ. 567.45
![]()
Question 9.
କୌଣସି ମୂଳଧନର 10% ହାରରେ 3 ବର୍ଷରେ ଚକ୍ରବୃଦ୍ଧି ସୁଧ ଓ ସରଳ ସୁଧର ପାର୍ଥକ୍ୟ ଟ. 93.00 । ମୂଳଧନ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ମନେକର ମୂଳଧନ = P ଟଙ୍କା, ସୁଧର ହାର (R) = 10%, ସମୟ (T) = 3 ବର୍ଷ
∴ ସରଳ ସୁଧ (I) = \(\frac{PRT}{100}=\frac{P×10×3}{100}\) ଟଙ୍କା = \(\frac{3p}{10}\) ଟଙ୍କା
ଚକ୍ରବୃଦ୍ଧି ସୁଧ ପାଇଁ ମୂଳଧନ = P ଟଙ୍କା, ସୁଧର ହାର (R) = 10%, ସମୟ (n) = 3 ବର୍ଷ
∴ ସମୂଳ ଚକ୍ରବୃଦ୍ଧି ସୁଧ (A) = \(P\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{n}}=\mathrm{P}\left(1+\frac{10}{100}\right)^3\)
= \(P\left(1+\frac{1}{10}\right)^3=P\left(\frac{11}{10}\right)^3=\frac{1331 P}{1000}\) ଟଙ୍କା ।
ଚକ୍ରବୃଦ୍ଧି ସୁଧ = A – P = \(\frac{1331 P}{1000}\) – P = 1331 P – 1000 P = 331 P ଟଙ୍କା ।
ପ୍ରଶ୍ବାନୁସାରେ, \(\frac{331 P}{1000}-\frac{3 P}{10}\) = 93 ⇒ \(\frac{331 P-300 P}{1000}\) = 93
⇒ 31P = 93000 ⇒ P = \(\frac{93000}{31}\) = 3000
∴ ନିର୍ମେୟ ମୂଳଧନ 3000 ଟଙ୍କା ।
Question 10.
ସୁଧ 6 ମାସ ଅନ୍ତରରେ ଦେୟ ବାର୍ଷିକ 12.5% ହାରରେ 2560 ଟଙ୍କାର \(1 \frac{1}{2}\) ବର୍ଷର ସମୂଳ ଚକ୍ରବୃଦ୍ଧି ସୁଧ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ଏଠାରେ ମୂଳଧନ (P) = 2560 ଟଙ୍କା, ସୁଧହାର (R) = %
(∵ ବାର୍ଷିକ ସୁଧହାର 12.5% ବା \(12 \frac{1}{2}\)% ହେଲେ, 6 ମାସର ସୁଧ ହାର = 25×1-25%)
ସମୟ (n) = 3 (ପ୍ରତି 6 ମାସ ଏକକ ସମୟ)
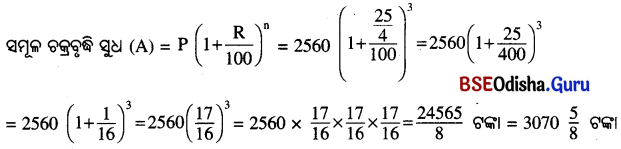
∴ ନିଶ୍ଚେୟ ସମୂଳ ଚକ୍ରବୃଦ୍ଧି ସୁଧ \(3070 \frac{5}{8}\) ଟଙ୍କା ।
![]()
Question 11.
ସୁଧ 6 ମାସ ଅନ୍ତରରେ ଦେୟ ବାର୍ଷିକ 14% ହାରରେ 5000 ଟଙ୍କାର \(1 \frac{1}{2}\) ବର୍ଷର ଚକ୍ରବୃଦ୍ଧି ସୁଧ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ଏଠାରେ ବାର୍ଷିକ ସୁଧର ହାର 14% ହେଲେ 6 ମାସର ସୁଧହାର (R) = \(\frac{14}{2}\)% = 7%
ଏଠାରେ ମୂଳଧନ (P) = 5000 ଟଙ୍କା, ସୁଧହାର (R) = 7%, ସମୟ (n) = 3 (ପ୍ରତି 6 ମାସ ଏକକ ସମୟ)
∴ ସମୂଳ ଚକ୍ରବୃଦ୍ଧି ସୁଧ = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{n}}=5000\left(1+\frac{7}{100}\right)^3\)
= \(5000 \times\left(\frac{107}{100}\right)^3=5000 \times \frac{107 \times 107 \times 107}{100 \times 100 \times 100}\) = ଟ. 6125.22
ଚକ୍ରବୃଦ୍ଧି ସୁଧ = A – P = ଟ. 6125.22 – ଟ. 5000.00 = ଟ. 1125.22
∴ ଚକ୍ରବୃଦ୍ଧି ସୁଧ ଟ. 1125.22 ।
Question 12.
ସୁଧ 4 ମାସ ଅନ୍ତରରେ ଦେୟ ସର୍ଭରେ ଜଣେ ବ୍ୟକ୍ତି ବାର୍ଷିକ 10% ହାରରେ 1 ବର୍ଷର ଚକ୍ରବୃଦ୍ଧି ସୁଧ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ଏଠାରେ ବାର୍ଷିକ ସୁଧର ହାର 10% ହେଲେ, 4 ମାସର ସୁଧହାର = \(\frac{10}{3}\)
ମନେକର ମୂଳଧନ = P ଟଙ୍କା, ସୁଧର ହାର (R) = \(\frac{10}{3}\), ସମୟ 4 ମାସ = \(\frac{12}{4}\) = 3
∴ ସମୂଳ ଚକ୍ରବୃଦ୍ଧି ସୁଧ (A) = \(P\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{n}}=\mathrm{P}\left(1+\frac{10}{300}\right)^3=P\left(1+\frac{1}{30}\right)^3\)
= \(\frac{31}{30} \times \frac{31}{30} \times \frac{31}{30} \mathrm{P}=\frac{29791}{27000}\) P ଟଙ୍କା
ଚକ୍ରବୃଦ୍ଧି ସୁଧ = A – P = \(\frac{29791}{27000}\) P – P = \(\frac{29791-27000}{27000}\) P ଟଙ୍କା = \(\frac{2791}{27000}\) P ଟଙ୍କା ।
![]()
Question 13.
ଗୋଟିଏ ଘରର ମୂଲ୍ୟ 2,00,000 ଟଙ୍କା । ପ୍ରତିବର୍ଷ ଏହାର ମୂଲ୍ୟ % ହାରରେ ହ୍ରାସପାଏ; ତେବେ 3 ବର୍ଷ ପରେ ଏହାର ହ୍ରାସପ୍ରାପ୍ତ ମୂଲ୍ୟ କେତେ ହେବ ?
ସମାଧାନ :
ପ୍ରାରମ୍ଭିକ ମୂଲ୍ୟ (P) = 200000 ଟଙ୍କା, ହାର (R) = 6%, ସମୟ (n) = 3 ବର୍ଷ
3 ବର୍ଷ ପରବର୍ତ୍ତୀ ମୂଲ୍ୟ (A) = \(\mathrm{P}\left(1-\frac{\mathrm{R}}{100}\right)^{n}=200000\left(1-\frac{6}{100}\right)^3=200000\left(1-\frac{3}{50}\right)^3\)
= \(200000\left(\frac{47}{50}\right)^3=200000 \times \frac{47}{50} \times \frac{47}{50} \times \frac{47}{50}\) = ଟ. 166116.80
∴ 3 ବର୍ଷ ପରେ ଘରର ହ୍ରାସପ୍ରାପ୍ତ ମୂଲ୍ୟ ଟ.166116.80 ହେବ ।
Question 14.
ଗୋଟିଏ ଗ୍ରାମର ଲୋକସଂଖ୍ୟା 20,000 । ପ୍ରତିବର୍ଷ ଏହାର ଲୋକ ସଂଖ୍ୟା 7% ବୃଦ୍ଧି ପାଇଲେ ଦୁଇ- ବର୍ଷପରେ ଲୋକସଂଖ୍ୟା କେତେ ହେବ ?
ସମାଧାନ :
ଏଠାରେ ପ୍ରାରମ୍ଭିକ ମୂଲ୍ୟ (P) = 20,000, ବାର୍ଷିକ ବୃଦ୍ଧି ହାର (R) = 7%, ସମୟ (n) = 2 ବର୍ଷ
2 ବର୍ଷ ପରେ ବୃଦ୍ଧିପ୍ରାପ୍ତ ଲୋକସଂଖ୍ୟା (A) = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{n}=20000\left(1+\frac{7}{100}\right)^2=20000\left(\frac{107}{100}\right)^2\)
= \(20000 \times \frac{107}{100} \times \frac{107}{100}=22898\)
∴ 2 ବର୍ଷ ପରେ ଉକ୍ତ ଗ୍ରାମର ଲୋକସଂଖ୍ୟା 22898 ।
![]()
Question 15.
ଗୋଟିଏ ମଟର ସାଇକେଲର କ୍ରୟମୂଲ୍ୟ ଟ.42,000 । ପ୍ରତିବର୍ଷ ପରେ ଏହାର ମୂଲ୍ୟ 8% ହାରରେ ହ୍ରାସ – ପାଏ; ତେବେ 2 ବର୍ଷ ପରେ ମଟର ସାଇକେଲ ମୂଲ୍ୟ କେତେ ହେବ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ଏଠାରେ ପ୍ରାରମ୍ଭିକ ମୂଲ୍ୟ (P) = 42000 ଟଙ୍କା, ହାର (R) = 8%, ସମୟ (n) = 2 ବର୍ଷ
∴ ଦୁଇବର୍ଷ ପରେ ଏହାର ଦାମ୍ (A) = \(P\left(1-\frac{R}{100}\right)^n=42000\left(1-\frac{8}{100}\right)^2\) ଟଙ୍କା
= \(42000 \times \frac{92}{100} \times \frac{92}{100}\) ଟଙ୍କା = 35548.80 ଟଙ୍କା ।
∴ 2 ବର୍ଷ ପରେ ମଟର ସାଇକେଲର ମୂଲ୍ୟ ଟ. 35548.80 ହେବ ।
