BSE Odisha 8th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(a)

Odisha State Board BSE Odisha 8th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(a)

Question 1.
କେତେକ ସମକୋଣୀ ତ୍ରିଭୁଜର ସମକୋଣସଂଲଗ୍ନ ବାହୁ ଦୁଇଟିର ଦୈର୍ଘ୍ୟ ନିମ୍ନରେ ଦିଆଯାଇଛି । ପିଥାଗୋରୀୟ ତ୍ରୟୀ ସାହାଯ୍ୟରେ ପ୍ରତ୍ୟେକ ସମକୋଣୀ ତ୍ରିଭୁଜର କର୍ପୂର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
(i) 3 ମି. ଓ 4 ମି.
(ii) 5 ସେ.ମି. ଓ 12 ସେ.ମି.
(iii) 7 ସେ.ମି. ଓ 24 ସେ.ମି.
(iv) 8 ମି. ଓ 15 ମି.
(v) 1.5 ସେ.ମି. ଓ 2 ସେ.ମି.
(vi) 10 ସେ.ମି. ଓ 24 ସେ.ମି.
Solution:
(i) 5 ମି. ( ∵3, 4 ଓ 5 ଗଣନ ସଂଖ୍ୟାତ୍ରୟ ପିଥାଗୋରୀୟ ଟ୍ରିପ୍‌ଲ)
(ii) 13 ସେ.ମି. (∵ 15, 12 ଓ 13 ଗଣନ ସଂଖ୍ୟାତ୍ରୟ ପିଥାଗୋରୀୟ ଟ୍ରିପ୍‌ଲ)
(iii) 25 ସେ.ମି. (∵ 7, 24 ଓ 25 ଗଣନ ସଂଖ୍ୟାତ୍ରୟ ପିଥାଗୋରୀୟ ଟ୍ରିପ୍‌ଲ)
(iv) 17 ମି. (∵ 8, 15 ଓ 17 ଗଣନ ସଂଖ୍ୟାତ୍ରୟ ପିଥାଗୋରୀୟ ଟ୍ରିପ୍‌ଲ)
(v) 2.5 ସେ.ମି. (∵1.5, 2 ଓ 2.5 ପରିମେୟ ସଂଖ୍ୟାତ୍ରୟ ପିଥାଗୋରୀୟ ଟ୍ରିପ୍‌ଲ)
(vi) 26 ସେ.ମି. (∵ 3, 4 ଓ 5 ଗଣନ ସଂଖ୍ୟାତ୍ରୟ ପିଥାଗୋରୀୟ ଟ୍ରିପ୍‌ଲ)

Question 2.
ନିମ୍ନରେ ସମକୋଣୀ ତ୍ରିଭୁଜର ଯଥାକ୍ରମେ କର୍ପୂର ଦୈର୍ଘ୍ୟ ଓ ଏକ ବାହୁର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଅଛି । ତ୍ରିଭୁଜର ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ ସ୍ଥିର କର ।
(i) 2.5 ସେ.ମି. ଓ 2.4 ସେ.ମି.
(ii) 4.1 ମି. ଓ 4 ମି.
(iii) 12.5 ମି. ଓ 10 ମି.
(iv) 125 ମି. ଓ 100 ମି.
(v) 299 ମି. ଓ 276 ମି..
Solution:
(i) ବାହୁର ଦୈର୍ଘ୍ୟ = 2.5 ସେ.ମି. ଓ ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ = 2.4 ସେ.ମି.
∴ ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ = \(\sqrt{(2 \cdot 5)^2-(2 \cdot 4)^2}\) = \(\sqrt{6 \cdot 25-5 \cdot 76}\) = \(\sqrt{0 \cdot 49}\) = 0.7 ସେ.ମି.
ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ ନିଣ୍ଡୟର ବିକନ୍ତ ପଣାଲା :
\(\sqrt{(2 \cdot 5)^2-(2 \cdot 4)^2}\) = \(\sqrt{(2 \cdot 5+2 \cdot 4)(2 \cdot 5-2 \cdot 4)}\) [∵a² – b² = (a + b) (a – b)]
= \(\sqrt{4 \cdot 9 \times 0 \cdot 1}\) = \(\sqrt{0.49}\) = 0.7 ସେ.ମି.

(ii) ବାହୁର ଦୈର୍ଘ୍ୟ = 4.1 ମି. ଓ ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ = 4 ମି.
∴ ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ = \(\sqrt{(4 \cdot 1)^2-(4)^2}\) = \(\sqrt{16 \cdot 81-16}\) = \(\sqrt{0 \cdot 81}\) = 0.9 ମି.

(iii) ବାହୁର ଦୈର୍ଘ୍ୟ = 12.5 ମି. ଓ ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ = 10 ମି.
∴ ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ = \(\sqrt{(12.5)^2-(10)^2}\) = \(\sqrt{(156.25-100)}\) = \(\sqrt{56.25}\) = 7.5 ମି.

(iv) ବାହୁର ଦୈର୍ଘ୍ୟ = 125 ମି. ଓ ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ = 100 ମି.
∴ ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ = \(\sqrt{(125)^2-(100)^2}\) = \(\sqrt{(125+100)(125-100)}\) = \(\sqrt{225 \times 25}\) = 15 × 5 = 75 ମି.
ଅଥବା \(\sqrt{125^2-100^2}\) = \(\sqrt{25^2 \times 5^2-25^2 \times 4^2}\) = \(\sqrt{25^2\left(5^2-4^2\right)}\) = \(\sqrt{25^2 \times 3^2}\) = 25 × 3 = 75 ମି.

(v) ବାହୁର ଦୈର୍ଘ୍ୟ = 299 ମି. ଓ ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ = 276 ସେ.ମି.
∴ ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ = \(\sqrt{(299)^2-(276)^2}\) = \(\sqrt{(299+276)(299-276)}\) = \(\sqrt{575 \times 23}\) = \(\sqrt{5 \times 5 \times 23 \times 23}\) = 5 × 23 = 115 ମି.

Question 3.
ନିମ୍ନରେ କେତେଗୁଡ଼ିଏ ତ୍ରିଭୁଜର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଅଛି । ପ୍ରମାଣ କର ଯେ ପ୍ରତ୍ୟେକ ଗୋଟିଏ ଲେଖାଏଁ ସମକୋଣା ତୁରୁକ |
(i) 11 ସେ.ମି., 60 ସେ.ମି. ଓ 61 ସେ.ମି.
(ii) 0.8 ମି., 1.5 ମି. ଓ 1.7 ମି.
(iii) 0.9 ତେ.ମି., 4 ତେ.ମି. ଓ 4.1 ତେ.ମି.
(iv) 0.7 ସେ.ମି., 24 ସେ.ମି. ଓ 2.5 ସେ.ମି.
Solution:
(i) 11² + 60² = 121 + 3600 = 3721 = (61)²
∴ ଏହା ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜ ।
(ii)
(0.8)² + (1.5)² = 0.64 + 2.25 = 2.89 = (1.7)²
∴ ଏହା ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜ ।

(iii) (0.9)² + (4)² = 0.81 + 16 = 16.81 = (4.1)²
∴ ଏହା ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜ ।

(iv) (0.7)² + (2.4)² = 0.49 + 5.76 = 6.25 = (2.5)²
∴ ଏହା ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜ ।

Question 4.
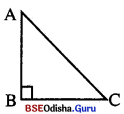
ABC ତ୍ରିଭୁଜରେ ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ ଦିଆଯାଇଛି । ପ୍ରଥମେ ପରୀକ୍ଷା କରି ଦେଖ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ କି ? ଯଦି ଉତ୍ତର ହଁ ହୁଏ, ତେବେ ତ୍ରିଭୁଜର କେଉଁ କୋଣର ପରିମାଣ 90° ହେବ ?
(i) AB = 3 ସେ.ମି., BC = 4 ସେ.ମି. ଏବଂ CA = 5 ସେ.ମି.
(ii) CA = 5 ସେ.ମି., AB = 12 ସେ.ମି. ଏବଂ BC = 13 ସେ.ମି.
(iii) BC = 7 ସେ.ମି., CA = 24 ସେ.ମି. ଏବଂ AB = 25 ସେ.ମି.
(iv) BC = 9 ସେ.ମି., AB = 40 ସେ.ମି. ଏବଂ AC = 41 ସେ.ମି.
(v) AB = 8 ସେ.ମି., BC = 15 ସେ.ମି. ଏବଂ CA = 17 ସେ.ମି.
Solution:
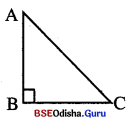
(i) ABC ତ୍ରିଭୁଜରେ AB = 3 ସେ.ମି., BC = 4 ସେ.ମି. ଓ AC = 5 ସେ.ମି. |
(ii) AB² + BC² = (3)² + (4)² = 9 + 16 = 25 = (5)² = AC²
ତେଣୁ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ।
ଏହି ତ୍ରିଭୁଜର ବୃହତ୍ତମ ବାହୁ AC = ତ୍ରିଭୁଜର କଣ୍ଠ ।
AC କର୍ପୂର ସମ୍ମୁଖୀନ କୋଣ ∠ABC ର ପରିମାଣ 90° ହେବ ।

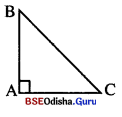
(ii) ABC ତ୍ରିଭୁଜରେ CA = 5 ସେ.ମି., AB = 12 ସେ.ମି. ଏବଂ BC = 13 ସେ.ମି. |
AC² + AB² = 5² + 12² = 25 + 144 = 169 = 13² = BC²
ତେଣୁ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ।
ଏହି ତ୍ରିଭୁଜର ବୃହତ୍ତମ ବାହୁ BC = ତ୍ରିଭୁଜର କର୍ଣ୍ଣ ।
BC କର୍ପୂର ସମ୍ମୁଖୀନ କୋଣ ∠BAC ର ପରିମାଣ 90° ହେବ ।

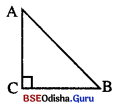
(iii) ABC ତ୍ରିଭୁଜରେ BC = 7 ସେ.ମି., CA = 24 ସେ.ମି. ଏବଂ AB = 25 ସେ.ମି.
BC² + AC² = 7² + 24² = 49 + 576 = 625 = 25² = AB²
ତେଣୁ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ।
ଏହି ତ୍ରିଭୁଜର ବୃହତ୍ତମ ବାହୁ AB = ତ୍ରିଭୁଜର କର୍ଣ୍ଣ ।
AB କର୍ପୂର ସମ୍ମୁଖୀନ କୋଣ ZACB ର ପରିମାଣ 90° ହେବ ।

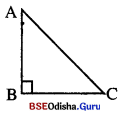
(iv) ABC ତ୍ରିଭୁଜରେ BC = 9 ସେ.ମି., AB = 40 ସେ.ମି. ଏବଂ AC = 41 ସେ.ମି.
BC² + AB² = 9² + 40² = 81 + 1600 = 1681 = 41² = AC²
ତେଣୁ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ।
ଏହି ତ୍ରିଭୁଜର ବୃହତ୍ତମ ବାହୁ AC = ତ୍ରିଭୁଜର କର୍ଣ୍ଣ ।
AC କର୍ପୂର ସମ୍ମୁଖୀନ କୋଣ ∠ABC ର ପରିମାଣ 90° ହେବ ।

(v) ABC ତ୍ରିଭୁଜରେ AB = 8 ସେ.ମି., BC = 15 ସେ.ମି. ଏବଂ CA = 17 ସେ.ମି.
AB² + BC² = 8² + 15² = 64 + 225 = 289 = 17² = AC²
ତେଣୁ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ।
ଏହି ତ୍ରିଭୁଜର ବୃହତ୍ତମ ବାହୁ AC = ତ୍ରିଭୁଜର କଣ୍ଠି ।
AC କର୍ପୂର ସମ୍ମୁଖୀନ କୋଣ ∠ABC ର ପରିମାଣ 90° ହେବ ।

Question 5.
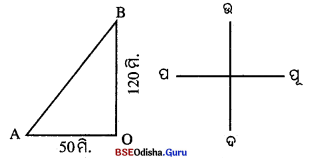
ଜଣେ ବ୍ୟକ୍ତି A ସ୍ଥାନରୁ ବାହାରି ପୂର୍ବ ଦିଗକୁ 50 ମିଟର ଗତିକଲା ପରେ ସେଠାରୁ ଉଭର 120 ମିଟର ଗତିକରି B ନାମକ ସ୍ଥାନରେ ପହଞ୍ଚିଲେ । A ଠାରୁ B ର ଦୂରତା କେତେ ?
Solution:
ଜଣେ ବାହାରି ଗତିପଥ A ରୁ ପୂର୍ବକୁ 50 ମି. ଗତିକରି ‘O’ ବିନ୍ଦୁରେ ପହଞ୍ଚିଲା । ପୁନଶ୍ଚ O ରୁ ଉତ୍ତରକୁ 120 ମି. ଗତିକରି B ନାମକ ସ୍ଥାନରେ ପହଞ୍ଚି AOB ସମକୋଣୀ ତ୍ରିଭୁଜ ଉତ୍ପନ୍ନ ହେଲା ।
ଏହାର m∠O = 90°
∴ AOB ସମକୋଣୀ ତ୍ରିଭୁଜର ସମକୋଣସଂଲଗ୍ନ ବାହୁଦ୍ୱୟ BO = 120 ମି. ଏବଂ AO = 50 ମି. |
A ଓ B ମତରେ ଦୁଇତା = କଣ୍ଡ = AB = \(\sqrt{\mathrm{OB}^2+\mathrm{OA}^2}\) = \(\sqrt{(120)^2+(50)^2}\) (ପିଥାଗୋରୀୟ ଉପପାଦ୍ୟ)
= \(\sqrt{14400+2500}\) = \(\sqrt{16,900}\) = 130 ମିଟର |

Question 6.
20 ମିଟର ଉଚ୍ଚ. ଗୋଟିଏ ତାଳଗଛ ଝଡ଼ରେ ନଇଁ ପଡ଼ିବାରୁ‘ତା’ର ଅଗ୍ରଭାଗ ସେହି ଗଛର ମୂଳଠାରୁ 12 ମିଟର ଦୂରରେ ଅବସ୍ଥିତ ଏକ ସ୍ତମ୍ଭର ଅଗ୍ରଭାଗକୁ ସ୍ପର୍ଶକଲା । ସ୍ତମ୍ଭଟିର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
AB = ତାଳଗଛର ଉଚ୍ଚତା = 20 ମିଟର,
ତାଳଗଛ ଝଡ଼ରେ ନଇଁପଡ଼ିବାରୁ ତା’ର ଅଗ୍ରଭାଗ ସ୍ତମ୍ଭଠାରୁ 12 ମି. ଦୂରରେ ଥ‌ିବା
ସ୍ତମ୍ଭ DCର ଅଗ୍ରଭାଗ C କୁ ସ୍ପର୍ଶକଲା ।

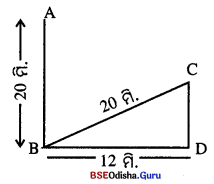
ବର୍ତ୍ତମାନ BDC ସମକୋଣୀ ତ୍ରିଭୁଜର ∠D ସମକୋଣ
AB = BC = 20 ମିଟର, BD = 12 ମିଟର
ପିଥାଗୋରସ୍‌ଙ୍କ ଉପପାଦ୍ୟ ଅନୁସାରେ CD = \(\sqrt{\mathrm{BC}^2-\mathrm{BD}^2}\) = \(\sqrt{20^2-12^2}\) = \(\sqrt{400-144}\) = \(\sqrt{256}\) = 16 ମିଟର
∴ସ୍ତମ୍ଭର ଉଚ୍ଚତା 16 ମିଟର ।

Question 7.
ଗୋଟିଏ କୋଠାଘରର ବାହାର କାନ୍ଥର ପାଦଦେଶରୁ 8 ମିଟର ଦୂରରେ ଗୋଟିଏ ନିଶୁଣି ରଖ୍ କାନ୍ଥକୁ ଡେରିଦେଲେ, ନିଶୁଣିର ଅଗ୍ରଭାଗ କାନ୍ଥର ଉପରକୁ ସ୍ପର୍ଶ କରେ । ନିଶୁଣଟିର ଦୈର୍ଘ୍ୟ 10 ମିଟର ହେଲେ, କାନ୍ଥର ଉଚ୍ଚତା ସ୍ଥିର କର ।
Solution:
କୋଠାର ବାହାର କାନ୍ତର ଇଳତା = AB
ଏହାର ବାହାର ପାଦଦେଶ ‘B’ ଠାରୁ 8 ମି. ଦୂର ‘C’ ଠାରେ ଏକ ନିଶୁଣି
କାନ୍ଥର ଅଗ୍ରଭାଗ ‘A’ ଠାରେ ସ୍ପର୍ଶ କରେ ।

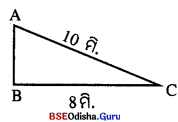
ବର୍ତ୍ତମାନ ABC ସମକୋଣୀ △ର ∠B ସମକୋଣ ।
ନିଶୁଣିର ଦୈର୍ଘ୍ୟ AC = 10 ମିଟର, BC = 8 ମି.
∴ AB = \(\sqrt{\mathrm{AC}^2-\mathrm{BC}^2}\) = \(\sqrt{10^2-8^2}\) = \(\sqrt{100-64}\) = \(\sqrt{36}\) = 6 ମିଟର
∴ କାନ୍ଥର ଉଚ୍ଚତା 6 ମିଟର ।

Question 8.
ଗୋଟିଏ ଘରର ଦୁଇ ବିପରୀତ କାନ୍ଥର ଉଚ୍ଚତା ଯଥାକ୍ରମେ 25 ଡେସି ମି. ଓ 4 ଡେସି ମି. । କାନ୍ଥ ଦୁଇଟିର ଉପରିଭାଗକୁ ଲାଗିଥିବା ଗୋଟିଏ ସଳଖ କଡ଼ିର ଦୈର୍ଘ୍ୟ 65 ଡେସି ମି. ହେଲେ, ଘରର ପ୍ରସ୍ଥ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ଘରର ଦୁଇ ବିପରୀତ କାନ୍ଥ AB ଓ CD | ଘରର ପ୍ରସ୍ଥ : = BC
କଡ଼ିର ଦୈର୍ଘ୍ୟ AD = 65 ଡେସି ମି. AB = 64 ଡେସି ମି. ଏବଂ CD = 25 ତେ.ମି.ମି.
D ବିନ୍ଦୁରୁ AB ଉପରେ ଅଙ୍କିତ ଲମ୍ବର ପାଦବିନ୍ଦୁ M ହେଲେ,
△AMD ରେ MD = BC ଏବଂ

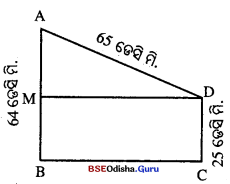
AM = AB – BM = AB – CD = 64 – 25 = 39 ତେ.ମି.ମି.
MD = \(\sqrt{\mathrm{AD}^2-A M^2}\) = \(\sqrt{65^2-39^2}\) = \(\sqrt{4225-1521}\) = \(\sqrt{2704}\) = 52 ତେ.ମି.ମି.
କିନ୍ତୁ MD = BC
∴ ଘରର ପ୍ରସ୍ଥ = BC = 52 ତେ.ମି.ମି.

Question 9.
ଗୋଟିଏ ପୋଖରୀରେ ଥିବା ଏକ ପଦ୍ମକଢ଼ିର ଅଗ୍ରଭାଗ ଜଳ ଉପରକୁ 1 ମିଟର ଦେଖାଯାଉଥିଲା । କିନ୍ତୁ ବାୟୁଦ୍ଵାରା ଏହି କଢ଼ିଟି ଆସ୍ତେ ଆସ୍ତେ ଘୁଞ୍ଚିଯାଇ ମିଟର ଦୂରରେ ଜଳସ୍ତର ସଙ୍ଗେ ମିଶିଗଲା । ପୋଖରୀରେ ଜଳର ଗଭୀରତା ନିଶ୍ଚୟ କର ।
Solution:
AB = ପଦ୍ମନାଡ଼ର ପ୍ରଥମ ଅବସ୍ଥା । ଏହାର AC ଅଂଶ ପାଣି ଉପରକୁ ଦେଖାଯାଉଛି ।
BC = ଜଳର ଗଭୀରତା । ପବନଦ୍ଵାରା ଚାଳିତ ହୋଇ ପଦ୍ମନାଡ଼ଟି 3 ମିଟର ଦୂରରେ D ବିନ୍ଦୁରେ ଜଳ ସହିତ ମିଶିଗଲା ।
BD = ପଦ୍ମନାଡ଼ର ଦ୍ଵିତୀୟ ଅବସ୍ଥା ।
∴ AB = BD = BC + AC
ମନେକର ଜଳର ଗଭୀରତା BC = x ମିଟର
∴ BD = (x + 1) ମିଟର

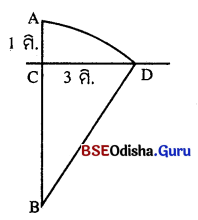
ବରମାନ BCD ସମକୋଣା ପ୍ରତିଭୁଲରହି BD² = BC² + CD²
⇒ (x + 1)² = x² + 3² ⇒ x² + 2x + 1 = x² + 9
⇒ 2x = 9 – 1 ⇒ 2x = 8 ⇒ x = \(\frac { 8 }{ 2 }\) = 4 ମିଟର |
∴ ଜଳର ଗଭୀରତା 4 ମିଟର ।

Question 10.
ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 32 ସେ.ମି. । ତାହାର କର୍ପୂର ଦୈର୍ଘ୍ୟ ଅନ୍ୟ ବାହୁର ଦୈର୍ଘ୍ୟ ଅପେକ୍ଷା ୫ ସେ.ମି. ବୃହତ୍ତର ହେଲେ, କର୍ପୂର ଦୈର୍ଘ୍ୟ ସ୍ଥିର କର ।
Solution:
ABC ସମକୋଣୀ ତ୍ରିଭୁଜର AB ବାହୁର ଦୈର୍ଘ୍ୟ = 32 ସେ.ମି.
ମନେକର BC ବାହୁର ଦୈର୍ଘ୍ୟ = x ସେ.ମି.
ପ୍ରଶାନୁସାରେ AC କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = (x + 8) ସେ.ମି.

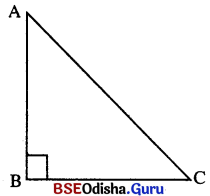
ଆମେ ଜାଣିଛେ, ABC ସମକୋଣୀ ତ୍ରିଭୁଜରେ, AC² = AB² + BC²
⇒ (x + 8)² = (32)² + x² ⇒ x² +8² + 2·x·8 = 1024 + x²
⇒ 64 + 16x = 1024 ⇒ 16x = 1024 – 64
⇒ 16x = 960 ⇒ x = \(\frac { 960 }{ 16 }\) = 60 ⇒ AC = (x + 8) ସେ.ମି.
= (60 + 8) ସେ.ମି. = 68 ସେ.ମି.
∴କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 68 ସେ.ମି. |