BSE Odisha 8th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(c)

Odisha State Board BSE Odisha 8th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(c) Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(c)

Question 1.
ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ 900 ବର୍ଗମିଟର ହେଲେ, ଏହାର ପରିସୀମା ନିର୍ଣ୍ଣୟ କର ।
Solution:
ମନେକର ବର୍ଗାକାରକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ a ମିଟର ।
∴ ବର୍ଗାକାରକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = a² ବର୍ଗମିଟର ।
ପ୍ରଶ୍ନନୁସାରେ, a² = 900 ⇒ a= √900 = 30 ମି.
∴ ବର୍ଗକ୍ଷେତ୍ରର ପରିସୀମା = 4 × a = 4 × 30 = 120 ମିଟର ।

Question 2.
ଗୋଟିଏ ଆୟତାକାର ଘାସପଡ଼ିଆର ଦୈର୍ଘ୍ୟ, ଏହାର ପ୍ରସ୍ଥର ଦୁଇଗୁଣ । ଏହାର କ୍ଷେତ୍ରଫଳ 800 ବର୍ଗମିଟର ହେଲେ, ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ମନେକର ଆୟତକ୍ଷେତ୍ରର ପ୍ରସ୍ଥ = x ମି.
∴ ଦୈର୍ଘ୍ୟ 2x ମି.
ପ୍ରଶ୍ନନୁସାରେ, ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 800 ବ.ମି.
⇒ ଦୈର୍ଘ୍ୟ × ପ୍ରସ୍ଥ = 800 ବ.ମି. (∵ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଦୈର୍ଘ୍ୟ × ପ୍ରସ୍ଥ)
⇒ 2x × x = 800
→ x2 = 400 = x = 20 ମି.
ପ୍ରସ୍ଥ = x = 20 ଏବଂ ଦୈର୍ଘ୍ୟ = 2x = 2 × 20 = 40 ମିଟର ।
∴ ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ 40 ମିଟର ଓ ପ୍ରସ୍ଥ 20 ମିଟର ।

Question 3.
ଗୋଟିଏ ବର୍ଗାକାରକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ 139876 ବର୍ଗମିଟର । ଏହାର ଚାରିପାଖରେ ବାଡ଼ଦେବାରେ ପ୍ରତି ମିଟରକୁ ଟ. 15.00 ହିସାବରେ କେତେ ଖର୍ଚ୍ଚ ହେବ ?
Solution:
ବର୍ଗାକାରକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 139876 ବ.ମି.
∴ ବର୍ଗାକାରକ୍ଷେତ୍ରର ବାହୁ = \(\sqrt{139876}\) = 374 ମି.
∴ ବର୍ଗକ୍ଷେତ୍ରର ପରିସୀମା = 4 × ବାହୁ = 4 × 374 = 1496 ମିଟର ।
ପ୍ରତି ମିଟରକୁ ବାଡ଼ଦେବା ଖର୍ଚ୍ଚ 15 ଟଙ୍କା ହେଲେ,
ବର୍ଗାକାରକ୍ଷେତ୍ରଟିର ଚାରିପାଖରେ ବାଡ଼ଦେବା ଖର୍ଚ୍ଚ
= 1496 × 15 = 22,440 ଖର୍ଚ୍ଚ |
∴ ବର୍ଗାକାରକ୍ଷେତ୍ରର ଚାରିପାଖରେ ବାଡ଼ଦେବାରେ 22440 ଟଙ୍କା ଖର୍ଚ୍ଚ ହେବ ।

Question 4.
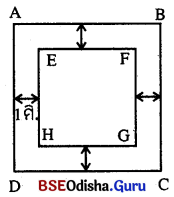
ଗୋଟିଏ ବର୍ଗାକାର ବଗିଚାର ଦୈର୍ଘ୍ୟ 30 ମିଟର । ତାହାର ଭିତର ସୀମାର ଚାରିଧାରକୁ ଲାଗି 1 ମିଟର ଚଉଡ଼ାର ଏକ ରାସ୍ତା ନିର୍ମାଣ କରାଯାଇଛି ।
(i) ରାସ୍ତାର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
(ii) ରାସ୍ତାଟି ତିଆରିପାଇଁ ବର୍ଗମିଟରକୁ ଟ. 240 ପଇସା ହିସାବରେ କେତେ ଖର୍ଚ୍ଚ ହେବ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ABCD ବର୍ଗାକାର ବଗିଚାର ବାହୁର ଦୈର୍ଘ୍ୟ = AB = 30 ମି.
EFGH ବର୍ଗାକାରକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = 30 – (1 × 2) = 28 ମି.
(i) ରାସ୍ତାର କ୍ଷେତ୍ରଫଳ = ABCD ବର୍ଗାକାରକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ – EFGH ବର୍ଗାକାରକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ
= (30)² – (28)² = (30 + 28) (30 – 28)
= 58 × 2 = 116 ଚଟା.ମି.

(ii) 1 ବର୍ଗମିଟରକୁ ଟ. 2.40 ପଇସା ହିସାବରେ
116 ବର୍ଗମିଟରକୁ ଖର୍ଚ୍ଚ ହେବ
= (116 × 2. 40) ଖର୍ଚ୍ଚ = 278.40 ଖର୍ଚ୍ଚ
∴ ରାସ୍ତାଟି ତିଆରି ପାଇଁ 278.40 ଟଙ୍କା ଖର୍ଚ୍ଚ ହେଲା ।

Question 5.
5 ମି. × 3 ମି. ପାପର ଘର ମାଣକୁ ଗାଲିଲ କିଛିଳତାକୁ ଦେଲେ, 60 ସେ.ମି. × 50 ସେ.ମି. ପାପର କେତେ ଖଣ୍ଡ ଟାଇଲ ଆବଶ୍ୟକ ହେବ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ଘର ଚଟାଣର କ୍ଷେତ୍ରଫଳ = 5 ମି. × 3 ମି.
= (5 × 100) ସେ.ମି. × (3 × 100) ସେ.ମି. = 150000 ବଶ ସେ.ମି.
ଗୋଟିଏ ଗାଲଲଭ ଯେତ୍ରପଲ = 60 ସେ.ମି. × 50 ସେ.ମି. = 3000 ବଶ ସେ.ମି.
ଟାଇଲର ସଂଖ୍ୟା = \(\frac { ଘର ଚଟାଣର କ୍ଷେତ୍ରଫଳ }{ ଗାଲିଲ କିଛିଳତାକୁ }\) = \(\frac { 150000 }{ 3000 }\) = 50 ଖର୍ଚ୍ଚ
∴ 50 ଖଣ୍ଡ ଟାଇଲ ଆବଶ୍ୟକ ହେବ |

Question 6.
ରାମ କିଣିଥିବା ଖଣ୍ଡିଏ ଜମିର ଆକାର 20 ମି. × 24 ମି. । ଶ୍ୟାମ କିଣିଥିବା ଖଣ୍ଡିଏ ଜମିର ଆକାର 22 ମି. × 22 ମି. । ଏହି ଦୁଇଖଣ୍ଡ ଜମିର (i) ପରିସୀମାର ଅନ୍ତର (ii) କ୍ଷେତ୍ରଫଳର ଅନ୍ତର ନିର୍ଣ୍ଣୟ କର ।
Solution:
ରାମ କିଣିଥିବା ଜମିର ଦୈର୍ଘ୍ୟ ଏବଂ ପ୍ରସ୍ଥ ଯଥାକ୍ରମେ 24 ମି. 20 ମି. ।
∴ପରିସୀମା = 2 (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ) = 2(24 + 20) = 88 ମିଟର
ଏବଂ କ୍ଷେତ୍ରଫଳ = ଦୈର୍ଘ୍ୟ × ପ୍ରସ୍ଥ = 24 × 20 = 480 ବଗମିଟର |
ଶ୍ୟାମ କିଣିଥିବା କାମିର ଦୈର୍ଘ୍ୟ = 22 ମି. ଏବଂ ପ୍ରସ୍ଥ = 22 ମି. | ଅର୍ଥାତ୍ ଜମିଟି ବର୍ଗାକାରକ୍ଷେତ୍ର ।
∴କ୍ଷେତ୍ରଟିର ପରିସୀମା = 4 × ବାହୁର ଦୈର୍ଘ୍ୟ = 4 × 22 = 88 ମିଟର |
କ୍ଷେତ୍ରଟିର କ୍ଷେତ୍ରଫଳ = (ବାହୁର ଦୈର୍ଘ୍ୟ)² = (22)² = 484 ବର୍ଗମିଟର ।
∴ ରାମ ଓ ଶ୍ୟାମ କିଣିଥିବା ଜମିର ପରିସୀମା ସମାନ ଅର୍ଥାତ୍ ଅନ୍ତର 0।
ଜମିର କ୍ଷେତ୍ରଫଳର ଅନ୍ତର = 484 – 480 = 4 ଦ.ମି. |

Question 7.
ଗୋଟିଏ ଆୟତାକାରକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ 125 ମିଟର ଓ ପ୍ରସ୍ଥ 60 ମିଟର । ଏହାର ଭିତର ପାଖରେ ଦୈର୍ଘ୍ୟର ଗୋଟିଏ ଧାରକୁ ଓ ପ୍ରସ୍ଥର ଦୁଇ ଧାରକୁ ଏହିପରି ତିନି ଧାରକୁ ଲାଗି 2 ମିଟର ଚଉଡ଼ାର ଏକ ରାସ୍ତା ଅଛି । ରାସ୍ତାଟିର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ABCD ଆୟତାକାରକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ = AB = 125 ମି. ଓ ପ୍ରସ୍ଥ = AD = 60 ମି.
∴ କ୍ଷେତ୍ରଟିର ଭିତର ପାଖରେ ରାସ୍ତାଟି ଅଛି ।
EFGH ଆୟତାକାରକ୍ଷେତ୍ରଟିର ଦୈର୍ଘ୍ୟ = EF = (125 – 2 × 2) = 121 ମିଟର
ଓ ପ୍ରସ୍ଥ = EH = 60 – 2 = 58 ମିଟର

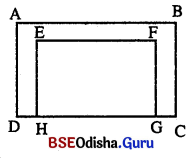
∴ ରାମାର ଯେତ୍ରଫଲ = ABCD ଆୟତାକାରକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ – EFGH
ଆୟତାକାରକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (AB × AD) – (EF × EH)
= (125 × 60) ଦ.ମି. – (121 × 58) ଦ.ମି. = (7500 – 7018) ଦ.ମି. = 482 ଦ.ମି. |

Question 8.
ଗୋଟିଏ ଆୟତାକାର ପଡ଼ିଆର ମଧ୍ୟଭାଗରେ 2 ମିଟର ଚଉଡ଼ାର ଦୁଇଟି ରାସ୍ତା ପରସ୍ପରକୁ ସମକୋଣରେ ଛେଦକରନ୍ତି, ଯେପରିକି ପ୍ରତ୍ୟେକ ରାସ୍ତା ଆୟତାକାର ପଡ଼ିଆର ଗୋଟିଏ ବାହୁ ସହିତ ସମାନ୍ତର । ଆୟତାକାର ପଡ଼ିଆର ଦୈର୍ଘ୍ୟ 72 ମି. ଓ ପ୍ରସ୍ଥ 48 ମି. ହେଲେ, ରାସ୍ତାର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
PORS ଏବଂ EFGH ଦୁଇଗୋଟି ରାସ୍ତା କ୍ଷେତ୍ରଟିର ମଧ୍ୟଭାଗରେ ପରସ୍ପରକୁ ଛେଦକରନ୍ତି ।
ABCD ଆୟତାକାର ପଡ଼ିଆର ଦୈର୍ଘ୍ୟ = AB = 72 ମି. ଓ ପ୍ରସ୍ଥ = BC = 48 ମି.
∴ AB = EF = GH ଏବଂ BC = QR = PS
ରାସ୍ତାର ଚଉରା = 2 ମି. ଅର୍ଥାତ୍ PQ = SR = EH = FG = 2 ମି.
PORS କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ PS × PQ = (48 × 2) = 96 ଦ.ମି.

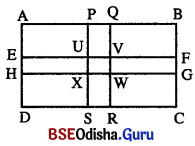
EFGH କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = EF × EH = (72 × 2) = 144 ବ.ମି.
∴ UVWX ର କ୍ଷେତ୍ରଫଳ = UV × UX = (2 × 2) = 4 ବ.ମି.
∴ ରାସ୍ତାର କ୍ଷେତ୍ରଫଳ
= PORS ରାସ୍ତାର କ୍ଷେତ୍ରଫଳ + EFGH ରାସ୍ତାର କ୍ଷେତ୍ରଫଳ – UVWX ର କ୍ଷେତ୍ରଫଳ
= 96 + 144 – 4 = 236 ବ. ମିଟର ।