BSE Odisha 8th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(f)

Odisha State Board BSE Odisha 8th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(f) Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(f)

Question 1.
ନିମ୍ନରେ ରମ୍ବସ୍‌ର କଣ୍ଠଦ୍ଵୟର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଅଛି । ପ୍ରତ୍ୟେକ ସ୍ଥଳରେ କ୍ଷେତ୍ରଫଳ ସ୍ଥିର କର ।
(i) 16 ସେ.ମି. ଓ 20 ସେ.ମି.
(ii) 20 ମି. ଓ 15.4 ମି.
(iii) 8√2 ମି. ଓ 4√2 ମି..
Solution:
ଆମେ ଜାଣିନ୍ତୁ, ଉମ୍ଭପର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × କଣ୍ଠଦ୍ଵୟର ଦୈର୍ଘ୍ୟ ଉମ୍ଭପର
ଏହାର ପ୍ରୟୋଗରେ ପାଇବା :
(i) \(\frac { 1 }{ 2 }\) × 16 × 20 = 160 ଦି ସେ.ମି.
(ii) \(\frac { 1 }{ 2 }\) × 20 × 15.4 = 154 ଦି ମି.
(iii) \(\frac { 1 }{ 2 }\) × 8√2 × 4√2 = 32 ଦି ମି.

Question 2.
ନିମ୍ନରେ ରମ୍ବସ୍‌ର କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଅଛି । ପ୍ରତ୍ୟେକ ସ୍ଥଳରେ ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
(i) 40 ସେ.ମି. ଓ 30 ସେ.ମି.
(ii) 14 ମି. ଓ 48 ମି.
(iii) 1.6 ସେ.ମି. ଓ 30 ସେ.ମି.
(iv) 1.8 ମି ଓ 2.4 ମି.
Solution:

Question 3.
ଗୋଟିଏ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ 840 ବର୍ଗମିଟର । ଏହାର ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ 42 ମିଟର । ଏହାର ଅନ୍ୟ କଣ୍ଠର ଦୈର୍ଘ୍ୟ ଓ ପରିସୀମା ନିର୍ଣ୍ଣୟ କର ।
Solution:
ABCD ରମ୍ବସ୍‌ର କର୍ଣ୍ଣ \(\overline{\mathrm{AC}})\) ଓ BD ପରସ୍ପରକୁ O ବିନ୍ଦୁରେ ସମକୋଣରେ
ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି । BD = 42 ମିଟର (ଦତ୍ତ)
କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ ⇒ 840 = \(\frac { 1 }{ 2 }\)BD.AC
⇒ 840 = \(\frac { 1 }{ 2 }\) × 42 × AC ⇒ AC = \(\frac { 840 }{ 21 }\) = 40 ମିଟର

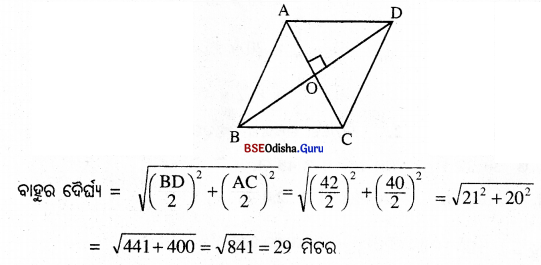
∴ ପରିସୀମା = 4 × ବାହୁ = 4 × 29 = 116 ମିଟର

Question 4.
ଏକ ରମ୍ବସ୍‌ର ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ, ଅନ୍ୟ କର୍ପୂର ଦୈର୍ଘ୍ୟର 3 ଗୁଣ ଏବଂ ଏହାର କ୍ଷେତ୍ରଫଳ 1944 ବର୍ଗମିଟର ହେଲେ, କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ମନେକର ରମ୍ବସ୍‌ର ଗୋଟିଏ x ମି. |
ପ୍ରଶ୍ନନୁସାରେ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 3x ମି. ।

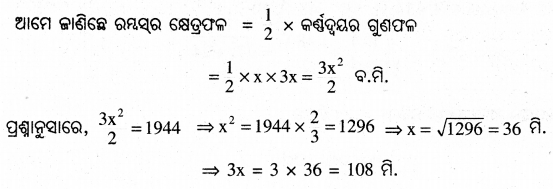
∴ ରମ୍ବସ୍‌ର କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ତମେ 36 ମି. ଓ 108 ମି. |

Question 5.
ଗୋଟିଏ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ 648√ 3 ବର୍ଗ ସେ.ମି. ଓ ଏହାର ଗୋଟିଏ କୋଣର ପରିମାଣ 60° ହେଲେ ଏହାର କ୍ଷୁଦ୍ରତର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ABCD ରମ୍ବସ୍‌ର m∠B = 60° ଏବଂ AB = BC |
∴ ABC ଏକ ସମବାହୁ △ ।
କୋଣର କ୍ଷେତ୍ରଫଳ = 2 × △ABC ର କ୍ଷେତ୍ରଫଳ = 2 × \(\frac{\sqrt{3}}{4}\) × BC²

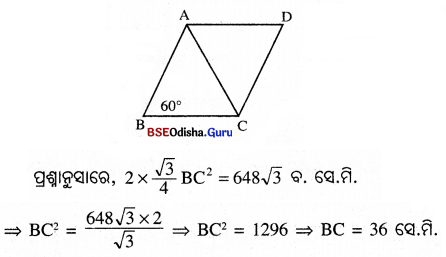
କିନ୍ତୁ ABC ସମବାହ୍ନୁ ହେତୁ ସମ୍ଭପର ପୁତ୍ରତର କଣ୍ଡ AB = AC = 36 ସେ.ମି.
∴ ସମ୍ଭପର ପୁତ୍ରତର ହେତୁ ଦୈର୍ଘ୍ୟ 36 ସେ.ମି.

Question 6.
ଗୋଟିଏ ରମ୍ବସ୍‌ର ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ ତାହାର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟସହ ସମାନ । ରମ୍ବସ୍‌ର ପରିସୀମା 48 ସେ.ମି. ହେଲେ, ତାହାର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ABCD ରମ୍ବସ୍‌ର AB
ଅର୍ଥାତ୍ AB = BC = AC
ABCD ରମ୍ବସ୍‌ର ପରିସୀମା = 48 ସେ.ମି.
∴ ରମ୍ବସ୍‌ର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac{48}{4}\) = 12 ସେ.ମି.

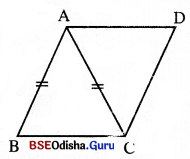
ABCD ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ = 2 × △ABC ର କ୍ଷେତ୍ରଫଳ = 2 × \(\frac{\sqrt{3}}{4}\) × AB² = 2 × \(\frac{\sqrt{3}}{4}\) × (12)²
(∵ ABC ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ଓ ଏହାର ବାହୁର ଦୈର୍ଘ୍ୟ = 12 ସେ.ମି. )
= \(\frac{\sqrt{3}}{2}\) × 144 = 72√3 ବ. ସେ.ମି.
∴ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ = 72√3 ବ. ସେ.ମି.

Question 7.
ଗୋଟିଏ ରମ୍ବସ୍‌ର ପରିସୀମା 16 ମିଟର । ଏହାର ଗୋଟିଏ କଣ୍ଠର ଦୈର୍ଘ୍ୟ 6 ମିଟର ହେଲେ, ଅନ୍ୟ କଣ୍ଠର ଦୈର୍ଘ୍ୟ ଓ କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ରମ୍ବସ୍‌ ପରିସୀମା = 16 ମି.
∴ ରମ୍ବସ୍‌ର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac { 16 }{ 4 }\) = 4 ମି.
ମନେକର ରମ୍ବସ୍‌ର ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 2x ମିଟର

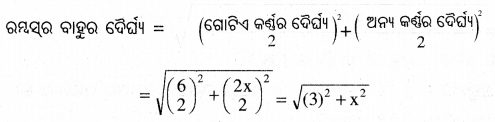
⇒ (କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ)² = (3)² + x² ⇒ (4)² = 9 + x² ⇒ 16 = 9 + x²
= x² = 16 – 9 = 7 ⇒ x = √7 ମିଟର
∴ ଅନ୍ୟ କର୍ଣଟିର ଦୈର୍ଘ୍ୟ = 2 × √7 ମି. = 2√7 ମିଟର
∴ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ = \(\frac { 1 }{ 2 }\) × 6 × 2√7 = 6√7 କର୍ଣ୍ଣଦ୍ୱୟର