Odisha State Board BSE Odisha 8th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(h) Textbook Exercise Questions and Answers.
BSE Odisha Class 8 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(h)
Question 1.
ଗୋଟିଏ ଚତୁରୁକର ଗୋଟିଏ କଣ୍ଡର ଦୈର୍ଘ୍ୟ 78 ସେ.ମି. ଏବଂ ଏହି କଣ୍ଠ ଉପରେ ଏହାର ସମ୍ମୁଖୀନ 23 ସେ.ମି. ଓ 42 ସେ.ମି. ହେଲେ, ଚତୁର୍ଭୁଜଟିର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ABCD ଚତୁର୍ଭୁଜରେ BD = 78 ସେ.ମି. ଏବଂ AM, CN ଯଥାକ୍ରମେ
A ଓ C ବିନ୍ଦୁରୁ BD ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ ।
ଦଉ ଅଛି AM = 23 ସେ.ମି., CN = 42 ସେ.ମି.
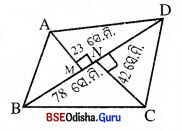
∴ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) BD (AM + CN)
= \(\frac { 1 }{ 2 }\) × 78 (23 + 42) = 39 × 65 = 2535 ବଗ ସେ.ମି.
Question 2.
କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରଛେଦୀ ହୋଇ ନଥିବା ଏକ ଚତୁର୍ଭୁଜର ବହିଃସ୍ଥ କର୍ଷର ଦୈର୍ଘ୍ୟ 43 ସେ.ମି. ଏବଂ ଉକ୍ତ କଣ୍ଠ ଉପରେ ଏହାର ସମ୍ମୁଖୀନ କୌଣିକ ବିନ୍ଦୁଦ୍ଵୟରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ଵୟର ଦୈର୍ଘ୍ୟ 19 ସେ.ମି. ଓ 9 ସେ.ମି. ହେଲେ, ଚତୁର୍ଭୁଜଟିର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ABCD ପ୍ରବୃଦ୍ଧକୋଣୀ ଚତୁର୍ଭୁଜର ବହିଃସ୍ଥ କଣ୍ଠର ଦୈର୍ଘ୍ୟ BD = 43 ସେ.ମି.
AM ଓ CN ଯଥାକ୍ରମେ À ଓ C ବିନ୍ଦୁରୁ BD ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ
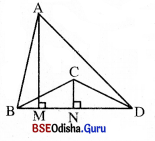
AM = 19 ସେ.ମି. ଏବଂ CN = 9 ସେ.ମି. |
∴ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) BD (AM – CN) = \(\frac { 1 }{ 2 }\) × 43 × (19 – 9) = \(\frac { 1 }{ 2 }\) × 43 × 10 = 215 ଦ. ସେ.ମି.
![]()
Question 3.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର କଣ୍ଠଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ଛେଦକରନ୍ତି । କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 40 ଡେସି.ମି. ଓ 45 ଡେସି.ମି. ହେଲେ, ଏହାର କ୍ଷେତ୍ରଫଳ ନିଶ୍ଚୟ କର ।
Solution:
ଚତୁର୍ଭୁଜର କଣ୍ଠଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ସମଦ୍ୱିଖଣ୍ଡ କରନ୍ତି |
∴ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ = \(\frac { 1 }{ 2 }\) × 40 × 45 = 900 ଦଣ ତେମମିଟର |
Question 4.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି 50 ମିଟର ଓ ସେମାନଙ୍କ ଅନ୍ତର୍ଗତ କୋଣ ସମକୋଣ । ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ ଅନ୍ୟ କର୍ପୂର ଦୈର୍ଘ୍ୟର 4 ଗୁଣ ହେଲେ, ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ ନିଶ୍ଚୟ କର ।
Solution:
ମନେକର କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ x ମି. ଏବଂ 4x ମି.
ପ୍ରଶ୍ନନୁସାରେ x + 4x = 50 ମି. ⇒ 5x = 50 ⇒ x = 10 ମି.
∴ କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ x = 10 ମି. ଏବଂ 4x = 40 ମି. |
କର୍ଣ୍ଣଦ୍ୱୟର ଅନ୍ତର୍ଗତ କୋଣ ସମକୋଣ ହେତୁ,
ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ = \(\frac { 1 }{ 2 }\) × 10 × 40 = 200 ବଗ ମି.
Question 5.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 16 ସେ.ମି., 30 ସେ.ମି., 50 ସେ.ମି. ଓ 52 ସେ.ମି. ଏବଂ ପ୍ରଥମ ବାହୁଦ୍ୱୟର ଅନ୍ତର୍ଗତ କୋଣଟି ସମକୋଣ । ଚତୁର୍ଭୁଜଟିର କ୍ଷେତ୍ରଫଳ ନିର୍ଣୟ କର ।
Solution:
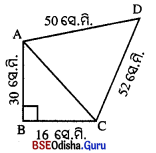
ABCD ଚତୁର୍ଭୁଜର AB = 30 ସେ.ମି.
BC = 16 ସେ.ମି., CD = 52 ସେ.ମି.
AD =50 ସେ.ମି. ଏବଂ m∠ABC = 90°
∴ AC = \(\sqrt{\mathrm{AB}^2+\mathrm{BC}^2}\) = \(\sqrt{30^2+16^2}\) = \(\sqrt{900+256}\) = \(\sqrt{1156}\) = 34 ସେ.ମି.
△ABC ର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) AB × BC = \(\frac { 1 }{ 2 }\) × 30 × 16 = 15 × 16 = 240 ଦ.ସେ.ମି.
△ADCର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ 50 ସେ.ମି., 52 ସେ.ମି. ଏବଂ 34 ସେ.ମି. ।
ଆଦିପରିସାପ = (s) = \(\frac { 50+52+34 }{ 2 }\) = \(\frac { 136 }{ 2 }\) = 68 ସେ.ମି.
∴ ADC ର କ୍ଷେତ୍ରଫଳ =
∴ ABCD ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = △ABCର କ୍ଷେତ୍ରଫଳ + △ADCର କ୍ଷେତ୍ରଫଳ
= 240 + 816 = 1056 ଦ.ସେ.ମି.
Question 6.
କୌଣସି ଚତୁର୍ଭୁଜର ଗୋଟିଏ କୋଣ ସମକୋଣ । ସମକୋଣସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 12 ମି. ଓ 16 ମି. ଏବଂ ଚତୁର୍ଭୁଜର ଅନ୍ୟ ବାହୁର ଦୈର୍ଘ୍ୟ ପ୍ରତ୍ୟେକେ 26 ମି. ହେଲେ, ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
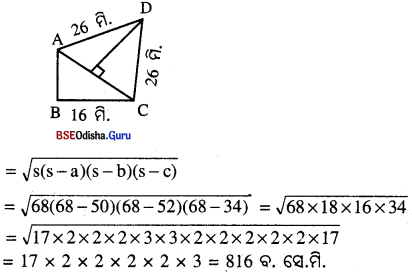
ସମାଧାନ : ABCD ଚତୁର୍ଭୁଜର AB = 12 ମି., BC = 16 Я.
AD = CD = 26 ମିଟର ଏବଂ ZABC = 90° ।
∴ AC = \(\sqrt{\mathrm{AB}^2+\mathrm{BC}^2}\) = \(\sqrt{12^2+16^2}\) = \(\sqrt{144+256}\) = \(\sqrt{400}\) = 20 ମି.
∴ △ABC ର ଯେତ୍ରଫଲ = \(\frac { 1 }{ 2 }\) AB . BC = \(\frac { 1 }{ 2 }\) × 12 × 16 = 96 ଦ. ମି.
△ABC ର ସମାନ ଦାଦୁର ଦେଶ୍ୟ = 26 ମି. କ୍ତମି = AC = 20 ନଗର |
∴ ଭଲତା DM = \(\sqrt{\mathrm{AD}^2-\mathrm{AM}^2}\) = \(\sqrt{26^2-10^2}\) = \(\sqrt{676-100}\) = \(\sqrt{576}\) = 24 ମି.
∴ △ADC ର ଯେତ୍ରଫଲ = \(\frac { 1 }{ 2 }\) AC × DM = \(\frac { 1 }{ 2 }\) × 20 × 24 = 240 ଦ. ମି.
∴ ABCD ଚତୁରୁକର ଯେତ୍ରଫଲ = △ABC ର ଯେତ୍ରଫଲ + △ADC ର ଯେତ୍ରଫଲ
= 96 + 240 = 336 ବଗମିଟର
![]()
Question 7.
ABCD ଚତୁରୁକର AB = 75 ସେ.ମି., BC = 78 ସେ.ମି., CD = 63 ସେ.ମି., DA = 30 ସେ.ମି. ଏବଂ AC = 51 ସେ.ମି. ହେଲେ, ଚତ୍ରରୁଲଗିର ଯେତ୍ରପଲ କିଣ୍ଡସ୍ କର |
Solution:
ABCD ଚତୁରୁକର AB = 75 ସେ.ମି.
BC = 78 ସେ.ମି., CD = 63 ସେ.ମି.,
DA = 30 ସେ.ମି. ଏବଂ AC = 51 ସେ.ମି.
△ABC ର ଆଦିପରିସାମା = s = \(\frac { 75+78+51 }{ 2 }\) = 102 ମି.
∴△ABC ର ଯେତ୍ରଫଲ =

△ADC ର ଯେତ୍ରଫଲ =
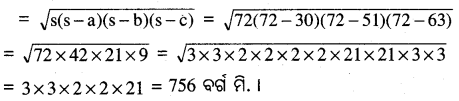
∴ ABCD ଚତୁରୁକର ଯେତ୍ରଫଲ = △ABC ର ଯେତ୍ରଫଲ + △ADC ର ଯେତ୍ରଫଲ
= (1836 + 756) ବଗ ମି. = 2592 ବଗ ମି.
Question 8.
ABCD ଚତୁରୁକର AB = 21 ସେ.ମି., BC = 16 ସେ.ମି., AD = 20 ସେ.ମି. ଓ m∠BAD = m∠CBD = 90° ହେଲେ, ଚତୁରୁକର ଯେତ୍ରଫଲ କିଣ୍ଡସ୍ କର |
Solution:
ABCD ଚତୁରୁକର AD = 20 ସେ.ମି. AB = 21 ସେ.ମି.
BC = 16 ସେ.ମି. ଏବଂ m∠BAD = m∠CBD = 90° |
△DAB ରେ BD = \(\sqrt{\mathrm{AD}^2+\mathrm{AB}^2}\) = \(\sqrt{20^2+21^2}\) = \(\sqrt{400+441}\) = \(\sqrt{841}\) = 29 ସେ.ମି.
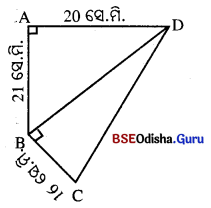
△DAB ର ଯେତ୍ରଫଲ = \(\frac { 1 }{ 2 }\) × 20 × 21 = 210 ଦ. ସେ.ମି.
△CBD ର ଯେତ୍ରଫଲ = \(\frac { 1 }{ 2 }\) × 16 × 29 = 232 ଦ. ସେ.ମି.
∴ ABCD ଚତୁରୁକର ଯେତ୍ରଫଲ = △DAB ର ଯେତ୍ରଫଲ + △CBD ର ଯେତ୍ରଫଲ
= 210 + 232 = 442 ଦ. ସେ.ମି.
Question 9.
ଟିତ୍ରରେ ABCD ଏକ ଚତୁରୁକ | BC = CD ହେଲେ, BC ଓ CD ର ଦେଶ୍ୟ ଏବଂ ABCD ଚତୁରୁକର ଯେତ୍ରଫଲ କିଣ୍ଡସ୍ କର |
Solution:
ABCD ଚତୁରୁକର AB = 3 ମି., AD = 4 ମି.
m∠BAD = m∠BCD = 90°, BC = CD
ABD ସମକୋଣା △ରେ, BD = \(\sqrt{AB^2+AD^2}\) = \(\sqrt{3^2+4^2}\) = \(\sqrt{9+16}\) = \(\sqrt{25}\) = 5 ମି.
BCD ସମକୋଣା ସମଦ୍ୱିବାହୁ △ରେ କଣ୍ଡ BD ର ଦେଶ୍ୟ = 5 ମି.
∴ BC = CD = \(\frac{\mathrm{BD}}{\sqrt{2}}\) = \(\frac{5}{\sqrt{2}}\) ମି.
∴ ABCD ଚତୁରୁକର ଯେତ୍ରଫଲ = △ABD ର ଯେତ୍ରଫଲ + △BCD ର ଯେତ୍ରଫଲ
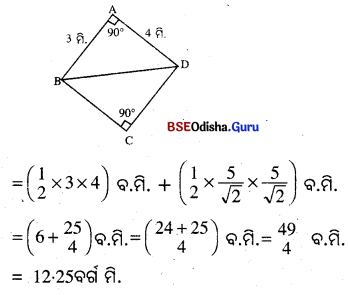
Question 10.
ଚିତ୍ରରେ ∠BAD ଏକ ସମଲୋଗ | AB = 4 ସେ.ମି., AD = 3 ସେ.ମି., DC = 4 ସେ.ମି. ଏବଂ BC = 6 ସେ.ମି. ହେଲେ, ABCD ଚତୁରୁକର ଯେତ୍ରଫଲ କିଣ୍ଡସ୍ କର |
Solution:
ABD ସମଲୋଗ △ରେ
BD = \(\sqrt{\mathrm{AB}^2+\mathrm{AD}^2}\) = \(\sqrt{4^2+3^2}\) = \(\sqrt{25}\) = 5 ସେ.ମି.
∴ △ABD ର ଯେତ୍ରଫଲ = \(\frac { 1 }{ 2 }\) × AB × AD = \(\frac { 1 }{ 2 }\) × 4 × 3 = 6 ଦ. ସେ.ମି.
△BCD ରେ BC = a = 6 ସେ.ମି. BD = b = 5 ସେ.ମି. ଓ CD = c = 4 ସେ.ମି.
△BCD ର ଅଦିପରିସାମା (s) = \(\frac { a+b+c }{ 2 }\) = \(\frac { 6+5+4 }{ 2 }\) = \(\frac { 15 }{ 2 }\) ସେ.ମି. = 7.5 ସେ.ମି.
△BCD ର ଯେତ୍ରଫଲ =
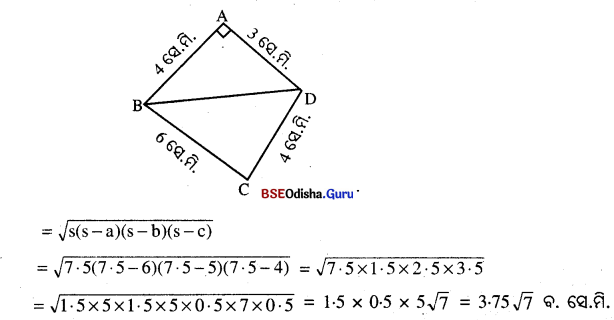
∴ ABCD ଚତୁରୁକର ଯେତ୍ରଫଲ
= △ABD ର ଯେତ୍ରଫଲ + △BCD ର ଯେତ୍ରଫଲ = (6 + 3.75√ 7) ଦ. ସେ.ମି.
= (6 + 3.75 × 2.645) ବଗ ସେ.ମି.
= (6 + 9.918) ବଗ ସେ.ମି.
= 15.918 ବଗ ସେ.ମି. ଦା 15.92 ବଗ ସେ.ମି.
