BSE Odisha 9th Class Maths Notes Geometry Chapter 5 ପରିମିତି

Odisha State Board BSE Odisha 9th Class Maths Notes Geometry Chapter 5 ପରିମିତି will enable students to study smartly.

BSE Odisha Class 9 Maths Notes Geometry Chapter 5 ପରିମିତି

ଉପକ୍ରମଣିକା :
ଯେଉଁ ଶାସ୍ତ୍ରରେ ରେଖାର ଦୈର୍ଘ୍ୟ, କ୍ଷେତ୍ରର ପରିସୀମା, ତଳର କ୍ଷେତ୍ରଫଳ, ଘନବସ୍ତୁର ଆୟତନ ବା ଘନଫଳ ନିର୍ଣ୍ଣୟ କରିବା ପ୍ରଣାଳୀ ସମ୍ବନ୍ଧରେ ଆଲୋଚନା କରାଯାଏ, ତାହାକୁ ପରିମିତି (Mensuration) କୁହାଯାଏ ।
(i) ବିଭିନ୍ନ ଆବଦ୍ଧକ୍ଷେତ୍ରମାନଙ୍କ ପରିମାପରୁ ପରିମିତି ବିଷୟଟିର ସୃଷ୍ଟି ହୋଇଥିଲା । ଗଣିତର ଏହା ଏକ ଅତି ପ୍ରାଚୀନ ବିଷୟଭାବେ ପରିଚିତ । ପରିମିତି ବିଷୟଟି ଜ୍ୟାମିତିକ ଧାରଣା ଓ ତଥ୍ୟ ଉପରେ ନିର୍ଭରଶୀଳ ।
(ii) ଏଠାରେ ବିଭିନ୍ନ ଆକାରର କ୍ଷେତ୍ରମାନଙ୍କ କ୍ଷେତ୍ରଫଳ ଓ ପରିସୀମା ନିର୍ଣ୍ଣୟ କରାଯାଏ । ଏତଦ୍ ବ୍ୟତୀତ ଘନବସ୍ତୁମାନଙ୍କ ଘନଫଳ ଓ ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ମଧ୍ଯ ନିରୂପଣ କରାଯାଇଥାଏ ।
(iii) ଆମ ଆଲୋଚନା ଅନ୍ତର୍ଗତ ସମସ୍ତ କ୍ଷେତ୍ର ସମତଳରେ ଅବସ୍ଥିତ। ସୁତରାଂ ଏହି କ୍ଷେତ୍ରଗୁଡ଼ିକୁ ସାମତଳିକ କ୍ଷେତ୍ର କୁହାଯାଏ । ପୁନଶ୍ଚ କ୍ଷେତ୍ରମାନେ ସରଳରେଖାମାନଙ୍କଦ୍ୱାରା ଆବଦ୍ଧ ।

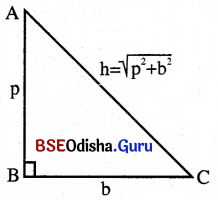
ପିଥାଗୋରାସ୍ ଉପପାଦ୍ୟ (Pythagoras Theorem) :
{ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟର ବର୍ଗ ଏହାର ଅନ୍ୟ ଦୁଇବାହୁର ଦୈର୍ଘ୍ୟର ବର୍ଗର ସମଷ୍ଟି ସହିତ ସମାନ ।}
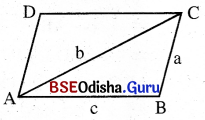
(i) ABC ସମକୋଣୀ ତ୍ରିଭୁଜରେ ∠ABC ସମକୋଣ । ସମକୋଣର ସମ୍ମୁଖୀନ ବାହୁକୁ କଣ୍ଠ ଓ ଅନ୍ୟ ଦୁଇବାହୁ A͞B ଓ B͞C ଙ୍କ ମଧ୍ୟରୁ ଗୋଟିକୁ ଭୂମି (Base) ଓ ଅନ୍ୟଟିକୁ ଲମ୍ବ (Perpendicular) କୁହାଯାଏ । 
(ii) ତ୍ରିଭୁଜର ∠A କୋଣ ପାଇଁ B͞C କୁ ଲମ୍ବ ଏବଂ A͞B କୁ ଭୂମି କୁହାଯାଏ । କିନ୍ତୁ ∠C ପାଇଁ A͞B କୁ ଲମ୍ବ ଓ B͞C କୁ ଭୂମି କୁହାଯାଏ । ଅର୍ଥାତ୍ ସମକୋଣ ବ୍ୟତୀତ ଯେକୌଣସି କୋଣପାଇଁ ତାହା ସହିତ ସଂଲଗ୍ନ ବାହୁକୁ ଭୂମି ଓ କୋଣର ସମ୍ମୁଖୀନ ବାହୁକୁ ଲମ୍ବ କୁହାଯାଏ ।
(iii) ଲମ୍ବ, ଭୂମିର ଦୈର୍ଘ୍ୟ ଓ କଣ୍ଠର ଦୈର୍ଘ୍ୟକୁ ଯଥାକ୍ରମେ p, b ଓ h ଦ୍ବାରା ସୂଚିତ ଉପପାଦ୍ୟ ଅନୁସାରେ, AC² = AB² + BC² ଅର୍ଥାତ୍ h² = p² + b²

ପିଥାଗୋରାସ୍ ଉପପାଦ୍ୟର ବିପରୀତ ଉପପାଦ୍ୟ :
କୌଣସି ତ୍ରିଭୁଜର ଏକ ବାହୁର ଦୈର୍ଘ୍ୟର ବର୍ଗ ତାହାର ଅନ୍ୟ ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟର ବର୍ଗର ସମଷ୍ଟି ସହସମାନ ହେଲେ, ତ୍ରିଭୁଜଟି ସମକୋଣୀ । ଅର୍ଥାତ୍ ΔABCରେ AC² = AB² + BC² ହେଲେ m∠B = 90° ହେବ ।

• ଗୋଟିଏ ଆୟତକ୍ଷେତ୍ରର ପ୍ରତ୍ୟେକ କୋଣ ସମକୋଣ, ତେଣୁ ଏହାର ସମକୋଣ ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ a ଏକକ ଓ b ଏକକ ହେଲେ, ପ୍ରତ୍ୟେକ କଣ୍ଠର ଦୈର୍ଘ୍ୟ = \(\sqrt{a^2+b^2}\) ଏକକ ।
• ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ a ଏକକ ହେଲେ, ବର୍ଗକ୍ଷେତ୍ରର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = √2 a ଏକକ ।
• ସମବାହୁ ତ୍ରିଭୁଜର ଉଚ୍ଚତା = \(\frac{\sqrt{3}}{2}\) × ବାହୁର ଦୈର୍ଘ୍ୟ ଏବଂ ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac{\sqrt{2}}{3}\) × ଉଚ୍ଚତା ।

ସରଳରେଖକ କ୍ଷେତ୍ର ଓ ଏହାର କ୍ଷେତ୍ରଫଳ (Polygonal region and its area) :
ପରସ୍ପରର ଅନ୍ତର୍ଦେଶକୁ ଛେଦ କରୁନଥ‌ିବା ସସୀମ ସଂଖ୍ୟକ ତ୍ରିଭୁଜାକାର କ୍ଷେତ୍ରର ସଂଯୋଗକୁ ଏକ ବହୁଭୁଢାକାର ବା ସରଳରେଖକ କ୍ଷେତ୍ର (Polygon region) କୁହାଯାଏ ।
କ୍ଷେତ୍ରଫଳ ସ୍ଵୀକାର୍ଯ୍ୟ (Area Postulates) :

• ଗୋଟିଏ ସରଳରେଖ୍କ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଧନାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା ।
• ଦୁଇଟି ସର୍ବସମ ଆବଦ୍ଧକ୍ଷେତ୍ର (ତ୍ରିଭୁଜ)ର କ୍ଷେତ୍ରଫଳ ସମାନ ।
• ଗୋଟିଏ ସରଳରୈଖ୍କ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ଏହାକୁ ଗଠନ କରୁଥିବା ତ୍ରିଭୁଜମାନଙ୍କ କ୍ଷେତ୍ରଫଳର ସମଷ୍ଟି ସହ ସମାନ । 

ଚତୁର୍ଭୁଜ ଓ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ ସମ୍ବନ୍ଧୀୟ ସୂତ୍ରାବଳୀ :
(1) ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ a ଏକକ ଓ ପ୍ରସ୍ଥ b ଏକକ ହେଲେ
ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଦୈର୍ଘ୍ୟ × ପ୍ରସ୍ଥ = ab ବର୍ଗ ଏକକ ।
(2) ବର୍ଗକ୍ଷେତ୍ରର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ a ଏକକ ହେଲେ, ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = a² ବର୍ଗ ଏକକ ।
(3) ଗୋଟିଏ ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ b ଏକକ ଓ ଉଚ୍ଚତା h ଏକକ ହେଲେ, ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) bh ବର୍ଗ ଏକକ । 
(4) ସମକୋଣୀ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) (ସମକୋଣର ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ)
(5) ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{\sqrt{3}}{4}\) × (ବାହୁର ଦୈର୍ଘ୍ୟ) ବର୍ଗ ଏକକ
⇒ ସମବାହୁ ତ୍ରିଭୁଜର ଉଚ୍ଚତା = \(\frac{\sqrt{3}}{2}\) × ବାହୁର ଦୈର୍ଘ୍ୟ
⇒ ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac{2}{\sqrt{3}}\) × ଉଚ୍ଚତା
⇒ ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{\sqrt{3}}\) × (ଉଚ୍ଚତା)² ବର୍ଗ ଏକକ ।
(6) ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ a, b, c ଏକକ ହେଲେ, ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\sqrt{s(s-a)(s-b)(s-c)}\) ବର୍ଗ ଏକକ (ଯେଉଁଠାରେ a + b + c = 2s) ଏହାକୁ Herronଙ୍କ ସୂତ୍ର କୁହାଯାଏ ।

ସାମାନ୍ତରିକ କ୍ଷେତ୍ର (Parallelogram):
ଯେକୌଣସି ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର
(i) ସମ୍ମୁଖୀନ ବାହୁଗୁଡ଼ିକ ପରସ୍ପର ସର୍ବସମ;
(ii) ସମ୍ମୁଖୀନ କୋଣମାନ ପରସ୍ପର ସର୍ବସମ;
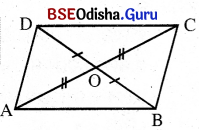
(iii) କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି;
{ଯେଉଁ ଚତୁର୍ଭୁଜର ବିପରୀତ ବାହୁମାନ ସମାନ୍ତର,}
{ତାହାକୁ ସାମାନ୍ତରିକ ଚିତ୍ର କୁହାଯାଏ ।}
(iv) ପ୍ରତ୍ୟେକ କର୍ଣ୍ଣ ପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ପରସ୍ପର ସମାନ ।
(v) ପ୍ରତ୍ୟେକ କଣ୍ଠ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରକୁ ଦୁଇଟି ସର୍ବସମ ତ୍ରିଭୁଜରେ ବିଭକ୍ତ କରେ; ତେଣୁ ଉତ୍ପନ୍ନ ତ୍ରିଭୁଜଦ୍ୱୟର କ୍ଷେତ୍ରଫଳ ସମାନ ଏବଂ
(vi) କର୍ଣ୍ଣଦ୍ଵୟ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରକୁ ଯେଉଁ ଚାରୋଟି ତ୍ରିଭୁଜରେ ବିଭକ୍ତ କରନ୍ତି ସେମାନଙ୍କର କ୍ଷେତ୍ରଫଳ ପରସ୍ପର ସମାନ ।

କ୍ଷେତ୍ରଫଳ :
ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ
(i) ଭୂମିର ଦୈର୍ଘ୍ୟ ଓ ଉଚ୍ଚତା ଦତ୍ତ ଥିଲେ,

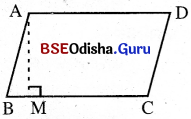
{ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଭୂମିର ଦୈର୍ଘ୍ୟ × ଉଚ୍ଚତା}
ABCD ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = BC × AM

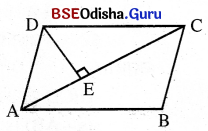
(ii) ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ ଓ ଯେକୌଣସି ସମ୍ମୁଖୀନ କୌଣିକ ବିନ୍ଦୁରୁ କର୍ଣ୍ଣପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ
{ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଗୋଟିଏ କଣ୍ଠର ଦୈର୍ଘ୍ୟ × ସେହି କଣ୍ଠ}
{ପ୍ରତି ଯେକୌଣସି ସମ୍ମୁଖୀନ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ । }
ABCD ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = AC × DE 

(iii) ଦୁଇଟି ସନ୍ନିହିତ ବାହୁର ଦୈର୍ଘ୍ୟ ଓ ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ-
ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 2 × A ABCର କ୍ଷେତ୍ରଫଳ 
=2\(\sqrt{s(s-a)(s-b)(s-c)}\) ବର୍ଗ ଏକକ ।
(ଯେଉଁଠାରେ BC = a ଏକକ, AC = b ଏକକ ଓ AB = c ଏକକ)

(iv) କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଓ ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ-
{ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = କ୍ଷେତ୍ରର ଦୁଇ କଣ୍ଠର ଅଧା ଓ ଗୋଟିଏ ବାହୁ ଦ୍ବାରା ଗଠିତ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳର ଚାରିଗୁଣ ।}
ABCD ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ  = 4 × Δ AOBର କ୍ଷେତ୍ରଫଳ ।

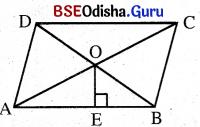
(v) ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ ଓ କର୍ଣ୍ଣଦ୍ୱୟର ଛେଦବିନ୍ଦୁରୁ ଉକ୍ତ ବାହୁ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ-
{ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଏହାର ବାହୁର ଦୈର୍ଘ୍ୟ x କର୍ଣ୍ଣଦ୍ୱୟର ଛେଦବିନ୍ଦୁରୁ ଏଥପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ ଗୁଣଫଳର ଦୁଇଗୁଣ ।}
ABCD ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 2 AB × OE
କାରଣ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 4 × Δ AOBର କ୍ଷେତ୍ରଫଳ = 4 × \(\frac{1}{2}\) AB × OE = 2AB × OE

ରମ୍ବସ୍ (Rhombus) :
ଯେଉଁ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଚାରୋଟିଯାକ ବାହୁ ସର୍ବସମ, ତାହାକୁ ରୟସ୍ କୁହାଯାଏ । ଯେକୌଣସି ରମ୍ବସ୍‌ – 

• ଚାରିବାହୁର ଦୈର୍ଘ୍ୟ ସମାନ ।
• କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରନ୍ତି ।
• ଗୋଟିଏ କଣ୍ଠ ଏହାକୁ ଦୁଇଟି ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ତ୍ରିଭୁଜରେ ପରିଣତ କରେ ।
• କଣ୍ଠଦ୍ଵୟ ଏହାକୁ ଚାରିଗୋଟି ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ସମକୋଣୀ ତ୍ରିଭୁଜରେ ପରିଣତ କରେ ।

ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ :
(1) ବାହୁର ଦୈର୍ଘ୍ୟ ଓ ଉଚ୍ଚତା ଦତ୍ତ ଥିଲେ, 
{ରମ୍ବସର କ୍ଷେତ୍ରଫଳ = ବାହୁର ଦୈର୍ଘ୍ୟ × ଉଚ୍ଚତା}
{ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac{କ୍ଷେତ୍ରଫଳ}{ଉଚ୍ଚତା}\) ଓ ଉଚ୍ଚତା = \(\frac{କ୍ଷେତ୍ରଫଳ}{ବାହୁର ଦୈର୍ଘ୍ୟ}\)}
(2) ରମ୍ବସର କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ,
{ରମ୍ବସର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ ।

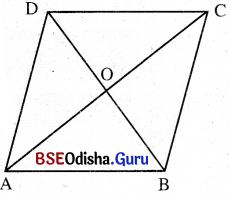
(3) ରମ୍ବସ୍‌ କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ d₁ ଓ d₂ ଏକକ ଦତ୍ତ ଥିଲେ, ବାହୁର ଦୈର୍ଘ୍ୟ \(\sqrt{\left(\frac{d_1}{2}\right)^2+\left(\frac{d_2}{2}\right)^2}\) ଅଥବା \(\frac{1}{2} \sqrt{d_1^2+d_2^2}\)
(ଯେଉଁଠାରେ ରମ୍ବସ୍‌ର କଣ୍ଠଦ୍ଵୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ d₁ ଓ d₂)

ଟ୍ରାପିଜିୟମ୍‌ (Trapezium) :
(i) ଯେଉଁ ଚତୁର୍ଭୁଜର କେବଳ ଦୁଇଟି ବିପରୀତ ବାହୁ ସମାନ୍ତର ତାହାକୁ ଟ୍ରାପିଜିୟମ୍ କୁହାଯାଏ । ଏହାର ଦୁଇ ସମାନ୍ତର ବାହୁ ମଧ୍ୟରେ ଥ‌ିବା ବ୍ୟବଧାନକୁ ଟ୍ରାପିଜିୟମ୍‌ର ଉଚ୍ଚତା କୁହାଯାଏ । ABCD ଟ୍ରାପିଜିୟମ୍‌ରେ \(\overline{\mathrm{AB}} \| \overline{\mathrm{CD}}\) A ବିନ୍ଦୁରୁ C͞D ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ A͞E ହେଲେ, A͞E କୁ ସମାନ୍ତର ବାହୁଦ୍ୱୟ ମଧ୍ୟରେ ବ୍ୟବଧାନ ବା ଟ୍ରାପିଜିୟମ୍‌ର ଉଚ୍ଚତା କୁହାଯାଏ ।

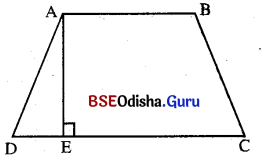
(ii) ଟ୍ରାପିଜିୟମ୍‌ର ଅସମାନ୍ତର ବାହୁଦ୍ୱୟର ମଧ୍ୟବିନ୍ଦୁକୁ ଯୋଗକରୁଥିବା ସରଳରେଖାଖଣ୍ଡ-
(a) ସମାନ୍ତରବାହୁମାନଙ୍କ ସହ ସମାନ୍ତର 
(b) ସମାନ୍ତରବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟିର ଅର୍ଦ୍ଧେକ
(c) ଉଚ୍ଚତାକୁ ଦୁଇଟି ସମଅଂଶରେ ବିଭକ୍ତ କରେ ।
(iii) ଟ୍ରାଫିଜିୟମ୍‌ର ଅସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ ହେଲେ –
(a) ଏହାର କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ 
(b) ପ୍ରତ୍ୟେକ ସମାନ୍ତର ବାହୁ ସଂଲଗ୍ନ କୋଣଦ୍ଵୟ ସର୍ବସମ । 

ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ :
(i) ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଓ ଉଚ୍ଚତା ଦତ୍ତ ଥିଲେ,
ଟ୍ରାଫିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ  = \(\frac{1}{2}\) × ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି × ଉଚ୍ଚତା ।
(ii) ଅସମାନ୍ତର ବାହୁଦ୍ୱୟର ମଧ୍ୟବିନ୍ଦୁକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡର ଦୈର୍ଘ୍ୟ ଓ ଉଚ୍ଚତା ଦତ୍ତ ଥିଲେ,
ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = ଅସମାନ୍ତର ବାହୁଦ୍ୱୟର ମଧ୍ୟବିନ୍ଦୁକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡର ଦୈର୍ଘ୍ୟ × ଉଚ୍ଚତା

ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ :
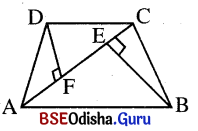
(i) ଚତୁର୍ଭୁଜର ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ ଏବଂ ସେହି କଣ୍ଠପ୍ରତି ସମ୍ମୁଖୀନ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ,
ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × କର୍ପୂର ଦୈର୍ଘ୍ୟ × ଲମ୍ବନ୍ବୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି ।
ABCD ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) AC (DF + BE)

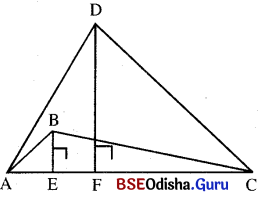
(ii) ଉତ୍ତଳ ହୋଇ ନଥ‌ିବା ଚତୁର୍ଭୁଜର ବହିଃସ୍ଥ କଣ୍ଠର ଦୈର୍ଘ୍ୟ ଓ ଏଥପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବ ଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ,
ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ବହିଃସ୍ଥ କଣ୍ଠର ଦୈର୍ଘ୍ୟ × ବିପରୀତ
କୌଣିକ ବିନ୍ଦୁରୁ ଏଥପ୍ରତି ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଅନ୍ତର
ABCD ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × AC × (DF – BE)

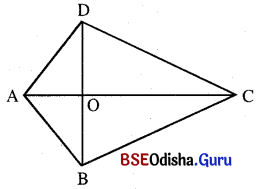
(iii) ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ଛେଦ କରୁଥିଲେ,
ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ  = \(\frac{1}{2}\) × କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳର
ABCD ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) AC × BD 

(iv) ଚତୁର୍ଭୁଜର ଚାରି ବାହୁର ଦୈର୍ଘ୍ୟ ଓ ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ,
ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = Δ ABD କ୍ଷେତ୍ରଫଳ + Δ BCDର କ୍ଷେତ୍ରଫଳ ।

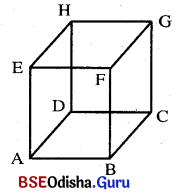
ଘନବସ୍ତୁ (Solids) :

• ଆମ ଦୈନନ୍ଦିନ ଜୀବନରେ ଯେଉଁ ବିଭିନ୍ନ ପ୍ରକାର ବସ୍ତୁ ଦେଖୁ ସେଗୁଡ଼ିକ ଦ୍ବିମାତ୍ରିକ (Two Dimensional) ନୁହନ୍ତି । ଖଣ୍ଡିଏ ଇଟାକୁ ଘରର ଚଟାଣ (ଯାହାକି ଏକ ସମତଳ) ଉପରେ ରଖିଲେ ଇଟାର ଗୋଟିଏ ପାର୍ଶ୍ଵକୁ ଛାଡ଼ିଦେଲେ ଅନ୍ୟ କୌଣସି ଅଂଶ ଚଟାଣରେ ରହିବ ନାହିଁ । ଏହି ପ୍ରକାର ବସ୍ତୁ ଯଥା ଇଟା, ବହି, ବାକ୍ସ, ଗୋଲକ, କୋନ୍ ଇତ୍ୟାଦି ଘନବସ୍ତୁ (Solids) ଅଟନ୍ତି । ଏହି ବସ୍ତୁଗୁଡ଼ିକ ତ୍ରିମାତ୍ରିକ (Three Dimensional) ।
• ତ୍ରିମାତ୍ରିକ ବସ୍ତୁ ପାଇଁ ପରିମିତିରେ ଘନଫଳ ଓ ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ସଂପର୍କରେ ଆଲୋଚନା କରାଯାଇଥାଏ । ଆମେ ଯେଉଁ ତ୍ରିମାତ୍ରିକ ବସ୍ତୁଦ୍ଵୟର ଆଲୋଚନା କରିବା ସେଗୁଡ଼ିକ ହେଲେ ଆୟତଘନ (Cuboid) ଓ ସମଘନ (Cube) ଇଟା ଖଣ୍ଡ ଆୟତଘନର ଉଦାହରଣ ଓ ଲୁଡୁଗୋଟି ସମଘନର ଉଦାହରଣ ।
• ଏଠାରେ ଉଲ୍ଲେଖ ଯୋଗ୍ୟ ଯେ ଚଟାଣରେ ରଖାଯାଇଥିବା ଇଟାଖଣ୍ଡକୁ ଚଟାଣ ସହ ସମାନ୍ତର ଏକ ସମତଳ ଦ୍ଵାରା ଛେଦକଲେ ସମତଳସ୍ଥ ଛେଦଟି ଏକ ଆୟତକ୍ଷେତ୍ର ଓ ସେହିପରି ଲୁଡୁଗୋଟି କ୍ଷେତ୍ରରେ ସମତଳସ୍ଥ ଛେଦଟି ଏକ ବର୍ଗକ୍ଷେତ୍ର ହେବ ।

ଆୟତଘନ ଓ ସମଘନର ଘନଫଳ ଓ ପୃଷ୍ଟତଳର କ୍ଷେତ୍ରଫଳ :
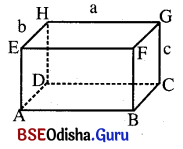
ଆୟତଘନ (Cuboid) :
ଆୟତଘନ ଛଅଗୋଟି ପୃଷ୍ଠତଳ ବିଶିଷ୍ଟ ଏକ ଘନବସ୍ତୁ ଯାହାର ପ୍ରତ୍ୟେକ ପୃଷ୍ଠତଳ ଗୋଟିଏ ଗୋଟିଏ ଆୟତକ୍ଷେତ୍ର ଏବଂ ସମ୍ମୁଖୀନ ପୃଷ୍ଠତଳଦ୍ଵୟ ସମାନ୍ତର ଓ ସର୍ବସମ ଆୟତକ୍ଷେତ୍ର ଅଟନ୍ତି ।
ଆୟତଘନର ଦୈର୍ଘ୍ୟ = a ଏକକ, ପ୍ରସ୍ଥ = b ଏକକ ଓ ଉଚ୍ଚତା = c ଏକକ ହେଲେ
(i) ଆୟତଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2 (ab + bc + ac) ବର୍ଗ ଏକକ ।
(ii) ଆୟତଘନର ପାର୍ଶ୍ଵ ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2(a + b) c ବର୍ଗ ଏକକ । 
(iii) ଆୟତିଙ୍ଘନର ଘନଫଳ = ଯେକୌଣସି ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ × ସେହି ପୃଷ୍ଠତଳ ପ୍ରତି ଲମ୍ବ ଭାବେ ଅବସ୍ଥିତ ଧାରର ଦୈର୍ଘ୍ୟ ।
(iv) ଆୟତଘନର ଘନଫଳ = (ଦୈର୍ଘ୍ୟ × ପ୍ରସ୍ଥ × ଉଚ୍ଚତା) ଘନ ଏକକ

ସମଘନ (Cube) :
ସମଘନ ଏକ ଆୟତଘନ, ଯାହାର ଦୈର୍ଘ୍ୟ, ପ୍ରସ୍ଥ ଓ ଉଚ୍ଚତା ସମାନ । ଅର୍ଥାତ୍ ଯେଉଁ ଆୟତଘନର ସମସ୍ତ ପାର୍ଶ୍ବ ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଗୋଟିଏ ଗୋଟିଏ ବର୍ଗଚିତ୍ର, ତାହା ସମଘନ ଅଟେ ।
ସମଘନରେ ସମସ୍ତ ବାହୁର ଦୈର୍ଘ୍ୟ = a ଏକକ ହେଲେ
(i) ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 6a² ବର୍ଗ ଏକକ । 
(ii) ସମଘନର ପାର୍ଶ୍ଵ ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 4a² ବର୍ଗ ଏକକ
(iii) ସମଘନର ଘନଫଳ = a³ ଘନ ଏକକ ।