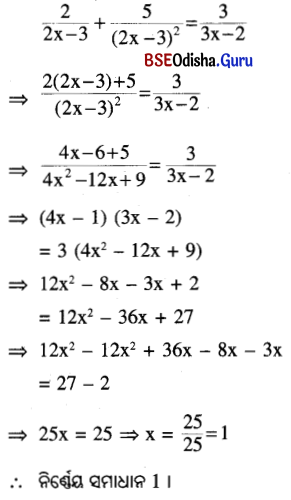BSE Odisha 9th Class Maths Solutions Algebra Chapter 4 ବୀଜଗାଣିତିକ ସମୀକରଣ Ex 4(a)

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 4 ବୀଜଗାଣିତିକ ସମୀକରଣ Ex 4(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 4 ବୀଜଗାଣିତିକ ସମୀକରଣ Ex 4(a)

Question 1.
2, 3, 5, 8 ଓ – 1 ମାନଗୁଡ଼ିକ ମଧ୍ୟରୁ ଅଜ୍ଞାତ ରାଶିର କେଉଁ ଏକ ବା ଏକାଧ୍ଵ ମାନ ଦ୍ୱାରା ସମୀକରଣଟି ସିଦ୍ଧ ହେବ ନିର୍ଣ୍ଣୟ କର ।

(i) (x + 1)² – 2x = x² + 1
ସମାଧାନ:
(x + 1)² – 2x = x² + 1, ବାମପାର୍ଶ୍ଵ = (x + 1)² – 2x = x² + 1 + 2x – 2x = x² + 1 = ଦକ୍ଷିଣପାର୍ଶ୍ବ
ଏହାର ବାମପାର୍ଶ୍ଵ ଦକ୍ଷିଣପାର୍ଶ୍ବ ସହ ସମାନ । ତେଣୁ xର ସମସ୍ତ ମାନ ପାଇଁ ଏହି ସମୀକରଟି ସିଦ୍ଧ ହେବ ।

(ii) 6 (2y – 1) – 5 (y + 3) = 3 (y + 5) – 24
ସମାଧାନ:
6 (2y – 1) – 5 (y + 3) = 3 (y + 5) – 24
⇒ 12y – 6 – 5y – 15 = 3y + 15 – 24
⇒ 7y – 21 = 3y – 9 ⇒ 4y = 12 ⇒ y = 3
ଏଠାରେ yର ମାନ 3 ଅଟେ । କାରଣ y ପରିବର୍ତ୍ତେ 3 ନେଲେ ବାମପାର୍ଶ୍ଵ ଦକ୍ଷିଣପାର୍ଶ୍ଵ ସହ ସମାନ ହେବ ।

(iii) (3 – z) + 2 (1 + z) = 13 – 2 (z + 1)
ସମାଧାନ:
(3 – z) + 2 (1 + z) = 13 – 2 (z + 1)
⇒ 3 – z + 2 + 2z = 13 – 2z – 2
⇒ z + 5 = 11 – 2z ⇒ 3z = 6 ⇒ z = 2
ଏଠାରେ z ର ମାନ 2 ଅଟେ । କାରଣ z ପରିବର୍ତ୍ତେ 2 ବସାଇଲେ ବାମପାର୍ଶ୍ଵ ଦକ୍ଷିଣପାର୍ଶ୍ବ ସହ ସମାନ ହେବ ।

(iv) 6x + 10 = 2 (x + 12) + 9 (x – 1)
ସମାଧାନ:
6x + 10 = 2 (x + 12) + 9 (x – 1)
⇒ 6x + 10 = 2x + 24 + 9x – 9
⇒ 11x + 15 = 6x + 10
⇒ 5x = -5 ⇒ x = -1
ଏଠାରେ x ର ମାନ -1 ଅଟେ । କାରଣ x ପରିବର୍ତ୍ତେ -1 ବସାଇଲେ ବାମପାର୍ଶ୍ଵ ଦକ୍ଷିଣପାର୍ଶ୍ବ ସହ ସମାନ ହେବ ।

(v) 3 (x – 4) + 6 = 2 (x + 2) – 2
ସମାଧାନ:
3 (x – 4) + 6 = 2 (x + 2) – 2
⇒ 3x – 12 + 6 = 2x + 4 – 2
⇒ 3x-6 = 2x + 2 ⇒ x = 8
ଏଠାରେ x ର ମାନ 8 ଅଟେ । କାରଣ x ପରିବର୍ତ୍ତେ 8 ବସାଇଲେ ବାମପାର୍ଶ୍ଵ ଦକ୍ଷିଣପାର୍ଶ୍ବ ସହ ସମାନ ହେବ ।

(vi) 3x + 9 – (3x – 5) – (5x + 4) = 0
ସମାଧାନ:
3x + 9- (3x – 5) – (5x + 4) = 0
⇒ 3x + 9 – 3x + 5 – 5x – 4 = 0
⇒ -5x = -10 ⇒ x = 2
ବି.ଦ୍ର.: ଅଜ୍ଞାତ ରାଶି ପରିବର୍ତ୍ତେ 2, 3, 5, 8 ଓ – 1 ନେଇ ପରୀକ୍ଷା କରି ଦର୍ଶାଯାଇ ପାରେ ଯେ,
ଅଜ୍ଞାତ ରାଶିର କେଉଁ ମାନ ବା କେଉଁ ମାନଗୁଡ଼ିକ ପାଇଁ ସମୀକରଣଟି ସିଦ୍ଧ ।
ଏଠାରେ xର ମାନ 2 ଅଟେ । କାରଣ xର ମାନ 2 ବସାଇଲେ ବାମପାର୍ଶ୍ଵ ଦକ୍ଷିଣପାର୍ଶ୍ବ ସହ ସମାନ ହେବ ।

Question 2.
ନିମ୍ନଲିଖ ସମୀକରଣମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁଟି ସଙ୍ଗତ, କେଉଁଟି ଅସଙ୍ଗତ, କେଉଁଟି ଅଭେଦ ଓ କେଉଁମାନେ ଅନୁରୂପ ନିର୍ଣ୍ଣୟ କର ।

(i) (5x – 1)³ = 125x³ – 15x (5x – 1) – 1
ସମାଧାନ:
(5x – 1)³ = 125 x³ – 15x (5x – 1) – 1
⇒ (5x – 1)³ = (5x – 1)³
∴ ବାମପାର୍ଶ୍ବ = ଦକ୍ଷିଣପାର୍ଶ୍ଵ, ତେଣୁ ଏହା ଏକ ଅଭେଦ ଅଟେ ।

(ii) (x – 5)² = 2 (x – 3) + (x + 2) (x – 2) – 1
ସମାଧାନ:
(x – 5)² = 2(x – 3) + (x + 2) (x – 2) – 1
⇒ x² – 10x + 25 = 2x – 6 + x² – 4 – 1 ⇒ -10x – 2x = -25 – 11
⇒ -12x = -36 ⇒ x = \(\frac{36}{12}\) = 3
∴ ଏହି ସମୀକରଣଟି ସଙ୍ଗତ ଅଟେ ।

(iii) 4x + 3 – (11x – 18) = 0
ସମାଧାନ:
4x + 3 – (11x – 18) = 0 ⇒ 4x + 3 – l11x + 18 = 0
⇒ – 7x + 21 = 0 ⇒ 7x = 21 ⇒ x = \(\frac{21}{7}\) = 3
∴ ଏହି ସମୀକରଣଟି ସଙ୍ଗତ ଅଟେ ଏବଂ ଏହା (ii)ର ଅନୁରୂପ ଅଟେ ।

(iv) 3 (x + 3) (x – 5) = (x – 3)² + (x – 6) (x + 6) + (x + 3) (x – 3) – 9
ସମାଧାନ:
3 (x + 3) (x- 5) = (x – 3)² + (x – 6) (x + 6) + (x + 3) (x – 3) – 9
⇒ 3 (x² – 5x + 3x – 15) = x² – 6x + 9 + x² – 36 + x² – 9 – 9
⇒ 3x² – 6x – 45 = 3x² – 6x – 45
∴ ଏହି ସମୀକରଣଟିରେ ବାମପାର୍ଶ୍ବ = ଦକ୍ଷିଣପାର୍ଶ୍ବ । ତେଣୁ ଏହା ଏକ ଅଭେଦ ଅଟେ ।

(v) 3 (x + 2a) – 2b = 2 (x + a) + b
ସମାଧାନ:
3 (x + 2a) – 2b = 2 (x + a) + b ⇒ 3x + 6a – 2b = 2x + 2a + b
⇒ 3x – 2x + 6a – 2a = b + 2b ⇒ x + 4a = 3b ⇒ x = 3b – 4a
∴ xର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ମାନ ପାଇଁ ସିଦ୍ଧ ହେଉଥ‌ିବାରୁ ଏହା ଏକ ସଙ୍ଗତ ସମୀକରଣ ଅଟେ ।

(vi) 3 (x + 2) = 4 (2x – 1) – 5 (x + 3)
ସମାଧାନ:
3 (x + 2) = 4 (2x – 1) – 5 (x + 3) ⇒ 3x + 6 = 8x – 4 – 5x – 15
⇒ 3x – 8x + 5x = -19 – 6 ⇒ 8x – 8x = -25 ⇒ 0 = -25
∴ xର ମାନ ନିର୍ଣ୍ଣୟ ଅସମ୍ଭବ ହେତୁ ଏହି ସମୀକରଣଟି ଅସଙ୍ଗତ ଅଟେ ।

Question 3.
ସମାଧାନ କର :

(i) 2 (3x – 1) – 3(x + 2) = 1
ସମାଧାନ:
2 (3x – 1)- 3 (x + 2) = 1
⇒ 6x – 2 – 3x – 6 = 1
⇒ 6x – 3x – 2 – 6 = 1
⇒ 3x – 8 = 1 ⇒ 3x = 1 + 8
⇒ 3x = 9 ⇒ x = \(\frac{9}{3}\) = 3
∴ ନିର୍ଦେୟ ସମାଧାନ 3 ।

(ii) (x + 3) (x – 5) – 15 = x (x – 1)
ସମାଧାନ:
(x + 3) (x – 5) – 15 = x (x – 1)
⇒ x (x – 5) + 3 (x- 5)- 15 = x² – x
⇒ x² – 5x + 3x – 15- 15 = x² – x
⇒ x² – x² – 5x + 3x + x = 15 + 15
⇒ -x = 30 ⇒ x = -30
∴ ନିର୍ଦେୟ ସମାଧାନ -30 ।

(iii) 3 (x + a) – b = 2(x + b) + a
ସମାଧାନ:
3 (x + a) – b = 2 (x + b) + a
⇒ 3x + 3a – b = 2x + 2b + a
⇒ 3x – 2x = 2b + a – 3a + b
⇒ x = 2b + b + a – 3a
⇒ x = 3b – 2a
∴ ନିର୍ଦେୟ ସମାଧାନ 3b – 2a ।

(iv) (x – 5)² + 2(x – 3) – (x + 2)(x – 2) – 1
ସମାଧାନ:
(x – 5)² + 2 (x – 3) = (x + 2) (x – 2) – 1
⇒ x² – 10x + 25 + 2x- 6 = x² – 4 – 1
⇒ x² – x² – 8x = -4 – 1 – 25 + 6
⇒ -8x = -24 ⇒ 8x = 24
⇒ x = \(\frac{24}{8}\) = 3
∴ ନିର୍ଦେୟ ସମାଧାନ 3 ।

(v) (x – 3)² = 2x (x – 1) – x (x + 3) – 2
ସମାଧାନ:
(x – 3)² = 2x (x – 1) – x (x + 3) – 2
⇒ x² – 6x + 9 = 2x² – 2x – x² – 3x – 2
⇒ x² + x² – 2x² – 6x + 2x + 3x = -2 – 9
⇒ -x = -11 ⇒ x = 11
∴ ନିର୍ଦେୟ ସମାଧାନ 11 ।

(vi) (x + 2)² = 3x (x + 1) – 2x (x – 1)
ସମାଧାନ:
(x + 2)² = 3x (x + 1) – 2x (x – 1)
⇒ x² + 4x + 4 = 3x² + 3x – 2x² + 2x
⇒ x² – 3x² + 2x² + 4x – 3x – 2x + 4 = 0
⇒ 3x² – 3x² + 4x – 5x = -4
⇒ – x = -4 ⇒ x = 4
∴ ନିର୍ଦେୟ ସମାଧାନ 4 ।

Question 4.
ସମାଧାନ କର :

(i) x – \(\frac{2 x-1}{3}=\frac{x-2}{4}+\frac{1}{3}\)
ସମାଧାନ:

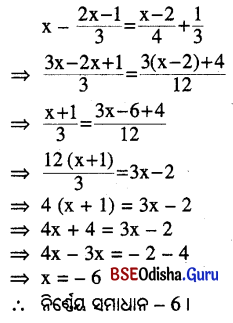
(ii) \(\frac{2-3 x}{4}+\frac{3-2 x}{5}\) = 2 – x
ସମାଧାନ:

(iii) \(\frac{3 x}{4}-\frac{5 x}{6}+2=\frac{x}{12}\)
ସମାଧାନ:

(iv) (2x – 1) – \(\frac{5(x+3)}{6}=\frac{x+5}{2}\) – 4
ସମାଧାନ:

(v) \(\frac{x-(7-8 x)}{9 x-(3+4 x)}=\frac{2}{3}\)
ସମାଧାନ:

(vi) \(\frac{x}{5}+\frac{x}{2}\) = 7
ସମାଧାନ:

Question 5.
ସମାଧାନ କର :

(i) \(\frac{1}{x+1}+\frac{1}{x+4}=\frac{2}{x+3}\)
ସମାଧାନ:

(ii) \(\frac{2}{x}+\frac{1}{2 x}-\frac{5}{x+2}\) = 0
ସମାଧାନ:

(iii) \(\frac{2}{x+1}-\frac{3}{2 x+2}=\frac{1}{2 x+3}\)
ସମାଧାନ:

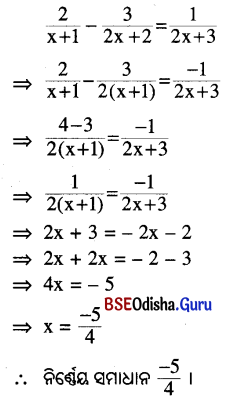
(iv) \(\frac{6}{2 x+3}+\frac{4}{x-2}=\frac{7}{x+6}\)
ସମାଧାନ:

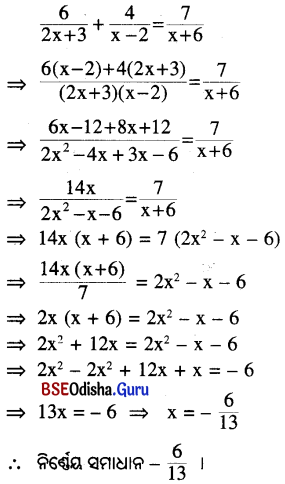
(v) \(\frac{2}{x+1}-\frac{6}{2 x-1}+\frac{3}{3 x+2}\) = 0
ସମାଧାନ:

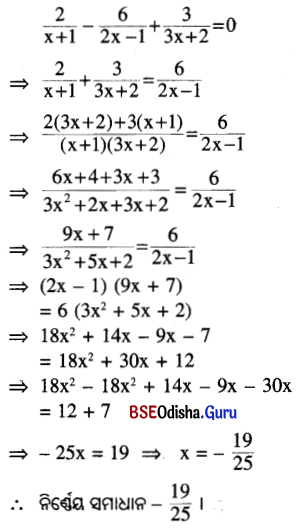
(vi) \(\frac{2}{2 x-3}+\frac{5}{(2 x-3)^2}=\frac{3}{3 x-2}\)
ସମାଧାନ: