BSE Odisha 9th Class Maths Solutions Algebra Chapter 4 ବୀଜଗାଣିତିକ ସମୀକରଣ Ex 4(c)

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 4 ବୀଜଗାଣିତିକ ସମୀକରଣ Ex 4(c) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 4 ବୀଜଗାଣିତିକ ସମୀକରଣ Ex 4(c)

Question 1.
ଦୁଇଗୋଟି କ୍ରମିକ ଗଣନ ସଂଖ୍ୟାର ବର୍ଗର ସମଷ୍ଟି 221 ହେଲେ ସଂଖ୍ୟାଦ୍ୱୟ ସ୍ଥିର କର ।
ସମାଧାନ:
ମନେକର କ୍ରମିକ ଗଣନ ସଂଖ୍ୟା ଦ୍ୱୟ x ଓ x + 1 ।
ପ୍ରଶାନୁସାରେ x² + (x + 1)² = 221 ⇒ x² + x² + 2x + 1 = 221
⇒ 2x² + 2x + 1 – 221 = 0 ⇒ 2x² + 2x – 220 = 0
⇒ x² + x – 110 = 0 (ଉଭୟ ପାର୍ଶ୍ଵକୁ 2 ଦ୍ବାରା ଭାଗକଲେ ।)
⇒ x² + 11x – 10x – 110 = 0 ⇒ x (x + 11) − 10 (x + 11) = 0
⇒ (x + 11) (x – 10) = 0 ⇒ x + 11 = 0 ବା x – 10 = 0
⇒ x = -11 ବା x = 10 ଏଠାରେ x = -11 (ଋଣାତ୍ମକ) । ତେଣୁ x = 10 ହେବ
ଗୋଟିଏ ଗଣନ ସଂଖ୍ୟା 10 ହେଲେ ଅନ୍ୟଟି = 10 + 1 = 11
∴ କ୍ରମିକ ସଂଖ୍ୟାଦ୍ଵୟ 10 ଏବଂ 11 ।

Question 2.
କୌଣସି ସଂଖ୍ୟା ତାହାର ବର୍ଗ ସହିତ ସମାନ ହେଲେ ସଂଖ୍ୟାଟି ସ୍ଥିର କର ।
ସମାଧାନ:
ମନେକର ସଂଖ୍ୟାଟି x
ପ୍ରଶ୍ନନୁସାରେ x² = x ⇒ x² – x = 0 ⇒ x(x – 1) = 0
⇒ x = 0 ବା x – 1 = 0 ⇒ x = 0 ବା 1
∴ ସଂଖ୍ୟାଟି 0 ବା 1

Question 3.
51 କୁ ଏପରି ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କର ଯେପରି ଭାଗ ଦ୍ବୟର ଗୁଣଫଳ 378 ହେବ ।
ସମାଧାନ:
ସମାଧାନ ମନେକର ଗୋଟିଏ ସଂଖ୍ୟା = x ଓ ଅନ୍ୟ ସଂଖ୍ୟାଟି = 51 – x
ପ୍ରଶ୍ନନୁସାରେ, x (51 – x) = 378 = 0 ⇒ 51 – x² = 378 ⇒ x² – 51x + 378 = 0
⇒ x² – 42x – 9x + 378 = 0 ⇒ x (x – 42) – 9(x – 42) = 0
⇒ (x – 42)(x – 9) = 0 ⇒ x – 42 = 0 ବା x – 9 = 0
⇒ x = 42 ବା x = 9
ଯଦି x = 42 ହୁଏ ତେବେ ଅନ୍ୟ ସଂଖ୍ୟାଟି 9 । ସେହିପରି ଯଦି x = 9 ହୁଏ, ତେବେ ଅନ୍ୟ ସଂଖ୍ୟାଟି 42 ।
∴ ସଂଖ୍ୟାଦ୍ଵୟ 42 ଓ 9 1

Question 4.
କୌଣସି ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜର କର୍ଣ୍ଣ ଏହାର କ୍ଷୁଦ୍ରତମ ବାହୁର ଦୈର୍ଘ୍ୟର ଦୁଇଗୁଣରୁ 1 ସେ.ମି. କମ୍ ଏବଂ ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ କ୍ଷୁଦ୍ରତମ ବାହୁର ଦୈର୍ଘ୍ୟଠାରୁ 1 ସେ.ମି. ଅଧ୍ଵ ହେଲେ, ତ୍ରିଭୁଜର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ସମକୋଣୀ ତ୍ରିଭୁଜର କ୍ଷୁଦ୍ରତମ ବାହୁର ଦୈର୍ଘ୍ୟ = x ସେ.ମି.
କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 2x – 1 ସେ.ମି. ଓ ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ = (x + 1) ସେ.ମି.
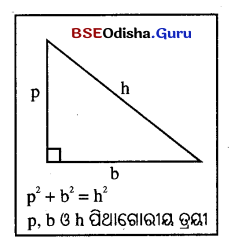ପ୍ରଶ୍ନନୁସାରେ, x² + (x + 1)² = (2x – 1)²
⇒ x² + x² + 2x + 1 = 4x² – 4x + 1
⇒ 2x² – 4x² + 2x + 4x + 1 – 1 = 0
⇒ -2x² + 6x = 0
⇒ 2x² – 6x = 0 ⇒ 2x(x – 3) = 0
⇒ x = 0 (ଏହା ଅସମ୍ଭବ) ବା x – 3 = 0 ⇒ x = 3
 କ୍ଷୁଦ୍ରତମ ବାହୁର ଦୈର୍ଘ୍ୟ = 3 ସେ.ମି.
ଅନ୍ୟ ବାହୁର ଦୈର୍ଘ୍ୟ = x + 1 = 3 + 1 = 4 ସେ.ମି.
କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 2x – 1 = 2 × 3 – 1 = 6 – 1 = 5 ସେ.ମି.
∴ ତ୍ରିଭୁଜର ତିନି ବାହୁର ଦୈର୍ଘ୍ୟ 3 ସେ.ମି., 4 ସେ.ମି. ଓ 5 ସେ.ମି. ।

Question 5.
କୌଣସି ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜର ସମକୋଣ ସଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 5x ସେ.ମି. ଓ 3x – 1 ସେ.ମି. ଏବଂ ଏହାର କ୍ଷେତ୍ରଫଳ 60 ବର୍ଗ ସେ.ମି. ହେଲେ, ତ୍ରିଭୁଜର ବାହୁ ତ୍ରୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
କୌଣସି ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜର ସମକୋଣ ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟ 5x ସେ.ମି. ଓ 3x – 1 ସେ.ମି. ।
କ୍ଷେତ୍ରଫଳ = 60 ବର୍ଗ ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{1}{2}\) (5x) (3x – 1) = 60 ⇒ 15x² – 5x = 120
⇒ 15x² – 5x – 120 = 0 ⇒ 5(3x² – x – 24) = 0
⇒ 3x² – x – 24 = 0 ⇒ 3x² – 9x + 8x – 24 = 0
⇒ 3x (x – 3) + 8 (x – 3) = 0 ⇒ (x – 3)(3x + 8) = 0
⇒ x – 3 = 0 ବା 3x + 8 = 0 ⇒ x = 3 ବା x = \(\frac{-8}{3}\) (ଏହା ଅସମ୍ଭବ)
ସମକୋଣ ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟ 5x = 5 × 3 = 15 ସେ.ମି. ଏବଂ 3x – 1 = 3 × 3 – 1 = 8 ସେ.ମି. ।
କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ \(\sqrt{15^2+8^2}=\sqrt{225+64}=\sqrt{289}\) = 17 ସେ.ମି. ।
∴ ସମକୋଣୀ ତ୍ରିଭୁଜର ବାହୁ ତ୍ରୟର ଦୈର୍ଘ୍ୟ 8 ସେ.ମି., 15 ସେ.ମି. ଓ 17 ସେ.ମି. ।

Question 6.
କୌଣସି ଏକ ସଂଖ୍ୟା ଓ ଏହାର ବ୍ୟତ୍‌କ୍ରମ ସଂଖ୍ୟା (Reciprocal)ର ସମଷ୍ଟି \(\frac{17}{4}\) ହେଲେ, ସଂଖ୍ୟାଟି ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ସଂଖ୍ୟାଟି x ଓ ଏହାର ବ୍ୟୁତ୍‌କ୍ରମ \(\frac{1}{x}\)
ପ୍ରଶ୍ନନୁସାରେ, x + \(\frac{1}{x}\) = \(\frac{17}{4}\) ⇒ \(\frac{x^2+1}{x}=\frac{17}{4}\)
⇒ 4x² + 4 = 17x ⇒ 4x² – 17x + 4 = 0
⇒ 4x² – 16x – x + 4 = 0 ⇒ 4x (x – 4) – 1 (x + 4) = 0
⇒ (x – 4) (4x – 1) = 0 ⇒ x – 4 = 0 ବା 4x – 1 = 0
⇒ x = 491 x = \(\frac{1}{4}\)
ଯଦି x = 4 ହୁଏ, ତେବେ ଏହାର ବ୍ୟତ୍‌କ୍ରମ \(\frac{1}{4}\) ହେବ ।
ପୁନଶ୍ଚ ଯଦି x = \(\frac{1}{4}\) ହୁଏ, ତେବେ ଏହାର ବ୍ୟତ୍‌କ୍ରମ 4 ହେବ ।
∴ ସଂଖ୍ୟାଟି 4 କିମ୍ବା \(\frac{1}{4}\) ।

Question 7.
କୌଣସି ଏକ ଆୟତାକାର କ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ ପ୍ରସ୍ଥ ଅପେକ୍ଷା ୫ ମି. ଅଧ୍ବକ । ଯଦି ଉକ୍ତ ଆୟତାକାର କ୍ଷେତ୍ରଟିର କ୍ଷେତ୍ରଫଳ 308 ବର୍ଗ ମି. ହୁଏ, ତେବେ ଏହାର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଆୟତାକାର କ୍ଷେତ୍ରର ପ୍ରସ୍ଥ = x ମି. ଓ ଦୈର୍ଘ୍ୟ = (x + 8) ମି.
ଆୟତାକାର କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (x + 8) x ବର୍ଗ ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, (x + 8) x = 308 = x² + 8x – 308 = 0
⇒ x² + 22x – 14x – 308 = 0 ⇒ x (x + 22) – 14 (x + 22) = 0
⇒ (x – 14) (x + 22) = 0 ⇒ x – 14 = 0 କିମ୍ବା x + 22 = 0
⇒ x = 14 କିମ୍ବା x = -22 (ଏହା ଅସମ୍ଭବ)
ଆୟତାକାର କ୍ଷେତ୍ରର ପ୍ରସ୍ଥ = 16 ମି. ଓ ଦୈର୍ଘ୍ୟ = x + 8 = 14 + 8 = 22 ମିଟର ।
∴ ଆୟତାକାର କ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ 22 ମିଟର ଓ ପ୍ରସ୍ଥ 14 ମିଟର ।

Question 8.
ଗୋଟିଏ ଶ୍ରେଣୀର ପିଲାମାନେ ଭ୍ରମଣରେ ଯିବା ପାଇଁ 3600 ଟଙ୍କା ଭଡ଼ାରେ ଏକ ବସ୍ ବରାଦ କଲେ । କିନ୍ତୁ ଶେଷବେଳକୁ ସେମାନଙ୍କ ମଧ୍ୟରୁ 3 ଜଣ ପିଲା ଓହରି ଯିବାରୁ ପ୍ରତ୍ୟେକଙ୍କୁ ଆଉ ଚାଳିଶ ଟଙ୍କା ଲେଖାଏଁ ଅଧିକ ଦେବାକୁ ପଡ଼ିଲା । ପ୍ରଥମରୁ କେତେ ପିଲା ଯିବା ପାଇଁ ମନସ୍ଥ କରିଥିଲେ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ପ୍ରଥମରୁ x ଜଣ ପିଲା ଭ୍ରମଣକୁ ଯିବାପାଇଁ ମନସ୍ଥ କରିଥିଲେ ।
x ଜଣ ପିଲା ଟଙ୍କା ପାଇଁ 3600 ବସ୍ ଭଡ଼ା ପଡ଼ିଥିଲେ
ପ୍ରତି ଜଣକୁ ଦେବାକୁ ପଡ଼ିଥା’ନ୍ତା = \(\frac{3600}{x-3}\) ଟଙ୍କା
3 ଜଣ ପିଲା ଓହରିଯିବାରୁ ଭ୍ରମଣପାଇଁ ଗଲେ = (x – 3) ଜଣ
(x – 3) ଜଣ ପିଲା ପାଇଁ 3600 ଟଙ୍କା ବସ୍‌ଭଡ଼ା ପଡ଼ିଲେ ପ୍ରତ୍ୟେକକୁ ଭଡ଼ା ଦେବାକୁ ପଡ଼ିବ = \(\frac{3600}{x-3}\) ଟଙ୍କା
ପ୍ରଶ୍ନ।ନୁସାରେ, \(\frac{3600}{x-3}-\frac{3600}{x}\) = 40 ⇒ 3600 (\(\frac{1}{x-3}-\frac{1}{x}\)) = 40
⇒ \(\frac{1}{x-3}-\frac{1}{x}=\frac{40}{3600} \Rightarrow \frac{x-x+3}{x(x-3)}=\frac{1}{90}\)
⇒ x (x – 3) = 3 × 90 ⇒ x² – 3x – 270 = 0
⇒ x² – 18x + 15x – 270 = 0 ⇒ x (x – 18) + 15 (x – 18) = 0
⇒ (x – 18) (x + 15) = 0 ⇒ x – 18 = 0 ବା x + 15 = 0
⇒ x = 18 ବା x = -15 (ଅସମୃବ)
∴ ପ୍ରଥମରୁ 18 ଜଣ ପିଲା ଭ୍ରମଣ ପାଇଁ ମନସ୍ଥ କରିଥିଲେ ।

Question 9.
ତିନିଗୋଟି କ୍ରମିକ ଗଣନ ସଂଖ୍ୟାର ବର୍ଗର ସମଷ୍ଟି 110 ହେଲେ ସଂଖ୍ୟା ତିନୋଟି ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ତିନୋଟି କ୍ରମିକ ଗଣନ ସଂଖ୍ୟା x, x + 1 ଓ (x + 2 )
ପ୍ରଶ୍ନ।ନୁସାରେ, x² + (x + 1)² + (x + 2)² = 110
⇒ x² + x² + 2x + 1 + x² + 4x + 4 = 110
⇒ 3x² + 6x + 5 = 110 ⇒ 3x² + 6x + 5 – 110 = 0
⇒ 3x² + 6x – 105 = 0 ⇒ 3 (x² + 2x – 35) = 0
⇒ x² + 2x – 35 = 0 (ଉଭୟ ପାର୍ଶ୍ଵକୁ 3 ଦ୍ବାରା ଭାଗକଲେ ।)
⇒ x² + 7x – 5x – 35 = 0 ⇒ x (x + 7) – 5 (x + 7) = 0
⇒ (x + 7) (x – 5) = 0 ⇒ x + 7 = 0 ବା x – 5 = 0
⇒ x = -7 (ଏହା ଅସମ୍ଭବ) ବା x = 5
⇒ x + 1 = 5 + 1 = 6, x + 2 = 5 + 2 = 7
∴ ତିନିଗୋଟି କ୍ରମିକ ଗଣନ ସଂଖ୍ୟା 5, 6 ଓ 7 1

Question 10.
ଦୁଇଗୋଟି କ୍ରମିକ ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ବର୍ଗର ସମଷ୍ଟି 290 ହେଲେ ସଂଖ୍ୟା ଦୁଇଟି ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର କ୍ରମିକ ଅଯୁଗ୍ମ ସଂଖ୍ୟାଦ୍ଵୟ x ଓ x + 2 ।
ପ୍ରଶ୍ନ।ନୁସାରେ, x² + (x + 2)² = 290 ⇒ x² + x² + 4x + 4 – 290 = 0
⇒ 2x² + 4x – 286 = 0 ⇒ 2(x² + 2x – 143) = 0
⇒ x² + 2x – 143 = 0
⇒ x² + 13x – 11x – 143 = 0 ⇒ x (x + 13) – 11 (x + 13) = 0
⇒ (x + 13) (x – 11) = 0 ⇒ x + 13 = 0 ବା x – 11 = 0
⇒ x = -13 ବା x = 11
⇒ x = -13 ହେଲେ x + 2 = -13 + 2 = -11
⇒ x= 11 ହେଲେ x + 2 = 11 + 2 = 13
∴ କ୍ରମିକ ଅଯୁଗ୍ମ ସଂଖ୍ୟାଦ୍ୱୟ – 13 ଓ – 11 ବା 11 ଓ 13 

Question 11.
ଏକ ଆୟତ କ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ, ପ୍ରସ୍ଥ ଅପେକ୍ଷା 2 ମିଟର ଅଧୂକ । ଯଦି କ୍ଷେତ୍ରଟିର କ୍ଷେତ୍ରଫଳ 48 ବର୍ଗ ମିଟର ହୁଏ, ତେବେ ଆୟତକ୍ଷେତ୍ରର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଆୟତକ୍ଷେତ୍ରର ପ୍ରସ୍ଥ = x ମିଟର ଓ ଦୈର୍ଘ୍ୟ = (x + 2) ମିଟର ।
ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (x + 2) x ବର୍ଗ ମିଟର ।
ପ୍ରଶ୍ନ।ନୁସାରେ, x (x + 2) = 48 ⇒ x² + 2x = 48
⇒ x² + 2x – 48 = 0 ⇒ x² + 8x – 6x – 48 = 0
⇒ x (x + 8)- 6 (x + 8) = 0 ⇒ (x – 6) (x + 8) = 0
⇒ x – 6 = 0 ବା x + 8 = 0 ⇒ x = 6 ବା x = -8 (ଏହା ଅସମ୍ଭବ)
ପ୍ରସ୍ଥ = 6 ସେ.ମି., ଦୈର୍ଘ୍ୟ = x + 2 = 6 + 2 = 8 ସେ.ମି. ।
ଆୟତକ୍ଷେତ୍ରର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 8 ସେ.ମି. ଓ 6 ସେ.ମି. ।

Question 12.
ଏକ ମୋଟର ଲଞ୍ଚ ନଦୀ ସ୍ରୋତର ଅନୁକୂଳରେ 36 କି.ମି. ଯାତ୍ରା କରି ଯାତ୍ରା ଆରମ୍ଭ ସ୍ଥାନକୁ ଫେରି ଆସିବାକୁ ସମୁଦାୟ 8 ଘଣ୍ଟା ସମୟ ନେଲା । ଯଦି ସ୍ରୋତର ଘଣ୍ଟା ପ୍ରତି ବେଗ 6 କି.ମି. ହୁଏ, ତେବେ ସ୍ଥିର ଜଳରେ ଲଞ୍ଚଟିର ଘଣ୍ଟାପ୍ରତି ବେଗ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ମୋଟର ଲଞ୍ଚର ସ୍ଥିର ଜଳରେ ଘଣ୍ଟା ପ୍ରତି ବେଗ = x କି.ମି. ।
ସ୍ରୋତର ଘଣ୍ଟା ପ୍ରତି ବେଗ = 6 କି.ମି. ।
ସ୍ରୋତର ଅନୁକୂଳରେ ଲଞ୍ଚଟି 1 ଘଣ୍ଟାରେ ଯିବ = (x + 6) କି.ମି. ।
ସ୍ରୋତର ପ୍ରତିକୂଳରେ ଲଞ୍ଚଟି 1 ଘଣ୍ଟାରେ ଯିବ = (x – 6) କି.ମି. ।
ସ୍ରୋତର ଅନୁକୂଳରେ ଲଞ୍ଚଟିକୁ 36 କି.ମି. ଯିବାକୁ ସମୟ ଲାଗିବ = \(\frac{36}{x+6}\) ଘଣ୍ଟା
ସ୍ରୋତର ପ୍ରତିକୂଳରେ ଲଞ୍ଚଟିକୁ 36 କି.ମି. ଯିବାକୁ ସମୟ ଲାଗିବ = \(\frac{36}{x=6}\) ଘଣ୍ଟା
ପ୍ରଶ୍ନ।ନୁସାରେ, \(\frac{36}{x+6}+\frac{36}{x-6}\) = 8 ⇒ 36(\(\frac{1}{x+6}+\frac{1}{x-6}\)) = 8
⇒ \(\frac{x-6+x+6}{(x+6)(x-6)}=\frac{8}{36}\) ⇒ \(\frac{2 x}{x^2-36}=\frac{8}{36}\)
⇒ \(\frac{x}{x^2-36}=\frac{4}{36}=\frac{1}{9}\) ⇒ x² – 36 = 96
⇒ x² – 9x – 36 = 0 ⇒ x² – 12x + 3x – 36 = 0
⇒ x (x – 12) + 3 (x – 12) = 0 ⇒ (x – 12) (x + 3) = 0
⇒ x – 12 = 0 ବା x + 3 = 0 ⇒ x = 12 ବା x = -3 (ଅସମୃବ)
∴ ମୋଟର ଲଞ୍ଚର ଘଣ୍ଟାପ୍ରତି ବେଗ 12 କି.ମି. ।

Question 13.
ଦୁଇଗୋଟି ବର୍ଗାକାର କ୍ଷେତ୍ର ମଧ୍ୟରୁ ଗୋଟିକର ବାହୁର ଦୈର୍ଘ୍ୟ ଅପରଟିର ଦୁଇ ଗୁଣରୁ ଏକ ମିଟର କମ୍ । ଯଦି କ୍ଷେତ୍ରଦ୍ଵୟର କ୍ଷେତ୍ରଫଳମାନଙ୍କ ଅନ୍ତର 56 ବର୍ଗ ମିଟର ହୁଏ, ତେବେ ଦୁଇଟି ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = x ମିଟର ।
 ଅନ୍ୟ ଏକ ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = (2x – 1) ମିଟର ।
କ୍ଷେତ୍ରଦ୍ୱୟର କ୍ଷେତ୍ରଫଳ ଯଥାକ୍ରମେ x² ବର୍ଗ ମି. ଏବଂ (2x – 1)² ବର୍ଗ ମି.
ପ୍ରଶ୍ନ।ନୁସାରେ, (2x- 1)² – x² = ବର୍ଗ ମି. ⇒ 4x² – 4x + 1 – x² = 56
⇒ 3x² – 4x + 1 – 56 = 0 ⇒ 3x² – 4x – 55 = 0
⇒ 3x² – 15x + 11x – 55 = 0 ⇒ 3x (x – 5) + 11 (x – 5) = 0
⇒ (x – 5)(3x + 11) = 0 ⇒ x – 5 = 0 ବା 3x + 11 =0
⇒ x = 5 ବା 3x= -11 ⇒ x = 5 ବା x = \(\frac{-11}{3}\)
ଏଠାରେ x = \(\frac{-11}{3}\) (ଅସମୃବ)
x = 5 ମି. ହେଲେ 2x – 1 = 2 × 5 – 1 = 10 – 1=9 ମି.
ବର୍ଗକ୍ଷେତ୍ରଦ୍ଵୟର ବାହୁର ଦୈର୍ଘ୍ୟ 5 ମି. ଓ 9 ମି. ।

Question 14.
ଦୁଇଟି ଗଣନ ସଂଖ୍ୟା ମଧ୍ୟରୁ ଗୋଟିଏ ଅପରଟିର ତିନି ଗୁଣରୁ ଦୁଇ କମ୍ । ଯଦି ସଂଖ୍ୟା)ଦ୍ୱୟର ବର୍ଗର ଅନ୍ତର 312 ହୁଏ, ତେବେ ସଂଖ୍ୟାଦ୍ଵୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଗୋଟିଏ ଗଣନ ସଂଖ୍ୟା = x, ପ୍ରଶ୍ନନୁସାରେ ଅନ୍ୟ ଗଣନ ସଂଖ୍ୟା = 3x – 2 
ପ୍ରଶ୍ନ।ନୁସାରେ, (3x- 2)² – x² = 312 ⇒ 9x² – 12x + 4 – x² = 312
⇒ 8x² – 12x + 4 – 312 = 0 ⇒ 8x² – 12x – 308 = 0
⇒ 4 (2x² – 3x – 77) = 0
⇒ 2x² – 3x – 77 = 0 (ଉଭୟ ପାର୍ଶ୍ଵକୁ 4 ଦ୍ବାରା ଭାଗକଲେ ।)
⇒ 2x² – 14x + 11x – 77 = 0 ⇒ 2x(x – 7) + 11(x – 7) = 0
⇒ (x – 7)(2x + 11) = 0 ⇒ x – 7 = 0 ବା 2x + 11 =0
ଯଦି x – 7 = 0 ହୁଏ, ତେବେ x = 7
ଯଦି 2x + 11 = 0 ହୁଏ, ତେବେ 2x = -11 ⇒ x = \(\frac{-11}{3}\) (ଏହା ଅସମ୍ଭବ)
x = 7 ହେଲେ 3x – 2 = 3 × 7 – 2 = 21 – 2 = 19
∴ ଗଣନ ସଂଖ୍ୟାଦ୍ଵୟ 7 ଓ 19 ।

Question 15.
ଦୁଇଟି ଷ୍ଟେସନ୍ Á ଓ B ମଧ୍ୟରେ ଦୂରତା 192 କି.ମି. । ଏକ ଦ୍ରୁତଗାମୀ ଟ୍ରେନ୍ A ରୁ Bକୁ ଯିବାକୁ ଯେତିକି ସମୟ ନିଏ ଏକ ପାସେଞ୍ଜର ଟ୍ରେନ୍ ତା’ଠାରୁ ଦୁଇଘଣ୍ଟା ଅଧିକ ସମୟ ନିଏ । ଯଦି ପାସେଞ୍ଜର ଟ୍ରେନ୍‌ର ଘଣ୍ଟା ପ୍ରତି ହାରାହାରି ବେଗ ଦୃତଗାମୀ ଟ୍ରେନ୍‌ର ଘଣ୍ଟା ପ୍ରତି ହାରାହାରି ବେଗ ଠାରୁ 16 କି.ମି. କମ୍ ହୁଏ, ତେବେ ଟ୍ରେନ୍‌ଦ୍ଵୟର ହାରାହାରି ଘଣ୍ଟା ପ୍ରତି ବେଗ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
 A ଓ B ଦୁଇଟି ଷ୍ଟେସନ ମଧ୍ୟରେ ଦୂରତା = 192 କି.ମି.
ମନେକର ଦ୍ରୁତଗାମୀ ଟ୍ରେନ୍‌ର ଘଣ୍ଟା ପ୍ରତି ହାରାହାରି ବେଗ = x କି.ମି.
ପାସେଞ୍ଜର ଟ୍ରେନ୍‌ର ଘଣ୍ଟାପ୍ରତି ହାରାହାରି ବେଗ = (x – 16) କି.ମି. ।
192 କି.ମି. ବାଟ ଯିବାକୁ ଦ୍ରୁତଗାମୀ ଟ୍ରେନ୍‌କୁ ସମୟ ଲାଗିବ = \(\frac{192}{x}\) ଘଣ୍ଟା (∴ ସମୟ =\(\frac{ଦୂରତା}{ବେଗ}\)
192 କି.ମି. ଯିବାକୁ ପାସେଞ୍ଜର ଟ୍ରେନ୍‌କୁ ସମୟ ଲାଗିବ = \(\frac{192}{x-16}\) ଘଣ୍ଟା
ପ୍ରଶ୍ନ।ନୁସାରେ, \(\frac{192}{x-16}-\frac{192}{x}\) = 2 ⇒ 192(\(\frac{1}{x-16}-\frac{1}{x}\)) = 2 ⇒ \(\frac{1}{x-16}-\frac{1}{x}=\frac{2}{192}\)
⇒ \(\frac{x-x+16}{x(x-16)}=\frac{1}{96}\) ⇒ x(x – 16) = 16 × 96
⇒ x² – 16x – 1536 = 0 ⇒ x² – 48x + 32x – 1536 = 0
⇒ x(x – 48) + 32(x – 48) = 0 ⇒ (x – 48) (x + 32) = 0
⇒ x – 48 = 0 କିମୃ। x + 32 = 0 ⇒ x = 48 କିମୃ। x = -32 (ଏହା ଅସମ୍ଭବ)
∴ ଦ୍ରୁତଗାମୀ ଟ୍ରେନ୍‌ର ଘଣ୍ଟା ପ୍ରତି ହାରାହାରି ବେଗ = 48 କି.ମି. ।
ପାସେଞ୍ଜର ଟ୍ରେନ୍‌ର ଘଣ୍ଟା ପ୍ରତି ହାରାହାରି ବେଗ = x – 16 = 48 – 16 = 32 କି.ମି. ।

Question 16.
ଗୋଟିଏ ନୌକାର ଘଣ୍ଟା ପ୍ରତି ବେଗ ସ୍ଥିର ଜଳରେ 11 କି.ମି. । ଏହା ସ୍ରୋତର ପ୍ରତିକୂଳରେ 12 କି.ମି. ଗତିକରି ପୁନଶ୍ଚ ଅନୁକୂଳରେ ଫେରିଆସିବାକୁ ମୋଟ 2 ଘଣ୍ଟା 45 ମିନିଟ୍ ସମୟ ନେଲା ତେବେ ସ୍ରୋତର ଘଣ୍ଟାପ୍ରତି ବେଗ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ସ୍ରୋତର ବେଗ = x କି.ମି.|ଘଣ୍ଟା । ଦତ୍ତ ଅଛି ନୌକାର ବେଗ = 11 କି.ମି. /ଘଣ୍ଟା ।
∴ ସ୍ରୋତର ଅନୁକୂଳରେ ନୌକାର ବେଗ (11 + x) କି.ମି. /ଘଣ୍ଟା
ଏବଂ ପ୍ରତିକୂଳରେ ନୌକାର ବେଗ = (11 – x) କି.ମି. /ଘଣ୍ଟା 
ସ୍ରୋତର ଅନୁକୂଳରେ 12 କି.ମି. ଅତିକ୍ରମ କରିବା ପାଇଁ ସମୟ ଲାଗିବ = \(\frac{12}{11+x}\) ଘଣ୍ଟା
ଏବଂ ସ୍ରୋତର ପ୍ରତିକୂଳରେ 12 କି.ମି. ଅତିକ୍ରମ କରିବା ପାଇଁ ସମୟ ଲାଗିବ = \(\frac{12}{11-x}\) ଘଣ୍ଟା
ପ୍ରଶ୍ନ।ନୁସାରେ, \(\frac{12}{11+x}+\frac{12}{11-x}\) = 2 \(\frac{45}{60}\) ବା 2 \(\frac{3}{4}\) ⇒ \(\frac{132-12 x+132+12 x}{(11+x)(11-x)}=\frac{11}{4}\)
⇒ \(\frac{264}{121-x^2}=\frac{11}{4}\) ⇒ 1056 = 1331 – 11x²
⇒ 11x² = 1331 – 1056 = 275 ⇒ x² = \(\frac{275}{11}\) ⇒ x = √25 = 5
∴ ସ୍ରୋତର ଘଣ୍ଟା ପ୍ରତି ବେଗ 5 କି.ମି. ।

Question 17.
ଗୋଟିଏ ଗାଈଗୋଠର ଏକ ଚତୁର୍ଥାଂଶ ଦୃଷ୍ଟିଗୋଚର ହେଉଥିଲେ । ଗୋଠରେ ଥ‌ିବା ଗାଈ ସଂଖ୍ୟାର ବର୍ଗମୂଳର ଦୁଇଗୁଣ ସଂଖ୍ୟକ ଗାଈ ପାହାଡ଼ର ପାଦଦେଶରେ ଚରୁଥିଲେ ଏବଂ ଅବଶିଷ୍ଟ 15 ଟି ଗାଈ ନଦୀକୂଳରେ ଚରୁଥିଲେ । ତେବେ ଗୋଠରେ କେତୋଟି ଗାଈ ଥିଲେ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଗାଈ ଗୋଠରେ x²ଟି ଗାଈ ଥିଲେ । ଦୃଷ୍ଟିଗୋଚର ହେଉଥ‌ିବା ଗାଈ ସଂଖ୍ୟା = \(\frac{x^2}{4}\)
ପାହାଡ଼ର ପାଦ ଦେଶରେ ବୁଲୁଥ‌ିବା ଗାଈ ସଂଖ୍ୟା = 2x  ନଦୀକୂଳରେ ଚରୁଥିବା ଗାଈ ସଂଖ୍ୟା = 15
ପ୍ରଶ୍ନ।ନୁସାରେ, x² = \(\frac{x^2}{4}\) + 2x + 15 ⇒ x² = \(\frac{x^2+8 x+60}{4}\)
⇒ 4x² – x² – 8x- 60 = 0 ⇒ 3x² – 8x – 60 = 0
⇒ 3x² – 18x + 10x – 60 = 0 ⇒ 3x (x – 6) + 10 (x-  6) = 0
⇒ (x – 6) (3x + 10) = 0 ⇒ x – 6 = 0 ଘଣ୍ଟା  3x + 10 = 0
⇒ x = 6 ଘଣ୍ଟା x = \(\frac{-10}{3}\) (ଏହା ଅସମ୍ଭବ)
⇒ x² = 6² = 36
∴ ଗୋଠରେ 36ଟି ଗାଈ ଥିଲେ ।
ବିକଳ୍ପ ପ୍ରଣାଳୀ : ମନେକର ଗୋଠରେ ଥିବା ଗାଈ ସଂଖ୍ୟା = x
∴ ଦୃଷ୍ଟିଗୋଚର ହେଉଥୁବା ଗାଈ ସଂଖ୍ୟା = \(\frac{x}{4}\)
ପ୍ରଶ୍ନନୁସାରେ, x= \(\frac{x}{4}\) + 2√x + 15 ⇒ \(\frac{3x}{4}\) – 15=2√x
⇒ 3x – 60 = 8√x ⇒ 9x² + 3600 – 360x = 64x
⇒ 9x² – 424x + 3600 = 0 ⇒ (x – 36) (9x – 100) = 0 ⇒ x = 36
∴ ଗୋଠରେ ଥ‌ିବା ଗାଈ ସଂଖ୍ୟା 36 ।