Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 2 ତ୍ରିଭୁଜମାନଙ୍କ ସର୍ବସମତା Ex 2(a) Textbook Exercise Questions and Answers.
BSE Odisha Class 9 Maths Solutions Geometry Chapter 2 ତ୍ରିଭୁଜମାନଙ୍କ ସର୍ବସମତା Ex 2(a)
Question 1.
ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
(i) Δ ABC ଓ Δ POR ସର୍ବସମ ହେବେ ଯଦି
(a) AB = PQ, AC = QR, m∠B = m∠Q
(b) AB = PQ, AC = QR, m∠A = m∠R
(c) AB = PQ, AC = PR, m∠A = m∠P
(d) AB = PQ, AC = QR, m∠A = m∠Q
ସମାଧାନ:
AB = PQ, AC = PR, m∠A = m∠P; AB = PQ, AC = QR, m∠A = m∠Q
(ii) Δ ABC ଓ Δ DEF ସର୍ବସମ ହେବେ ଯଦି
(a) m∠A = m∠D, m∠B = m∠F, AB = DF
(b) m∠A = m∠D, m∠B = m∠F, AB = DE
(c) m∠A = m∠D, m∠B = m∠F, BC = DE
(d) m∠A = m∠D, m∠B = m∠F, AC = DF
ସମାଧାନ:
m∠A = m∠D, m∠B = m∠F, AB = DF
(iii) Δ ABC ଓ Δ DE ଦୁଇଟି ସର୍ବସମ ତ୍ରିଭୁଜରେ m∠A = m∠D ଓ AB = DE ହେଲେ ନିମ୍ନସ୍ଥ କେଉଁ ସର୍ଭଟି ସତ୍ୟ ନୁହେଁ ?
(a) BC = EF
(b) m∠ACB = m∠DFE
(c) AC = DF
(d) m∠ABC = m∠DEF
ସମାଧାନ:
m∠ABC = m∠DEF
(iv) Δ ABC ଓ Δ POR ସର୍ବସମ ହେଲେ, ନିମ୍ନସ୍ଥ କେଉଁ ଉକ୍ତିଟି ସତ୍ୟ ହେବ ?
(a) AB = PQ, BC = QR, m∠C = m∠R
(b) BC = PQ, CA = QR, m∠A= m∠P
(c) AB = PQ, m∠A = m∠Q, m∠C = m∠P
(d) AB = PQ, m∠A = m∠P, m∠B = m∠Q
ସମାଧାନ:
AB = PQ, m∠A = m∠P, m∠B = m∠Q
(v) ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ର ଅନୁସାରେ m∠BAD : m∠ADB ହେଉଛି,
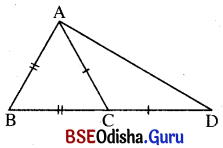
(a) 2 : 1
(b) 3 : 1
(c) 1 : 2
(d) 1 : 3
ସମାଧାନ:
3 : 1
Question 2.
ନିମ୍ନସ୍ଥ କେଉଁ କେଉଁ ସର୍ଭରେ Δ ABC ଓ Δ POR ସର୍ବସମ ହେବେ ?
(i) AB = PQ, BC = QR, m∠C = m∠R
(ii) AB = PQ, m∠A = m∠P, m∠B = m∠Q
(iii) BC = PQ, CA = QR, m∠A = m∠P
(iv) m∠P = m∠B = 90°, PQ = AB, PR = BC
(v) PQ = AB, PR = AC, A ଓ P ବିନ୍ଦୁଠାରେ ଅଙ୍କିତ ବହିଃସ୍ଥ କୌଣଦ୍ଵୟ ସର୍ବସମ ।
(vi) AB = PQ, m∠A = m∠Q, m∠C = m∠R
ସମାଧାନ:
(ii) AB = PQ, m∠A = m∠P, m∠B = m∠Q (କୋ-ବା-କୋ ସର୍ବସମତା)
(iv) m∠P = m∠B = 90°, PQ = AB, PR = BC (ବା-କୋ-ବା ସର୍ବସମତା)
(v) PQ = AB, PR = AC, A ଓ P ବିନ୍ଦୁଠାରେ ଅଙ୍କିତ ବହିଃସ୍ଥ କୌଣଦ୍ଵୟ ସର୍ବସମ ।
(vi) AB = PQ, m∠A = m∠Q, m∠C = m∠R (କୋ-ବା-କୋ ସର୍ବସମତା)
Question 3.
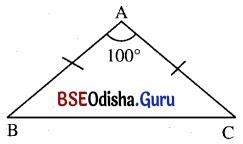
(i) ଗୋଟିଏ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ଶୀର୍ଷକୋଣର ପରିମାଣ 100° ହେଲେ, ଏହାର ପ୍ରତ୍ୟେକ ଭୂମିସଂଲଗ୍ନ କୋଣର ପରିମାଣ କେତେ ?
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ AB = AC, m∠A = 100° ।
ନିର୍ମେୟ : Δ ABC ର ପ୍ରତ୍ୟେକ ଭୂମିସଂଲଗ୍ନ କୋଣର ପରିମାଣ ।
ଡତ୍ତର : m∠A + m∠B + m∠C = 180°
⇒ 100° + m∠B + m∠B = 180° (∵ m∠B = m∠C)
⇒ 2m∠B = 80° ⇒ m∠B = 40°
∴ ΔABC ର ପ୍ରତ୍ୟେକ ଭୂମିସଂଲଗ୍ନ କୋଣଦ୍ଵୟର ପରିମାଣ 40° ।
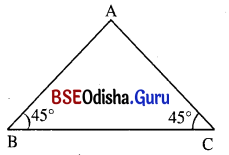
(ii) ଗୋଟିଏ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ଭୂମିସଂଲଗ୍ନ କୋଣର ପରିମାଣ 45° ହେଲେ ଏହାର ଶୀର୍ଷକୋଣର ପରିମାଣ କେତେ ?
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ AB = AC ଏବଂ m∠B = m∠C = 45°
ନିର୍ମେୟ : ∠BAC ର ପରିମାଣ ।
ଡତ୍ତର : m∠A + m∠B + m∠C = 180°
m∠A + 45° + 45° = 180° (∵ m∠B = m∠C = 45°)
m∠A = 180° – 90° = 90°
∴ ଶୀର୍ଷକୋଣର ପରିମାଣ 90° ।
Question 4.
Δ ABC ରେ AC ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ AB କୁ D ବିନ୍ଦୁରେ ଛେଦ କରୁଥିଲେ, ଦର୍ଶାଅ ଯେ AB = BD + DC ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ର ACର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ DE, AB କୁ D ବିନ୍ଦୁରେ ଛେଦକରେ,
ଅର୍ଥାତ୍ DE = E͞C ଓ D͞E ⊥ AC ।
ପ୍ରାମାଣ୍ୟ : AB = BD + DC
ଅଙ୍କନ : ED ଅଙ୍କନ କରାଯାଉ ।
ପ୍ରମାଣ : Δ ADE ଓ Δ DEC ମଧ୍ୟରେ AE = CE (ଦତ୍ତ )
m∠DEA = m∠DEC = 90° (DE ⊥ AC)
DE ସାଧାରଣ ବାହୁ ।
∴ Δ ADE = Δ CDE (ବା-କୋ-ବା ସର୍ବସମତା)
⇒ AD ≅ CD
AB = AD + BD = CD + BD (∵ AD = CD)
AB = BD + DC
(ପ୍ରମାଣିତ)
Question 5.
ଦର୍ଶାଅ ଯେ, ସମବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ କୋଣର ପରିମାଣ 60° ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ AB = AC = BC
ପ୍ରାମାଣ୍ୟ : m∠A = m∠B = m∠C = 60°
AB = AC ⇒ m∠B = m∠C
ସେହିପରି AC = BC = m∠A = m∠B
∴ m∠A = m∠B = m∠C
କିନ୍ତୁ m∠A + m∠B + m∠C = 180°
∴ m∠A = m∠B = m∠C = \(\frac{180^{\circ}}{3}\) = 60°
(ପ୍ରମାଣିତ)
Question 6.
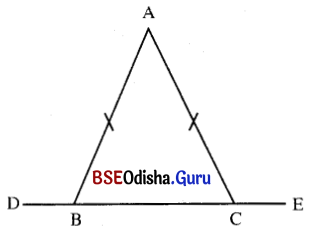
(i) ପ୍ରମାଣ କର ଯେ, କୌଣସି ତ୍ରିଭୁଜର ଦୁଇଟି ଶୀର୍ଷବିନ୍ଦୁରେ ଅଙ୍କିତ ବହିଃସ୍ଥ କୌଣଦ୍ଵୟ ସର୍ବସମ ହେଲେ, ତ୍ରିଭୁଜଟି ସମଦ୍ବିବାହୁ ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ର B ଓ C ବିନ୍ଦୁରେ ଅଙ୍କିତ ବହିଃସ୍ଥ କୌଣଦ୍ଵୟ ସର୍ବସମ ଅର୍ଥାତ୍ m∠ABD = m∠ACE ।
ପ୍ରାମାଣ୍ୟ : AABC ସମଦ୍ବିବାହୁ ଅର୍ଥାତ୍ AB = AC ।
ପ୍ରମାଣ : ∠ABD = ∠ACE
m∠ABD + m∠B= 180° = m∠ACE + ∠C (∵ ସନ୍ନିହିତ ପରିପୂରକ କୋଣ)
m∠B = m∠C (∵ ∠ABD = m∠ACE)
AB = AC ଅର୍ଥାତ୍ Δ ABC ସମଦ୍ବିବାହୁ ।
(ପ୍ରମାଣିତ)
(ii) Δ ABCରେ AB = AC ହେଲେ, B ଓ C ବିନ୍ଦୁରେ ଅଙ୍କିତ ବହିଃସ୍ଥ କୋଣଦ୍ଵୟ ସର୍ବସମ ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ AB = AC ।
B ଓ C ବିନ୍ଦୁରେ ଅଙ୍କିତ ବହିଃସ୍ଥ କୌଣଦ୍ବୟ ∠ABD ଓ ∠ACE ଅଟେ ।
ପ୍ରାମାଣ୍ୟ : m∠ABD = m∠ACE
ପ୍ରମାଣ : Δ ABC ରେ AB = AC (ଦତ୍ତ)
⇒ m∠ACB = m∠ABC
(ସମାନ ବାହୁର ବିପରୀତ କୋଣଦ୍ଵୟ ସର୍ବସମ)
⇒ m∠ABD + m∠ABC = m∠ACB + m∠ACE = 180° (∵ ସନ୍ନିହିତ ପରିପୂରକ କୋଣ)
⇒ m∠ABD = m∠ACE (∵ m∠ABC = m∠ACB)
(ପ୍ରମାଣିତ)
Question 7.
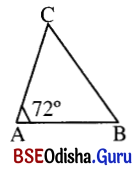
Δ ABC ରେ m∠A = 72° ଏବଂ m∠B = 2m∠C ହେଲେ ପ୍ରମାଣ କର ଯେ, ତ୍ରିଭୁଜଟି ସମଦ୍ବିବାହୁ ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ m∠A = 72° ଏବଂ m∠B = 2m∠C ।
ପ୍ରାମାଣ୍ୟ : Δ ABC ସମଦିବାହୁ ।
ପ୍ରମାଣ : Δ ABC ରେ m∠A + m∠B + m∠C = 180°
⇒ 72° + 2m∠C + m∠C = 180° (∵ m∠B = 2m∠C)
⇒ 3m∠C = 108° – 72° = 108° ⇒ m∠C = 36°
∴ m∠B = 180° – (m∠A + m∠C) = 180° – (72° + 36°)
= 180° – 108° = 72°
∴ m∠A = m∠B ⇒ BC = AC ⇒ Δ ABC ସମଦିବାହୁ ।
(ପ୍ରମାଣିତ)
Question 8.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ AB = AC ଏବଂ BO = CO, ପ୍ରମାଣ କର ଯେ, ∠ABO ≅ ∠ACO ।
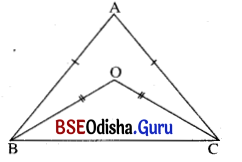
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ AB = AC ଏବଂ OB = OC ।
ପ୍ରାମାଣ୍ୟ : ∠ABO ≅ ∠ACO ।
ପ୍ରମାଣ : Δ ABC ରେ AB = AC ⇒ m∠ABC = m∠ACB … (i)
Δ OBC ରେ OB = OC (ଦତ୍ତ) ⇒ m∠OBC = m∠OCB … (ii)
(i) ଓ (ii) ରୁ m∠ABC – m∠OBC = m∠ACB – m∠OCB
⇒ m∠ABO = m∠ACO
⇒ ∠ABO = ∠ACO (ପ୍ରମାଣିତ)
ବିକଳ୍ପ ସମାଧାନ :
ଦତ୍ତ : Δ ABC ରେ AB = AC ଏବଂ BO = CO ।
ପ୍ରାମାଣ୍ୟ : ∠ABO ≅ ∠ACO ।
ଅଙ୍କନ : Δ ABO ଓ Δ ACO ମଧ୍ୟରେ
∴ AB = AC (ଦତ୍ତ) , BO = CO (ଦତ୍ତ) ଏବଂ A͞O ସାଧାରଣ ବାହୁ ।
Δ ABO ≅ Δ ACO (କୋ-ବା-କୋ ସର୍ବସମତା)
⇒ m∠ABO = m∠ACO ⇒ ∠ABO ≅ ∠ACO
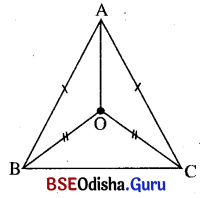
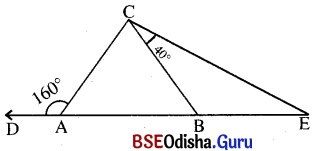
Question 9.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ AB = AC, m∠CAD = 160°, m∠BCE = 40° । ପ୍ରମାଣ କର ଯେ, BE = BC ।
ସମାଧାନ:
ଦତ୍ତ : ଦତ୍ତ ବିନ୍ଦୁରେ m∠CAD = 160° ଏବଂ m∠BCE = 40° ।
ପ୍ରାମାଣ୍ୟ : BE = BC
ପ୍ରମାଣ : Δ ABC ର ବହିଃସ୍ଥ ∠CAD ର ପରିମାଣ 160° ।
ବହିଃସ୍ଥ m∠CAD = m∠ACB + m∠ABC
m∠CAD = 2m∠ABC (m∠ACB = m∠ABC ∵ AB = AC)
⇒ 160° = 2m∠ABC ⇒ m∠ABC = 80° = m∠ACB
ପୁନଶ୍ଚ Δ CBE ରେ m∠ABC = m∠BCE + m∠CEB
⇒ 80° = 40° + m∠CEB ⇒ m∠CEB = 40°
m∠BCE = m∠CEB = 40° ⇒ BE = BC
(ପ୍ରମାଣିତ)
Question 10.
Δ ABC ରେ AB = AC ଓ A͞D ⊥ B͞C । ପ୍ରମାଣ କର ଯେ, BD = DC ଓ m∠BAD = m∠CAD ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ AB = AC ଓ A͞D ⊥ B͞C ।
ପ୍ରାମାଣ୍ୟ : BD = DC ଓ m∠BAD = m∠CAD ।
ପ୍ରମାଣ : Δ ABD ଓ Δ ADC ମଧ୍ୟରେ AB = AC (ଦତ୍ତ)
m∠ADB = m∠ADC (ସମକୋଣ) ଓ AD ସାଧାରଣ ବାହୁ ।
∴ Δ ABD ≅ Δ ADC (ସ-କ-ବା ସର୍ବସମତା)
⇒ BD = CD ଏବଂ m∠BAD = m∠CAD
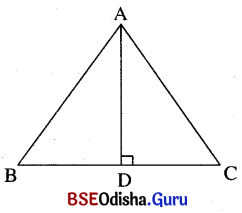(ପ୍ରମାଣିତ)
Question 11.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ AB = PQ, BC = QR ଏବଂ m∠ABX = m∠PQY । ଦର୍ଶାଅ ଯେ, Δ ABC ≅ Δ PQR ।
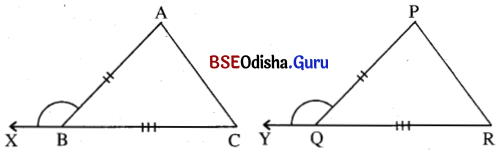
ସମାଧାନ:
ଦତ୍ତ : ଦତ୍ତ ବିନ୍ଦୁରେ AB = PQ, BC = QR ଏବଂ m∠ABX = m∠PQY ।
ପ୍ରାମାଣ୍ୟ : Δ ABC ≅ Δ PQR ।
ପ୍ରମାଣ : m∠ABX + m∠ABC = 180° ଏବଂ m∠PQY + m∠PQR = 180°
m∠ABX + m∠ABC = m∠PQY +m∠PQR
⇒ m∠ABC = m∠PQR (∵ m∠ABX = m∠PQY)
Δ ABC ଓ Δ PQR ଦ୍ଠୟରେ AB = PQ, m∠ABC = m∠PQR ଏବଂ BC = QR
∴ Δ ABC ≅ Δ PQR (ବା-କୋ-ବା ସର୍ବସମତା) (ପ୍ରମାଣିତ)
Question 12.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ A͞B ଓ C͞D ରେଖାଖଣ୍ଡଦ୍ଵୟ ପରସ୍ପରକୁ ‘O’ ବିନ୍ଦୁରେ ସମଦ୍ବିଖଣ୍ଡ କରୁଥିଲେ, ଦର୍ଶାଅ ଯେ A͞D || B͞C ।
ସମାଧାନ:
ଦତ୍ତ : A͞B ଓ C͞D ରେଖାଖଣ୍ଡ ଦ୍ବୟର ଛେଦବିନ୍ଦୁ O ।
A͞B ଓ C͞D ଦ୍ଵୟ ପରସ୍ପରକୁ ଠ ବିନ୍ଦୁରେ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି,
ଅର୍ଥାତ୍ AO = BO ଏବଂ CO = DO ।
ପ୍ରାମାଣ୍ୟ : A͞D || B͞C
ପ୍ରମାଣ : Δ AOD ଓ Δ BOC ଦ୍ଠୟରେ m∠AOD = m∠BOC
AO = BO (ଦତ୍ତ) ଏବଂ DO = CO (ଦତ୍ତ)
∴ Δ AOD = Δ BOC (ବା-କୋ-ବା ସର୍ବସମତା)
⇒ m∠DAO = m∠CBO କିନ୍ତୁ ଏ ଦ୍ବୟ ଏକାନ୍ତର କୌଣହେତୁ AD || BC
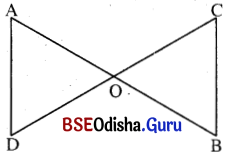(ପ୍ରମାଣିତ)
Question 13.
ABCD ଚତୁର୍ଭୁଜରେ AC କଣ୍ଠ ∠A ଓ ∠C କୁ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରୁଥୁଲେ ଦର୍ଶାଅ ଯେ, AB = AD ଏବଂ CB = CD ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଚତୁର୍ଭୁଜରେ A͞C କଣ୍ଠ, m∠BAC = m∠DAC ଓ m∠BCA = m∠DCA ।
ପ୍ରାମାଣ୍ୟ : AB = AD ଏବଂ CB = CD
ପ୍ରମାଣ : Δ ABC ଏବଂ Δ ADC ଦ୍ଠୟରେ
m∠BAC = m∠DAC (ଦତ୍ତ), A͞C ସାଧାରଣ ବାହୁ
ଏବଂ m∠BCA = m∠DCA (ଦତ୍ତ)
∴ Δ ABC = Δ ADC (କୋ-ବା-କୋ ସର୍ବସମତା)
⇒ AB = AD ଏବଂ CB = CD
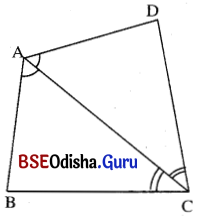(ପ୍ରମାଣିତ)
Question 14.
Δ ABC ରେ A ବିନ୍ଦୁରୁ B͞C ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ B͞C କୁ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରୁଥୁଲେ ଦର୍ଶାଅ ଯେ, ତ୍ରିଭୁଜଟି ସମଦ୍ବିବାହୁ ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ A͞D ⊥ B͞C ଓ BD = DC ।
ପ୍ରାମାଣ୍ୟ : Δ ABC ସମଦ୍ବିବାହୁ ଅର୍ଥାତ୍ AB = AC
ପ୍ରମାଣ : Δ ABD ଏବଂ Δ ADC ଦ୍ଠୟରେ BD = CD (ଦତ୍ତ)
A͞D ସାଧାରଣ ବାହୁ ଏବଂ m∠ADB = m∠ADC (ପ୍ରତ୍ୟେକ ସମକୋଣ)
∴ Δ ABD ≅ Δ ADC (ବା-କୋ-ବା ସର୍ବସମତା)
∴ AB = AC (ଅନୁରୂପ ବାହୁ) ⇒ Δ ABCଟି ସମଦ୍ବିବାହୁ ।
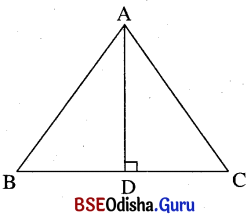(ପ୍ରମାଣିତ)
Question 15.
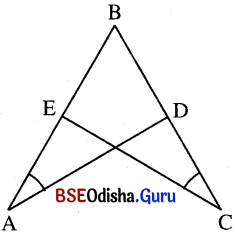
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ବୃତ୍ତ ଅଛି, m∠BAD = m∠BCE ଏବଂ AB = BC ।
ସମାଧାନ:
ଦତ୍ତ : ଦତ୍ତ ବିନ୍ଦୁରେ m∠BAD = m∠BCE ଏବଂ AB = BC ।
ପ୍ରାମାଣ୍ୟ : Δ ABD ≅ Δ CBE
ପ୍ରମାଣ : Δ ABD ଓ Δ CBE ଦ୍ଠୟରେ
m∠ABD = m∠CBE (ସାଧାରଣ)
AB = BC (ଦତ୍ତ) ଏବଂ m∠BAD = m∠BCE (ଦତ୍ତ)
Δ ABD ≅ Δ CBE (କୋ-ବା-କୋ ସର୍ବସମତା)
⇒ AD = CE
(ପ୍ରମାଣିତ)
Question 16.
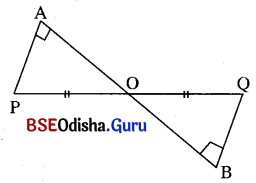
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ O, P͞Q ର ମଧ୍ୟବିନ୍ଦୁ । P͞A ଏବଂ Q͞B, A͞B ଉପରେ ଲମ୍ବ । ଦର୍ଶାଅ ଯେ A͞P = B͞Q ।
ସମାଧାନ:
ଦତ୍ତ : ଦତ୍ତ ଚିତ୍ରରେ O, P͞Q ର ମଧ୍ୟବିନ୍ଦୁ, ଅର୍ଥାତ୍ PO = OQ ।
P͞A ⊥ AB ଏବଂ Q͞B ⊥ A͞B
ପ୍ରାମାଣ୍ୟ : AP = BQ
ପ୍ରମାଣ : Δ APO ଏବଂ Δ BQO ମଧ୍ୟରେ PO = OQ (ଦତ୍ତ)
m∠PAO = m∠QBO (ସମକୋଣ) ଏବଂ m∠AOP = m∠BOQ (ପ୍ରତୀପ କୋଣ)
Δ APO ≅ Δ BQO (କୋ-ବା-କୋ ସର୍ବସମତା) ⇒ AP = BQ
(ପ୍ରମାଣିତ)
Question 17.
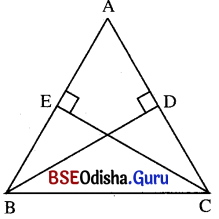
Δ ABC ରେ AB = AC । ପ୍ରମାଣ କର ଯେ, B ଓ C ବିନ୍ଦୁଠାରୁ ଏହାର ବିପରୀତ ବାହୁମାନଙ୍କ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବଦ୍ଵୟ ସର୍ବସମ ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ AB = AC,
B͞D ⊥ A͞C ଓ CE ⊥ AB ।
ପ୍ରାମାଣ୍ୟ : B͞D ≅ C͞D
ପ୍ରମାଣ : Δ ABD ଓ Δ ACE ଦ୍ଵୟରେ AB = AC (ଦତ୍ତ)
m∠BAD = m∠CAE (ସାଧାରଣ)
m∠ADB = m∠AEC = 90°
Δ ABD ≅ Δ ACE ⇒ BD ≅ CD
(ପ୍ରମାଣିତ)
Question 18.
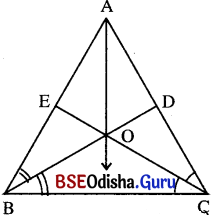
Δ ABC ରେ AB = AC । ∠B ଓ ∠C ର ସମଦ୍ବିଖଣ୍ଡକଦ୍ୱୟ ପରସ୍ପରକୁ O ବିନ୍ଦୁରେ ଛେଦ କରୁଥିଲେ, ପ୍ରମାଣ କର ଯେ
BO = CO ଏବଂ \( \overrightarrow{\mathrm{AO}}\), ∠A ର ସମଦ୍ବିଖଣ୍ଡକ ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ AB = AC । \( \overrightarrow{\mathrm{BO}}\) ଏବଂ \( \overrightarrow{\mathrm{CO}}\) ଯଥାକ୍ରମେ ∠B ଓ ∠C ର ସମର୍ଦ୍ଦିଖଣ୍ଡକ । ସମଦ୍ୱିଖଣ୍ଡକଦ୍ୱୟ AC ଓ AB କୁ ଯଥାକ୍ରମେ D ଓ E ବିନ୍ଦୁରେ ଛେଦ କରେ ।
ପ୍ରାମାଣ୍ୟ : (i) BO = CO
(ii) m∠BAO = m∠CAO;
ଅର୍ଥାତ୍ \( \overrightarrow{\mathrm{AO}}\), ∠A ର ସମଦ୍ବିଖଣ୍ଡକ ।
ପ୍ରମାଣ : m∠ABC = m∠ACB (∵ AB = AC)
⇒ \(\frac{1}{2}\)m∠ABC = \(\frac{1}{2}\)m∠ACB
⇒ m∠OBC = m∠OCB ⇒ OB = OC … (i)
ପୁନଶ୍ଚ, Δ ABO ଏବଂ Δ ACO ଦ୍ବୟରେ AB = AC (ଦତ୍ତ)
m∠ABO = m∠ACO (∵ B͞O ଏବଂ C͞O ଯଥାକ୍ରମେ ∠B ଓ ∠C ର ସମଦ୍ଵିଖଣ୍ଡକ)
ଏବଂ OB = OC ∴ Δ ABO ≅ Δ ACO
⇒ m∠BAO = m∠CAO ଅର୍ଥାତ୍ \( \overrightarrow{\mathrm{AO}}\), ∠A ର ସମଦ୍ଵିଖଣ୍ଡକ ।
(ପ୍ରମାଣିତ)
Question 19.
Δ ABC ରେ ∠B ସମକୋଣ । A͞C କର୍ପୂର ମଧ୍ୟବିନ୍ଦୁ D ହେଲେ ଦର୍ଶାଅ ଯେ BD = \(\frac{1}{2}\)AC l
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ m∠B = 90° ଏବଂ
D, A͞C ର ମଧ୍ୟବିନ୍ଦୁ ଅର୍ଥାତ୍ AD = DC l
ପ୍ରାମାଣ୍ୟ : BD = \(\frac{1}{2}\)AC
ଅଙ୍କନ : \(\overrightarrow{\mathrm{BD}}\) ଉପରେ ‘E’ ଏପରି ଏକ ବିନ୍ଦୁ ଯେପରିକି
B – D – E ଓ BD = DE l
C͞E ଅଙ୍କନ କରାଯାଉ ।
ପ୍ରମାଣ : Δ ABD ଓ Δ EDC ଦ୍ୱୟରେ AD = DC (∵ D, A͞C ର ମଧ୍ୟବିନ୍ଦୁ)
BD = DE (ଅଙ୍କନ) ଏବଂ m∠ADB = m∠EDC (ପ୍ରତୀପ)
∴ Δ ABD ≅ Δ EDC (ବା-କୋ-ବା ସର୍ବସମତା)
⇒ AB = EC ଏବଂ m∠ABD = m∠CED
କିନ୍ତୁ m∠ABD = m∠CED (ଏକାନ୍ତର)
⇒ AB || CE ⇒ m∠ABC + m∠ECB = 180° ⇒ m∠ECB = 90°
Δ ABC ଓ Δ ECB ଦ୍ୱୟରେ AB = CE (ପୂର୍ବରୁ ପ୍ରମାଣିତ)
B͞C ସାଧାରଣ ବାହୁ ଏବଂ m∠ABC = m∠ECB = 90°
∴ Δ ABC ≅ Δ ECB (ବା-କୋ-ବା ସର୍ବସମତା)
⇒ AC = BE ⇒ AC = 2BD ⇒ BD = \(\frac{1}{2}\)AC
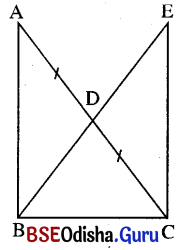
ବିକଳ୍ପ ସମାଧାନ :
ଦତ୍ତ : Δ ABCରେ ∠B ସମକୋଣ । A͞C ର ମଧ୍ୟବିନ୍ଦୁ D ଅର୍ଥାତ୍ A
ପ୍ରାମାଣ୍ୟ : BD = \(\frac{1}{2}\)AC
ଅଙ୍କନ : \(\overrightarrow{\mathrm{BD}}\) ଉପରେ E ଏକ ବିନ୍ଦୁ ନିଅ ଯେପରିକି BD = DE ହେବ ।
AE ଓ C͞E ଅଙ୍କନ କରାଯାଉ ।
ପ୍ରମାଣ : ABCD ଚତୁର୍ଭୁଜରେ AD = CD (ଦତ୍ତ) ଓ BD = DE (ଅଙ୍କନ) ।
ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
କିନ୍ତୁ m∠ABC = 90° ହେତୁ ABCD ଏକ ଆୟତଚିତ୍ର ।
BE = AC (ଆୟତଚିତ୍ରର କଣ୍ଠଦ୍ଵୟ ସର୍ବସମ)
⇒ \(\frac{1}{2}\)BE = \(\frac{1}{2}\)AC ⇒ BD = \(\frac{1}{2}\)AC
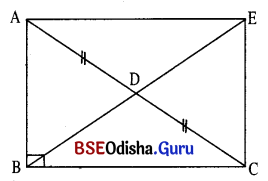(ପ୍ରମାଣିତ)
Question 20.
କୌଣସି ତ୍ରିଭୁଜର ଉଚ୍ଚତାତ୍ରୟ ସମାନ ହେଲେ, ପ୍ରମାଣ କର ଯେ ତ୍ରିଭୁଜଟି ସମବାହୁ ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ A͞D ⊥ B͞C, C͞E ⊥ A͞B, BF ⊥ AC ଏବଂ AD = CE = BF ।
ପ୍ରାମାଣ୍ୟ : AB = BC = AC
ପ୍ରମାଣ : Δ ABD ଏବଂ Δ BCE ଦ୍ଵୟରେ
m∠ABD = m∠CBE (ସାଧାରଣ)
m∠ADB = m∠CEB = 90° ଏବଂ AD = CE (ଦତ୍ତ)
∴ Δ ABD ≅ Δ BCE (କୋ-କୋ-ବା ସର୍ବସମତା) ⇒ AB = BC
ସେହିପରି ପ୍ରମାଣ କରାଯାଇ ପାରେ, Δ BFC ≅ Δ ADC ⇒ BC = AC
∴ AB = BC = AC
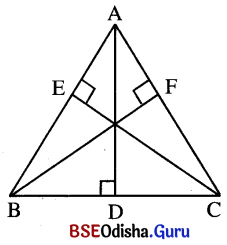(ପ୍ରମାଣିତ)
Question 21.
ତ୍ରିଭୁଜର ଗୋଟିଏ କୋଣର ସମଦ୍ବିଖଣ୍ଡକ ଏହାର ସମ୍ମୁଖୀନ ବାହୁକୁ ସମଦ୍ବିଖଣ୍ଡ କରୁଥିଲେ, ଦର୍ଶାଅ ଯେ ତ୍ରିଭୁଜଟି ସମଦ୍ବିବାହୁ ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ ∠A ର ସମଦ୍ୱିଖଣ୍ଡକ \(\overrightarrow{\mathrm{AD}}\), B͞C କୁ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରେ
ପ୍ରାମାଣ୍ୟ : AB = AC ଅର୍ଥାତ୍ A ABC ସମଦ୍ବିବାହୁ ।
ଅଙ୍କନ : \(\overrightarrow{\mathrm{AD}}\) ଉପରେ E ଏପରି ଏକ ବିନ୍ଦୁ ଯେପରିକି A – D – E ଏବଂ AD = DE | C͞E ଅଙ୍କନ କର ।
ପ୍ରମାଣ : Δ ABD ଓ Δ CDE ଦ୍ଵୟରେ AD = DE (ଅଙ୍କନ)
BD = DC (ଦତ୍ତ) ଏବଂ m∠ADB = m∠CDE (ପ୍ରତୀପ)
∴ Δ ABD = Δ CDE (କୋ-ବା-କୋ ସର୍ବସମତା)
⇒ AB = CE ଏବଂ m∠BAD = m∠CED … (i)
m∠BAD = m∠CAD (ଦତ୍ତ)
m∠CED = m∠CAD ⇒ AC = CE … (ii)
∴ (i) ଓ (ii) ରୁ AB = AC
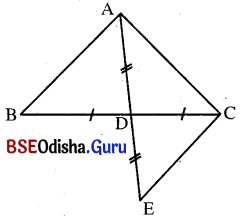(ପ୍ରମାଣିତ)
Question 22.
Δ ABC ଓ Δ DEF ରେ X ଓ Y ଯଥାକ୍ରମେ B͞C ଓ E͞F ର ମଧ୍ୟବିନ୍ଦୁ । AB = DF, BC = EF ଓ AX = DY ହେଲେ ପ୍ରମାଣ କର ଯେ, Δ ABC ≅ Δ DEF ।
ସମାଧାନ:
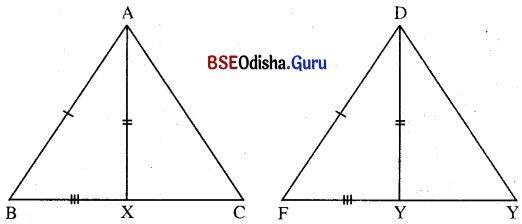
ଦତ୍ତ : X, B͞C ର ମଧ୍ୟବିନ୍ଦୁ ଏବଂ Y, B͞C ର ମଧ୍ୟବିନ୍ଦୁ, AX = DY, AB = DF ଏବଂ BC = EF ।
ପ୍ରାମାଣ୍ୟ : Δ ABC ≅ Δ DEF
ପ୍ରମାଣ : Δ ABX ଓ Δ DFY ମଧ୍ୟରେ, AB = DF, AX = DY ଏବଂ BX = FY
(∵ BC = FE ଏବଂ X ଓ Y ଯଥାକ୍ରମେ B͞C ଓ F͞E ର ମଧ୍ୟବିନ୍ଦୁ)
∴ Δ ABC ≅ Δ DEF (ବା-ବା-ବା ସର୍ବସମତା )
⇒ m∠ABX = m∠DFY ⇒ m∠ABC = m∠DFE
ଟର୍ଭମାନ Δ ABC ଓ Δ DFE ଦ୍ଵୟରେ, AB = DF, BC = FE ଏବଂ m∠ABC = m∠DFE
∴ Δ ABC = Δ DFE (ବା-କୋ-ବା ସ୍ଵୀକାର୍ଯ୍ୟ) (ପ୍ରମାଣିତ)
Question 23.
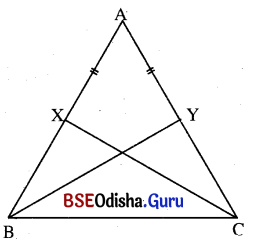
Δ ABC ରେ AB = AC । X ଓ Y ଯଥାକ୍ରମେ A͞B ଓ A͞C ଉପରିସ୍ଥ ଦୁଇଟି ବିନ୍ଦୁ ଯେପରିକି AX = AY ।
ପ୍ରମାଣ କର ଯେ, CX = BY ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ AB = AC । A͞B ଓ A͞C ଉପରିସ୍ଥ X ଓ Y ଏପରି ଏକ ବିନ୍ଦୁ ଯେପରିକି AX = AY ।
ପ୍ରାମାଣ୍ୟ : CX = BY
ପ୍ରମାଣ : Δ ABY ଏବଂ Δ ACX ଦ୍ଵୟରେ AB = AC (ଦତ୍ତ)
AY = AX (ଦତ୍ତ) , m∠BAY = m∠CAX (ସାଧାରଣ କୋଣ)
∴ Δ ABY ≅ Δ ACX (ବା-କୋ-ବା ସର୍ବସମତା)
⇒ BY = CX ⇒ CX = BY
(ପ୍ରମାଣିତ)
Question 24.
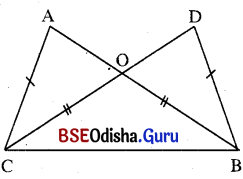
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ AB = CD ଓ AC = BD । ପ୍ରମାଣ କର ଯେ AO = DO ଓ BO = CO ।
ସମାଧାନ:
ଦତ୍ତ : ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ AB = CD, AC = BD ।
ପ୍ରାମାଣ୍ୟ : AO = DO ଏବଂ BO = CO ।
ପ୍ରମାଣ : Δ ACB ଏବଂ Δ DBC ଦ୍ୱୟରେ
AB = CD (ଦତ୍ତ), AC = BD (ଦତ୍ତ) ଏବଂ C͞B (ସାଧାରଣ ବାହୁ)
∴ Δ ACB ≅ Δ DBC (ବା-କୋ-ବା ସ୍ଵୀକାର୍ଯ୍ୟ)
⇒ m∠CAB = m∠CDB ଓ m∠ABC = m∠DCB
⇒ m∠OBC = m∠OCB ⇒ BO = CO
⇒ AB = CD (ଦତ୍ତ) ⇒ AO + BO = CO + DO ⇒ AO = DO (∵ BO = CO)
(ପ୍ରମାଣିତ)
Question 25.
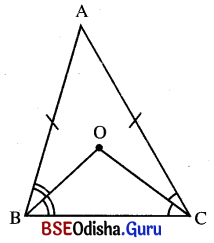
Δ ABC ରେ AB = AC । ∠ABC ଓ ∠ACB କୋଣର ସମଦ୍ବିଖଣ୍ଡକଦ୍ୱୟ ପରସ୍ପରକୁ ‘O’ ବିନ୍ଦୁରେ ଛେଦ କରୁଥିଲେ ଦର୍ଶାଅ ଯେ, Δ OBC ସମଦ୍ବିବାହୁ ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ AB = AC ।
∠ABC ଓ ∠ACB କୋଣର ସମଦ୍ବିଖଣ୍ଡକଦ୍ୱୟ ପରସ୍ପରକୁ ‘O’ ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
ପ୍ରାମାଣ୍ୟ : Δ OBC ସମଦ୍ବିବାହୁ । ଅର୍ଥାତ୍ OB = OC ।
ପ୍ରମାଣ : Δ ABC ରେ AB = AC
⇒ m∠ACB = m∠ABC (ସମାନ ବାହୁର ସମ୍ମୁଖୀନ କୋଣ ସମାନ)
⇒ \(\frac{1}{2}\)m∠ACB = \(\frac{1}{2}\)m∠ABC ⇒ m∠OCB = m∠OBC (ଦତ୍ତ)
⇒ OB = OC
ଅର୍ଥାତ୍ OBC ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।
(ପ୍ରମାଣିତ)
Question 26.
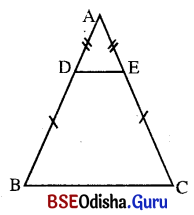
Δ ABC ରେ AB ଓ AC ଉପରେ ଯଥାକ୍ରମେ D ଓ E ଏପରି ଦୁଇଟି ବିନ୍ଦୁ ଯେପରିକି AD = AE ଏବଂ DB = EC । ଦର୍ଶାଅ ଯେ, DE || BC ।
ସମାଧାନ :
ଦତ୍ତ : Δ ABC ରେ AB ଓ AC ଉପରେ ଯଥାକ୍ରମେ D ଓ E ଦୁଇଟି ବିନ୍ଦୁ
ଯେପରିକି AD = AE ଓ DB = EC ।
ପ୍ରାମାଣ୍ୟ : DE || BC ।
ପ୍ରମାଣ : Δ ADE ରେ AD = AE (ଦତ୍ତ)
⇒ m∠ADE = m∠AED (ଭୁମି ସଂଲଗ୍ଶ କୋଣ)
AD + BD = AE + EC ⇒ AB = AC ⇒ m∠B = m∠C
Δ ADE ରେ m∠A + m∠ADE + m∠AED = 180°
m∠A + 2m∠ADE = 180° (∵ m∠ADE = m∠AED) … (i)
Δ ABC ରେ m∠A + m∠B + m∠C = 180°
m∠A + 2m∠B = 180° (m∠C = m∠B) … (ii)
(i) ଓ (ii) ରୁ m∠A + 2m∠ADE = m∠A + 2m∠B
2m∠ADE = 2m∠B ⇒ m∠ADE = m∠B
କିନ୍ତୁ ଏହି କୋଣଦ୍ଵୟ ଏକାନ୍ତର ଅଟନ୍ତି ।
∴ DB = EC ।
(ପ୍ରମାଣିତ)