Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 2 ତ୍ରିଭୁଜମାନଙ୍କ ସର୍ବସମତା Ex 2(b) Textbook Exercise Questions and Answers.
BSE Odisha Class 9 Maths Solutions Geometry Chapter 2 ତ୍ରିଭୁଜମାନଙ୍କ ସର୍ବସମତା Ex 2(b)
Question 1.
ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।
(a) Δ ABC ରେ m∠A = 40°, m∠B = 75° ହେଲେ, ତ୍ରିଭୁଜର ବୃହତ୍ତମ ଏବଂ କ୍ଷୁଦ୍ରତମ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ବାହୁମାନ ସ୍ଥିର କର ।
ସମାଧାନ:
m∠A = 40°, m∠B = 75°
⇒ Δ ABCର m∠C = (180 – 40 – 75)° = 65°
m∠B > m∠C > m∠A
⇒ AC > AB > BC
∴ ବୃହତ୍ତମ ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ବାହୁ AC ଓ କ୍ଷୁଦ୍ରତମ ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ବାହୁ BC ।
(b) Δ ABC ରେ m∠A = 110°, m∠B = 20° ହେଲେ, ତ୍ରିଭୁଜର କେଉଁ ବାହୁଟି କ୍ଷୁଦ୍ରତମ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ?
ସମାଧାନ:
Δ ABC ରେ m∠A = 110°, m∠B = 20° ∴ m∠C = (180 – 110 – 20)° = 50°
m∠A > m∠C > m∠B
⇒ BC > AB > AC
∴ AC କ୍ଷୁଦ୍ରତମ ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ବାହୁ ।
(c) Δ ABC ରେ m∠B = 90° ହେଲେ, ତ୍ରିଭୁଜର କେଉଁ ବାହୁଟି ବୃହତ୍ତମ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ?
ସମାଧାନ:
Δ ABC ରେ m∠B = 90° ।
⇒ m∠C < 90° ଓ m∠A < 90°
∴ ∠B ର ସମ୍ମୁଖୀନ ବାହୁ AC ବାହୁଟି ବୃହତ୍ତମ ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ।
(d) Δ ABC ରେ m∠A = m∠B + m∠C ହେଲେ, ତ୍ରିଭୁଜର ବୃହତ୍ତମ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ବାହୁ କେଉଁଟି ?
ସମାଧାନ:
Δ ABC ରେ m∠A = m∠B + m∠C
ଆମେ କଣ୍ଙ m∠A + m∠B + m∠C = 180°
⇒ m∠A = m∠B + m∠C = 90°
∴ ∠A ର ସମ୍ମୁଖୀନ ବାହୁ BC ର ବୃହତ୍ତମ ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ବାହୁ ।
(e) Δ ABC ରେ m∠A = 40°, m∠B = 50° । ବାହୁଗୁଡ଼ିକର ଦୈର୍ଘ୍ୟର ଉକ୍ରମରେ ସଜାଇ ଲେଖ ।
ସମାଧାନ:
Δ ABC ରେ m∠A = 40°, m∠B = 50° ⇒ m∠C = 180° – 40° – 50° = 90°
∴ m∠C > m∠B > m∠A
⇒ AB > AC > BC
![]()
Question 2.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(a) ତ୍ରିଭୁଜର ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି, ଏହାର ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟଠାରୁ ________ ।
ସମାଧାନ:
ବୃହତ୍ତର
(b) ତ୍ରିଭୁଜର ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟର ଅନ୍ତର, ଏହାର ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟଠାରୁ ________ ।
ସମାଧାନ:
କ୍ଷୁଦ୍ରତର
(c) ତ୍ରିଭୁଜର ଉଚ୍ଚତା ତ୍ରୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି, ଏହାର ପରିସୀମାଠାରୁ ________ ।
ସମାଧାନ:
କ୍ଷୁଦ୍ରତର
(d) ତ୍ରିଭୁଜର ପରିସୀମା, ଏହାର ମଧ୍ୟମାତ୍ରୟର ସମଷ୍ଟିଠାରୁ ________ ।
ସମାଧାନ:
ବୃହତ୍ତର
(e) ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁରୁ ଭୂମିପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ ଏହାର ଅନ୍ୟ ଦୁଇ ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟଠାରୁ ________ ।
ସମାଧାନ:
କ୍ଷୁଦ୍ରତର
Question 3.
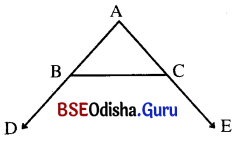
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ m∠CBD > m∠BCE ହେଲେ, ଦର୍ଶାଅ ଯେ AB > AC ।
ସମାଧାନ:
ଦତ୍ତ : ଚିତ୍ରରେ m∠CBD > m∠BCE
ପ୍ରାମାଣ୍ୟ : AB > AC
ପ୍ରମାଣ : m∠CBD > m∠BCE
⇒ m∠A + m∠ACB > m∠A + m∠ABC
(∵ ତ୍ରିଭୁଜର ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ଅନ୍ତଃସ୍ଥ ଦୂରବର୍ତ୍ତୀ କୋଣଦ୍ୱୟର ପରିମାଣର ସମଷ୍ଟି ସହ ସମାନ)
⇒ m∠ACB > m∠ABC ⇒ AB > AC
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 4.
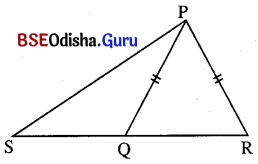
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ PQ = PR । ଦର୍ଶାଅ ଯେ PS > PQ ।
ସମାଧାନ:
ଦତ୍ତ : ଚିତ୍ରରେ PQ = PR
ପ୍ରାମାଣ୍ୟ : PS > PQ
ପ୍ରମାଣ : PQ = PR ⇒ m∠PRQ = m∠PQR … (i)
m∠PQR > m∠PSQ
(∵ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ଅନ୍ତଃସ୍ଥ ଦୂରବର୍ତ୍ତୀ କୋଣର ପରିମାଣଠାରୁ ବୃହତ୍ତର)
⇒ m∠PQR >m∠PSR ⇒ m∠PRQ > m∠PSR (∵ m∠PRQ = m∠PQR)
⇒ m∠PRS > m∠PSR ⇒ PS > PR
⇒ PS > PQ (∵ PQ = PR)
![]()
Question 5.
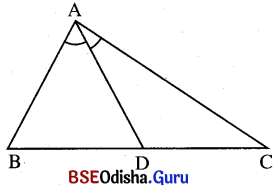
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ A͞D, ∠A ର ସମଦ୍ବିଖଣ୍ଡକ ହେଲେ, ଦର୍ଶାଅ ଯେ (i) AB > BD (ii) AC > CD ।
ସମାଧାନ:
ଦତ୍ତ : ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ A͞D, ∠A ର ସମଦ୍ବିଖଣ୍ଡକ ।
ପ୍ରାମାଣ୍ୟ : (i) AB > BD ଏବଂ (ii) AC > CD
ପ୍ରମାଣ : Δ ADC ରେ m∠ADB > m∠CAD
m∠ADB > m∠BAD (∵ m∠BAD = m∠CAD)
AB > BD … (i)
ପୁନଶ୍ଚ, Δ ABD ରେ m∠ADC > m∠BAD
m∠ADC > m∠CAD (∵ m∠CAD = m∠BAD)
AC > CD … (ii)
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 6.
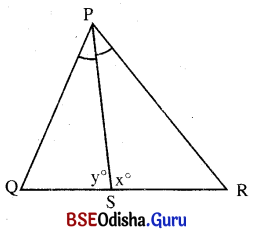
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ PR > PQ ଏବଂ P͞S, ∠P ର ସମଦ୍ବିଖଣ୍ଡକ । ଦର୍ଶାଅ ଯେ x > y ।
ସମାଧାନ:
ଦତ୍ତ : ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ PR > PQ । P͞S, ∠P ର ସମଦ୍ଵିଖଣ୍ଡକ ।
ପ୍ରାମାଣ୍ୟ : x > y
ପ୍ରମାଣ : PQR ରେ PR > PQ ⇒ m∠POS > m∠PRS … (i)
APQS ରେ ବହିଃସ୍ଥ m∠PSR = m∠PQS + m∠QPS
APSR ରେ ବହିଃସ୍ଥ m∠PSQ = m∠PRS + m∠RPS
କିନ୍ତୁ (i) ରୁ m∠PQS > m∠PRS
⇒ m∠PQS + m∠QPS > m∠PRS + m∠RPS (∵ m∠QPS = m∠RPS)
⇒ m∠PSR > m∠PSQ ⇒ x > y
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 7.
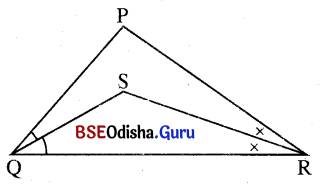
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ PQ > PR, \(\overrightarrow{\mathrm{QS}}\) ଏବଂ \(\overrightarrow{\mathrm{RS}}\) ଯଥାକ୍ରମେ ∠Q ଓ ∠R ର ସମଦ୍ବିଖଣ୍ଡକ । ଦର୍ଶାଅ ଯେ SQ > SR ।
ସମାଧାନ:
ଦତ୍ତ : ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ PQ > PR ।
\(\overrightarrow{\mathrm{QS}}\) ଏବଂ \(\overrightarrow{\mathrm{RS}}\) ଯଥାକ୍ରମେ ∠Q ଓ ∠R ର ସମଦ୍ବିଖଣ୍ଡକ ।
ପ୍ରାମାଣ୍ୟ : SQ > SR
ପ୍ରମାଣ : PQ > PR ⇒ m∠PRQ > m∠PQR
\(\frac{1}{2}\)m∠PRQ > \(\frac{1}{2}\)m∠PQR ⇒ m∠SRQ > m∠SQR
⇒ SQ > SR
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 8.
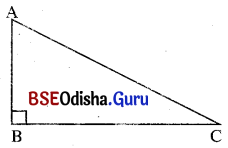
ଦର୍ଶାଅ ଯେ, ସମକୋଣୀ ତ୍ରିଭୁଜର କର୍ଣ୍ଣ ତ୍ରିଭୁଜର ବୃହତ୍ତମ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ବାହୁ ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ m∠B = 90° ।
ପ୍ରାମାଣ୍ୟ : A͞C, ତ୍ରିଭୁଜର ବୃହତ୍ତମ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ବାହୁ ।
ପ୍ରମାଣ : m∠ABC = 90°
⇒ m∠BAC +m∠ACB = 90°
∴ m∠ABC > m∠BAC ⇒ AC > BC … (i)
ପୁନଣ୍ଚ, m∠ABC > m∠ACB ⇒ AC > AB … (ii)
∴ (i) ଓ (ii) ରୁ A͞C ବୃହତ୍ତମ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ବାହୁ ।
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
![]()
Question 9.
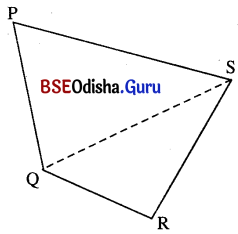
PQRS ଚତୁର୍ଭୁଜରେ P͞S ଓ Q͞R ଯଥାକ୍ରମେ ଚତୁର୍ଭୁଜର ବୃହତ୍ତମ ଏବଂ କ୍ଷୁଦ୍ରତମ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ବାହୁ । ପ୍ରମାଣ କର ଯେ,
(i) m∠PQR > m∠PSR
(ii) m∠QRS > m∠SPQ ଏବଂ
(iii) m∠P + m∠S < m∠Q + m∠R
ସମାଧାନ:
ଦତ୍ତ : PQRS ଚତୁର୍ଭୁଜରେ P͞S ଓ Q͞R ଯଥାକ୍ରମେ ଚତୁର୍ଭୁଜର ବୃହତ୍ତମ ଏବଂ କ୍ଷୁଦ୍ରତମ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ବାହୁ ।
ପ୍ରାମାଣ୍ୟ : (i) m∠PQR > m∠PSR
(ii) m∠QRS > m∠SPQ ଏବଂ
(iii) m∠P + m∠S < m∠Q + m∠R
ଅଙ୍କନ : S͞Q ଅଙ୍କନ କର ।
ପ୍ରମାଣ : Δ PSQ ରେ m∠PQS > m∠PSQ
(:: P͞S ବୃହତ୍ତମ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ବାହୁ)
Δ QSR ରେ m∠SQR > m∠QSR
(: Q͞R କ୍ଷୁଦ୍ରତମ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ବାହୁ)
⇒ m∠PQS + m∠SQR > m∠PSQ + m∠QSR
⇒ m∠PQR > m∠PSR … (i)
ସେହିପରି P͞R ଅଙ୍କନ କରି ପ୍ରମାଣ କରାଯାଇପାରେ ଯେ,
m∠QRS > m∠SPQ … (ii)
(i) ଓ (ii) ରୁ m∠PQR + m∠QRS > m∠PSR + m∠SPQ
⇒ m∠Q + m∠R > m∠S + m∠P
⇒ m∠S + m∠P < m∠Q + m∠R … (iii)
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 10.
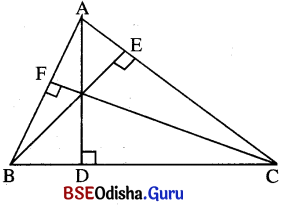
Δ ABC ର AD, BE ଓ CF ଉଚ୍ଚତାତ୍ରେୟ । ପ୍ରମାଣ କର ଯେ,
(i) AB + AC > 2AD
(ii) AB + BC + AC > AD + BE + CF
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ର A͞D ⊥ B͞C, BE ⊥ AC ଏବଂ CF ⊥ AB
ପ୍ରାମାଣ୍ୟ : (i) AB + AC > 2AD
(ii) AB + BC + AC > AD + BE + CF
ପ୍ରମାଣ : Δ ABD ରେ AB > AD ଏବଂ Δ ADC ରେ AC > AD
⇒ AB + AC > 2AD … (i)
ସେହିପରି ପ୍ରମାଣ କରାଯାଇ ପାରେ ଯେ, AC + BC > 2CF ଏବଂ AB + BC > 2BE
∴ AB + AC + AC + BC + AB + BC > 2AD + 2CF + 2BE
⇒ 2(AB + AC + BC) > 2(AD + BE + CF)
⇒ AB + AC + BC > AD + BE + CF … (ii)
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 11.
Δ ABC ର AD, BE ଏବଂ CF ମଧ୍ଯମାତ୍ରୟ । ପ୍ରମାଣ କର ଯେ,
(i) AB + AC > 2AD
ସମାଧାନ:
ଦତ୍ତ : (i) Δ ABC ରେ AD ମଧ୍ୟମା ।
ପ୍ରାମାଣ୍ୟ : AB + AC > 2AD
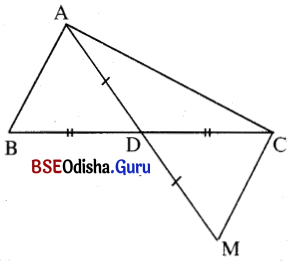
ଅଙ୍କନ : \(\overrightarrow{\mathrm{AD}}\) ଉପରେ M ଏପରି ଏକ ବିନ୍ଦୁ ଯେପରିକି AD = DM ହେବ । CM ଅଙ୍କନ କର ।
ପ୍ରମାଣ : Δ ABD ଓ Δ CDM ଦ୍ବୟରେ BD = CD (ଦତ୍ତ),
AD = DM (ଅଙ୍କନ) ଏବଂ m∠ADB = m∠CDM (ପ୍ରତୀପ)
Δ ABD ≅ Δ CDM => AB = CM … (i)
ବର୍ଭମାନ Δ ACM ରେ AC + CM > AM
AC + CM > 2AD => AC + AB > 2AD … (i) ରୁ
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
(ii) AB + AC + BC > AD + BE + CF
ସମାଧାନ:
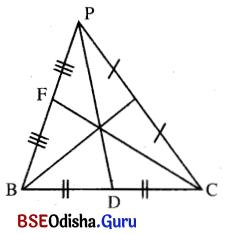
ଦତ୍ତ : Δ ABC ର AD, BE ଓ CF ମଧ୍ଯମାତ୍ରୟ ।
ପ୍ରାମାଣ୍ୟ : AB+ AC + BC > AD + BE + CF
ପ୍ରମାଣ : (i) ରେ ପ୍ରମାଣିତ ଯେ, AB + AC > 2AD
ସେହିପରି ପ୍ରମାଣ କରାଯାଇପାରେ,
AB + BC > 2BE ଏବଂ BC + AC > 2BF
∴ AB + AC + AB + BC + BC + AC > 2AD + 2BE + 2CF
⇒ 2(AB + AC + BC) > 2(AD + BE + CF)
⇒ AB + AC + BC > AD + BE + CF … (ii)
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
![]()
Question 12.
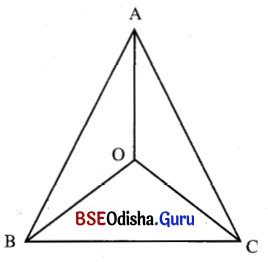
Δ ABC ର O ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ହେଲେ, ପ୍ରମାଣ କର ଯେ
(i) BO + CO < AB + AC
ସମାଧାନ:
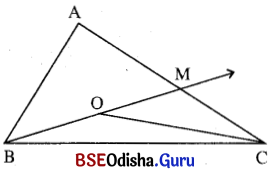
ଦତ୍ତ : Δ ABC ର O ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : BO + CO < AB + AC
ଅଙ୍କନ : \(\overrightarrow{\mathrm{BO}}\), A͞C କୁ M ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
ପ୍ରମାଣ : Δ MOC ରେ OM + MC > CO, Δ ABM ରେ AB + AM > BM
∴ AB + AM + MC + OM > CO + BM ⇒ AB + AC + OM > CO + BO + OM
⇒ AB + AC > CO + BO ⇒ BO + CO < AB + AC … (i)
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
(ii) AO + BO + CO < AB + AC + BC ଏବଂ
ସମାଧାନ:
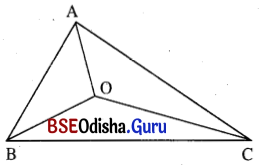
ଦତ୍ତ : Δ ABC ର O ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : AO + BO + CO < AB + AC + BC
ପ୍ରମାଣ : (i) ରେ ପ୍ରମାଣିତ BO + CO < AB + AC
ସେହିପରି ପ୍ରମାଣ କରାଯାଇପାରେ,
AO + CO < AB + BC ଏବଂ AO + BO < AC + BC
⇒ BO + CO + AO + CO + AO + BO < AB + AC + AB + BC + AC + BC
⇒ 2(AO + BO + CO) < 2(AB + AC + BC)
⇒ AO + BO + CO < AB + AC + BC … (ii)
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
(iii) AO + BO + CO > \(\frac{1}{2}\)(AB + AC + BC)
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ର O ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : AO + BO + CO > \(\frac{1}{2}\)(AB + AC + BC)
ପ୍ରମାଣ : Δ AOB ରେ AO + BO > AB, Δ BOC ରେ BO + CO > BC
Δ AOC ରେ AO + CO > AC
∴ AO + BO + BO + CO + AO + CO > AB + BC + AC
⇒ 2(AO + BO + CO) > AB + BC + AC
⇒ AO + BO + CO > \(\frac{1}{2}\)(AB + AC + BC) … (iii)
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 13.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ Δ ABC ରେ AB > AC ଏବଂ AD = AC । ପ୍ରମାଣ କର ଯେ,
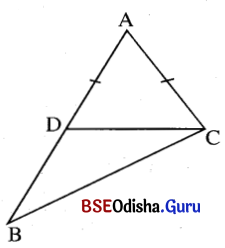
(i) m∠ACD = \(\frac{1}{2}\) (m∠B + m∠C)
(ii) m∠BCD = \(\frac{1}{2}\) (m∠C – m∠B)
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ AB > AC ଏବଂ AD = AC ।
ପ୍ରାମାଣ୍ୟ : (i) m∠ACD = \(\frac{1}{2}\) (m∠B + m∠C)
(ii) m∠BCD = \(\frac{1}{2}\) (m∠C – m∠B)
ପ୍ରମାଣ : (i) Δ ADC ରେ AD = AC
⇒ m∠ADC = m∠ACD ⇒ 2m∠ADC = 2m∠ACD
⇒ m∠ADC + m∠ADC = 2m∠ACD
⇒ m∠ADC + m∠DBC + m∠DCB = 2m∠ACD
⇒ (m∠ACD + m∠DCB) + m∠DBC = 2m∠ACD (∵ m∠ADC = m∠ACD)
⇒ m∠C + m∠B = 2m∠ACD
⇒ m∠ACD = \(\frac{1}{2}\) (m∠C + m∠B) … (i) (ପ୍ରମାଣିତ)
(ii) ପୁନଣ୍ଚ, m∠BCD = m∠ACB – m∠ACD
⇒ 2m∠BCD = 2m∠ACB – 2m∠ACD
⇒ 2m∠BCD = 2m∠ACB – m∠ACD – m∠ACD = 2m∠ACB – m∠ACD – m∠ADC
= 2m∠ACB – m∠ACD – (m∠DBC + m∠DCB)
= 2m∠ACB – m∠ACD – m∠DBC – m∠DCB
= 2m∠ACB – (m∠ACD + m∠DCB) – m∠DBC
= 2m∠ACB – m∠ACB – m∠DBC = m∠ACB – m∠DBC = m∠C – ∠B
m∠BCD = \(\frac{1}{2}\) (m∠C – m∠B) … (ii) (ପ୍ରମାଣିତ)
![]()
Question 14.
ABCD ଚତୁର୍ଭୁଜରେ ପ୍ରମାଣ କର ଯେ,
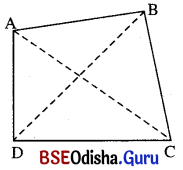
(i) AB + BC + CD > AD
ସମାଧାନ:
ଦତ୍ତ : ABCD ଚତୁର୍ଭୁଜ
ପ୍ରାମାଣ୍ୟ : AB + BC + CD > AD
ପ୍ରମାଣ : Δ ABC ରେ AB + BC > AC … (1)
Δ ADC ରେ AC + CD > AD … (2)
(1) ଓ (2) କୁ ଯୋଗକଲେ AB + BC + AC + CD > AC + AD
⇒ AB + BC + CD > AD (ଉଭୟ ପାର୍ଶ୍ଵରୁ AC ବାଦଦେଲେ) (ପ୍ରମାଣିତ)
(ii) AB + BC + CD + AD > AC + BD
ସମାଧାନ:
ଦତ୍ତ : ABCD ଏକ ଚତୁର୍ଭୁଜ
ପ୍ରାମାଣ୍ୟ : AB + BC + CD + AD > AC + BD
ପ୍ରମାଣ : Δ ABC ରେ AB + BC > AC … (1)
Δ BDC ରେ BC + CD > BD … (2)
Δ ADC ରେ AD + CD > AC … (3)
Δ ADB ରେ AD + AB > BD … (4)
( 1), (2), (3) ଓ (4) କୁ ଯୋଗକଲେ
AB + BC + BC + CD + AD + CD + AD + AB > AC + AC + BD + BD
⇒ 2(AB + BC + CD + AD) > 2(AC + BD)
⇒ AB + BC + CD + AD > AC + BD (ପ୍ରମାଣିତ)
(ii) AB + BC + CD + AD > AC + BD
ସମାଧାନ:
ଦତ୍ତ : ABCD ଏକ ଚତୁର୍ଭୁଜ
ପ୍ରାମାଣ୍ୟ : AB + BC + CD + AD > 2AC
ପ୍ରମାଣ : ABC Δରେ AB + BC > AC … (1)
ସେହିପରି ADC Δରେ AD + CD > AC … (2)
(1) ଓ (2) କୁ ଯୋଗକଲେ AB + BC + CD + AD > AC + AC
⇒ AB + BC + CD + AD > 2AC (ପ୍ରମାଣିତ)
Question 15.
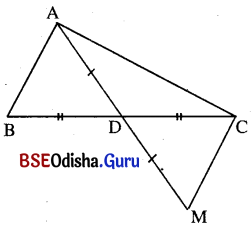
Δ ABC ରେ AC > AB ଏବଂ A͞D ତ୍ରିଭୁଜର ମଧ୍ୟମା ହେଲେ ପ୍ରମାଣ କର ଯେ m∠BAD > m∠CAD ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ AC > AB । A͞D, Δ ABC ର ଏକ ମଧ୍ୟମା ।
ପ୍ରାମାଣ୍ୟ : m∠BAD > m∠CAD
ଅଙ୍କନ : \(\overrightarrow{\mathrm{AD}}\) ଉପରେ M ଏପରି ଏକ ବିନ୍ଦୁ ଯେପରିକି AD = DM ।
CM ଅଙ୍କନ କର ।
ପ୍ରମାଣ : Δ ABD ଓ Δ CMD ଦ୍ବୟରେ BD = CD,
AD = DM ଏବଂ m∠ADB = m∠CDM (ପ୍ରତୀପ)
∴ Δ ABD ≅ ACMD ⇒ AB = CM ଏବଂ m∠CMD = m∠BAD
∴ Δ ACM ରେ AC > CM (∵ AC > AB ଦତ୍ତ)
⇒ m∠CMD > m∠CAD
⇒ m∠BAD > m∠CAD (∵ m∠CMD = m∠BAD) (ପ୍ରମାଣିତ)
Question 16.
ABCD ଚତୁର୍ଭୁଜର ‘O’ ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ (କର୍ଣ୍ଣଦ୍ୱୟର ଛେଦବିନ୍ଦୁ ଭିନ୍ନ) ହେଲେ ପ୍ରମାଣ କର ଯେ,
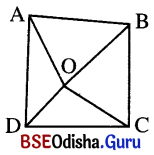
(i) 2(OA + OB + OC + OD) > AB + BC + CD + AD ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଏକ ଚତୁର୍ଭୁଜର ଅନ୍ତର୍ଦେଶରେ ‘O’ ଏକ ବିନ୍ଦୁ । ଯାହା କର୍ଣ୍ଣଦ୍ଵୟର ଛେଦବିନ୍ଦୁ ନୁହେଁ ।
ପ୍ରାମାଣ୍ୟ : 2(OA + OB + OC + OD) > AB + BC + CD + AD
ପ୍ରମାଣ : Δ AOB ରେ OA + OB > AB … (i)
Δ AAD ରେ OA + OD > AD … (ii)
Δ ADC ରେ OD + OC > CD … (iii)
Δ ABC ରେ OB + OC > BC … (iv)
(i), (ii), (iii) ଓ (iv) କୁ ଯୋଗକଲେ
OA + OB + OA + OD + OD + OC + OB + OC > AB + AD + CD + BC
⇒ 2(OA + OB + OC + OD) > AB + BC + CD + AD (ପ୍ରମାଣିତ)
(ii) OA + OB + OC + OD > AC + BD
ସମାଧାନ:
ଦତ୍ତ : ABCD ଚତୁର୍ଭୁଜରେ ‘O’ ଏକ ଅନ୍ତସ୍ଥ ବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : OA + OB + OC + OD > AC + BD
ପ୍ରମାଣ : Δ AOC ରେ OA + OC > AC … (1)
Δ BOD ରେ OB + OD > BD … (2)
(1) ଓ (2) କୁ ଯୋଗକଲେ
OA + OC + OB + OD > AC + BD
OA + OB + OC + OD > AC + BD (ପ୍ରମାଣିତ)
![]()
Question 17.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ m∠PAX = m∠QAY ହେଲେ ଦର୍ଶାଅ ଯେ, PA +AQ < PB + BQ ।
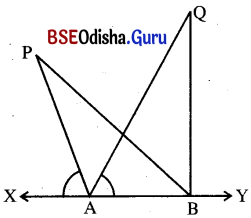
ସମାଧାନ:
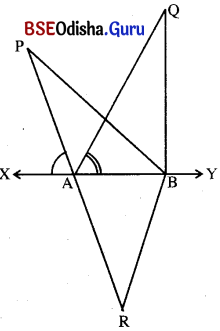
ଦତ୍ତ : ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ m∠PAX = m∠QAY ।
ପ୍ରାମାଣ୍ୟ : PA + AQ < PB + BQ
ଅଙ୍କନ : \(\overrightarrow{\mathrm{PA}}\) ଉପରେ R ଏକ ବିନ୍ଦୁ ନିଅ ଯେପରିକି P – A – R ଓ AQ = AR ହେବ ।
ପ୍ରମାଣ : m∠PAX = m∠BAR (ପ୍ରତୀପ କୋଣ)
m∠PAX = m∠QAY (ଦତ୍ତ)
⇒ m∠QAY = m∠BAR
∴ Δ ABQ ଓ Δ ABR ମଧ୍ୟରେ
AQ = AR (ଅଙ୍କନ)
m∠QAY = m∠BAR (ପ୍ରମାଣିତ)
A͞B ସଧାରଣ ବିନ୍ଦୁ
Δ ABQ ≅ Δ ABR (ବା-କୋ-ବା ସର୍ବସମତା)
⇒ BQ = BR
Δ PBR ରେ PR < PB + BR
⇒ PA + AR < PB + BR
⇒ PA + AQ < PB + BQ (∵ AR = AQ ଓ BR = BQ) (ପ୍ରମାଣିତ)
Question 17.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ AB = AC ହେଲେ ଦର୍ଶାଅ ଯେ, AF > AE ।
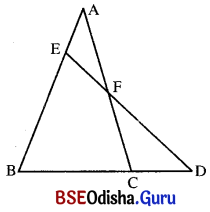
ସମାଧାନ:
ଦତ୍ତ : ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ AB = AC
ପ୍ରାମାଣ୍ୟ : AF > AE
ପ୍ରମାଣ : Δ ABC ରେ AB = AC (ଦତ୍ତ)
m∠ABC = m∠ACB
Δ DFC ରେ ବତ୍ହିଃସ୍ଥ m∠FCB > m∠CFD
⇒ m∠ACB > m∠CFD ⇒ m∠ACB > m∠AFE … (i)
[7 m∠AFE = m∠CFD (ପ୍ରତୀପ)]
⇒ m∠ABC > m∠AFE (∵ m∠ABC = m∠ACB)
ପୁନଶ୍ଚ ବତ୍ହିଃସ୍ଥ m∠AEF > m∠ABC
m∠AEF > m∠ACB (∵ m∠ABC = m∠ACB)
m∠AEF > m∠AFE [∵ (i) ରୁ]
⇒ AF > AE (ପ୍ରମାଣିତ)
