BSE Odisha 9th Class Maths Solutions Geometry Chapter 3 ଚତୁର୍ଭୁଜ Ex 3(a)

Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 3 ଚତୁର୍ଭୁଜ Ex 3(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Geometry Chapter 3 ଚତୁର୍ଭୁଜ Ex 3(a)

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଗୋଟିଏ ଉତ୍ତଳ ଚତୁର୍ଭୁଜର କୋଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି ________ ।
ସମାଧାନ:
360°

(ii) ଗୋଟିଏ ପଞ୍ଚଭୁଜର ଅନ୍ତଃସ୍ଥ କୌଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି ________ ।
ସମାଧାନ:
540°

(iii) ଗୋଟିଏ ଅଷ୍ଟଭୁଜର ବହିଃସ୍ଥ କୌଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି ________ ।
ସମାଧାନ:
360°

(iv) ଗୋଟିଏ ସୁଷମ ଷଡ଼ଭୁଜର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ ________ ।
ସମାଧାନ:
120°

(v) ଗୋଟିଏ ସୁଷମ ବହୁଭୁଜର ପ୍ରତ୍ୟେକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ 45° ହେଲେ ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା ________ ।
ସମାଧାନ:
8

(vi) ଗୋଟିଏ ସୁଷମ ବହୁଭୁଜର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ 150° ହେଲେ, ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା ________ ।
ସମାଧାନ:
12

(vii) ଗୋଟିଏ ସୁଷମ ବହୁଭୁଜର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି 1440° ହେଲେ, ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା ________ ।
ସମାଧାନ:
10

(viii) ଗୋଟିଏ ସୁଷମ ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା ୨ ହେଲେ, ଏହାର ପ୍ରତ୍ୟେକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ________ ।
ସମାଧାନ:
40°

(ix) n ସଂଖ୍ୟକ ବାହୁ ବିଶିଷ୍ଟ ଗୋଟିଏ ସୁଷମ ବହୁଭୁଜର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ ________ ।
ସମାଧାନ:
\(\frac{2 n-4}{n}\) × 90°

(x) n ସଂଖ୍ୟକ ବାହୁ ବିଶିଷ୍ଟ ଗୋଟିଏ ସୁଷମ ବହୁଭୁଜର ପ୍ରତ୍ୟେକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ________ ।
ସମାଧାନ:
\(\frac{360^{\circ}}{n}\)

Question 2.
(i) ଗୋଟିଏ ଚତୁର୍ଭୁଜର କୋଣମାନଙ୍କର ଅନୁପାତ 2 : 3 : 4 : 6 ହେଲେ, ସେମାନଙ୍କର ପରିମାଣ ସ୍ଥିର କର ।
ସମାଧାନ:
ମନେକର ଚତୁର୍ଭୁଜର କୋଣମାନଙ୍କର ପରିମାଣ 2x°, 3x°, 4x° ଏବଂ 6x° ।
∴ 2x° + 3x° + 4x° + 6x° = 360° ⇒ 15x  = 360° ⇒ x = 24
∴ 2x° = 2 × 24 = 48°, 3x° = 3 × 24 = 72°,
4x° = 4 × 24 = 96° ଏବଂ 6x° = 6 × 24 = 144°
∴ ଚତୁର୍ଭୁଜର କୋଣମାନଙ୍କର ପରିମାଣ 48°, 72°, 96° ଓ 144° ।

(ii) ଏକ ସାମାନ୍ତରିକ ଚିତ୍ରର ଦୁଇ କ୍ରମିକ କୋଣ ମଧ୍ୟରୁ ଗୋଟିକର ପରିମାଣ ଅନ୍ୟର ପରିମାଣର \(\frac{3}{2}\) ଗୁଣ ହେଲେ କୋଣଗୁଡ଼ିକର ପରିମାଣ ସ୍ଥିର କର ।
ସମାଧାନ:
ସାମାନ୍ତରିକ ଚିତ୍ରର ଦୁଇ ସନ୍ନିହିତ କୋଣଦ୍ଵୟର ପରିମାଣର ସମଷ୍ଟି 180° ।
ମନେକର ସାମାନ୍ତରିକ ଚିତ୍ରର ଗୋଟିଏ କୋଣର ପରିମାଣ x ଏବଂ ପ୍ରଶ୍ନନୁସାରେ ଅନ୍ୟଟିର ପରିମାଣ \(\frac{3 x^{\circ}}{2}\) ।
∴ x° + \(\frac{3 x^{\circ}}{2}\) = 180°
⇒ \(\frac{5 x^{\circ}}{2}\) = 180° ⇒ x = 72°
ଗୋଟିଏ କୋଣର ପରିମାଣ 72° ଏବଂ ଅନ୍ୟ କୋଣର ପରିମାଣ = \(\frac{3 x^{\circ}}{2}\) × 72 = 108°
∴ ସାମାନ୍ତରିକ ଚିତ୍ରର କୋଣଗୁଡ଼ିକର ପରିମାଣ 72°, 108°, 72° ଓ 108° ।

(iii) ଗୋଟିଏ ପଞ୍ଚଭୁଜର କୋଣମାନଙ୍କର ପରିମାଣର ଅନୁପାତ 2 : 3 : 4: 5 : 6 ହେଲେ ବୃହତ୍ତମ କୋଣର ପରିମାଣ ସ୍ଥିର କର ।
ସମାଧାନ:
n ବାହୁ ବିଶିଷ୍ଟ ଏକ ବହୁଭୂଜର ଅନ୍ତଃସ୍ଥ କୌଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି (2n – 4) ସମକୋଣ ।
ଗୋଟିଏ ପଞ୍ଚଭୁଜର ଅନ୍ତଃସ୍ଥ କୌଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି = (2 × 5 – 4) × 90° = 540°
ମନେକର ପଞ୍ଚଭୁଜର କୋଣମାନଙ୍କର ପରିମାଣ 2x°, 3x°, 4x°, 5x° ଏବଂ 6x° ।
∴ 2x° + 3x° + 4x° + 5x° + 6x° = 540° → 20x = 540 = x = 27
∴ ବୃହତ୍ତମ କୋଣର ପରିମାଣ = 6x = 6 × 27 = 162°

(iv) ଗୋଟିଏ ଉତ୍ତଳ ଚତୁର୍ଭୁଜର ଦୁଇଟି କୋଣ ସମକୋଣ ଏବଂ ଅନ୍ୟ କୋଣମାନଙ୍କର ପରିମାଣ ପ୍ରତ୍ୟେକ 120° ହେଲେ, ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା ସ୍ଥିର କର ।
ସମାଧାନ:
ମନେକର ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା n । 
∴ ଏହାର ଅନ୍ତଃସ୍ଥ କୌଣମାନଙ୍କ ସଂଖ୍ୟା n ।
ପ୍ରଶାନୁସାରେ, 90° + 90° + (n – 2) 120° = (2n – 4) × 90°
n ସଂଖ୍ୟକ ବାହୁବିଶିଷ୍ଟ ବହୁଭୁଜର ଅନ୍ତଃସ୍ଥ କୌଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି (2n – 4) ସମକୋଣ
ଏଠାରେ ଲକ୍ଷ୍ୟକର, ବହୁଭୁଜର n ସଂଖ୍ୟକ କୋଣ ମଧ୍ୟରୁ ଦୁଇଟି କୋଣ ସମକୋଣ ଏବଂ ଅନ୍ୟ ସମସ୍ତ କୋଣମାନ (n – 2 ସଂଖ୍ୟକ) ପ୍ରତ୍ୟେକେ 120° ।
⇒ 180 + (n – 2) 120 = (2n – 4) x 90
⇒ 18 + (n – 2) 12 = (2n – 4) 9
⇒ 18 + 12n – 24 = 18n – 36
⇒ 12n – 6 = 18n – 36
⇒  6n = 30 ⇒ n = 5
∴ ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା 5 ।

(v) ଗୋଟିଏ ପଞ୍ଚଭୁଜର କୋଣମାନଙ୍କର ପରିମାଣର x°, (x − 10°), (x − 20°), (2x – 40°), (2x – 90°) ହେଲେ ‘x’ ର ମାନ ସ୍ଥିର କର ।
ସମାଧାନ:
n ଭୁଜ ବିଶିଷ୍ଟ ବହୁଭୁଜର ଅନ୍ତଃସ୍ଥ କୌଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି (2n – 4) ସମକୋଣ । 
∴ ଗୋଟିଏ ପଞ୍ଚଭୁଜର ଅନ୍ତଃସ୍ଥ କୋଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି = (2 × 5 – 4) × 90° = 540°
⇒ 7x – 160 = 540 ⇒ 7x = 700 ⇒ x = 100

(vi) ଗୋଟିଏ ଅଷ୍ଟଭୁଜର ଅନ୍ତଃସ୍ଥ କୌଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି ଏବଂ ବହିଃସ୍ଥ କୌଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି ସ୍ଥିର କର ।
ସମାଧାନ:
ଗୋଟିଏ ଅଷ୍ଟଭୁଜର ଅନ୍ତଃ ସ୍ଥ କୋଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି = (2 × 8 – 4) × 90° = 1080°
ଏବଂ ବହିଃସ୍ଥ କୋଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି = 360°

(vii) ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ରର ଦୁଇ କ୍ରମିକ କୋଣଦ୍ୱୟର ପରିମାଣର ଅନୁପାତ 2 : 3 ହେଲେ ସାମାନ୍ତରିକ ଚିତ୍ରର ଅନ୍ୟ କୋଣମାନଙ୍କର ପରିମାଣ ସ୍ଥିର କର ।
ସମାଧାନ:
ସାମାନ୍ତରିକ ଚିତ୍ରର ଦୁଇ ସନ୍ନିହିତ କୋଣଦ୍ଵୟର ପରିମାଣର ସମଷ୍ଟି 180° ।
ମନେକର ଦୁଇ ସନ୍ନିହିତ କୋଣଦ୍ୱୟର ପରିମାଣ ଯଥାକ୍ରମେ 2x° ଏବଂ 3x° ।
∴ 2x + 3x = 180°
⇒ 5x = 180° ⇒ x = 36
∴ କୋଣମାନଙ୍କର ପରିମାଣ 2x° = 2 × 36 = 72° ଓ 3x° = 3 × 36 = 108°
∴ ସାମାନ୍ତରିକ ଚିତ୍ରର କୋଣମାନଙ୍କର ପରିମାଣ 72°, 108°, 72° ଏବଂ 108° ।

Question 3.
ଦର୍ଶାଅ ଯେ, ଗୋଟିଏ ସୁଷମ ଅଷ୍ଟଭୁଜର ଗୋଟିଏ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ ଏହାର ପ୍ରତ୍ୟେକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣର ତିନିଗୁଣ ।
ସମାଧାନ:
ସୁଷମ ବହୁଭୁଜ (n ବାହୁ ବିଶିଷ୍ଟ) ର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ =  \(\frac{2 n-4}{n}\) ସମକୋଣ ।
ଗୋଟିଏ ସୁଷମ ଅଷ୍ଟଭୁଜର ଗୋଟିଏ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ = \(\frac{2×8-4}{8}\) × 90° = \(\frac{12}{8}\) × 90 = 135°
ସୁଷମ ଅଷ୍ଟଭୁଜର ଗୋଟିଏ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ = \(=\frac{360^{\circ}}{n}\)
ସୁଷମ ଅଷ୍ଟଭୁଜର ଗୋଟିଏ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ = \(=\frac{360^{\circ}}{8}\) = 45°
ଏଠାରେ ଲକ୍ଷ୍ୟକର, 45° x 3 = 135° ହେତୁ ଅଷ୍ଟଭୁଜର ପ୍ରତ୍ୟେକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣର ତିନିଗୁଣ, ଏହାର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ ସହ ସମାନ ।

Question 4.
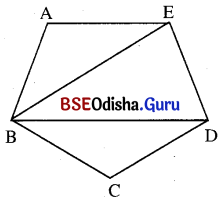
ABCDE ଗୋଟିଏ ସୁଷମ ପଞ୍ଚଭୁଜ ହେଲେ, Δ BED ର ପ୍ରତ୍ୟେକ କୋଣର ପରିମାଣ ସ୍ଥିର କର ।
ସମାଧାନ:
ABCDE ଗୋଟିଏ ସୁଷମ ପଞ୍ଚଭୁଜ ।
ସୁଷମ ବହୁଭୂଜ (n ବାହୁ ବିଶିଷ୍ଟ)ର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ = \(\frac{2 n-4}{n}\) ସମକୋଣ ।
ଏହାର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ = \(\frac{2×5-4}{5}\) × 90° = 108°
Δ ABE ରେ m∠A = 108°, m∠ABE = m∠AEB = \(\frac{72}{2}\) = 36°
∴ Δ BED ରେ m∠BED = m∠AED – m∠AEB
= 108° – 36° = 72°
ସେହିପରି m∠BDE = 72°
∴ Δ BDE ରେ m∠EBD = 180° – (72° + 72°) = 36°
∴ Δ BDE ର କୋଣଦ୍ୱୟର ପରିମାଣ 36°, 72°, 72°।

Question 5.
ଗୋଟିଏ ସୁଷମ ବହୁଭୁଜର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ ଏବଂ ବହିଃସ୍ଥ କୋଣର ପରିମାଣର ଅନୁପାତ 5 : 1 ହେଲେ, ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା ସ୍ଥିର କର ।
ସମାଧାନ:
ମନେକର ସୁଷମ ବହୁଭୁଜର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ = 5x°
ଓ ପ୍ରତ୍ୟେକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ = x°

⇒ n= 10 + 2
⇒ n= 12
∴ ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା 12 ।

Question 6.
n ସଂଖ୍ୟକ ବାହୁ ବିଶିଷ୍ଟ ଏକ ବହୁଭୁଜର ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ଓ (n + 2) ସଂଖ୍ୟକ ବାହୁ ବିଶିଷ୍ଟ ଏକ ବହୁଭୁଜର ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ମଧ୍ଯରେ ଅନ୍ତର 9° ହେଲେ, ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା ସ୍ଥିର କର ।
ସମାଧାନ:
n-ବାହୁ ବିଶିଷ୍ଟ ବହୁଭୁଜର ଏକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ = \(\frac{360^{\circ}}{n}\)

⇒ n² + 2n – 80 = 0
⇒ n² + 10n – 8n – 80 = 0
⇒ n(n + 10) – 8(n + 10) = 0
⇒ (n + 10)(n – 8) = 0
⇒ n = -10 କିମ୍ଚ‍।
ଏଠାରେ n = 8 ଗ୍ରହଣୀୟ କିନ୍ତୁ n = -10 ଗ୍ରହଣୀୟ ନୁହେଁ । 
∴ ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା 8 ।

Question 7.
ଗୋଟିଏ ସୁଷମ ବହୁଭୁଜର ଏକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ 120° ହେଲେ, ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା ସ୍ଥିର କର ।
ସମାଧାନ:
ମନେକର ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା n ।
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{2 n-4}{n}\) × 90° = 120°
ସୁଷମ ବହୁଭୁଜର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ = \(\frac{2 n-4}{n}\) ସମକୋଣ ।
⇒ (2n – 4) 9 = 12n
⇒ 18n – 36 = 12n
⇒ 6n = 36
⇒ n = 6
∴ ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା 6 ।

ବିକଳ୍ପ ସମାଧାନ :
ସୁଷମ ବହୁଭୁଜର ଏକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ 120° ।
ସୁଷମ ବହୁଭୁଜର ବହିଃସ୍ଥ କୋଣର ପରିମାଣ = 180° – 120° = 60° ।
n-ବାହୁ ବିଶିଷ୍ଟ ବହୁଭୁଜର ଏକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ = \(\frac{360^{\circ}}{n}\)
⇒ \(\frac{360^{\circ}}{n}\) = 60° 
⇒ 60° n = 360° 
⇒ n =\(\frac{360^{\circ}}{60}\) = 6
∴ ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା 6 ।

Question 8.
(n – 1) ସଂଖ୍ୟକ ଏବଂ (n + 2) ସଂଖ୍ୟକ ସୁଷମ ଚତୁର୍ଭୁଜର ବହିଃସ୍ଥ ବହୁଭୁଜର ବହିଃସ୍ଥ କୌଣଦ୍ୱୟର ଅନ୍ତର 6° ହେଲେ, ଦର୍ଶାଅ ଯେ, ‘n’ ର ମାନ 13 ହେବ ।
ସମାଧାନ:
n ସଂଖ୍ୟକ ବାହୁ ବିଶିଷ୍ଟ ଏକ ସୁଷମ ବହୁଭୁଜର ବହିଃସ୍ଥ କୋଣର ପରିମାଣ = \(\frac{360^{\circ}}{n}\)

⇒ n² + n – 2 = 180
⇒ n² + n – 182 = 0
⇒ n² + 14n – 13n – 182 = 0
⇒ n (n + 14) – 13(n + 14) = 0
⇒ (n + 14) (n- 13) = 0
⇒ n + 14 = 0 ବା n – 13 = 0
⇒ n = -14   ଅସମ୍ଭବ ∴ n = 13

Question 9.
ଗୋଟିଏ ପଞ୍ଚଭୁଜର ଗୋଟିଏ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ 140 । ଅନ୍ୟ କୋଣଗୁଡ଼ିକର ପରମାଣର ଅନୁପାତ 1 : 2 : 3 : 4 ହେଲେ ଦର୍ଶାଅ ଯେ, ବୃହତ୍ତମ କୋଣର ପରିମାଣ 160° ।
ସମାଧାନ:
n ବାହୁ ବିଶିଷ୍ଟ ଏକ ବହୁଭୁଜର ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣର ସମଷ୍ଟି (2n – 4) ସମକୋଣ ।
ଗୋଟିଏ ପଞ୍ଚଭୁଜର ଅନ୍ତଃସ୍ଥ କୌଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି = (2 × 5 – 4) × 90 = 540° 
ପଞ୍ଚଭୁଜର ଗୋଟିଏ କୋଣର ପରିମାଣ = 140°
ମନେକର ଅନ୍ୟ 4ଟି କୋଣର ପରିମାଣ x°, 2x°, 3x° ଓ 4x° ।
ପ୍ରଶ୍ନନୁସାରେ, x + 2x° + 3x° + 4x° + 140° = 540°
⇒ 10x = 400 ⇒ x = 40°
∴ ବୃହତ୍ତମ କୋଣର ପରିମାଣ = 4x° = 4 × 40° = 160°

Question 10.
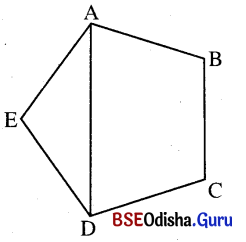
ABCDE ଗୋଟିଏ ସୁଷମ ପଞ୍ଚଭୁଜର AD, ∠CDE କୁ ଦୁଇଭାଗ କରୁଥିଲେ, ଦର୍ଶାଅ ଯେ m∠ADE : m∠ADC = 1 : 2 ।
ସମାଧାନ:
ଦତ୍ତ : ABCDE ଗୋଟିଏ ସୁଷମ ପଞ୍ଚଭୁଜର A͞D, ∠CDE କୁ ଦୁଇଭାଗ କରେ ।
ପ୍ରାମାଣ୍ୟ : m∠ADE : m∠ADC = 1 : 2 ।
ପ୍ରମାଣ : ସୁଷମ ପଞ୍ଚଭୁଜର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ = \(\frac{2 \times 5-4}{5}\) × 90 = \(\frac{6}{5}\) × 90° = 108°
AE = ED
⇒ m∠EAD = m∠EDA
m∠AED = 108° = m∠EDC
AAED ରେ m∠EAD = m∠ADE = \(\frac{180^{\circ}-108^{\circ}}{2}\) = \(\frac{72^{\circ}}{2}\) = 36°
m∠ADC = m∠EDC – m∠ADE = 108° – 36° = 72°
∴ m∠ADE : m∠ADC = 36° : 12°
⇒ m∠ADE : m∠ADC = 1 : 2
(ପ୍ରମାଣିତ)