Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 3 ଚତୁର୍ଭୁଜ Ex 3(b) Textbook Exercise Questions and Answers.
BSE Odisha Class 9 Maths Solutions Geometry Chapter 3 ଚତୁର୍ଭୁଜ Ex 3(b)
Question 1.
ନିମ୍ନଲିଖ ଉକ୍ତିଗୁଡ଼ିକ ଭୁଲ୍ କି ଠିକ୍ ଲେଖ ।
(a) ଚତୁର୍ଭୁଜର ଚାରୋଟି ବାହୁ ସର୍ବସମ ହେଲେ, ତାହା ଏକ ବର୍ଗଚିତ୍ର ।
ସମାଧାନ:
ଭୁଲ
(b) ପ୍ରତ୍ୟେକ ରମ୍ବସ୍ ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ସମାଧାନ:
ଠିକ୍
(c) ପ୍ରତ୍ୟେକ ସାମାନ୍ତରିକ ଚିତ୍ର ଏକ ରମ୍ବସ୍ ।
ସମାଧାନ:
ଭୁଲ
(d) ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ରର ଦୁଇ ସନ୍ନିହିତ ବାହୁର ଦୈର୍ଘ୍ୟ ସମାନ ହେଲେ, ତାହା ଏକ ରମ୍ବସ୍ ।
ସମାଧାନ:
ଠିକ୍
(e) ରମ୍ବସ୍ର କର୍ଣ୍ଣଦ୍ଵୟ ସର୍ବସମ ।
ସମାଧାନ:
ଭୁଲ
(f) ଗୋଟିଏ ଆୟତଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି ।
ସମାଧାନ:
ଠିକ୍
(g) ଗୋଟିଏ ରମ୍ବସ୍ର ଗୋଟିଏ କୋଣର ପରିମାଣ 90° ହେଲେ, ତାହା ଏକ ବର୍ଗଚିତ୍ର ।
ସମାଧାନ:
ଠିକ୍
(h) ଗୋଟିଏ ବର୍ଗଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରନ୍ତି ।
ସମାଧାନ:
ଠିକ୍
(i) ଯଦି ଏକ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ହୁଅନ୍ତି, ତେବେ ଚତୁର୍ଭୁଜଟି ଏକ ବର୍ଗଚିତ୍ର ।
ସମାଧାନ:
ଭୁଲ
(j) ପ୍ରତ୍ୟେକ ସାମାନ୍ତରିକ ଚିତ୍ର ଏକ ଟ୍ରାପିଜିୟମ୍ ।
ସମାଧାନ:
ଠିକ୍
(k) ପ୍ରତ୍ୟେକ ବର୍ଗଚିତ୍ର ଏକ ଆୟତଚିତ୍ର ।
ସମାଧାନ:
ଠିକ୍
(l) ରମ୍ବସ୍ ଏକ ବର୍ଗଚିତ୍ର ।
ସମାଧାନ:
ଭୁଲ
![]()
Question 2.
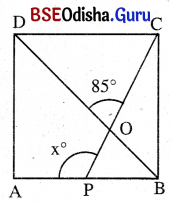
ନିମ୍ନ ଚିତ୍ରଗୁଡ଼ିକୁ ଦେଖ୍ ‘x’ ର ମୂଲ୍ୟ ସ୍ଥିର କର ।
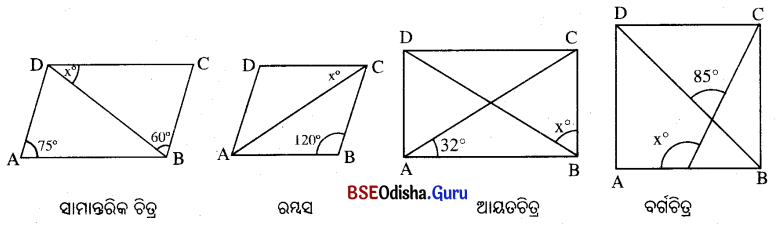
ସମାଧାନ:
ସାମାନ୍ତରିକ ଚିତ୍ର:
m∠DAB + m∠ABC = 180°
⇒ 75° + m∠ABD + m∠DBC = 180°
⇒ 75° + m∠ABD + 60° = 180°
⇒ m∠ABD = 180° – 135° = 45°
ବର୍ତ୍ତମାନ x = 45° (∵ m∠ABD = m∠CDB)
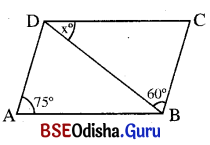
ରମ୍ବସ୍:
m∠ABC + m∠BCD = 180°
⇒ m∠BCD = 180° – m∠ABC = 180° – 120° = 60°
କିନ୍ତୁ Δ ABC ରେ m∠BAC + m∠BCA
= 180° – 120° = 60°
⇒ m∠BCA = \(\frac{60^{\circ}}{2}\) = 30° (∵ m∠BAC = m∠BCA)
m∠BCD = 60°
⇒ m∠BCA + m∠ACD = 60°
⇒ 30° + x = 60°
⇒ x = 30°
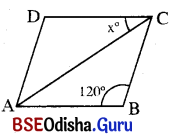
ଅ।ୟତଚିତ୍ର:
m∠BAC + m∠ACB = 90°
⇒ m∠ACB = 90° – m∠BAC = 90° – 32° = 58°
କିନ୍ତୁ m∠OBC = m∠OCB = 58° (∵ OB = OC)
⇒ x = 58°
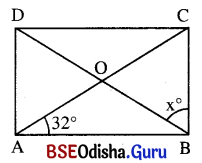
ବର୍ଗଚିତ୍ର:
m∠DOC = m∠POB = 85° କିନ୍ତୁ m∠OBP = 45°
Δ APB ରେ m∠POB + m∠OBP = m∠OPA
⇒ 85° + 45° = x
⇒ x = 130°
![]()
Question 3.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(a) ________ ର କର୍ଣ୍ଣଦ୍ଵୟ ସର୍ବସମ ଏବଂ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ।
ସମାଧାନ:
ବର୍ଗଚିତ୍ର
(b) ABCD ଚତୁର୍ଭୁଜରେ ∠A ଓ ∠B ପରସ୍ପର ପରିପୂରକ ହେଲେ, ଚତୁର୍ଭୁଜଟି ________ ।
ସମାଧାନ:
ଟ୍ରାପିଜିୟମ୍
(c) ଗୋଟିଏ ରମ୍ବସ୍ର କଣ୍ଠଦ୍ଵୟ ସର୍ବସମ ହେଲେ, ରମ୍ବସ୍ ________ ।
ସମାଧାନ:
ବର୍ଗଚିତ୍ର
(d) ABCD ଚତୁର୍ଭୁଜର AB = CD, A͞B || C͞D ହେଲେ, ଚତୁର୍ଭୁଜଟି ________ ।
ସମାଧାନ:
ସାମାନ୍ତରିକ ଚିତ୍ର
(e) ABCD ଚତୁର୍ଭୁଜର AB = BC ଏବଂ AC = BD ଏବଂ ∠B ଏକ ସମକୋଣ ହେଲେ ଚତୁର୍ଭୁଜଟି ________ ।
ସମାଧାନ:
ବର୍ଗଚିତ୍ର
(f) ଗୋଟିଏ ରମ୍ବସ୍ର ଗୋଟିଏ କୋଣର ପରିମାଣ 90° ହେଲେ ରମ୍ବସ୍ ________ ।
ସମାଧାନ:
ବର୍ଗଚିତ୍ର
(g) ABCD ଚତୁର୍ଭୁଜର A͞C ଓ B͞D କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମସ୍ଵିଖଣ୍ଡ କରନ୍ତି ଏବଂ m∠A = 90° ହେଲେ, ଚତୁର୍ଭୁଜଟି ________ ।
ସମାଧାନ:
ଅ।ୟତଚିତ୍ର
(h) ABCD ଚତୁର୍ଭୁଜର A͞C ଓ B͞D କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ୱିଖଣ୍ଡ କରନ୍ତି ଏବଂ AC ≅ BD ହେଲେ, ଚତୁର୍ଭୁଜଟି ________ ।
ସମାଧାନ:
ଅ।ୟତଚିତ୍ର
Question 4.
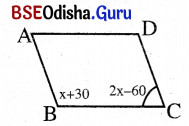
(i) ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ m∠B = (x + 30°) 3 m∠C = (2x – 60°) ହେଲେ m∠A କେତେ ?
ସମାଧାନ:
ଦତ୍ତ : ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ରରେ m∠B = (x + 30°), m∠C = (2x – 60°) ।
ନିର୍ଦେୟ : m∠A ର ପରିମାଣ
ଉତ୍ତର : ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ m∠B+ m∠C = 180°
⇒ (x + 30) + (2x – 60) = 180°
⇒ 3x – 30° = 180°
⇒ 3x = 210°
⇒ x = 70°
∴ m∠A = m∠C = 2x – 60° = 2 × 70° – 60° = 80°
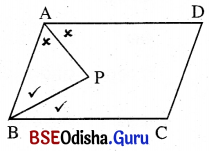
(ii) ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । ∠A ଓ ∠B ର ସମଦ୍ଵିଖଣ୍ଡକଦ୍ବୟ ପରସ୍ପରକୁ P ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । ∠APB ର ପରିମାଣ କେତେ ?
ସମାଧାନ:
ଦତ୍ତ : ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । ∠A ଓ ∠B ର ସମଦ୍ଵିଖଣ୍ଡକ ଯଥାକ୍ରମେ \(\overrightarrow{\mathrm{AP}}\) ଓ \(\overrightarrow{\mathrm{BP}}\)
ପରସ୍ପରକୁ P ବିନ୍ଦୁରେ ଛେଦ କରୁଛନ୍ତି ।
ନିର୍ମେୟ : ∠APB ର ପରିମାଣ ।
ଡତ୍ତର : m∠A + m∠B = 180°
⇒ \(\frac{1}{2}\) m∠A + \(\frac{1}{2}\) m∠B = \(\frac{1}{2}\) × 180°
⇒ m∠PAB + m∠PBA = 90°
Δ APB ରେ m∠PAB + m∠PBA + m∠APB = 180°
[ସାମାନ୍ତରିକ ଚିତ୍ରର ଦୁଇ ସନ୍ନିହିତ କୋଣଦ୍ଵୟର ପରିମାଣର ସମଷ୍ଟି 180° ।]
⇒ 90° + m∠APB = 180°
(∵ m∠PAB + m∠PBA = 90°)
⇒ m∠APB = 180° – 90° = 90°
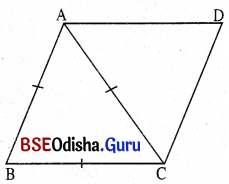
(iii) ଗୋଟିଏ ରମ୍ବସର କ୍ଷୁଦ୍ରତର କର୍ପୂର ଦୈର୍ଘ୍ୟ, ଏହାର ଏକ ବାହୁର ଦୈର୍ଘ୍ୟ ସହ ସମାନ ହେଲେ, ରମ୍ବସ୍ର ବୃହତ୍ତର କୋଣର ପରିମାଣ କେତେ ?
ସମାଧାନ:
ଦତ୍ତ : ABCD ଏକ ରମ୍ବସ୍ରେ A͞C କ୍ଷୁଦ୍ରତର କର୍ଣ୍ଣ ଓ BC = AC ।
ନିଶ୍ଚେୟ : ∠BCD ର ପରିମାଣ ।
ଉତ୍ତର : ABCD ରମ୍ବସ୍ରେ AB = BC । କିନ୍ତୁ BC= AC (ଦତ୍ତ)
∴ AB = BC = AC
⇒ Δ ABC ସମବାହୁ
⇒ m∠ACB = 60°
ସେହିପରି Δ ACD ସମବାହୁ
⇒ m ∠ACD = 60°
∴ m∠BCD=m∠ACB + m∠ACD = 60° + 60° = 120°
(iv) ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ରର ଦୁଇଟି କ୍ରମିକ ଶୀର୍ଷରେ ଉତ୍ପନ୍ନ କୋଣମାନଙ୍କର ପରିମାଣର ଅନୁପାତ 2 : 3 ହେଲେ, ବୃହତ୍ତର କୋଣର ପରିମାଣ କେତେ ?
ସମାଧାନ:
ସାମାନ୍ତରିକ ଚିତ୍ରର ଦୁଇଟି କ୍ରମିକ ଶୀର୍ଷରେ ଉତ୍ପନ୍ନ କୋଣମାନଙ୍କର ପରିମାଣର ଅନୁପାତ 2 : 3 ।
ଦତ୍ତ : ବୃହତ୍ତର କୋଣର ପରିମାଣ ।
ନିଶ୍ଚେୟ : ମନେକର କୋଣଦ୍ଵୟର ପରିମାଣ 2x ଏବଂ 3x ।
ଉତ୍ତର : ସାମାନ୍ତରିକ ଚିତ୍ରରେ 2x + 3x = 180°
[ସାମାନ୍ତରିକ ଚିତ୍ରର ଦୁଇ ସନ୍ନିହିତ କୋଣଦ୍ଵୟର ପରିମାଣର ସମଷ୍ଟି 180° ।]
ସାମାନ୍ତରିକ ଚିତ୍ରରେ 2x + 3x = 180°
⇒ 5x = 180°
⇒ x = 36°
∴ ବୃହତ୍ତମ କୋଣର ପରିମାଣ = 3x = 3 x 36° = 108°
(v) ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ରର ଗୋଟିଏ କୋଣର ପରିମାଣ ଏହାର ଏକ ସନ୍ନିହିତ କୋଣର \(\frac{4}{5}\) ହେଲେ, ସନ୍ନିହିତ କୋଣର ପରିମାଣ ସ୍ଥିର କର ।
ସମାଧାନ:
ଦତ୍ତ : ସାମାନ୍ତରିକ ଚିତ୍ରର ଗୋଟିଏ କୋଣର ପରିମାଣ ଅନ୍ୟ ସନ୍ନିହିତ କୋଣର ପରିମାଣ \(\frac{4}{5}\) ଅଂଶ ।
ନିଶ୍ଚେୟ : ସନ୍ନିହିତ କୋଣଦ୍ଵୟର ପରିମାଣ ।
ଉତ୍ତର : ମନେକର ସନ୍ନିହିତ କୋଣଦ୍ୱୟର ପରିମାଣ x ଏବଂ \(\frac{4 \mathrm{x}^{\circ}}{5}\) ।
ସାମାନ୍ତରିକ ଚିତ୍ରରେ ସନ୍ନିହିତ କୋଣଦ୍ୱୟର ପରିମାଣର ସମଷ୍ଟି 180° ।
x + \(\frac{4 \mathrm{x}^{\circ}}{5}\) = 180°
⇒ 5x + 4x = 900
⇒ 9x = 900
⇒ x = 100
∴ ଗୋଟିଏ କୋଣର ପରିମାଣ 100 ଏବଂ ଅନ୍ୟ ସନ୍ନିହିତ କୋଣର ପରିମାଣ = 180° – 100° = 80° ।
![]()
Question 5.
(i) ABCD ଏକ ଉତ୍ତଳ ଚତୁର୍ଭୁଜ । ଏଥିରେ ∠B, ∠C, ∠D ର ପରିମାଣ ଯଥାକ୍ରମେ ∠A ର ପରିମାଣର ଦୁଇଗୁଣ, ତିନିଗୁଣ, ଚାରିଗୁଣ ହେଲେ ଦର୍ଶାଅ ଯେ, ଏହା ଏକ ଟ୍ରାପିଜିୟମ୍ ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଏକ ଚତୁର୍ଭୁଜ । m∠B = 2m∠A, m∠C = 3m∠A ଏବଂ m∠D = 4m∠A
ପ୍ରାମାଣ୍ୟ : ABCD ଏକ ଟ୍ରାପିଜିୟମ୍ ।
ପ୍ରମାଣ : ମନେକର m∠A = x ତେବେ m∠B = 2x, m∠C = 3x ଏବଂ m∠D = 4x
ABCD ଟ୍ରାପିଜିମ୍ବସ୍ରେ m∠A + m∠B + m∠C + m∠D = 360°
⇒ x + 2x + 3x + 4x = 360°
⇒ 10x = 360°
⇒ x = 36°
∴ m∠A = 36°, m∠B = 2 x 36° = 72°,
m∠C = 3 × 36° = 108° ଏବଂ m∠D = 4 × 36° = 144°
ଲଷ୍ୟକର ଏଠାରେ m∠B + m∠C = 72° + 108° = 180°
∴ A͞B || D͞C
⇒ ABCD ଏକ ଟ୍ରାପିଜିୟମ୍ । (ପ୍ରମାଣିତ)
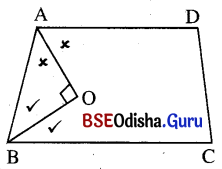
(ii) ABCD ଚତୁର୍ଭୁଜରେ ∠A ଓ ∠B ର ସମତ୍ତିଖଣ୍ଡକ ପରସ୍ପରକୁ ‘O’ ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ଏବଂ ∠AOB ଏକ ସମକୋଣ ହେଲେ ପ୍ରମାଣ କର ଯେ, ABCD ଏକ ଟ୍ରାପିଜିୟମ୍ ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଚତୁର୍ଭୁଜରେ ∠A ଓ ∠B ର ସମଦ୍ବିଖଣ୍ଡକ ପରସ୍ପରକୁ ‘O’ ବିନ୍ଦୁରେ ଛେଦ କରୁଛନ୍ତି ।
m∠AOB = 90°
ପ୍ରାମାଣ୍ୟ : ABCD ଏକ ଟ୍ରାପିଜିୟମ୍ ।
ପ୍ରମାଣ : Δ AOB ରେ m∠OAB + m∠ABO + m∠AOB = 180°
⇒ m∠OAB + m∠ABO = 90°
[∵ m∠AOB = 90° (ଦତ୍ତ)]
⇒ 2m∠OAB + 2m∠ABO = 2 × 90°
⇒ m∠A + m∠B = 180°
⇒ A͞D || B͞C
⇒ ABCD ଏକ ଟ୍ରାପିଜିୟମ୍ ।
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
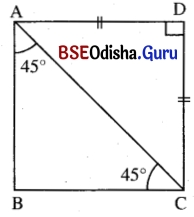
(iii) ABCD ଚତୁର୍ଭୁଜରେ ∠ADC ଏକ ସମକୋଣ, m∠BAC = m∠ACB = 45° ଏବଂ AD = DC ହେଲେ ପ୍ରମାଣ କରି ଯେ, ଏହା ଏକ ବର୍ଗଚିତ୍ର ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ତୁର୍ଭୁଜରେ m∠ADC = 90°, AD = DC, m∠BAC = m∠ACB = 45° ।
ପ୍ରାମାଣ୍ୟ : ABCD ଏକ ଟ୍ରାପିଜିୟମ୍ ।
ପ୍ରମାଣ : Δ ADC ରେ m∠ADC = 90° ଏବଂ AD = DC
⇒ m∠DAC = m∠DCA => m∠DAC = m∠DCA = 45°
Δ ADC ଓ Δ ABC ଦ୍ଠୟରେ m∠DAC = m∠BAC
m∠DCA = m∠ACB ଏବଂ A͞C ସାଧାରଣ ।
∴ Δ ADC ≅ Δ ABC
⇒ AD = AB ଏବଂ DC = BC କିନ୍ତୁ ଦତ୍ତ AD = DC
∴ AD = AB = DC = BC
⇒ ABCD ଏକ ବର୍ଗଚିତ୍ର । (∵ m∠D = 90°)
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
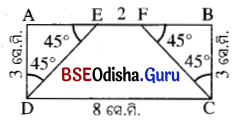
(iv) ABCD ଚତୁର୍ଭୁଜରେ AD = BC = 3 ସେ.ମି., CD = 8 ସେ.ମି. । AB ୟପରେ E ଓ F ଦୁଇଟି ବିନ୍ଦୁ,
m∠BCF = m∠BFC = m∠AED = m∠ADE = 45° ହେଲେ ପ୍ରମାଣ କର ଯେ, ABCD ଏକ ଆୟତଚିତ୍ର ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଚତୁର୍ଭୁଜରେ AD = BC = 3 ସେ.ମି., CD = 8 ସେ.ମି., EF = 2 ସେ.ମି. ଏବଂ
m∠BCF = m∠BFC = m∠AED = m∠ADE = 45°
ପ୍ରାମାଣ୍ୟ : ABCD ଏକ ଟ୍ରାପିଜିୟମ୍ ।
ପ୍ରମାଣ : Δ ADE ରେ m∠ADE = m∠AED = 45°
⇒ AD = AE ଏବଂ m∠A = 90°
∴ AE = 3 ସେ.ମି.
ସେହିପରି Δ FBC ରେ m∠B = 90° ଏବଂ BC = BF = 3 ସେ.ମି.
∴ AB = AE + EF + BF = 3 + 2 + 3 = 8 ସେ.ମି.
ଏଠାରେ AD = BC (ଦତ୍ତ)
AB = DC ଏବଂ m∠A = m∠B = 90°
∴ ABCD ଏକ ଆୟତଚିତ୍ର ।
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
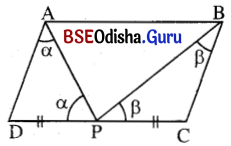
(v) ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । ଯଦି AB = 2AD ଏବଂ P, C͞D ର ମଧ୍ୟବିନ୍ଦୁ ହୁଏ ତେବେ ଦର୍ଶାଅ ଯେ,m∠APB = 90° ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ସାମାନ୍ତରିକ କ୍ଷେତ୍ରରେ AB = 2AD, P, D͞C ର ମଧ୍ୟବିନ୍ଦୁ
ପ୍ରାମାଣ୍ୟ : m∠APB = 90°
ପ୍ରମାଣ : Δ ADP ରେ AD = DP
(∵ 2AD = AB = CD ଏବଂ P, C͞D ର ମଧ୍ୟବିନ୍ଦୁ)
m∠DAP = m∠APD = α (ମନେକର)
ସେହିପରି Δ PBC ରେ PC = BC (∵ AD = BC = DP = PC)
m∠PBC = m∠BPC = β (ମନେକର)
Δ ADP ରେ m∠D =180° – 2α (∵ m∠D + m∠PAD + m∠APD = 180°)
ଓ Δ BPC ରେ m∠C = 180° – 2β
କିନ୍ତୁ m∠D + m∠C = 180° (∵ A͞D || B͞C)
180° – 2α + 180° – 2β = 180°
⇒ 2α + 2β = 180°
⇒ α + β = 90°
m∠APD + m∠BPC = 90°
⇒ m∠APB = 90°
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 6.
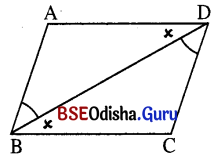
ABCD ଚତୁର୍ଭୁଜରେ m∠ABD = m∠BDC ଏବଂ m∠ADB = m∠CBD ହେଲେ ପ୍ରମାଣ କରି ଯେ, ଏହା ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ଏବଂ Δ ABC = Δ ADC ।
ସମାଧାନ:
ଦତ୍ତ : m∠ABD = m∠BDC ଏବଂ m∠ADB = m∠CBD ।
ପ୍ରାମାଣ୍ୟ : (i) ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
(ii) Δ ABC ≅ Δ ADC
ପ୍ରମାଣ : Δ ABD ଓ Δ BDC ରେ m∠ABD = m∠BDC,
m∠ADB = m∠DBC ଏବଂ B͞D ସାଧାରଣ ବାହୁ
⇒ Δ ABD ≅ Δ ADC ⇒ m∠A = m∠C … (i)
ପୁନଶ୍ଚ, m∠ABD + m∠DBC = m∠BDC + m∠ADB
⇒ m∠B = m∠D … (ii)
(i) ଓ (ii) ରୁ ପାଇଲେ, ABCD ଚତୁର୍ଭୁଜର ବିପରୀତ କୋଣମାନଙ୍କର ପରିମାଣ ସମାନ । ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
∴ ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
![]()
Question 7.
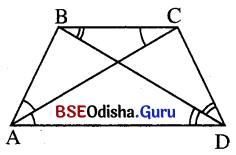
ABCD ଚତୁର୍ଭୁଜରେ BC || AD । A͞C ଓ B͞D ଯଥାକ୍ରମେ ∠BAD ଓ ∠CDA କୁ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରୁଥିଲେ, ପ୍ରମାଣ
କର ଯେ AB = BC = CD ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଚତୁର୍ଭୁଜରେ BC || AD । A͞C ଓ B͞D ଯଥାକ୍ରମେ ∠BAD ଓ ∠CDA କୁ ସମର୍ଦ୍ଦିଖଣ୍ଡ ଜରେ
ପ୍ରାମାଣ୍ୟ : AB = BC = CD
ପ୍ରମାଣ : m∠BAC = m∠CAD (∵ A͞C, ∠BAD ର ସମର୍ଦ୍ଦିଖଣ୍ଡ)
BC || AD
⇒ m∠CAD = m∠BCA (ଏକାନ୍ତର କୋଣ)
⇒ m∠BAC = m∠BCA
⇒ AB = BC … (i)
ସେହିପରି m∠BDC = m∠BDA (ଦତ୍ତ)
BC || AD ⇒ m∠CBD = m∠BDA (ଏକାନ୍ତର କୋଣ)
⇒ m∠BDC = m∠CBD
⇒ BC = CD … (ii)
(i) ଓ (ii) ରୁ ପାଇଲେ, AB = BC = CD
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 8.
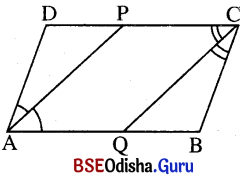
ABCD ସାମାନ୍ତରିକ ଚିତ୍ର । ∠A ଓ ∠C ର ସମଦ୍ବିଖଣ୍ଡକ ଯଥାକ୍ରମେ \(\overrightarrow{\mathrm{AP}}\) ଓ \(\overrightarrow{\mathrm{CQ}}\) । ଏମାନେ ଯଦି D͞C ଓ A͞B କୁ ଯଥାକ୍ରମେ P ଓ Q ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ପ୍ରମାଣ କର ଯେ, APCQ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । ∠A ଓ ∠C ର ସମଦ୍ବିଖଣ୍ଡକ ରଶ୍ମି ଯଥାକ୍ରମେ DC ଓ AB କୁ P ଓ Q ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
ପ୍ରାମାଣ୍ୟ : APCQ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ପ୍ରମାଣ : m∠A = m∠C
⇒ \(\frac{1}{2}\)m∠A = \(\frac{1}{2}\)m∠C
⇒ m∠BCQ = m∠DAP ଏବଂ m∠PCQ = m∠PAQ … (i)
⇒ m∠BCQ + m∠B = m∠DAP + m∠D (∵ m∠B = m∠D)
⇒ m∠AQC = m∠APC … (ii)
(i) ଓ (ii) ରୁ ପାଇବା APCQ ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
(∵ ବିପରୀତ କୋଣମାନଙ୍କର ପରିମାଣ ସମାନ ।)
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 9.
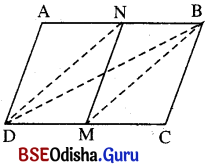
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ M ଓ N ଯଥାକ୍ରମେ D͞C ଓ A͞B ର ମଧ୍ୟବିନ୍ଦୁ । ପ୍ରମାଣ କର ଯେ,
(i) MCBN ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ର
(ii) DMBN ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ର ଏବଂ
(iii) D͞B ଓ M͞N ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ M ଓ N ଯଥାକ୍ରମେ D͞C ଓ A͞B ର ମଧ୍ୟବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : (i) MCBN ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ର ।
(ii) DMBN ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ର ।
(iii) D͞B ଓ M͞N ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି ।
ପ୍ରମାଣ : MCBN ସାମାନ୍ତରିକ ଚିତ୍ରରେ N͞B || M͞C (∵ A͞B || D͞C)
NB = MC (∵ AB = DC ଏବଂ \(\frac{1}{2}\)AB = \(\frac{1}{2}\)DC)
∴ MCBN ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । … (i) (ପ୍ରମାଣିତ)
DMBN ଚିତ୍ରରେ B͞M || D͞N (∵ A͞B || D͞C)
NB = DM (∵ AB = DC ଏବଂ \(\frac{1}{2}\)AB = \(\frac{1}{2}\)DC)
∴ DMBN ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । … (ii) (ପ୍ରମାଣିତ)
DMBN ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ହେତୁ B͞D ଓ N͞M କଣ୍ଠଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରିବେ । … (iii) (ପ୍ରମାଣିତ)
Question 10.
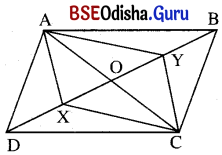
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ A͞C ଓ B͞D କଣ୍ଠଦ୍ଵୟ ପରସ୍ପରକୁ ‘O’ ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । DO ର ମଧ୍ୟବିନ୍ଦୁ X ଓ BO ର ମଧ୍ୟବିନ୍ଦୁ Y ହେଲେ, ପ୍ରମାଣ କର ଯେ AXCY ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ A͞C ଓ B͞D କଣ୍ଠଦ୍ଵୟର ଛେଦବିନ୍ଦୁ ‘O’ । X ଓ Y ଯଥାକ୍ରମେ DO ଏବଂ B͞O ର ମଧ୍ୟବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : AXCY ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ପ୍ରମାଣ : ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
AO = CO ଏବଂ DO = BO
AO = CO ଏବଂ \(\frac{1}{2}\)DO = \(\frac{1}{2}\)BO
AYCX ଏକ ଚତୁର୍ଭୁଜ ଯାହାର କଣ୍ଠଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି ।
AXCY ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 11.
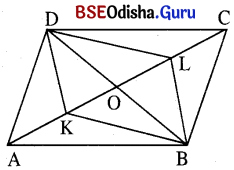
ABCD ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ର । A͞C ଉପରେ K, L ଦୁଇଟି ବିନ୍ଦୁ ଯେପରିକି AK = CL । ପ୍ରମାଣ କର ଯେ, DKBL ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ସାମାନ୍ତରିକ ଚିତ୍ର । A͞C ଉପରେ K, L ଦୁଇଟି ବିନ୍ଦୁ ଯେପରିକି AK = CL ।
ପ୍ରାମାଣ୍ୟ : DKBL ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ଅଙ୍କନ : B͞D ଅଙ୍କନ କର । A͞C ଓ B͞D ର ଛେଦବିନ୍ଦୁ O ହେଉ ।
ପ୍ରମାଣ : ABCD ସାମାନ୍ତରିକ ଚିତ୍ର ।
⇒BO = DO ଏବଂ AO = CO
⇒BO = DO ଏବଂ AO – AK = CO – CL
⇒BO = DO ଏବଂ KO = LO
⇒ DKBL ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
![]()
Question 12.
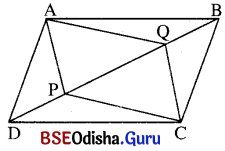
ABCD ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ର । B͞D ଉପରେ P ଓ Q ଦୁଇଟି ବିନ୍ଦୁ ଯେପରିକି AP || CQ । ପ୍ରମାଣ କର ଯେ, DP = BQ ଏବଂ APCQ ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ର । B͞D ଉପରେ P ଓ Q ଦୁଇଟି ବିନ୍ଦୁ ଯେପରିକି A͞P || C͞Q ।
ପ୍ରାମାଣ୍ୟ : (i) DP = BQ
(ii) APCQ ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ପ୍ରମାଣ : A͞P || C͞Q, B͞D ଛେଦକ
∴ m∠APQ = m∠PQC
⇒ m∠APD = m∠BQC … (i)
Δ ADP ଓ Δ BQC ରେ
AD = BC (ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ ବାହୁ)
m∠ADP = m∠QBC, ( AD || BC )
m∠APD = m∠BQC [(i) ରୁ ପ୍ରମାଣିତ]
Δ ADP ≅ Δ BQC
DP = BQ ଏବଂ AP = QC … (ii)
⇒ AP || QC (ଦତ୍ତ) ଏବଂ AP = QC,
⇒ APCQ ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 13.
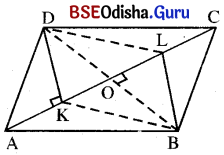
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ DK ⊥ AC, BL ⊥ AC ଏବଂ K ଓ I ଯଥାକ୍ରମେ ଲମ୍ବନ୍ବୟର ପାଦବିନ୍ଦୁ । ପ୍ରମାଣ କର ଯେ, DKBL ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ DK ⊥ AC, BL ⊥ AC ।
ପ୍ରାମାଣ୍ୟ : DKBL ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ଅଙ୍କନ : D͞B ଅଙ୍କନ କର ।
ପ୍ରମାଣ : Δ ADK ଓ Δ BCL ଦ୍ଠୟରେ AD = BC,
ଏବଂ m∠DKA = m∠BLC
Δ ADK ≅ Δ BCL
⇒ AK = CL
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ DO = BO ଏବଂ AO = CO
⇒ DO = BO ଏବଂ AO – AK = CO – CL
⇒ DO = BO ଏବଂ KO = OL
⇒ DKBL ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 14.
ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । A͞D ଉପରେ P ଏକ ବିନ୍ଦୁ ଯେପରିକି DC = DP, \(\overrightarrow{\mathrm{CP}}\) ଓ \(\overrightarrow{\mathrm{BA}}\) ପରସ୍ପରକୁ Q ବିନ୍ଦୁରେ ଛେଦ କରୁଥିଲେ, ପ୍ରମାଣ କର ଯେ
(i) AQ = AP
(ii) BC = BQ
(iii) AD = CD + AQ
ସମାଧାନ:
ଦତ୍ତ : ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । A͞D ଉପରେ P ଏକ ବିନ୍ଦୁ ଯେପରିକି DC = DP । \(\overrightarrow{\mathrm{CP}}\) ଓ \(\overrightarrow{\mathrm{BA}}\) ପରସ୍ପରକୁ Q ।
ପ୍ରାମାଣ୍ୟ : (i) AQ = AP
(ii) BC = BQ
(iii) AD = CD + AQ
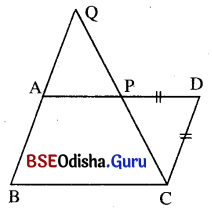
ପ୍ରମାଣ : Δ PCD ରେ DC = DP
m∠DCP = m∠DPC
କିନ୍ତୁ m∠DPC = m∠QPA (ପ୍ରତୀପ)
ଏବଂ m∠DCP = m∠AQP (ଏକାନ୍ତର) (∵ B͞Q || C͞D, Q͞C ଛେଦକ)
m∠DPC = m∠DCP ତେଣ୍ଙ m∠QPA = m∠AQP
⇒ AQ = AP … (i) (ପ୍ରମାଣିତ)
କିନ୍ତୁ m∠DCP = m∠AQP (ଏକାନ୍ତର)
ପୁନଶ୍ଚ, m∠DPC = m∠PCB (ଏକାନ୍ତର)
∠DCP = m∠DPC ତେଣ୍ଙ m∠AQP = m∠PCB
⇒ BC = BQ … (ii) (ପ୍ରମାଣିତ)
ପୂର୍ବ ରୁ ପ୍ରମାଣିତ CD = PD ଏବଂ AQ = AP
CD + AQ = PD + AP
⇒ CD + AQ = AD … (iii) (ପ୍ରମାଣିତ)
![]()
Question 15.
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ D͞C ବାହୁ ଉପରେ X ଏକ ବିନ୍ଦୁ ଯେପରିକି AD = AX । ପ୍ରମାଣ କର ଯେ, m∠XAB = m∠ABC ଏବଂ AC = BX ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । D͞C ଉପରେ X ଏକ ବିନ୍ଦୁ ଯେପରିକି AD = AX ।
ପ୍ରାମାଣ୍ୟ : (i) m∠XAB = m∠ABC
(ii) AC = BX
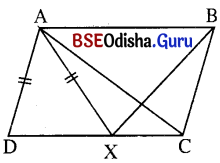
ପ୍ରମାଣ : AD = AX
⇒ m∠ADX = m∠AXD
କିନ୍ତୁ m∠ADX = m∠ABC (ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ କୋଣ)
m∠AXD = m∠XAB (ଏକାନ୍ତର)
∴ m∠XAB = m∠ABC … (i) (∵ m∠ADX = m∠AXD) (ପ୍ରମାଣିତ)
Δ AXB ଓ Δ BAC ଦ୍ଠୟରେ m∠XAB = m∠ABC,
∴ A͞B ସାଧାରଣ ଏବଂ AX = BC (∵ AX = AD = BC)
Δ AXB ≅ Δ BAC
⇒ BX = AC … (ii) (ପ୍ରମାଣିତ)
Question 16.
ପ୍ରମାଣ କର ଯେ, ସାମାନ୍ତରିକ ଚିତ୍ରର କୋଣମାନଙ୍କର ସମଦ୍ବିଖଣ୍ଡକ ରେଖାମାନଙ୍କ ଦ୍ବାରା ଗଠିତ ଚତୁର୍ଭୁଜଟି ଏକ ଅ।ୟତଚିତ୍ର ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । ∠A ଓ ∠B ର ସମଦ୍ଵିଖଣ୍ଡକ ରଶ୍ମିଦ୍ବୟର ଛେଦବିନ୍ଦୁ M, ∠B ଓ ∠C ର
ସମଦ୍ବିଖଣ୍ଡକ ରଶ୍ମିଦ୍ବୟର ଛେଦବିନ୍ଦୁ N, ∠C ଓ ∠D ର ସମଦ୍ବିଖଣ୍ଡକ ରଶ୍ମିଦ୍ବୟର ଛେଦବିନ୍ଦୁ P ଏବଂ ∠D ଓ ∠Aର ସମଦ୍ବିଖଣ୍ଡକ ରଶ୍ମିଦ୍ଵୟର ଛେଦବିନ୍ଦୁ Q ।
ପ୍ରାମାଣ୍ୟ : MNPQ ଏକ ଅ।ୟତଚିତ୍ର ।
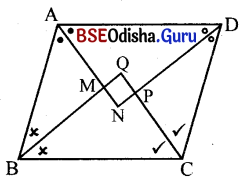
ପ୍ରମାଣ : m∠A + m∠B = 180°
⇒ \(\frac{1}{2}\)m∠A + \(\frac{1}{2}\)m∠B = 180°
⇒ m∠MAB + m∠MBA = 90°
⇒ m∠AMB = 90°
⇒ m∠AMB = m∠QMN = 90° (ପ୍ରତୀପ କୋଣ)
ସେହିପରି ପ୍ରମାଣ କରାଯାଇପାରେ ଯେ, m∠QPN = 90°, m∠MQP= 90° ଏବଂ m∠MNP = 90°
∴ MNPQ ଏକ ଅ।ୟତଚିତ୍ର । (ପ୍ରମାଣିତ)
Question 17.
ପ୍ରମାଣ କର ଯେ, ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ରର କର୍ଣ୍ଣଦ୍ୱୟର ଛେଦବିନ୍ଦୁ ମଧ୍ୟଦେଇ ଅଙ୍କିତ ଓ ସାମାନ୍ତରିକ ଚିତ୍ରର ବାହୁମାନଙ୍କ ଦ୍ଵାରା ସୀମାବଦ୍ଧ ରେଖାଖଣ୍ଡ କର୍ତ୍ତୃମାନଙ୍କ ଛେଦବିନ୍ଦୁଠାରେ ସମଦ୍ବିଖଣ୍ଡିତ ହୁଏ ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ରରେ A͞C ଓ B͞D କର୍ଣ୍ଣଦ୍ୱୟର ଛେଦବିନ୍ଦୁ O।
O ବିନ୍ଦୁ ଦେଇ ଅଙ୍କିତ ଏକ ରେଖା A͞B ଓ CD କୁ M ଓ N ବିନ୍ଦୁରେ ଛେଦକରୁଛି ।
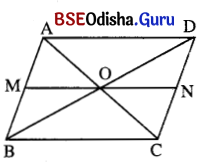
ପ୍ରାମାଣ୍ୟ : MO = ON
ପ୍ରମାଣ : Δ BMO ଏବଂ Δ DNO ଦ୍ବୟରେ
m∠MOB = m∠NOD (ପ୍ରତୀପ)
m∠MBO = m∠NDO (ଏକାନ୍ତର),
BO = CO (ସାମାନ୍ତରିକ ଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି)
∴ Δ BMO ≅ Δ DNO (∵ କୋ-ବା-କୋ ସର୍ବସମତା)
⇒ MO = ON (ପ୍ରମାଣିତ)
![]()
Question 18.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ R͞P || A͞B, RQ || BC ଏବଂ PQ || AC ହେଲେ ଦର୍ଶାଅ ଯେ BC = \(\frac{1}{2}\)QR ।
ସମାଧାନ:
ଦତ୍ତ : ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ RP || AB, RQ || BC ଏବଂ PQ || AC ।
ପ୍ରାମାଣ୍ୟ : BC = \(\frac{1}{2}\)QR
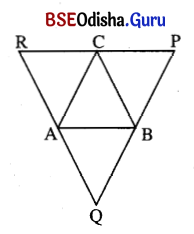
ପ୍ରମାଣ : RQ || BC, RP || AB
⇒ RABC ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର
⇒ BC = RA
ସେହିପରି RQ || BC, PQ || AC
⇒ AQBC ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର
⇒ BC = AQ
⇒ 2BC = RA + AQ
⇒ 2BC = RQ
⇒ BC = \(\frac{1}{2}\)QR (ପ୍ରମାଣିତ)
