BSE Odisha 9th Class Maths Solutions Geometry Chapter 3 ଚତୁର୍ଭୁଜ Ex 3(c)

Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 3 ଚତୁର୍ଭୁଜ Ex 3(c) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Geometry Chapter 3 ଚତୁର୍ଭୁଜ Ex 3(c)

Question 1.
ନିମ୍ନ ଚିତ୍ରରେ L₁ || L₂ || L₃ || L₄, \(\overleftrightarrow{\mathbf{A D}}\) || \(\overleftrightarrow{\mathbf{P S}}\) ଓ AB = BC = CD ।
(a) ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

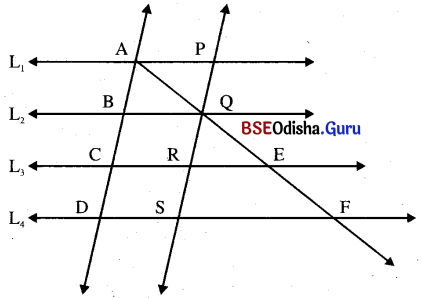
(i) AQ = _______ = _______
ସମାଧାନ:
AQ = QE = EF

(ii) PQ = \(\frac{1}{3}\) ( _______ )
ସମାଧାନ:
PQ = \(\frac{1}{3}\) PS

(iii) EF = \(\frac{1}{3}\) ( _______ )
ସମାଧାନ:
EF = \(\frac{1}{3}\) AF

(iv) BQ = \(\frac{1}{2}\) ( _______ )
ସମାଧାନ:
BQ = \(\frac{1}{2}\) CE

(v) RE = \(\frac{1}{2}\) ( _______ )
ସମାଧାନ:
RE = \(\frac{1}{2}\) SF

(b) ନିମ୍ନଲିଖ୍ତ ଉକ୍ତିମାନଙ୍କ ମଧ୍ୟରୁ ଭୁଲ୍ ଓ ଠିକ୍ ଉକ୍ତିଗୁଡ଼ିକୁ ଦର୍ଶାଅ ।
(i) AQ = \(\frac{1}{2}\)AE
ସମାଧାନ:
ଠିକ୍ ଉକ୍ତି

(ii) BQ = \(\frac{1}{2}\)DF
ସମାଧାନ:
ଭୁଲ୍ ଉକ୍ତି

(iii) AF = 2AQ
ସମାଧାନ:
ଭୁଲ୍ ଉକ୍ତି

(iv) AP = DS
ସମାଧାନ:
ଠିକ୍ ଉକ୍ତି

(v) RE = \(\frac{1}{2}\)SF
ସମାଧାନ:
ଠିକ୍ ଉକ୍ତି

(vi) 3QE = AF
ସମାଧାନ:
ଠିକ୍ ଉକ୍ତି

Question 2.
ପାର୍ଶ୍ୱ ସ୍ଥ ଚିତ୍ରରେ FG || DE || BC ଏବଂ AB ର ମଧ୍ୟବିନ୍ଦୁ D, AD ର ମଧ୍ୟବିନ୍ଦୁ F ହେଲେ ନିମ୍ନ ଅନୁପାତଗୁଡ଼ିକ ସ୍ଥିର କର ।

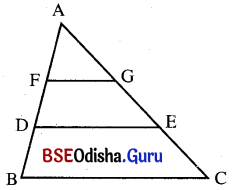
(i) AG : GE
ସମାଧାନ:
1 : 1

(ii) AG : GC
ସମାଧାନ:
1 : 3

(iii) GE : EC
ସମାଧାନ:
1 : 2

(iv) AG : AC
ସମାଧାନ:
1 : 4

(v) GE : AC
ସମାଧାନ:
1 : 4

(vi) EC : AC
ସମାଧାନ:
1 : 2

Question 3.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(a) ଗୋଟିଏ ଚତୁର୍ଭୁଜର ବାହୁମାନଙ୍କର ମଧ୍ୟବିନ୍ଦୁକୁ କ୍ରମାନ୍ୱୟରେ ଯୋଗକଲେ, ଉତ୍ପନ୍ନ ଚତୁର୍ଭୁଜଟି __________ ହେବ ।
ସମାଧାନ:
ସାମାନ୍ତରିକ ଚିତ୍ର

(b) ଗୋଟିଏ ଅ‍।ୟତଚିତ୍ର ବାହୁମାନଙ୍କର ମଧ୍ୟବିନ୍ଦୁକୁ କ୍ରମାନ୍ୱୟରେ ଯୋଗକଲେ, ଉତ୍ପନ୍ନ ଚତୁର୍ଭୁଜଟି __________ ହେବ ।
ସମାଧାନ:
ରମ୍ବସ୍

(c) ଗୋଟିଏ ଆୟତଚିତ୍ରର ବାହୁମାନଙ୍କର ମଧ୍ୟବିନ୍ଦୁକୁ କ୍ରମାନ୍ୱୟରେ ଯୋଗକଲେ, ଉତ୍ପନ୍ନ ଚତୁର୍ଭୁଜଟି __________ ହେବ ।
ସମାଧାନ:
ବର୍ଗଚିତ୍ର

(d) ଗୋଟିଏ ବର୍ଗଚିତ୍ରର ବାହୁମାନଙ୍କର ମଧ୍ୟବିନ୍ଦୁକୁ କ୍ରମାନ୍ୱୟରେ ଯୋଗକଲେ, ଉତ୍ପନ୍ନ ଚତୁର୍ଭୁଜଟି __________ ହେବ ।
ସମାଧାନ:
ଅ‍।ୟତଚିତ୍ର

(e) ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ରର ବାହୁମାନଙ୍କର ମଧ୍ୟବିନ୍ଦୁକୁ କ୍ରମାନ୍ୱୟରେ ଯୋଗକଲେ, ଉତ୍ପନ୍ନ ଚତୁର୍ଭୁଜଟି __________ ହେବ ।
ସମାଧାନ:
ସାମାନ୍ତରିକ ଚିତ୍ର

Question 4.
ଏକ ସମବାହୁ Δ ABC ର ବାହୁମାନଙ୍କର ମଧ୍ୟବିନ୍ଦୁ D, E ଓ F ହେଲେ, ଦର୍ଶାଅ ଯେ, Δ DEF ସମବାହୁ ।
ସମାଧାନ:
ଦତ୍ତ : ସମବାହୁ Δ ABC ରେ AB = AC = BC ।
D, E ଓ F ଯଥାକ୍ରମେ AB, BC ଓ AC ର ମଧ୍ୟବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : Δ DEF ସମବାହୁ ।

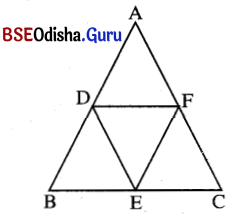
ପ୍ରମାଣ : ABC ରେ A͞B ର ମଧ୍ୟବିନ୍ଦୁ D ଓ A͞C ର ମଧ୍ୟବିନ୍ଦୁ F ।
DF = \(\frac{1}{2}\) BC
ସେହିପରି DE = \(\frac{1}{2}\) BC ଏବଂ EF = \(\frac{1}{2}\) AB
କିନ୍ତୁ AB = BC = AC
⇒ \(\frac{1}{2}\) AB = \(\frac{1}{2}\) BC = \(\frac{1}{2}\) AC
⇒ EF = DF = DE
⇒ Δ DEF ସମବାହୁ । (ପ୍ରମାଣିତ)

Question 5.
ଗୋଟିଏ ତ୍ରିଭୁଜର ବାହୁମାନଙ୍କର ମଧ୍ୟବିନ୍ଦୁଗୁଡ଼ିକୁ ଯୋଗକଲେ ଯେଉଁ ଚାରିଗୋଟି ତ୍ରିଭୁଜ ଉତ୍ପନ୍ନ ହୁଏ, ସେମାନେ ସର୍ବସମ ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ D, E ଓ F ଯଥାକ୍ରମେ A͞B, B͞C ଓ A͞C ର ମଧ୍ୟବିନ୍ଦୁ ।
D, E ଓ F କୁ କ୍ରମାନ୍ୱୟରେ ଯୋଗକଲେ ଚାରିଗୋଟି ତ୍ରିଭୁଜ ଉତ୍ପନ୍ନ ହେଉଛି ।
ପ୍ରାମାଣ୍ୟ : Δ DEF ≅ Δ ADF ≅ Δ BED ≅ Δ ECF
ପ୍ରମାଣ : Δ ABC ର A͞B ଓ AC ର ମଧ୍ୟବିନ୍ଦୁ ଯଥାକ୍ରମେ D ଓ F ।

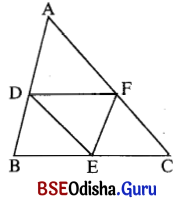
⇒ DF || BC
⇒ DF || BE
ସେହିପରି ପ୍ରମାଣ କରାଯାଇପାରେ ଯେ, EF || AB
⇒ EF || BD
BDFE ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ଏହାର D͞E କଣ୍ଠ ସାମାନ୍ତରିକ ଚିତ୍ରକୁ ଦୁଇଟି ସର୍ବସମ ତ୍ରିଭୁଜରେ ପରିଣତ କରେ
∴ Δ BDE ≅ Δ DEF
ସେହିପରି ପ୍ରମାଣ କରାଯାଇ ପାରେ ଯେ, Δ DEF ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ଏବଂ Δ ADF ≅ Δ DEF ।
ପୁନଣ୍ଚ, DECF ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ଏବଂ Δ CEF ≅ Δ DEF
∴ Δ DEF ≅ Δ ADF ≅ Δ BDE ≅ Δ CEF

Question 6.
ଚିତ୍ରରେ ABCD ଏକ ଟ୍ରାପିଜିୟମ୍ । D͞C || A͞B; E, AD ର ମଧ୍ୟବିନ୍ଦୁ । EF || AB ହେଲେ ଦର୍ଶାଅ ଯେ F, B͞C ର ମଧ୍ୟବିନ୍ଦୁ ।
ସମାଧାନ:

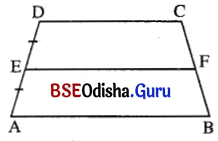
ଦତ୍ତ : ABCD ଟ୍ରାପିଜିୟମ୍‌ରେ DC || EF || AB ଏବଂ E, AD ର ମଧ୍ୟବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : F, B͞C ର ମଧ୍ୟବିନ୍ଦୁ ଅର୍ଥାତ୍ CF = FB ।
ପ୍ରମାଣ : DC || EF || AB, DA ଓ B͞C ଦୁଇ ଛେଦକ ।
DA ଛେଦକର ଛେଦିତ ଅଂଶମାନ ସମାନ, ଅର୍ଥାତ୍ DE = EA 
∴ ଅନ୍ୟ ଛେଦକ B͞C ର ଛେଦିତ ଅଂଶମାନ ସମାନ ହେବେ, ଅର୍ଥାତ୍ CF = FB
⇒ F, BC ର ମଧ୍ୟବିନ୍ଦୁ । (ପ୍ରମାଣିତ)

Question 7.
ଚିତ୍ରରେ AD ⊥ l ଏବଂ BE ⊥ l, C, A͞B ର ମଧ୍ୟବିନ୍ଦୁ ହେଲେ, CD = CE ।

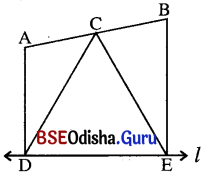
ସମାଧାନ:
ଦତ୍ତ : l ରେଖା ଉପରେ AD ଓ BE ଲମ୍ବ । A͞B ର ମଧ୍ୟବିନ୍ଦୁ C ।

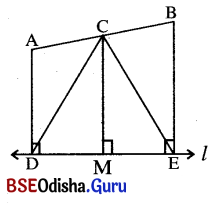
ପ୍ରାମାଣ୍ୟ : CD = CE
ଅଙ୍କନ : C͞M ⊥ l ଅଙ୍କନ କର ।
ପ୍ରମାଣ : AD || CM || BE (∵ AD, CM ଏବଂ B͞E ପ୍ରତ୍ୟେକ l ପ୍ରତି ଲମ୍ବ)
ଏବଂ AC = CB (∵ C, A͞B ର ମଧ୍ୟବିନ୍ଦୁ)
∴ M, D͞E ର ମଧ୍ୟବିନ୍ଦୁ ।
Δ CDE ରେ C͞M, D͞E ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ ।
⇒ Δ CDE ସମଦ୍ବିବାହୁ ।
⇒ CD = CE (ପ୍ରମାଣିତ)

Question 8.
Δ ABC ରେ M ଓ N, A͞B ବାହୁକୁ ସମତ୍ରିଖଣ୍ଡ କରନ୍ତି । M͞P ଓ NQ ପ୍ରତ୍ୟେକ B͞C ସହ ସମାନ୍ତର ଏବଂ ସେମାନେ 
A͞C କୁ ଯଥାକ୍ରମେ P ଓ ଠୁ ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । ପ୍ରମାଣ କର ଯେ, P ଏବଂ Q, AC କୁ ସମତ୍ରିଖଣ୍ଡ କରିବେ ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ର A͞B ଉପରେ M ଓ N ଏପରି ଦୁଇଟି ବିନ୍ଦୁ ଯେପରିକି 
AM = MN = NB ଏବଂ MP || NQ || BC ।

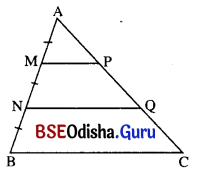
ପ୍ରାମାଣ୍ୟ : AP = PQ = QC
ପ୍ରମାଣ : MP || NQ || BC ଏବଂ A͞B ଓ A͞C ଏମାନଙ୍କର ଦୁଇଟି ଛେଦକ । 
A͞B ଛେଦକର ଛେଦିତ ଅଂଶମାନ ସର୍ବସମ । ଅର୍ଥାତ୍ AM = MN = NB 
AP = PQ = QC (A͞C ଛେଦକର ଛେଦିତ ଅଂଶମାନ ସର୍ବସମ ହେବେ ।) (ପ୍ରମାଣିତ)

Question 9.
Δ ABC ରେ M, P ଓ Q ଯଥାକ୍ରମେ BC, AB ଓ AC ର ମଧ୍ୟବିନ୍ଦୁ ଏବଂ P͞Q ଓ A͞M ର ଛେଦବିନ୍ଦୁ R । ପ୍ରମାଣ କର ଯେ,
AR = RM, PR = RQ ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ M, P ଓ Q ଯଥାକ୍ରମେ BC, AB ଓ A͞C ର ମଧ୍ୟବିନ୍ଦୁ ।  
PQ ଓ A͞M ଦ୍ବୟ ପରସ୍ପରକୁ R ବିନ୍ଦୁରେ ଛେଦ କରୁଛନ୍ତି ।
ପ୍ରାମାଣ୍ୟ : AR = RM ଏବଂ PR = RQ 
ଅର୍ଥାତ୍ A͞M ଓ PQ ପରସ୍ପରକୁ 
R ବିନ୍ଦୁରେ ସମଦ୍ବିଖଣ୍ଡ କରିବେ ।

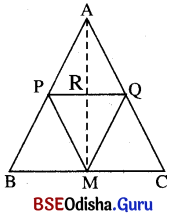
ପ୍ରମାଣ : QM || AB ଏବଂ PM || AC
⇒ APMQ ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । 
∴ ଏହାର କଣ୍ଠଦ୍ଵୟ A͞M ଓ PQ
ପରସ୍ପରକୁ R ବିନ୍ଦୁରେ ସମଦ୍ବିଖଣ୍ଡ କରିବେ । (ପ୍ରମାଣିତ)

Question 10.
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ X ଓ Y ଯଥାକ୍ରମେ A͞D ଓ B͞C ର ମଧ୍ୟବିନ୍ଦୁ । C͞X ଓ A͞Y, B͞D କୁ ଯଥାକ୍ରମେ P ଓ Q ବିନ୍ଦୁରେ ଛେଦକଲେ ପ୍ରମାଣ କର ଯେ, DP = PQ = QB । 
ସମାଧାନ:
ଦତ୍ତ : ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ X ଓ Y ଯଥାକ୍ରମେ A͞D ଓ B͞C ର ମଧ୍ୟବିନ୍ଦୁ । C͞X ଓ A͞Y, B͞D କୁ ଯଥାକ୍ରମେ P ଓ Q ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
ପ୍ରାମାଣ୍ୟ : DP = PQ = BQ
ପ୍ରମାଣ : X, AD ର ମଧ୍ୟବିନ୍ଦୁ ⇒ AX = XD

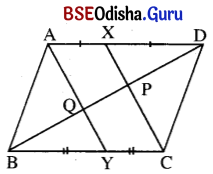
Y, B͞C ର ମଧ୍ୟବିନ୍ଦୁ ⇒ BY = CY
∴ AD = BC ⇒ \(\frac{1}{2}\)AD = \(\frac{1}{2}\)BC
⇒ AX = CY
ପୁନଣ୍ଚ A͞D || B͞C ⇒ AX || CY
∴ AXCY ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । ⇒ XC || AY
Δ ADQ ରେ X, A͞D ର ମଧ୍ୟବିନ୍ଦୁ ଏବଂ X͞P || A͞Q
⇒ P, D͞Q ର ମଧ୍ୟବିନ୍ଦୁ ⇒ DP = PQ … (i)
ସେହିପରି Δ BPC ରେ Y, B͞C ର ମଧ୍ୟବିନ୍ଦୁ ଏବଂ Q͞Y || P͞C
⇒ Q, BP ର ମଧ୍ୟବିନ୍ଦୁ ⇒ BQ = PQ ... (ii)
(i) ଓ (ii) ରୁ DP = PQ = BQ (ପ୍ରମାଣିତ)

Question 11.
Δ ABC ରେ A͞M ମଧ୍ଯମାର ମଧ୍ୟବିନ୍ଦୁ R । \(\overrightarrow{\mathrm{BR}}\) ଓ A͞C ପରସ୍ପରକୁ S ବିନ୍ଦୁରେ ଛେଦ କରୁଥିଲେ, ପ୍ରମାଣ କର ଯେ
AS= \(\frac{1}{3}\) AC ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ A͞M ମଧ୍ଯମାର ମଧ୍ୟବିନ୍ଦୁ R । \(\overrightarrow{\mathrm{BR}}\) ଓ A͞C ପରସ୍ପରକୁ S ।
ପ୍ରାମାଣ୍ୟ : AS= \(\frac{1}{3}\) AC

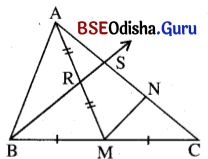
ଅଙ୍କନ : M ବିନ୍ଦୁରୁ BS ସହ ସମାନ୍ତର କରି M͞N ଅଙ୍କନ କର ଯାହା A͞C କୁ N ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
ପ୍ରମାଣ : Δ AMN ରେ R, A͞M ର ମଧ୍ୟବିନ୍ଦୁ ଏବଂ RS || MN (ଅଙ୍କନ) ।
⇒ S, AN ର ମଧ୍ୟବିନ୍ଦୁ
⇒ AS = SN
ପୁନଶ୍ଚ, Δ CBS ରେ M, BC ର ମଧ୍ୟବିନ୍ଦୁ ଏବଂ M͞N || B͞S ।
⇒ N, SC ର ମଧ୍ୟବିନ୍ଦୁ
⇒ SN = NC
∴ AS = SN = NC ⇒ AS = \(\frac{1}{3}\) AC (ପ୍ରମାଣିତ)

Question 12.
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ B͞C ର ମଧ୍ୟବିନ୍ଦୁ P। \(\overrightarrow{\mathrm{DP}}\) ଓ \(\overrightarrow{\mathrm{AB}}\) ପରସ୍ପରକୁ Q ବିନ୍ଦୁରେ ଛେଦକଲେ, ପ୍ରମାଣ କର ଯେ,
AQ = 2AB ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ B͞C ର ମଧ୍ୟବିନ୍ଦୁ P। \(\overrightarrow{\mathrm{DP}}\) ଓ \(\overrightarrow{\mathrm{AB}}\) ପରସ୍ପରକୁ Q ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
ପ୍ରାମାଣ୍ୟ : AQ = 2AB
ପ୍ରମାଣ : Δ BQP ଓ Δ DPC ଦ୍ଠୟରେ BP = PC

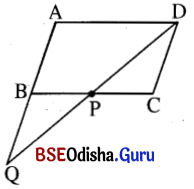
m∠BPQ = m∠CPD (ପ୍ରତୀପ)
ଏବଂ m∠PBQ = m∠PCQ (ଏକାନ୍ତର)
Δ BQP ≅ Δ DPC
⇒ PQ = PD
⇒ P, DQ ର ମଧ୍ୟବିନ୍ଦୁ
Δ AQD ରେ P, DQ ର ମଧ୍ୟବିନ୍ଦୁ ଏବଂ BP || AD
B, AQ ର ମଧ୍ୟବିନ୍ଦୁ
⇒ AB = BQ
⇒ 2AB = AQ

Question 13.
Δ ABC ରେ CM, AB କୁ M ଚିତ୍ରରେ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରେ ଓ B͞Q, C͞M କୁ P ଚିତ୍ରରେ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରେ । Q, A͞C ଉପରେ ଅବସ୍ଥିତ ହେଲେ, ପ୍ରମାଣ କର ଯେ, AQ = 2QC ।
ସମାଧାନ:
ଦତ୍ତ : AABC ରେ C͞M, A͞B କୁ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରେ । P, M͞C ର ମଧ୍ୟବିନ୍ଦୁ \(\overrightarrow{\mathrm{BP}}\) ଓ A͞C ର ଛେଦବିନ୍ଦୁ Q ।
ପ୍ରାମାଣ୍ୟ : AQ = 2QC
ଅଙ୍କନ : M ବିନ୍ଦୁ ମଧ୍ୟଦେଇ B͞Q ସହ ସମାନ୍ତର କରି M͞N ଅଙ୍କନ କର ଯାହା A͞C କୁ N ବିନ୍ଦୁରେ ଛେଦ କରିବ ।

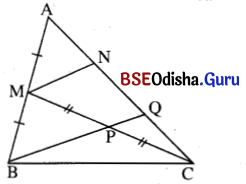
ପ୍ରମାଣ : Δ CMN ରେ P, MC ର ମଧ୍ୟବିନ୍ଦୁ ଏବଂ PQ || MN
⇒ NQ = QC … (i)
Δ ABQ ରେ M, A͞B ର ମଧ୍ୟବିନ୍ଦୁ ଏକ MN || BQ
⇒ AN = NQ … (ii)
(i) ଓ (ii) ରୁ AN = NQ = QC
⇒ AN = NQ = QC + QC
⇒ AQ = 2QC (ପ୍ରମାଣିତ)

Question 14.
ପ୍ରମାଣ କର ଯେ, ଟ୍ରାପିଜିୟମ୍‌ର ଦୁଇ ଅସମାନ୍ତର ବାହୁର ମଧ୍ୟବିନ୍ଦୁଦ୍ଵୟକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡ ସମାନ୍ତର ବାହୁମାନଙ୍କ ସହ ସମାନ୍ତର ଏବଂ ଏହାର ଦୈର୍ଘ୍ୟ ସମାନ୍ତର ବାହୁମାନଙ୍କ ଦୈର୍ଘ୍ୟର ସମଷ୍ଟିର ଅର୍ଦ୍ଧେକ ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଟ୍ରାପିଜିୟମ୍‌ରେ । M ଓ N ଯଥାକ୍ରମେ AD ଓ B͞C ର ମଧ୍ୟବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : MN || DC ଏବଂ MN = \(\frac{1}{2}\) (AB + CD)

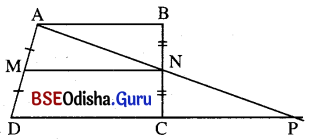
ଅଙ୍କନ : \(\overrightarrow{\mathrm{AN}}\) ଓ \(\overrightarrow{\mathrm{DC}}\) ର ଛେଦବିନ୍ଦୁ P
ପ୍ରମାଣ : Δ ABN ଓ Δ CNP ରେ BN = NC, m∠ANB = m∠CNP (ପ୍ରତୀପ)
ଏବଂ m∠ABN = m∠NCP
∴ Δ ABN ≅ Δ CNP
⇒ AN = NP ଏବଂ AB = CP
ବର୍ତ୍ତମାନ Δ ADP ରେ M ଓ N ଯଥାକ୍ରମେ A͞D ଓ A͞P ର ମଧ୍ୟବିନ୍ଦୁ ।
∴ M͞N || D͞P … (i)
ଏବଂ MN = \(\frac{1}{2}\) DP … (ii)
(i) ରୁ M͞N || D͞P ⇒ MN || DC
(ii) ରୁ MN = \(\frac{1}{2}\) DP = \(\frac{1}{2}\) (DC + DP) = \(\frac{1}{2}\) (DC + AB) [∵ AB = CP]
MN = \(\frac{1}{2}\) (AB + CD) (ପ୍ରମାଣିତ)

Question 15.
Δ ABC ରେ ∠B ସମକୋଣ । AC ର ମଧ୍ୟବିନ୍ଦୁ ‘P’ ହେଲେ ଦର୍ଶାଅ ଯେ, PA = PB = PC ।
ସମାଧାନ:
ଦତ୍ତ : Δ ABC ରେ m∠B = 90° ଏବଂ P, AC ର ମଧ୍ୟବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : PA = PB = PC

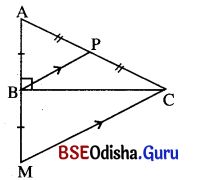
ଅଙ୍କନ : C ବିନ୍ଦୁରେ BP ସହ ସମାନ୍ତର କରି CM ଅଙ୍କନ କର ଯାହା \(\overrightarrow{\mathrm{AM}}\) କୁ M ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
ପ୍ରମାଣ : Δ AMC ରେ P, A͞C ର ମଧ୍ୟବିନ୍ଦୁ ଏବଂ PB || CM ।
⇒ AB = BM ଏବଂ 2BP = MC
ଏଠାରେ C͞B, A͞M ର ସମଦ୍ଵିଖଣ୍ଡକ ଲମ୍ବ ହେଲା ।
⇒ AC = MC
2AP = 2BP ⇒ AP = BP
କିନ୍ତୁ ଦତ୍ତ AP = PC
∴ AP = BP = PC (ପ୍ରମାଣିତ)

ବିକଳ୍ପ ସମାଧାନ :
ଦତ୍ତ : Δ ABC ରେ m∠B = 90° ଏବଂ AC ର ମଧ୍ୟବିନ୍ଦୁ P ।
ପ୍ରାମାଣ୍ୟ : PA = PB = PC

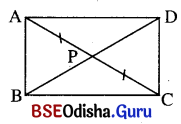
ଅଙ୍କନ : \(\overrightarrow{\mathrm{BP}}\) ଉପରେ D ଏପରି ଏକ ବିନ୍ଦୁ ହେଉ ଯେପରିକି B – P – D ଓ BP = PD ।
QA ଓ QC ଅଙ୍କନ କର ।
ପ୍ରମାଣ : ABCD ଚତୁର୍ଭୁଜରେ BP = PD (ଅଙ୍କନ) ଓ AP = PC (ଦତ୍ତ)
⇒ ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
∠B ସମକୋଣ ହେତୁ ABCD ଏକ ଆୟତଚିତ୍ର ।
⇒ କଣ୍ଠ AC = BD
\(\frac{1}{2}\) AC = \(\frac{1}{2}\) BD
⇒ PA = PB
∴ PA = PB = PC (∵ AP = PC) (ପ୍ରମାଣିତ)

Question 16.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର କଣ୍ଠଦ୍ଵୟର ମଧ୍ୟବିନ୍ଦୁକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡର ଦୈର୍ଘ୍ୟ, ସମାନ୍ତର ବାହୁମାନଙ୍କ ସହ ସମାନ୍ତର ଏବଂ ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଅନ୍ତରର ଅର୍ଦ୍ଧେକ ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଟ୍ରାପିଜିୟମ୍‌ରେ AB || CD । M ଓ N ଯଥାକ୍ରମେ B͞D ଓ A͞C ର ମଧ୍ୟବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : M͞N || D͞C ଏବଂ MN = \(\frac{1}{2}\) (DC – AB)

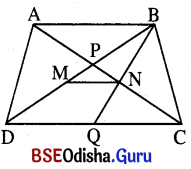
ଅଙ୍କନ : \(\overrightarrow{\mathrm{BN}}\) ଓ D͞C ର ଛେଦବିନ୍ଦୁ Q ଚିହ୍ନଟ କର ।
ପ୍ରମାଣ : Δ ABN ଏବଂ Δ QCN ଦ୍ଠୟରେ
m∠ANB = m∠CNQ (ପ୍ରତୀପ)
AN = NC (∵ N, A͞C ର ମଧ୍ୟବିନ୍ଦୁ)
m∠BAN = m∠NCQ (ଏକାନ୍ତର)
∴ Δ ABN ≅ Δ QCN (କୋ-ବା-କୋ-ସର୍ବସମତା)
⇒ BN = NQ ଏବଂ AB = QC
Δ BDQ ରେ M ଓ N ଯଥାକ୍ରମେ B͞D ଓ B͞Q ର ମଧ୍ୟବିନ୍ଦୁ ।
∴ M͞N || D͞Q ଏବଂ MN = \(\frac{1}{2}\) DQ
M͞N || D͞Q ⇒ MN || DC
ପୁନଶ୍ଚ, MN = \(\frac{1}{2}\) DQ = \(\frac{1}{2}\) (DC – DQ) = \(\frac{1}{2}\) (DC – AB) (∵ AB = QC)
∴ MN = \(\frac{1}{2}\) (DC – AB)  (ପ୍ରମାଣିତ)

Question 17.
ପ୍ରମାଣ କର ଯେ, କୌଣସି ଚତୁର୍ଭୁଜର ବାହୁମାନଙ୍କର ମଧ୍ୟବିନ୍ଦୁଗୁଡ଼ିକୁ ପର୍ଯ୍ୟାୟକ୍ରମେ ଯୋଗକଲେ, ଉତ୍ପନ୍ନ ଚତୁର୍ଭୁଜଟି ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଚତୁର୍ଭୁଜର M, N, P ଓ Q ଯଥାକ୍ରମେ A͞B, A͞D, D͞C ଓ B͞C ର ମଧ୍ୟବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : MNPQ ଚତୁର୍ଭୁଜଟି ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।

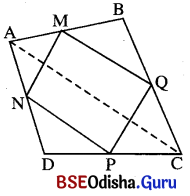
ଅଙ୍କନ : A͞C କଣ୍ଠ ଅଙ୍କନ କର ।
ପ୍ରମାଣ : Δ BAC ରେ M ଓ Q ଯଥାକ୍ରମେ A͞B ଓ B͞C ର ମଧ୍ୟବିନ୍ଦୁ ।
⇒ MQ || AC ଏବଂ MQ = \(\frac{1}{2}\) AC … (i)
ସେହିପରି Δ DAC ରେ N ଓ P ଯଥାକ୍ରମେ AD ଓ D͞C ର ମଧ୍ୟବିନ୍ଦୁ ।
⇒ NP || AC ଏବଂ NP = \(\frac{1}{2}\) AC … (ii)
∴ (i) ଓ (ii) ରୁ MQ || NP ଏବଂ MQ = NP
⇒ MNPQ ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । (ପ୍ରମାଣିତ)

Question 18.
ପ୍ରମାଣ କର ଯେ, ଆୟତଚିତ୍ରର ବାହୁମାନଙ୍କର ମଧ୍ୟବିନ୍ଦୁଗୁଡ଼ିକୁ ପର୍ଯ୍ୟାୟକ୍ରମେ ଯୋଗକଲେ, ଉତ୍ପନ୍ନ ଚତୁର୍ଭୁଜଟି ଏକ ରମ୍ବସ୍ ହେବ ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ଆୟତଚିତ୍ରରେ M, N, P ଓ Q ଯଥାକ୍ରମେ AB, AD, DC ଓ B͞C ର ମଧ୍ୟବିନ୍ଦୁ । MNPQ ଏକ ଚତୁର୍ଭୁଜ ।
ପ୍ରାମାଣ୍ୟ : MNPQ ଚତୁର୍ଭୁଜଟି ଏକ ରମ୍ବସ୍ ।

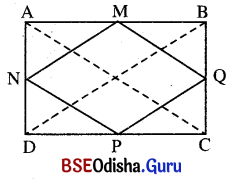
ଅଙ୍କନ : A͞C ଓ B͞D କର୍ଣ୍ଣଦ୍ଵୟ ଅଙ୍କନ କର ।
ପ୍ରମାଣ : ABCD ଅ‍।ୟତଚିତ୍ରରେ AC = BD ।
Δ ABD ରେ A͞B ର ମଧ୍ୟବିନ୍ଦୁ M ଓ AD ର ମଧ୍ୟବିନ୍ଦୁ N ।
⇒ MN = \(\frac{1}{2}\) BD … (i)
ସେହିପରି PQ = \(\frac{1}{2}\) BD … (i)
(i) ଓ (ii) ରୁ MN = PQ
ସେହିପରି MQ = \(\frac{1}{2}\) AC ଓ NP = \(\frac{1}{2}\) AC
⇒ MQ = NP
⇒ NP = MN (∵ AC = BD)
∴ M = NP = PQ = MQ ଅର୍ଥ।ତ୍ MNPQ ଏକ ରମ୍ବସ୍ । (ପ୍ରମାଣିତ)

Question 19.
ପ୍ରମାଣ କର ଯେ, ବର୍ଗଚିତ୍ରର ବାହୁମାନଙ୍କର ମଧ୍ୟବିନ୍ଦୁଗୁଡ଼ିକୁ ପର୍ଯ୍ୟାୟକ୍ରମେ ଯୋଗକଲେ, ଉତ୍ପନ୍ନ ଚତୁର୍ଭୁଜଟି ଏକ ବର୍ଗଚିତ୍ର ହେବ ।
ସମାଧାନ:
ଦତ୍ତ : ABCD ବର୍ଗଚିତ୍ରରେ M, N, P ଓ Q ଯଥାକ୍ରମେ AB, AD, DC ଓ BC ର ମଧ୍ୟବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : MNPO ଏକ ବର୍ଗଚିତ ।

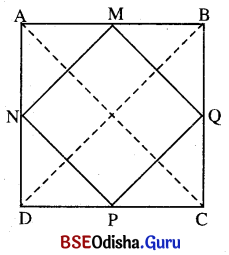
ଅଙ୍କନ : A͞C ଓ B͞D ଅଙ୍କନ କର ।
ପ୍ରମାଣ : 17 ନମ୍ବର ପ୍ରଶ୍ନର ସମାଧାନରୁ ପାଇବା MNPQ ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
କିନ୍ତୁ MQ = \(\frac{1}{2}\) AC ଏବଂ MN = \(\frac{1}{2}\) BD
⇒ MQ = MN (∵ AC = BD)
⇒ MNPQ ଏକ ରମ୍ବସ୍ ।
ପୁନଶ୍ଚ, Δ AMN ରେ AM = AN
(∵ AB = AD ⇒ \(\frac{1}{2}\) AB = \(\frac{1}{2}\) AD)
m∠A = 90° ହେତୁ m∠AMN = 45° । ସେହିପରି m∠BMQ = 45° ।
∴ m∠NMQ = 180° – (45° + 45°) = 90°
∴ MNPQ ରମ୍ବସ୍ ଏକ ବର୍ଗଚିତ୍ର । (ପ୍ରମାଣିତ)

Question 20.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ P ଓ Q ଯଥାକ୍ରମେ C͞D ଓ C͞B ର ମଧ୍ୟବିନ୍ଦୁ ଯଥାକ୍ରମେ PQ, AC କଣ୍ଠକୁ R ବିନ୍ଦୁରେ ଛେଦ କରୁଥିଲେ, ଦର୍ଶାଅ ଯେ 4CR = AC ।

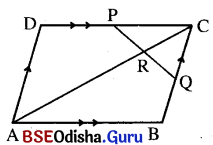
ସମାଧାନ:
ଦତ୍ତ : ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ P ଓ Q ଯଥାକ୍ରମେ D͞C ଓ BC ର ମଧ୍ୟବିନ୍ଦୁ । P͞Q ଓ A͞C ର ଛେଦବିନ୍ଦୁ R ।
ପ୍ରାମାଣ୍ୟ : CR = \(\frac{1}{4}\) AC
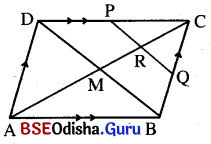
ଅଙ୍କନ : B͞D ଅଙ୍କନ କର । କଣ୍ଠଦ୍ଵୟର ଛେଦବିନ୍ଦୁ M ସ୍ଥିର କର ।
ପ୍ରମାଣ : CDB ରେ P ଓ Q
ଯଥାକ୍ରମେ C͞D ଓ C͞B ର ମଧ୍ୟବିନ୍ଦୁ ।
⇒ P͞Q || D͞B
Δ CDM ରେ P, C͞D ର ମଧ୍ୟବିନ୍ଦୁ ଏବଂ PR || DM (∵ PQ || DB)
⇒ R, C͞M ର ମଧ୍ୟବିନ୍ଦୁ ।
⇒ CR = \(\frac{1}{2}\) CM
⇒ CR = \(\frac{1}{2}\) (\(\frac{1}{2}\) AC) [∵ CM = AM]
⇒ CR = \(\frac{1}{4}\) AC 4CR = AC
(ପ୍ରମାଣିତ)