BSE Odisha 9th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(a)

Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(a)

Question 1.
ନିମ୍ନ ପ୍ରଶ୍ନମାନଙ୍କର ଉତ୍ତର ଦିଅ ।
(i) Δ ABC ର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ 12 ସେ.ମି., 5 ସେ.ମି. ଓ 13 ସେ.ମି., ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ବାହୁ ତ୍ରୟର ଦୈର୍ଘ୍ୟ a ସେ.ମି., b ସେ.ମି. ଓ c ସେ.ମି. ହେଲେ a = 12 ସେ.ମି., b = 5 ସେ.ମି. ଓ c = 13 ସେ.ମି. ।

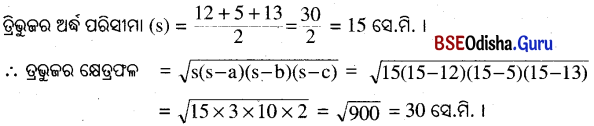
∴ Δ ABC ର ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ 30 ବର୍ଗ ସେ.ମି. ।

ବିକଳ୍ପ ପ୍ରଣାଳୀ :
ଏଠାରେ 12² + 5² = 13² । ତେଣୁ Δ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ।
Δ ABC ସମକୋଣୀ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × 12 × 5 = 30 ବର୍ଗ ସେ.ମି. ।

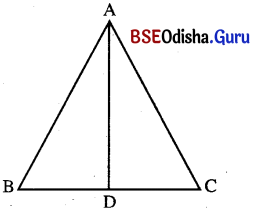
(ii) Δ ABC ରେ ଉଚ୍ଚତା AD = 12 ସେ.ମି. ଓ କ୍ଷେତ୍ରଫଳ = 96 ବର୍ଗ ସେ.ମି. । ଭୂମି BC କେତେ ?
ସମାଧାନ:
ABC ତ୍ରିଭୁଜର ଉଚ୍ଚତା (h) = AD = 12 ସେ.ମି. ଓ କ୍ଷେତ୍ରଫଳ = 96 ବର୍ଗ ସେ.ମି.
ମନେକର ତ୍ରିଭୁଜର ଭୂମି BC ର ଦୈର୍ଘ୍ୟ = b ସେ.ମି.
∴ Δ ABC ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) bh
= \(\frac{1}{2}\) × b × 12 = 6b ବର୍ଗ ସେ.ମି.
ପ୍ରଶ୍ବାନୁସାରେ, 6b = 96 ⇒ b = \(\frac{96}{6}\) = 16 ସେ.ମି.
∴ Δ ABC ର ଭୂମି BC ର ଦୈର୍ଘ୍ୟ 16 ସେ.ମି. ।

(iii) ABC ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ 25√3 ବର୍ଗ ଏକକ । ଏହାର ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ?
ସମାଧାନ:
ମନେକର ABC ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ = a ଏକକ
[∵ ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{\sqrt{3}}{4}\) × (ବାହୁ)²]

∴ ABC ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ 16 ସେ.ମି. । 

(iv) ABC ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ 25√3 ବର୍ଗ ସେ.ମି. ହେଲେ ଏହାର ଉଚ୍ଚତା କେତେ ?
ସମାଧାନ:
ମନେକର ABC ସମବାହୁ ତ୍ରିଭୁଜର ଉଚ୍ଚତା = h ଏକକ
[∵ ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ =  \(\frac{1}{\sqrt{3}}\) × (ଉଚ୍ଚତା)²]
ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ =  \(\frac{1}{\sqrt{3}}\) × h² ବର୍ଗ ସେ.ମି. ।
ପ୍ରଶ୍ବାନୁସାରେ, , ⇒ h² = 25 × 3
⇒ h = \(\sqrt{25 \times 3}\) = 5√3 ସେ.ମି. ।
∴ ସମବାହୁ ତ୍ରିଭୁଜର ଉଚ୍ଚତା 5√3 ସେ.ମି. ।

(v) ABC ସମବାହୁ ତ୍ରିଭୁଜର କୌଣସି ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁରୁ ବାହୁମାନଙ୍କ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବତ୍ରୟର ଦୈର୍ଘ୍ୟ 3 ସେ.ମି., 4 ସେ.ମି., ଓ 5 6ସେ.ମି., ହେଲେ ଏହାର ଉଚ୍ଚତା କେତେ ?
ସମାଧାନ:
ମନେକର ABC ସମବାହୁ ତ୍ରିଭୁଜରେ O, ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ I O͞P, O͞Q, O͞R ଯଥାକ୍ରମେ B͞C, A͞C ଓ A͞B ବାହୁ ପ୍ରତି ଲମ୍ବ ।
OP = 3 ସେ.ମି., OQ = 4 ସେ.ମି., ଏବଂ OR = 5 ସେ.ମି.
ମନେକର ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ = a ସେ.ମି.
O͞A, O͞B ଓ O͞C ଅଙ୍କନ କରାଯାଉ ।


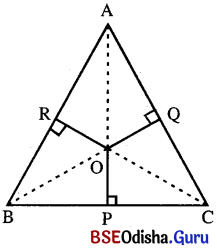
⇒ h = 12 ସେ.ମି.
∴ ତ୍ରିଭୁଜର ଉଚ୍ଚତା 12 ସେ.ମି. ।

ବିକଳ୍ପ ସମାଧାନ:
ସମବାହୁ ତ୍ରିଭୁଜର ଉଚ୍ଚତା = ତ୍ରିଭୁଜର ଅନ୍ତଃସ୍ଥ ଏକ ବିନ୍ଦୁରୁ ବାହୁମାନଙ୍କ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ ତ୍ରୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି 
= (3 + 4 + 5) ସେ.ମି. = 12 ସେ.ମି. ।

(vi) ଗୋଟିଏ ଆୟତକ୍ଷେତ୍ରରେ ଗୋଟିଏ ସରଳରେଖା ଅଙ୍କନ କରିବାରୁ ଏହା ଦୁଇଗୋଟି ବର୍ଗକ୍ଷେତ୍ରରେ ପରିଣତ ହେଲା । ଆୟତକ୍ଷେତ୍ରର ଦୁଇ ସନ୍ନିହିତ ବାହୁମାନଙ୍କ ଅନୁପାତ କେତେ ?
ସମାଧାନ:
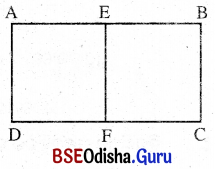
ABCD ଏକ ଅ‍।ୟତକ୍ଷେତ୍ର । E͞F ଅଙ୍କନ କରି ଦୁଇଟି ବର୍ଗଚିତ୍ର ADFE ଏବଂ EFCB ସୃଷ୍ଟି କରାଯାଇଛି ।
ଏଠାରେ AD = AE ଏବଂ BC = EB ।
ମନେକର ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = a ଏକକ ।
∴ AD = AE = EB = BC = a ଏକକ
∴ AB : AD = (a + a) : a = 2a : a = 2 : 1
∴ ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥର ଅନୁପାତ 2 : 1 ।

(vii) ଗୋଟିଏ ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥକୁ 3 ଗୁଣ କଲେ, ଲବ୍ଧ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ଦତ୍ତ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳର କେତେ ଗୁଣ ?
ସମାଧାନ:
ମନେକର ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ = a ଏକକ ଓ ପ୍ରସ୍ଥ = b ଏକକ .. କ୍ଷେତ୍ରଫଳ = ab ବର୍ଗ ଏକକ
ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ପ୍ରତ୍ୟେକ 3 ଗୁଣ ଲେଖାଏଁ ହୋଇଗଲେ ଦୈର୍ଘ୍ୟ = 3a ଏକକ ଓ ପ୍ରସ୍ଥ = 3b ଏକକ ହେବ । 
ସେତେବେଳେ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = 3a × 3b = 9ab ବର୍ଗ ଏକକ ହେବ ।
∴ ନୂତନ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ପ୍ରଥମ ଆୟତକ୍ଷେତ୍ରର = \(\frac{9 a b}{a b}\) = 9 ଗୁଣ ହେବ ।

(viii) ଗୋଟିଏ ଆୟତକ୍ଷେତ୍ରର ଗୋଟିଏ ବାହୁ 4 ମିଟର ଓ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 5 ମିଟର । କ୍ଷେତ୍ରଟିର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ଆୟତକ୍ଷେତ୍ରର ଗୋଟିଏ ବାହୁ = 4 ମି. ଓ କର୍ଣ୍ଣୟ ଦୈର୍ଘ୍ୟ = 5 ମି.
ଆୟତକ୍ଷେତ୍ରର ଅନ୍ୟ ବାହୁର ଦୈର୍ଘ୍ୟ = \(\sqrt{5^2-4^2}\) = \(\sqrt{25-16}\) = 3 ମି.
∴ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଦୈର୍ଘ୍ୟ × ପ୍ରସ୍ଥ = 4 × 3 ବ. ମି. = 12 ବ.ମି. 
∴ ଆୟତକ୍ଷେତ୍ରଫର କ୍ଷେତ୍ରଫଳ 12 ବର୍ଗ ମିଟର ।

(ix) ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ରର କଣ୍ଠର ଦୈର୍ଘ୍ୟ 4 ସେ.ମି. ହେଲେ ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ବର୍ଗକ୍ଷେତ୍ରର କଣ୍ଠର ଦୈର୍ଘ୍ୟ = 4 ସେ.ମି. ।
[∵ ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac{1}{\sqrt{2}}\) କଣ୍ଠର ଦୈର୍ଘ୍ୟ]
ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac{1}{\sqrt{2}}\) କଣ୍ଠର ଦୈର୍ଘ୍ୟ = \(\frac{4}{\sqrt{2}}\) = 2√2 ସେ.ମି. ।
∴ ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (ବାହୁର ଦୈର୍ଘ୍ୟ)² = (2√2)² = 8 ବର୍ଗ ସେ.ମି. ।

(x) ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ର ଓ ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ ସମାନ । ସେମାନଙ୍କ କ୍ଷେତ୍ରଫଳର ଅନୁପାତ କେତେ ?
ସମାଧାନ:
ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ର ଓ ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ ସମାନ ।
ମନେକର ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ = a ଏକକ ।
∴ ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (ବାହୁର ଦୈର୍ଘ୍ୟ)² = a² ବର୍ଗ ଏକକ ।

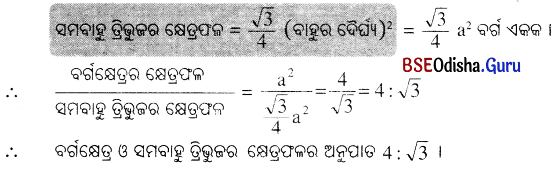
ବର୍ଗକ୍ଷେତ୍ର ଓ ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ 4 : √3 ।

(xi) ଏକ ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ 4 ସେ.ମି. ହେଲେ ସମକୋଣରୁ କର୍ଣ୍ଣ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ କେତେ ?
ସମାଧାନ:
Δ ABC ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ = AB = BC = 4 ସେ.ମି. ।
Δ ABC ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × (4 × 4) = 8 ବର୍ଗ ସେ.ମି.
Δ ABC ରେ B͞D ⊥ A͞C । ମନେକର BD ର ଦୈର୍ଘ୍ୟ = x ସେ.ମି. I
AC କର୍ପୂର ଦୈର୍ଘ୍ୟ = ସମାନ ବାହୁ × √2 = 4√2 ସେ.ମି. ।
A͞C କୁ ଭୂମି ଓ B͞D କୁ ଉଚ୍ଚତା ନେଲେ Δ ABC ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) AC . BD
= \(\frac{1}{2}\) × 4√2 × x ବର୍ଗ ସେ.ମି. = 2√2x ବର୍ଗ ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, 2√2x = 8
⇒ x = \(\frac{8}{2 \sqrt{2}}\) =2√2 ସେ.ମି. ।
∴ ସମକୋଣରୁ କର୍ଣ୍ଣପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ 2√2 ସେ.ମି. ।

Question 2.
ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ :
(i) ABCD ଆୟତକ୍ଷେତ୍ରର BC – AB = 20 ମିଟର ଓ AB : BC = 4 : 5 । ABCD ଆୟତକ୍ଷେତ୍ରର ପରିସୀମା କେତେ ?
ସମାଧାନ:
ABCD ଆୟତକ୍ଷେତ୍ରର BC – AB = 20 ମିଟର ଓ AB : BC = 4 : 5 । 
ମନେକର ABର ଦୈର୍ଘ୍ୟ = 4x ମି. ଓ BC ର ଦୈର୍ଘ୍ୟ = 5x ମି.
ପ୍ରଶ୍ନନୁସାରେ, 5x – 4x = 20 ⇒ x = 20 ମି.
∴ AB = 4x = 4 × 20 = 80 ମିଟର ଓ BC = 5x = 5 × 20= 100 ମିଟର
∴ ଆୟତକ୍ଷେତ୍ରର ପରିସୀମା = 2 (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ) = 2 (100 + 80) ମିଟର = 2 × 180 ମିଟର = 360 ମିଟର ।
∴ ABCD ଆୟତକ୍ଷେତ୍ରର ପରିସୀମା 360 ମିଟର ।

(ii) ABCD ବର୍ଗକ୍ଷେତ୍ରର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ 4 ସେ.ମି. ବୃଦ୍ଧିକଲେ କ୍ଷେତ୍ରଫଳରେ 60 ବର୍ଗ ସେ.ମି. ବୃଦ୍ଧି ହୁଏ । ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ?
ସମାଧାନ:
ମନେକର ABCD ବର୍ଗକ୍ଷେତ୍ରର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ = x ସେ.ମି. ।
ABCD ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (ବାହୁ) = x² ବର୍ଗ ସେ.ମି.
ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ 4 ସେ.ମି. ବୃଦ୍ଧିହେଲେ ବାହୁର ଦୈର୍ଘ୍ୟ ହେବ = (x + 4) ସେ.ମି.
ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (x + 4) ବ. ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, (x + 4)² = x² + 60
⇒ (x + 4)² – x² = 60
⇒ (x + 4 + x) (x + 4 – x) = 60
⇒ 2x + 4 = \(\frac{60}{4}\) =15 ⇒ 2x = 11
⇒ x = \(\frac{11}{2}\) = 5.5 ସେ.ମି.
ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ 5.5 ସେ.ମି. ।

(iii) ଗୋଟିଏ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ପରିସୀମା 18 ସେ.ମି. । ଭୂମି ଓ ଏକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟର ଅନୁପାତ 8 : 5 ହେଲେ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ ନିରୂପଣ କର ।
ସମାଧାନ:

ମନେକର ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ = 8x ସେ.ମି. 
ଓ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ = 5x ସେ.ମି.
ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ପରିସୀମା = 18 ସେ.ମି.
ପ୍ରଶ୍ବାନୁସାରେ, 8x + 5x + 5x = 18
⇒ 18x = 18 ⇒ x = \(\frac{18}{18}\) = 1 ସେ.ମି.
∴ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ = 8x = 8 ସେ.ମି. ଓ ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ = 5x = 5 ସେ.ମି.
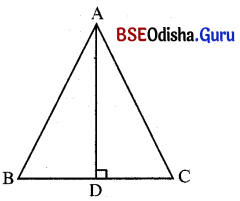
ABC ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ (BC) = 8 ସେ.ମି. ଓ ସମାନବାହୁର ଦୈର୍ଘ୍ୟ  AB = AC = 5 ସେ.ମି.
ଓ A͞D ⊥ B͞C ।

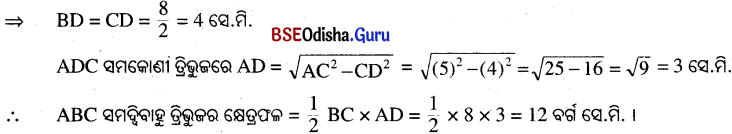
Question 3.
ଗୋଟିଏ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ଏକ ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳର ଅଧା । ଏହାର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟଠାରୁ 12 ମିଟର ବେଶୀ ଏବଂ ଅନ୍ୟ ବାହୁର ଦୈର୍ଘ୍ୟ 12 ମିଟର କମ୍ ହେଲେ, ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = a ମି., ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = a² ବ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ = (a + 12) ମି. ଓ ପ୍ରସ୍ଥ = (a – 12) ମି.
ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଦୈର୍ଘ୍ୟ x ପ୍ରସ୍ଥ (a + 12)(a – 12) ବ.ମି. = (a² – 144) ବ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, a – 144 = \(\frac{\mathrm{a}^2}{2}\)
⇒ 2a² – 288 = a² ⇒ a² = 288 ବ.ମି.
∴ ଆୟତକ୍ଷେତ୍ରର ପ୍ରଶାନୁସାରେ, a² – 144 = 288 – 144 = 144 ବ.ମି.

Question 4.
ଗୋଟିଏ ଘରର ଚାରିକାନ୍ଥର କ୍ଷେତ୍ରଫଳ 540 ବର୍ଗମିଟର ଏବଂ କାନ୍ଥର ଉଚ୍ଚତା 10 ମିଟର । ଘରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥର ଅନୁପାତ 5 : 4 ହେଲେ, ଚଟାଣର କ୍ଷେତ୍ରଫଳ ନିଶ୍ଚୟ କର ।
ସମାଧାନ:
ମନେକର ଘରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ଯଥାକ୍ରମେ 5x ମି. ଓ 4x ମି. । କାନ୍ଥର ଉଚ୍ଚତା = 10 ମି. ।
ଘରର ଚାରିକାନ୍ଥର କ୍ଷେତ୍ରଫଳ = 2 (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ) × ଉତ୍ତର = 2(5x + 4x) × 10 = 180x ବ.ମି.
ପ୍ରଶ୍ବାନୁସାରେ, 180x = 540
⇒ x = \(\frac{540}{180}\) = 3
ଘରର ଦୈର୍ଘ୍ୟ = 5x = 5 x 3 = 15 ମି. ଏବଂ ପ୍ରସ୍ଥ = 4x = 4 × 3 = 12 ମି.
ଚଟାଣର କ୍ଷେତ୍ରଫଳ = ଦୈର୍ଘ୍ୟ x ପ୍ରସ୍ଥ = 15 ମି. × 12 ମି. = 180 ବର୍ଗ ମି. 

Question 5.
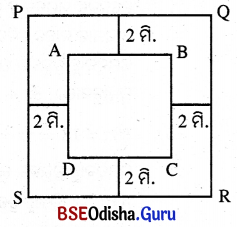
ଗୋଟିଏ ବର୍ଗାକାର ଜମିର ବାହାର ଧାରକୁ ଲାଗି 2 ମିଟର ଚଉଡ଼ାର ଏକ ରାସ୍ତା ଅଛି । ରାସ୍ତାର କ୍ଷେତ୍ରଫଳ 416 ବର୍ଗମିଟର ହେଲେ, ଜମିର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (ବାହୁର ଦୈର୍ଘ୍ୟ)²
ମନେକର ABCD ବର୍ଗାକାର ଜମିର ଦୈର୍ଘ୍ୟ =  AB = a ମି.
ଏହି କ୍ଷେତ୍ରର ବାହାର ଧାରକୁ ଲାଗି 2 ମି. ଚଉଡ଼ାର ଏକ ରାସ୍ତା ଅଛି । 
∴ ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = PQ
= a ମି. + 2 × 2 ମି. = (a + 4) ମି.
ABCD ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = a² ବର୍ଗ ମି.
PORS ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (a + 4)² ବର୍ଗ ମି.
PORS ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ – ABCD ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ରାସ୍ତାର କ୍ଷେତ୍ରଫଳ
⇒ (a + 4)² – a² = 416
⇒ a² + 8a + 16 – a² = 416
⇒ 8a + 16 = 416 ⇒ 8a = 400
⇒ a = \(\frac{400}{8}\) = 50
∴ ଜମିର କ୍ଷେତ୍ରଫଳ = a² = (50)² = 2500 ବର୍ଗମିଟର ।

Question 6.
ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ 44 ମିଟର ଏବଂ ଅନ୍ୟ ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି 88 ମିଟର ହେଲେ, ଏହାର କ୍ଷେତ୍ରଫଳ ନିଶ୍ଚୟ କର ।
ସମାଧାନ:
ମନେକର ସମକୋଣୀ ତ୍ରିଭୁଜର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = x ମି. । ପ୍ରଶ୍ନନୁସାରେ, ଲମ୍ବର ଦୈର୍ଘ୍ୟ = (88 – x) ମି. 
ସମକୋଣୀ ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ = 44 ମି.
ଅ‍।ମେ ଜାଶିଛେ h² = p² + b²
⇒ x² = (88 – x)² + (44)²
⇒ x² = 7744 + x² – 176x + 1936
⇒ 176x = 9680 ⇒ x = 55
ସମକୋଣୀ Δ ର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = (88 – x) ମି. = (88 – 55) ମି. = 33 ମି.
ସମକୋଣୀ Δ ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ଭୂମି × ଉଚ୍ଚତା = \(\frac{1}{2}\) × 44 × 33 = 726 ବର୍ଗ ମି.

Question 7.
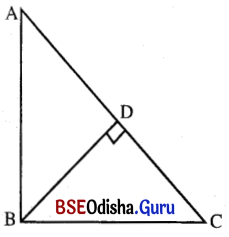
କୌଣସି ସମକୋଣୀ ତ୍ରିଭୁଜର ସମକୋଣ ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 45 ସେ.ମି. ଓ 60 ସେ.ମି. ହେଲେ ସମକୋଣରୁ କର୍ଣ୍ଣପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

Question 8.
ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ 2 ମିଟର ବଢ଼ାଇଦେଲେ ଏହାର କ୍ଷେତ୍ରଫଳ 6√3 ବର୍ଗମିଟର ବଢ଼ିଯାଏ । ଏହାର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

⇒ (a + 2)² = a² + 24 ⇒ a² + 4a + 4 = a² + 24
⇒ 4a = 20 ⇒ a = 5 ମି.

Question 9.
ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ 2 ସେ.ମି. କମାଇଦେଲେ ତାହାର କ୍ଷେତ୍ରଫଳ 16/3 ବର୍ଗସେ.ମି. କମିଯାଏ । ଏହାର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ  ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ସମବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ = a ସେ.ମି.

⇒ (a – 2)² = a² – 64
⇒ a² – 4a + 4 = a² – 64
⇒ 4a = 68
⇒ a = \(\frac{68}{4}\) = 17 ସେ.ମି.
∴ ସମବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ 17 ସେ.ମି.

Question 10.
ଗୋଟିଏ ସମକୋଣୀ ସମଙ୍ଗିବାହୁ ତ୍ରିଭୁଜର ସମକୋଣ ସଂଲଗ୍ନ ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 96 ସେ.ମି. ହେଲେ ଏହାର ସମକୋଣରୁ କର୍ଣ୍ଣପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ABC ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ସମାନ ବାହୁ AB = BC = 96 ସେ.ମି.

Question 11.
ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳର 3.5 ଗୁଣ । ବର୍ଗାକାର କ୍ଷେତ୍ରର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 20 ମିଟର ହେଲେ ତ୍ରିଭୁଜର ପରିସୀମା ନିଶ୍ଚୟ କର । ( √3 = 1\(\frac{3}{4}\))
ସମାଧାନ:
ବର୍ଗକ୍ଷେତ୍ରର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 20 ମି.

∴ ସମବାହୁ ତ୍ରିଭୁଜର ପରିସୀମା = 3a = 3 x 40 ମି. = 120 ମି. ।

Question 12.
ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜର ଅନ୍ତଃସ୍ଥ ଏକ ବିନ୍ଦୁରୁ ଏହାର ବାହୁମାନଙ୍କ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବତ୍ରୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 3 ସେ.ମି., 4 ସେ.ମି. ଓ 5 ସେ.ମି. ହେଲେ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ABC ସମବାହୁ Δ ରେ O ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ।

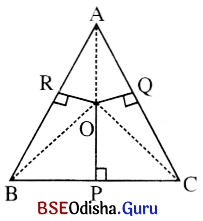
O͞P, O͞Q, O͞R ଯଥାକ୍ରମେ B͞C, A͞C ଓ A͞B ବାହୁ ପ୍ରତି ଲମ୍ବ ।
∴ OP = 3 ସେ.ମି., OQ = 4 ସେ.ମି. ଏବଂ OR = 5 ସେ.ମି. ।
ମନେକର ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ = a ସେ.ମି. ।
ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{\sqrt{3}}{4}\) a² ବର୍ଗସେ.ମି.
O͞A, O͞B ଓ O͞C ଅଙ୍କନ କରାଯାଉ ।

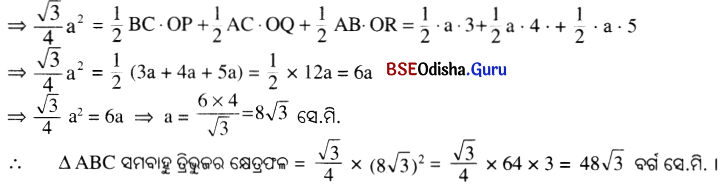
Question 13.
ଗୋଟିଏ ତ୍ରିଭୁଜର ପରିସୀମା 84 ସେ.ମି., ଏହାର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 30 ସେ.ମି. ଓ କ୍ଷେତ୍ରଫଳ 336 ବର୍ଗ ସେ.ମି. ହେଲେ ଅନ୍ୟ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
ତ୍ରିଭୁଜର ପରିସୀମା = 84 ସେ.ମି., ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ = 30 ସେ.ମି.
ଅନ୍ୟ ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି = (84 – 30) ସେ.ମି. = 54 ସେ.ମି. ।
ମନେକର, ଏଥୁମଧ୍ୟରୁ ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ x ସେ.ମି. । ତେଣୁ ଅନ୍ୟ ବାହୁଟିର ଦୈର୍ଘ୍ୟ (54 – x) ସେ.ମି ।

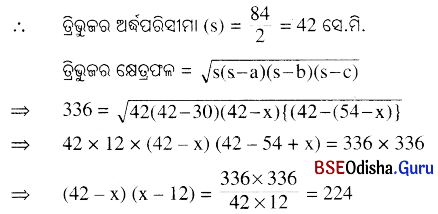
⇒ 42x – 504 – x² + 12x = 224
⇒ x² – 54x + 728 = 0
⇒ x² – 26x – 28x + 728 = 0
⇒ x (x – 26) – 28 (x – 26) = 0
⇒ (x – 26) (x – 28) = 0
⇒ x – 26 = 0 ବୀ x – 28 = 0
⇒ x = 26 ବୀ x = 28
x = 26 ସେ.ମି. ହେଲେ (54 – x) = 28 ସେ.ମି. ଏବଂ ଯଦି x = 28 ହେଲେ 54 – x = 26
∴ ତ୍ରିଭୁଜର ଅନ୍ୟ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 26 ସେ.ମି. ଓ 28 ସେ.ମି. ।

Question 14.
ଗୋଟିଏ ତ୍ରିଭୁଜର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 25 ସେ.ମି., 29 ସେ.ମି. ଓ 36 ସେ.ମି. ହେଲେ, ଏହାର ବୃହତ୍ତମ ବାହୁ ଉପରେ ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଗୋଟିଏ Δ ର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ a = 25 ସେ.ମି., b = 29 ସେ.ମି. ଓ c = 36 ସେ.ମି ।

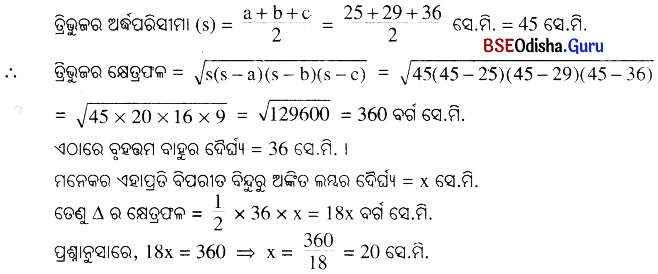
∴ ବୃହତ୍ତମ ବାହୁ ଉପରେ ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ 20 ସେ.ମି. ।

Question 15.
ଗୋଟିଏ ତ୍ରିଭୁଜର ବାହୁମାନଙ୍କ ଦୈର୍ଘ୍ୟର ଅନୁପାତ 3 : 5 : 7 ଓ ପରିସୀମା 300 ମିଟର ହେଲେ, ତ୍ରଭୁଜର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ତ୍ରିଭୁଜର ବାହୁମାନଙ୍କ ଦୈର୍ଘ୍ୟ 3x ମି., 5x ମି. ଓ 7x ମି. ।
ପରିସୀମା = 3x + 5x + 7x = 15x ମିଟର ।

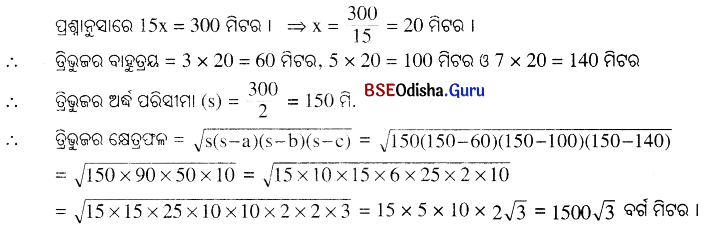
∴ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = 1500√3 ବର୍ଗ ମିଟର ।

Question 16.
ଗୋଟିଏ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ପରିସୀମା 30 ସେ.ମି. ଓ ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ 12 ସେ.ମି. ହେଲେ, ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

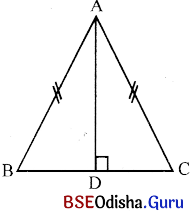
ABC ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ସମାନ ବାହୁ AB = BC = 12 ସେ.ମି.
∴ Δ ABC ର ପରିସୀମା = 30 ସେ.ମି.
∴ ଭୂମି (BC) ର ଦୈର୍ଘ୍ୟ = 30 – (2 × 12) = 30 – 24 = 6 ସେ.ମି. ।

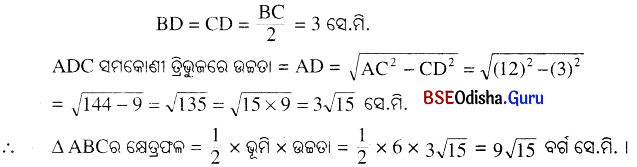
∴ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = 9√15 ବର୍ଗ ମିଟର ।